由APN幂函数构造上的置换

田诗竹

（1. 中国科学院信息工程研究所信息安全国家重点实验室，北京100093；2. 中国科学院大学，北京 100049）

田诗竹1,2

（1. 中国科学院信息工程研究所信息安全国家重点实验室，北京100093；2. 中国科学院大学，北京 100049）

APN函数是特征为2的有限域上达到最低差分均匀度的函数，其中最经典的是APN幂函数。在F22n上的APN幂函数都是3-1函数。推广了前人在奇特征有限域上由2-1函数构造置换的思想，得到偶特征域上由3-1函数构造置换的方法，并由F22n上的APN幂函数构造置换。根据这种构造，研究了此类置换的差分性质。

有限域；置换多项式；APN；幂函数

1 引言

有限域上的置换多项式广泛应用于密码学、编码理论和组合设计。一些分组密码的设计在多个环节需要利用有限域上的置换多项式（如AES的S盒是上的4差分置换多项式）。

设Fq是含q个元素的有限域，其中q是一个素数的次幂。若映射是由Fq到本身的置换，则称为Fq上的置换多项式。显然，f( x)为Fq上的置换多项式的充要条件是对于任意，方程 f( x)=a有唯一解[1]。近年来，置换多项式是国内外许多专家学者的研究热点。侯向东在文献[2]中总结了近年来国内外关于置换多项式的主要研究成果。

在分组密码的S盒设计中一般要求其具有抵抗差分攻击的能力，1993年，Nyberg在文献[3]中提出了差分均匀度的概念。差分均匀度反映了函数抵抗差分攻击的能力。

定义1Fq是含q个元素的有限域，f( x)是由Fq到自身的映射。则f( x)的差分均匀度为

1) Gold函数[5]： 2i1 d= + ，gcd(i, n)=1，

2) Kasami函数[6]：

5) Inverse函数： 2n2 d= - ，n为奇数。

6) Dobbertin 函数[7]：

文献[15]提出了将2-1的PN函数变为1-1函数的思想，构造了特征为奇数的有限域上的低差分置换多项式。借鉴了文献[15]的构造思想并将它推广到了一般的情况，由特征为偶数的有限域上的3-1的APN函数构造置换多项式。本文第2节给出由3-1函数构造置换的方法和证明。第3节研究具体由Gold函数得到的置换的差分性质，在较小域上，通过程序计算了由 Gold函数、Kasami函数以及Dobbertin函数构造的置换的差分均匀度。对于n较大的域上，给出了由Gold函数构造的置换的差分均匀度的上界。

2 构造置换

在文献[15]中，提出了由奇特征域上的 2-1函数构造置换的方法，并发现由PN型的2-1函数构造的这种置换，在某些情形下有较好的差分性质。其主要思想是分段函数，将有限域划分为平方元与非平方元并将重合分支分别对应到但实际应用一般都在特征为偶数的有限域上的置换，而在偶特征域下1=-1，直接使用其方法并不可行。本节给出了在偶特征域下由3-1构造置换的方法。

命题1若 ()df x=x是F2n上的APN函数，则对于任意有xd=1当且仅当x3=1，即当n为奇数时，gcd(,2nd -1)=1；当n为偶数时，则APN幂函数在n为奇数时是置换，n为偶数时是 3-1函数。

根据命题1的结论，只需讨论n为偶数的情况。 在接下来的讨论中设n是任意正整数，考虑在有限域上置换多项式的构造。

2.1 构造思路

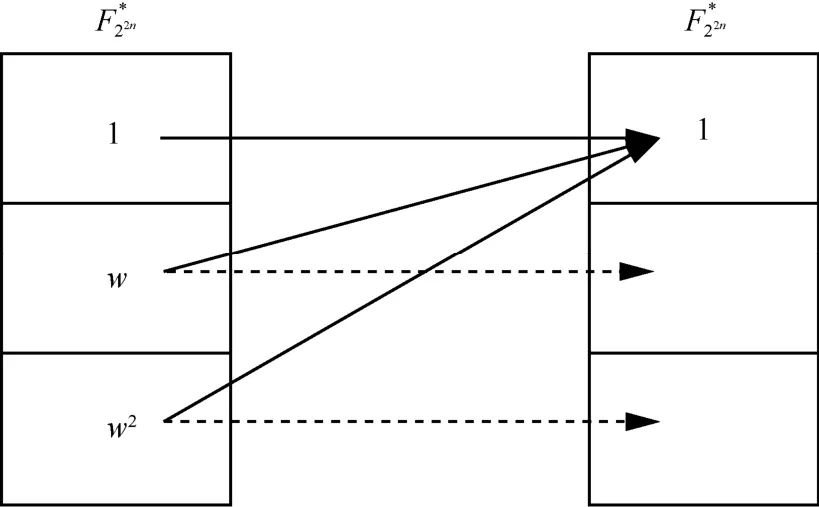
图1 构造思路图

下面给出有限域的2种划分，分别对应图1的左右2个域。

定义 2α是的本原元，w是三次本原单位根，定义

定义3α是的本原元，定义

显然，

2.2 构造及证明

设 ()df x=x是上的 APN幂函数，α是的本原元，如上面的定义，构造G( x)如下。

定理 1设是上的APN幂函数，α是的本原元，如上面的定义，式(1)给出了函数G( x)是上的置换。

证明首先，当且仅当x=0，只需考虑G( x)≠0的情况。假设存在使不妨设

注：通过上面的分析和证明可知这种构造可以做简单的拓展，将它推广为

3 差分性质

本节主要考查由 APN幂函数构造的置换的差分性质。在较小的域上（2n≤12）通过程序计算了这些函数的差分均匀度，并由表格给出。对于比较大的域，由于计算机计算能力的限制，从数学的角度给出了由 Gold函数构造的置换的差分均匀度的一个上界。

3.1 由Gold函数构造的置换

在文献[15]中，在奇特征域上通过对最优差分性质的2-1函数的改造，在某些条件下可以得到差分性质次优的置换。Gold函数在偶特征的有限域上是APN函数，当n为奇数时，其非线性度也达到最优。但当n为偶数且gcd(i, n)=1时，它不是置换。类似于文献[15]，希望通过第 2节中的方法将其改造为置换，同时差分性质并不改变很多。首先通过程序验证小域上的情形，发现对Gold型的这一改造对其差分性质有一定的影响。表 1给出具体域中此类函数差分均匀度的程序运行结果。

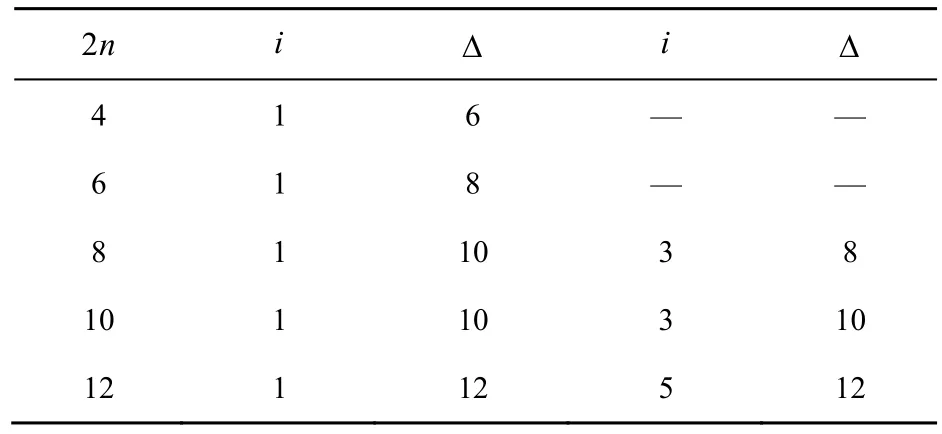
表1 由Gold函数构造的置换的差分均匀度

观察表 1，改造后的函数在具体域上的差分性质跟域的大小显示出一定的关系。目前，实际应用都在较小的域中使用。在上改造后的函数差分均匀度最优可以达到8，对比实际AES的S盒是上差分均匀度为4的置换，此改造后得到的置换有一定抵抗差分攻击的能力。但随着n的增大，其差分均匀度有上升的趋势，下面为了研究n足够大时其差分扩大的程度，在数学的角度给出了一个上界。

研究函数差分性质时主要需要分析有限域上一些方程的解数，以下文献[10]中的结论对后面的分析有重要作用。

命题2设F是有限域，对于记Ni为使方程有i个解的的个数。若是偶数，则

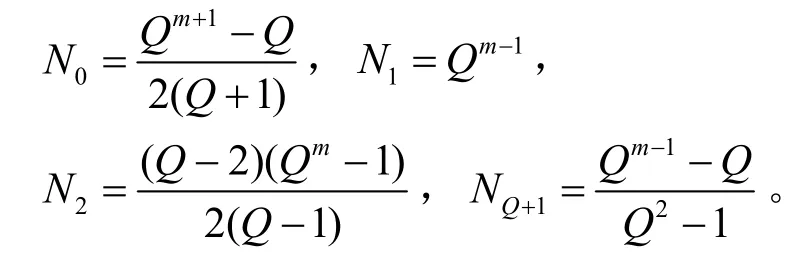
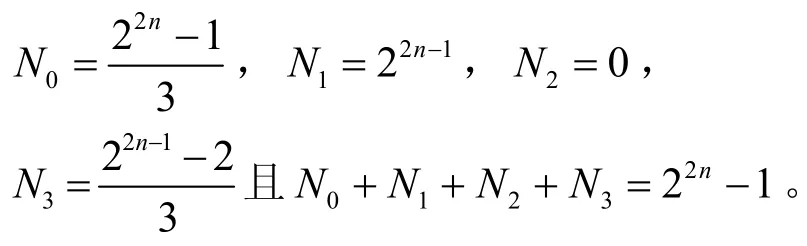
推论1则方程在上至多有3个解。实际上，它或者无解或者有一个解或者有3个解。

考虑方程

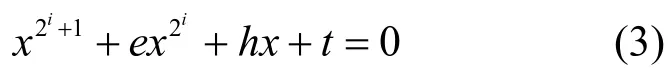
推论2方程在上至多有3个解。

下面给出 Gold函数构造的置换的差分均匀度的一个上界。

命题3是的本原元，如上面的定义，式(1)给出了函数G( x)在上的差分均匀度

证明固定任意考虑方程在上的解。首先，考虑的情形，对x进行划分。

由命题3和以上的分析知，由Gold函数构造的置换在较小域上的差分性质较优但达不到 4，随n增大，在较大域上的差分最大不会超过26。

3.2 由Kasami和Dobbertin函数构造的置换

由引言知，已知的APN幂函数满足构造要求的仅剩Kasami和Dobbertin（部分满足条件的n）。同样，本文通过程序验证其在较小域上的差分性质。表2给出具体域上其差分均匀度的结果。

观察表2，由Kasami和Dobbertin函数构造的置换在较小域上有较优的差分性质。在小域上的结果显示，改造后的函数差分达不到 4。对于较大的n，由于计算能力限制无法给出具体的差分，直接从数学的角度研究涉及更复杂的方程在有限域上的解数，有较大的难度。

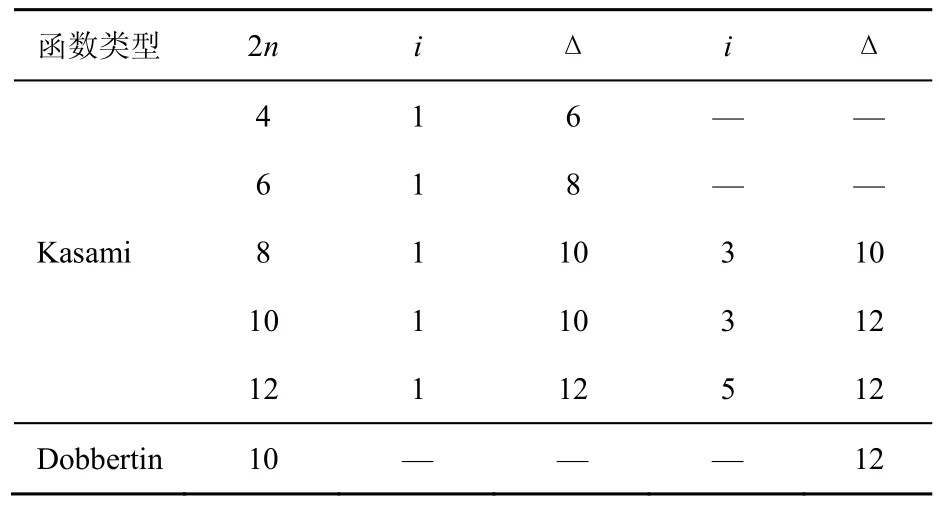
表2 由Kasami和Dobbertin函数构造的置换的差分均匀度

综上分析，由第2节中的方法构造的置换都在一定程度上改变了原函数的差分性质。通过程序实验结果未能得到4差分的置换，笔者猜想一般的情况下这种构造得到的置换都得不到4差分置换。但这类置换仍保有较优的差分，但从应用的角度，在较小域上的差分均匀度的结果有一定的密码学意义。

4 结束语

置换多项式在密码学和编码理论中有重要应用，本文主要将奇特征域上2-1函数构造置换的方法推广到了偶特征域上。利用APN幂函数构造了新的置换多项式，结合实验和理论分析了所得置换的差分性质。不同于原奇特征域上的情形，猜想在偶数的情形下通过此类方法得到的置换不具备次优的差分性质（4差分）。本文在应用的范围内，给出了此构造得到的置换的差分均匀度的具体值。这类置换差分性质更精细的刻画有待进一步研究。

[1] LIDL R, NIEDERREITER H. Finite fields[M]. Massachusetts:Addison-Wesley Publishing Company, 1983.

[2] HOU X D. Determination of a type of permutation trinomials over finite fields[J]. Finite Fields and Their Applications, 2015(35): 16-35.

[3] NYBERG K. Differentially uniform mappings for cryptography[C]//The Workshop on the Theory and Application of of Cryptographic Techniques. 1993:55-64.

[4] CARLET C. Vectorial boolean functions for cryptography[M].Cambridge: Cambridge University Press, 2010.

[5] GOLD R. Maximal recursive sequences with 3-value recursive crosscorrelation functions[J]. IEEE Trans Inform Theory, 1968(14):154-156.

[6] KASAMI T. The weight enumerators for several classes of subcodes of the second order binary Reed-Muller codes[J]. Information and Control, 1971(18): 369-394.

[7] DOBBERTIN H. Almost perfect nonlinear power functions on GF(2n): a new case for n divisible by 5[J]. Proceedings of Finite Fields and Applications Fq5. 2000:113-121.

[8] BROWNING K, DILLON J, MCQUISTAN M, et al. An APN permutation in dimension six[J]. Contemporary Mathematics.2010(58): 33-42.

[9] QU L J, TAN Y, TAN C, et al. Constructing differentially 4-uniform permutations overvia theswitching method[J]. IEEE Trans Inf Theory, 2013, 59(7): 4675-4686.

[10] LI Y Q, WANG M S. Constructing differentially 4-uniform permutations over GF(2n) from quadraticAPN permutations over GF(22n+1)[J]. Designs Codes amp; Cryptography, 2014, 61(6):249-264.

[11] TANG D, CARLET C, TANG X H. Differentially 4-uniform bijections by permuting the inverse function[J]. Designs Codes amp; Cryptography, 2015, 77(1): 117-141.

[12] PERRIN L, UDOVENKO A, BIRYUKOV A. Cryptanalysis of a theorem: Decomposing the only known solution to the big APN problem[C]//The 36th Annual International Cryptology Conference.2016:93-122.

[13] CANTEAUT A, DUVAL S, PERRIN L. A generalisation of Dillon’s APN permutation with the best known differential and nonlinear propertiesfor all fields of size 24k+2[J]. IEEE Transactions on Information Theory, 2016, (99):1-1.

[14] FU S H, FENG X T. Further results of the cryptographic properties onthe butterfly structure[J]. Computer Science—Information Theory, 2016(7)

[15] JIA W J, ZENG X Y, LI C L, et al. Permutation polynomials with low differential uniformity over finite fields of odd charateristic[J].Science China Mathematics, 2013(56): 1429-1440.

[16] BLUHER A B. On xq+1+ax+b[J]. Finite Fields and their Applications, 2004(10): 285-305.

Permutations from APN power functions over

TIAN Shi-zhu1,2

(1. The State Key Lab of Information Security, Institute of Information Engineering, Chinese Academy of Science, Beijing 100093, China;2. University of Chinese Academy of Sciences, Beijing 100049, China)

APN functions have the lowest differential uniform over finite fields with characteristic 2 and the APN power functions are the most classical ones. APN power functions are all 3-1 functions over F22n. By generalizing the idea of changing 2-1 functions to 1-1 functions over finite fields with odd characteristics, methods to change 3-1 functions over finite fields with even characteristics into permutations were obtained and permutations from APN power functions over F22n were constructed. According to the construction, the differential properties of permutations obtained by this method were discussed.

finite fields, permutation polynomials, APN, power functions

The National Natural Science Foundation of China (No.61379142)

TP393

A

10.11959/j.issn.2096-109x.2017.00203

2017-06-06；

2017-09-10。

田诗竹，tianshizhu@iie.ac.cn

国家自然科学基金资助项目（No.61379142）

田诗竹（1991-），女，湖北黄冈人，中国科学院信息工程研究所博士生，主要研究方向为信息安全、密码学。