基于多重分形理论的心电诊断系统设计与应用

张春慨，尹奥，张景旺，田攀博，周颖，齐常青

（哈尔滨工业大学（深圳）计算机科学与技术学院，广东 深圳 518055）

基于多重分形理论的心电诊断系统设计与应用

张春慨，尹奥，张景旺，田攀博，周颖，齐常青

（哈尔滨工业大学（深圳）计算机科学与技术学院，广东 深圳 518055）

设计实现了一种利用差分阈值法进行心电数据自动分段算法，该算法可识别连续心电数据的各个心电周期；基于多重分形理论，获取心电数据的多重分形半谱特征和广义Hurst指数特征，用于神经网络模型的训练，以实现心电数据分类，其分类的准确率为97%。实现了心电诊断系统并用于实际应用，该系统能自动识别包含多个周期的心电序列，忽略该心电序列中首尾不完整心电周期数据，并可对心电数据各个周期进行分类标注。

MFDFA；无标度区间；多重分形；神经网络

1 引言

目前，心电信号自动分类的研究侧重于时域和频域分析方法，但时频域分析仅能够从心电信号表面给出所测试数据的时域频域特征。心脏是一个复杂的非线性混沌系统，描述心脏活动的心电图具有混沌特性[1,2]，但目前混沌理论的研究与发展程度不足以对各种心电异常进行定量分析。分形作为非线性混沌系统中的一个重要研究内容，正逐步用来解决混沌系统的问题，已有研究人员证明了心电信号具有多重分形特性[3,4]，并利用心电信号的多重分形特性来研究心电信号特征。

在分形数据分析研究不断发展中，人们发现单重分形存在一个明显的短板，即它只能度量数据的整体分形特征，并不能完整地描述时间序列的非线性特征，缺乏对序列数据局部细节信息的描述。所以学者逐渐提出了多重分形数据分析的方法。Barabasi等[5]提出标准分割函数多重分形体系（standard partition function multifractal formalism）。但是该方法仍存在明显的不足，该方法对非平稳、非正规且带有趋势影响的时间序列分析能力有限。Kantelhardt等[6]对 DFA（detrended fluctuation analysis）方法进行推广并扩展得到多重分形去趋势波动分析（MFDFA, multifractal DFA）方法。MFDFA不仅拥有易于使用、便于理解、计算量小、运行速度快等优点，而且对带有趋势的不平稳时间序列的多重分形分析有较好的适用性。由于MFDFA操作不复杂、运行时间短、算法成熟等优点，该方法已经在很多领域有所应用，如脑波分析[7]、物价变化[8]、网络流量分析[9]等。

心电信号自动分类研究的主要方向是对心电信号中各个特征波形及其波形特征参数的提取，以此来分析并诊断心电信号的类型。例如，时域分析[10]、形态学分析[11]、模糊神经网络[12]和小波分析[13,14]等方法已经被很多学者应用到 QRS波群的定位和分析工作中。其中，Pan等[15]提出了一种削弱由于基线漂移和高频噪声引起的信号混乱问题的方法，该方法首先对信号进行差分操作，并将经过差分处理之后的信号分别进行平方操作和滑动窗口积分处理，只有当平方数据和积分数据同时满足一定的预设值，一段QRS波群才可被监测。

2 基础理论

2.1 分形概念

定义如果一个集合A满足式(1)，则称集合A为分形集。其中

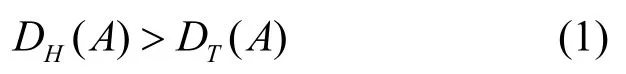
为集合A的哈茨沃弗维数，DT(A)为集合A几何维数。

采用式(1)的定义进行分形判断虽然正确，但仍然有部分的分形几何体会被遗漏，它不能包含一些有用的分形几何体。更加通俗易懂的定义为：几何或数据在对比整体与细节时，细节会以某一种形式与整体相似。具有上述性质的几何体或数据，称它们具有分形的特点。

经过学者不断地理论研究与实际应用，产生了多种观点以解释分形概念，增进对其的理解[16～18]，如下。

1) 结构非常细致，在很小的细节方面，局部蕴含整体的全部信息。

2) 分形其实是一种特性，并不局限于几何图形，也可能是由“功能”或“信号”组成具有分形特性的某种模型。

2.2 分形特性

分形最主要的2个性质是自相似性和无标度性。

1) 自相似性

分形理论中最具有代表性的特点之一就是自相似性，正如分形概念中提及的分形定义所描述的那样，判断事物是否具有分形特性的依据是事物是否具有自相似性。自相似性指事物的结构特征或过程特征在不同的观测尺度下，局部和整体表现一致或相似。

2) 无标度性

在分形几何体上任选一部分，将选取的局部区域进行放大变换，经放大变换后得到局部区域与原事物进行比较，发现原事物与经放大变换后得到的局部区域在形态特性方面表现相似或一致，这种特性称为无标度性。无标度区间是判断事物是否具有分形性的充分不必要条件。

2.3 分形维数

描述几何体形体特征的重要方式之一是维数，它表明了几何体自身对空间的填充能力。在研究和学习欧氏几何的过程中，所接触到的研究对象的形态都是理想的、规则的，即研究对象的维数都是非零的自然数。但如果要分析不规则的、复杂的几何体，传统分析方法的适用性就变得有限了。因此，从分形理论的角度看，正实数维数才是几何体正确有效的维数，整数只是其中的特殊实例。如果要正确地描述一个几何体的空间填充能力，就必须在恰当维数空间中对其进行描述。例如，如何获得某一个平面区域的分形维数？假设这个平面区域X包含边长为ε的正方形的个数为N()ε，该区域X的面为P，则可以得到

由此，可以得到X的维数为

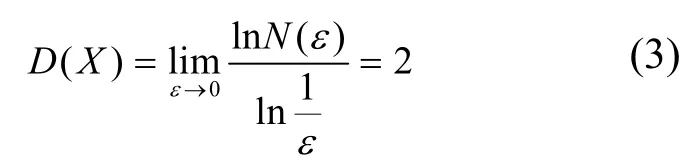
2.4 多重分形数据分析

单重分形分析仅能对时间序列数据的全局特征进行描述，缺乏对数据局部特征更细腻的刻画[19]，而多重分形分析作为单重分形分析的拓展，可以有效地处理这类现象，并被广泛用于对时间序列特征的刻画。

多重分形数据分析主要采用MFDFA方法进行处理，MFDFA方法过程如下。

2) 计算累计偏差序列Yi。

3) 计算局部均方根F( s, v)。

将累计偏差序列等分为Ns段，每段长s（也就是每段包含s点），最后段长为Tmods；再将累计偏差序列Yi从反向开始等分为Ns段，每段长s，最后段长为Tmods。这样共分为2Ns段，计算每一段的局部均方根，得到均方根序列f( s, v)。

5) 根据式(6)，以不同的q值进行分组，在组内取不同的s值对应得到多个F2(q; s)，利用式(7)过一元线性回归得到与q值对应的H值，最终获得多对(q, H)。

如果x( t)是具有多重分形性质的数据，H与q不是常数相关的；如果数据x( t)是单重分形性的时间序列，H与q是常数相关。

6) 计算质量指数τ(q)。

7) 计算奇异指数α。

其中，H′( q)如式(10)所示。

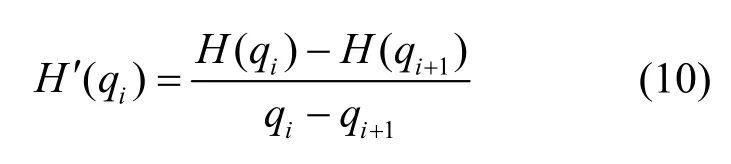
8) 计算奇异波谱f()α。

3 心电数据的特征分析

3.1 多重分形分析

从MIT心率异常数据库中，选取5条具有完整心电周期的心电数据。选取过程中保证这5条ECG（electrocardiograph）分别取自不同的类别，分别是正常心跳（NB, normal beat）、左束支传导阻滞心跳（LB, left bundle branch block beat）、右束支传导阻滞心跳（RB, right bundle branch block beat）、室性早搏心跳（PB, premature ventricular contraction）和房性早搏心跳（AB, atrial premature beat），并且是随机选取。如图1所示，对每一个类别进行随机抽取，总体是包含所有该类别的数据。

图1 5种心电信号

分别对提取的 5条心电时间序列应用MFDFA方法得到与之相对应的广义Hurst指数分布，如图 2所示，由多重分形方法可知广义Hurst指数 Hq与q的关系可以作为判断事物是否具有多重分形性的主要依据。由图 2可以看出这5条心电时间序列的广义Hurst指数Hq和q存在明显的递减关系。所以，可以得出结论，心电信号是具有多重分形性质的。在q和Hq变化过程中，在q的绝对值大于5之后，广义Hurst指数Hq的变化速度明显会变缓；在q的绝对值小于 5的情况下，心电信号的多重分形性质是最明显的。

图2 5种广义Hurst指数

在证明心电信号具有多重分形性质的实验基础上，本文进行了进一步的实验。在MIT-BIT数据库中对这5种心电数据分别随机抽取50个样本，对这一共250条心电信号应用MFDFA方法，提取其中 Hurst变化情况，如表 1所示。从表 1中可以看出，NB信号和RB信号之间的广义Hurst指数差距较小，NB信号、LB信号、RB信号、AB信号与PB信号差距较大。所以，广义Hurst指数的变换情况不能作为这5种心电信号的主要分类特征，它只能起到辅助心电信号分类的效果，如能区分某一信号是NB信号、LB信号、RB信号、AB信号中的一个还是PB信号，可以用来区分PB信号和AB信号。

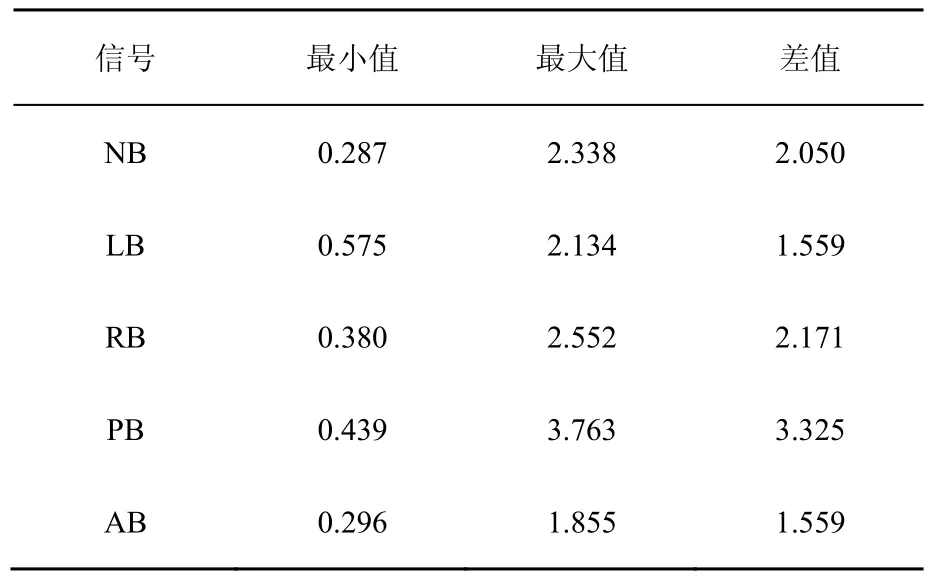
表1 5种广义Hurst指数变化

3.2 无标度区间分析

由前文的分形特性可知，具有分形特性的事物都具有无标度特性，即具有分形特性的事物都是在一个固定的无标度区间下才能表现出分形的特征，超出这一区间后，分形性就会被削弱甚至不具有分形特征。所以，在对心电信号进行处理时，无标度区间的确定是不可以忽略的。

同样，使用图3所示的5种信号无标度区间中的数据作为无标度区间的研究样本。对每一个样本数据应用 MFDFA方法进行处理，标度s预设在30～110，阶数q预设取值范围为-10,-5, -3, -1, 0, 1, 3, 5, 10。经过MFDFA方法处理，得到的实验结果如图 3所示。从实验结果可以看出，在q＞0且s在60～100之间时，ln Fq(s)与s呈现明显的线性关系，即60～100为其无标度区间。

3.3 心电数据的特征辨识

3.2节得到的无标度区间存在明显的问题：当q＞0时，所得到的多重分形性波谱并不是完整的多重分形波谱，而是其半谱，如图4所示。一般的多重分形波谱是一种具有单峰的曲线，即多重分形波谱具有一定的对称性。所以，本文假设心电信号的多重分形半谱可以作为心电信号的特征使用。

图3 5种信号无标度区间分析

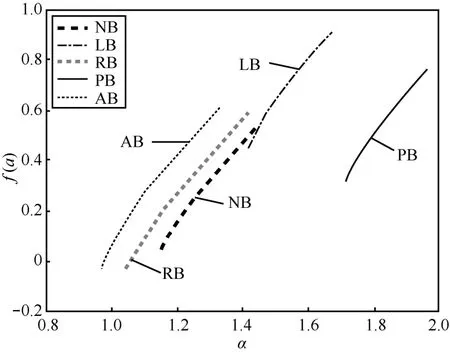
图4 5种信号的多重分形半谱

二项式乘法级联[20]（BMC, binomial multiplicative cascades）信号是一种典型的多重分形信号，如图5所示。从图5中可以明显看出，BMC信号是具有自相似性的，而它的产生完全是按照2.4节中的公式计算得到，可以说BMC信号是一种具有严谨多重分形性质的信号，即 BMC信号的无标度区间是无穷的。

图5 BMC信号

对BMC信号应用MFDFA方法，获得其多重分形波谱，如图6所示。从多重分形波谱中可以看出，BMC信号多重分形波谱是对称的，是可以用半谱表示全谱的，但是由MFDFA方法得出的多重分形波谱对称性稍弱。虽然如此，仍然可以得出结论，多重分形半谱可以近似地代表多重分形全谱。

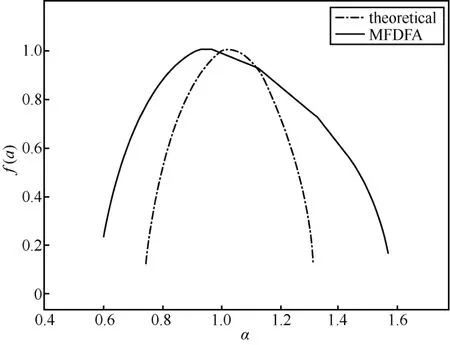
图6 BMC信号多重分形波谱

3.4 心电神经网络分类

本文采用前馈神经网络模型对心电信号进行识别分类，利用反向传播算法进行网络的权值调节以及阈值的调整。由于 BP网络模型在训练过程中涉及的参数比较多，所以必须不断地通过调节参数进行模型训练，并使用模型对心电信号标注的分类准确率判断模型的性能。

3.4.1 特征数量与分类结果

对5种心电信号应用MFDFA方法，获取其多重分形半波谱和广义 Hurst指数。对多重分形半波谱和广义Hurst指数提取特征，共分为4种特征列表。

1) 基本波谱特征

通常在使用多重分形波谱于分类特征时，研究者普遍使用式(12)作为特征向量。

其中，αmin为经过 MFDFA方法获得的多重分形半波谱中奇异值α的最小值，αmax为奇异值α的最大值，Δα为奇异值α的极值，fmin()α为波谱值f()α的最小值，fmax()α为波谱值f()α的最大值，Δf()α为波谱值f()α的极值。

2) 基本波谱特征和其拓展特征

这种情况除了包含式(12)中的6个特征值外，还有4个拓展特征。这4个拓展特征分别是：、和，如式(13)所示。其中，为经过MFDFA方法处理后获得的α序列的平均值，std()α为序列α的标准差，为经过MFDFA方法处理后获得的f(α)序列的平均值，而std( f(α))为序列f(α)的标准差。所以这种情况下的特征值如式(14)所示。

3) 基本波谱和广义Hurst指数特征

这种情况除了包含式(12)中的6个基本特征值之外，还包含3个广义Hurst指数特征。这3个广义Hurst指数特征分别为hmin、hmax和Δh，如式(15)所示。其中，hmin为经过 MFDFA方法处理后获得的广义 Hurst指数序列的最小值，hmax为广义Hurst指数序列的最大值，Δh为hmin与hmax的差值。所以这种列表包含的特征值如式(16)所示，即为式(12)和式(15)的并集。

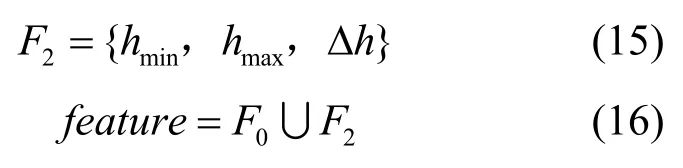
4) 基本波谱、波谱拓展和Hurst指数特征

在这种情况下，将前3种列表全部包含在内，其中不仅含有基本波谱特征，还有基本特征的拓展特征和广义Hurst指数特征，如式(17)所示。

将以上4种列表应用到前文已经构建好的网络模型中，对于每种列表分别进行训练测试 30次，取其迭代次数的平均值、准确度的平均值和准确度的标准差作为衡量标准，实验结果如表 2所示。

表2 特征数目与分类结果

从表2中可以看出，特征数目的增多会促进准确度的升高，但同时也增加了训练的时间消耗。训练时间与特征的数目是典型的正相关，但特征个数和迭代次数并不是明显的线性关系。从第1种列表到第2种列表准确度增长情况要比从第1种列表到第3种列表准确度增长更具有优势；将从第2种列表到第4种列表与从第3种列表到第4种列表进行对比发现，多重分形半谱的拓展特征对于网络模型的分类效果提升比广义Hurst指数好。而且，对比第1种列表与第3种列表，添加广义Hurst指数特征虽然会提高网络模型的分类效果，但同时会极大地增加网络模型的不稳定性；对比第2种列表和第4种列表，也会发现类似的情况。所以，广义 Hurst指数特征虽然对分类效果有一定的提升，但同时也会增加模型的不稳定性。

3.4.2 隐藏层与分类结果

将隐藏层神经元个数分别设为10、20、30和40，并分别用该神经网络模型对数据进行学习和验证。在隐藏层神经元数目确定的条件下，进行 30次训练与测试，取其迭代次数的平均值、准确度的平均值和准确度的标准差作为衡量标准。

从表3中可以看出，隐藏层神经元数目与迭代次数会呈现典型的正相关，但隐藏层神经元数目与迭代次数却是非线性的关系。

表3 隐藏层与迭代关系

从表4可以看出，随着隐藏层神经元数目的增加，模型的准确度会有所增加。但是，当隐藏层神经元数目超过30之后，准确度的增加会明显下降，甚至在第4种列表下准确度并没有提升而是有一定下降的趋势。将第2种列表和第1种列表与第3种列表和第1种列表进行对比发现，广义 Hurst指数对模型准确度的提升不如拓展多重分形半谱特征，但是将上述2种情况进行组合，即第4种情况时，准确度会有显著的提升。

表4 隐藏层与准确度关系

从表5中可以看到，随着隐藏层神经元个数的增加，模型对数据的预测的稳定性会增强。但是当隐藏层神经元个数达到30之后，稳定性减少变缓。

表5 隐藏层与准确度标准差

4 心电诊断系统构建

该系统主要流程：数据采集、数据初步分析、数据存储，如图7所示。

数据采集：主要通过医用心电图机进行数据采集；通过便携的心电图进行数据采集。

数据初步分析：去噪处理、自动分段、特征提取、模型分类数据标注。

数据处理：将经过初步分析得到的数据存储到本地数据库中或远程的服务器。

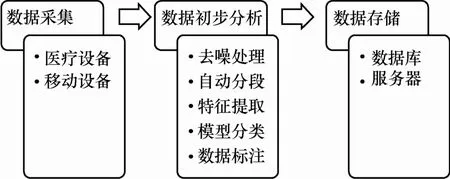
图7 系统结构

ECG数据分析的流程如图8所示。

图8 数据初步分析流程

1) 去噪处理

该过程主要进行低频噪声滤出、高频噪声滤出和心电周期的自动分段。

① 低频噪声滤出

低频噪声中的主要成分是基线漂移干扰，所以在滤除低频噪声时，使用的方法为小波变换强制滤除噪声方法。首先利用db5小波对心电信号进行分解，在分解的过程中将数据中的噪声信号（低频噪声）利用一维小波系数阈值方法进行滤除操作。

② 高频噪声滤出

高频噪声主要包含肌电干扰噪声和工频干扰噪声2部分，所以在滤除高频噪声时，使用方法为阈值门限滤波方法，同样使用db5小波进行多分辨率分解。

2) 自动分段

利用差分阈值法快速定位R波位置，然后在R波的位置分别向前、向后进行搜索一定的距离，分别为a、b。如果该R波在向前取信号的时候不能满足该固定长度a，即所能取得的最长信号小于a，就抛弃该R波所在的分段。同样地，如果该R波在向后取信号的时候不能满足该固定长度b，即所能取得的最长信号小于b，就抛弃该R波所在的分段。最终获得该段心电序列的各个心电周期分段，记录R波位置，并用R波位置区分各个心电周期信号。

3) 特征提取

对已经经过预处理的心电信号应用 MFDFA方法，提取该心电信号的多重分形半谱特征和广义Hurst指数特征，即式(17)，并将该特征向量作为神经网络分类模型的输出向量。

4) 模型分类

分类模型采用一个三层的前馈神经网络，并利用反向传播算法对各个神经元的权值和阈值进行更新。利用训练数据与测试数据对这个前馈神经网络模型进行多次训练，选取其中一个准确率在 97.5%左右的模型作为本文心电诊断系统的分类模型。与两篇近期的心电诊断论文[21,22]进行对比。文献[21]利用小波分析提取心电各个波形的特征作为心电信号的特征，并利用改进的BP神经网络算法进行训练，该模型的平均识别准确率达92.8%。文献[22]利用心电信号混沌特性分析与Lyapuov指数等作为心电信号的特征，并用BP神经网络进行分类，该模型的平均识别准确率达94.53%。将小波模型和混沌模型与本文的分形模型进行对比。对比结果如表 6所示。可见分形模型比小波模型的分类效果要好，尤其在PB信号的分类情况下提升效果非常明显。分形模型虽然对LB信号的识别能力稍微次于混沌模型，但是分形模型在对NB、RB、PB和AB信号的识别上，都明显高于混沌模型，尤其是对PB信号的识别。

5) 数据标注

通过模型分类之后，生成相应的数据标注文件。数据标注文件中内容为一个n×2的矩阵，n为该段心电信号的完整心电周期数目，第一列数据表示R波的位置，第二列数据表示该R波所在心电周期的心电信号的类别，其取值分别为N、L、R、P和A，分别代表NB信号、LB信号、RB信号、PB信号和AB信号。然后根据相应的数据标注文件生成相应的图或表。

表6 模型准确率对比分析

本文的主要研究内容是 NB、LB、RB、PB和AB信号，而且现实中只有这5种信号组成的ECG片段比较少，所以本文中所提到的ECG片段均由心电图模拟器仿真生成。将不同类型的心电信号排列成一个序列，并将该序列输入心电图模拟器中，最终生成一段 ECG片段。生成 100个由NB、LB、RB、PB和AB信号随机排列组成的ECG片段，每段ECG片段包含的周期数大约5～10。表7中TP表示正例被判断为正例的数目；FP为负例被判断为正例的数目；FN为正例被判断为负例的数目；TN为负例被判断为负例的数目。F1由式(18)计算获得。

其中，精确率(P)和召回率(R)分别由式(19)和式(20)计算得。

由表7可得，该系统对心电信号的识别能力由强到弱依次为PB信号、RB信号、NB信号、LB信号、AB信号。虽然对AB信号的识别能力最弱，但是该系统对AB信号的识别率仍然达93%。

表7 仿真实验结果

5 结束语

本文对心电信号的多重分形性与心律失常心电信号的分类识别进行了研究，主要研究内容如下。

1) 对5种信号进行多重分形分析，得出心电序列具有多重分形性质，并提出使用多重分形半波谱和广义 Hurst指数作为心电信号特征表示的假设，并通过相应的理论推导和实验，证明该假设是成立的。

2) 提出使用多重分形趋势波动分析的方法提取心电信号的特征，用这些特征作为神经网络分类器的特征向量输入。实验结果显示，用多重分形描述心电信号特征的方法是可行的，并且可以达到较高的准确率。

3) 构建了一个完整的心电信号自动标注系统。该系统能够自动识别出一段包含多个周期的心电序列，并将各个周期进行标注，并且该系统拥有较好的容错率。

[1] 王兴元, 朱伟勇. 人犬对比心电波形分维的研究[J]. 中国生物医学工程学报, 1998(3): 281-285.WANG X Y, ZHU Y W. A comparative study on the fractal dimension of ECG[J]. Chinese Journal of Biomedical Engineering,1998(3): 281-285.

[2] 王兴元, 顾树生. 心电动态生理及病理信息的非线性动力学研究[J]. 中国生物医学工程学报, 2000, 19(4): 397-403.WANG X Y, GU S S. Nonliear dynamics of ECG physiological and pathological information[J]. Chinese Journal of Biomedical Engineering, 2000, 19(4): 397-403.

[3] NING X, BIAN C, WANG J, et al. Research progress in nonlinear analysis of heart electric activities[J]. Chinese Science Bulletin,2006, 51(4): 385-393.

[4] MYTHILY V, GEETHA S. Neck cardiography and fractal analysis of its wavelet transform modified signal[J]. Indian Journal of Science and Technology, 2015, 8(31).

[5] BARABASI A L, VICSEK T. Multi-fractality of Self-affine Fractals [J]. Phys. Rev. A, 1991, 44: 2730-2733.

[6] KANTELHARDT J W, ZSCHIEGNER S A, KOSCIELNY-BUNDE E, et al. Multifractal detrended fluctuation analysis of nonstationary time series[J]. Physica A: Statistical Mechanics and Its Applications, 2002, 316(1): 87-114.

[7] MUKHOPADHYAY S, MANDAL S, DAS N K, et al. Diagnosing heterogeneous dynamics for CT scan images of human brain in wavelet and MFDFA domain[M]//Advances in Optical Science and Engineering. India Springer, 2015: 335-340.

[8] CATALANO L, FIGLIOLA A. Analysis of the nonlinear relationship between commodity prices in the last two decades[J]. Qualityamp; Quantity, 2015, 49(4): 1553-1558.

[9] XU Y, FENG H. Revisiting multifractality of TCP traffic using multifractal detrended fluctuation analysis[J]. Journal of Statistical Mechanics: Theory and Experiment, 2014, 2014(2).

[10] FARRELL R M, XUE J Q, YOUNG B J. Enhanced rhythm analysis for resting ECG using spectral and time domain techniques[C]//The IEEE/RSJ International Conference on Cornputers. 2003, 30(6):733-736.

[11] SUN Y, CHAN K L, KRISHNAN S M. Characteristic wave detection in ECG signal using morphological transform[J]. BMC Cardiovascular Disorders, 2005, 5(1): 7-19.

[12] SHYU L Y, WU Y H, HU W. Using wavelet transform and fuzzy neural network for VPC detection from the Holter ECG[J]. IEEE Transactions on Biomedical Engineering, 2004, 51(7): 1269-1273.

[13] KOHLER BU, HENNING C, ORGLMEISTER R. The principles of software QRS detection[J]. IEEE Engineering in Medicine and Biology Magazine, 2002, 21(1): 42-57.

[14] ADDISON P S. Wavelet transforms and the ECG: a review [J].Physiological Measurement, 2005, 26(5): 155-199.

[15] PAN J P, TOMPKINS W J. A real-time QRS detection algorithm[J].IEEE Transactions on Biomedical Engineering, 1985, 32(3):230-236.

[16] FALCONER K J. Fractal geometry: mathematical foundation and applications[M]. Chichester: John Wiley amp; Sons Ltd, 1990.

[17] 张永平. 分形的控制与应用[D]. 济南: 山东大学, 2008.ZHANG Y P. Fractal control and application[D]. Jinan: Shandong University, 2008.

[18] 杜必强. 振动故障远程诊断中的分形压缩及分形诊断技术研究[D]. 保定: 华北电力大学, 2009.DU B Q. Study on fractal compression and fractal diagnosis in remote diagnosis of vibration fault[D]. Baoding: North China Electric Power University, 2008.

[19] ARDUINI F, FIORAVANTI S, GIUSTO D D. A multifractal-baesd approach to natural scene analysis[C]//The 1991 International Conference on Acoustics, Speech, and Signal Processing, Piscataway.1991:2681-2684.

[20] CHENG Q. Generalized binomial multiplicative cascade processes and asymmetrical multifractal distributions[J]. Nonlinear Processes in Geophysics, 2014, 21(2): 477-487.

[21] GAUTAM M K, GIRI V K. A neural network approach and wavelet analysis for ECG classification[C]//2016 IEEE International Conference on Engineering and Technology(ICETECH). 2016: 1136-1141.

[22] GAUTAM M K, GIRI V K. An approach of neural network for electrocardiogram classification[J]. APTIKOM Journal on Computer Science and Information Technologies, 2016, 1(3): 115-123.

Design and application of electrocardiograph diagnosis system based on multifractal theory

ZHANG Chun-kai, YIN Ao, ZHANG Jing-wang, TIAN Pan-bo, ZHOU Ying, QI Chang-qing

(School of Computer Science and Technology, HITSZ, Shenzhen 518055, China)

An automatic segmentation algorithm for ECG data using differential threshold method was designed,which could identify the various ECG cycles of continuous ECG data. And it could obtain the multifractal features of multiple fractal and generalize hurst index feature of ECG data, these features were used to train artificial neural network in order to classify ECG data, the accuracy of the classifier could reach 97%. An ECG diagnosis system was implemented, which can automatically identify ECG sequences that contain multiple ECG cycles, and can automatically ignore the incomplete ECG cycle data, and could annotate every cycle of ECG data.

MFDFA, scale-free interval, multifractal, neural network

Shenzhen Foundation Research Project (No.JCYJ20170307151518535)

TP315

A

10.11959/j.issn.2096-109x.2017.00204

2017-07-24；

2017-09-20。

张春慨，ckzhang812@gmail.com

深圳市基础研究基金资助项目（No.JCYJ20170307151518535）

张春慨（1973-），男，山东烟台人，博士，哈尔滨工业大学（深圳）副教授，主要研究方向为流数据挖掘、网络信息安全以及互联网技术。

尹奥（1993-），男，河北邯郸人，哈尔滨工业大学（深圳）硕士生，主要研究方向为异常检测。

张景旺（1991-），男，黑龙江哈尔滨人，哈尔滨工业大学（深圳）硕士生，主要研究方向为流数据挖掘、异常检测。

田攀博（1993-），男，河南周口人，哈尔滨工业大学（深圳）硕士生，主要研究方向为数据挖掘、隐私感知。

周颖（1994-），女，湖南邵阳人，哈尔滨工业大学（深圳）硕士生，主要研究方向为数据挖掘。

齐常青（1991-），男，山东泰安人，哈尔滨工业大学（深圳）硕士生，主要研究方向为数据挖掘。