牵引负荷接入电力系统的随机潮流计算

乔 垚， 高锋阳， 杜 强， 黄 可， 强国栋

(兰州交通大学 自动化与电气工程学院 甘肃 兰州 730070)

DOI: 10.13705/j.issn.1671-6841.2017061

牵引负荷接入电力系统的随机潮流计算

乔 垚， 高锋阳， 杜 强， 黄 可， 强国栋

(兰州交通大学 自动化与电气工程学院 甘肃 兰州 730070)

基于随机潮流计算对含牵引负荷的电网潮流不确定性进行描述，提出使用群体感应机制的粒子群算法对牵引负荷概率模型进行参数辨识.采用基于Nataf变换的拉丁超立方采样技术控制随机潮流输入变量的相关性.结合算例仿真，分析在不同负荷空间相关性的情况下，牵引负荷的接入对电网电压和支路潮流概率分布的影响.结果表明，使用群体感应机制的粒子群算法参数辨识精度更高，且避免了基本粒子群算法易陷入局部最优解的缺点；考虑牵引负荷随机性的支路功率和电压概率分布因不同的负荷空间相关性变化明显.为新建高铁线路接入电网提供了参考.

牵引负荷； 粒子群算法； 拉丁超立方采样； 随机潮流计算

DOI: 10.13705/j.issn.1671-6841.2017061

0 引言

牵引负荷是一种单相电力负荷，具有随机性、单相独立性和不对称性，随着未来大量新建高速线路接入电力系统，牵引负荷功率的随机性将会给电网潮流分析带来挑战[1].采用概率统计的方法构建牵引负荷的概率模型可以较好地描述其功率的波动.文献[2]利用单台电力机车有功功率分布和行车密度分布联合对牵引变电所有功功率进行建模，并基于有功功率实测数据完成参数辨识.文献[3-4]针对牵引负荷引起的三相不平衡问题，建立了牵引变电所负荷以及负序电流概率模型.以上两种概率模型都是先假设负荷的随机变化服从已知分布，再用实测数据进行参数估计，没有考虑其他随机因素的影响.文献[5-6]使用非参数多变量核密度估计获得节点负荷联合概率密度模型，该方法无须任何先验知识，完全从数据样本出发研究数据分布特征，在负荷建模领域有着广泛应用.随机潮流通过概率统计的方法反映因负荷波动或发电机出力变化等不确定性因素所带来的影响[7]，该方法由Borkowska于1974年提出，现主要可以分为模拟法、点估计法和解析法.其中模拟法即蒙特卡洛法，基于简单随机采样的蒙特卡洛法(SRS-MCS)在采样样本足够大的情况下可以得到很高的精度，但缺点是耗时较多，如何在保证计算精度的前提下有效缩减计算时间是使用模拟法的关键.文献[8-9]采用拉丁超立方采样(Latin hypercube sampling,LHS)和Gram-Schmidt正交化方法提高采样效率，减小了采样矩阵列之间的相关性，降低了概率潮流的计算量.文献[10]针对LHS方法采样数量必须固定的限制提出了扩展拉丁超立方采样(extended LHS,ELHS)减少了确定性潮流计算的次数，提高了潮流计算的效率.传统的LHS只能针对输入变量相互独立的情况，但在真实的电网运行环境中，临近区域的负荷之间往往具有空间上的相关性.文献[11]提出了考虑输入变量相关性的概率潮流计算方法(correlation Latin hypercube sampling Monte Carlo simulation,CLMCS)处理输入变量间的相关性，并保留传统LHS采样耗时少、精度高的优点.为进一步减少LHS方法的采样时间，文献[12]针对正态分布变量的采样引入了区间均值采样方法，简化了LHS方法中的积分运算的过程.近年来模拟法不仅用以解决随机潮流问题，在评估电力系统概率可靠性[13-14]和微电网优化控制[15]等方面也得到了广泛的应用.

本文首先通过结合生物机制的粒子群算法对概率负荷模型参数进行辨识，其次基于Nataf变换控制输入随机变量之间的相关性.在此基础上，引入区间均值采样进一步提高采样计算效率.最后以IEEE9节点和IEEE30节点测试系统为例进行仿真分析，验证所提方法的有效性.

1 牵引负荷概率模型及其参数辨识

牵引负荷概率模型即利用功率的统计特性反映在一定时间范围内负荷功率的波动情况，图1给出了牵引负荷接入电力系统的示意图，所提概率模型即牵引变电所高压侧的等效功率模型.

图1 牵引负荷接入电力系统示意图Fig.1 Schematic diagram of traction load access to the power system

文献[16]提出了用单车有功功率叠加的思想构建其功率模型，

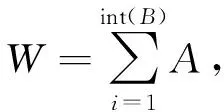
(1)

式中：A为单车有功功率，B为同时段机车数量，皆服从正态分布即牵引供电系统总的有功功率可以用单车功率的和来表示.模型中4个待辨识的参数分别为有功功率的期望值μp和标准差σp以及机车数量的期望μn和标准差σn，共同决定模拟数据的概率密度曲线的形态.

1.1群体感应机制粒子群算法原理

粒子群算法(PSO)是基于群体的智能优化方法，在赋予算法初值的基础上通过搜寻迭代获得适应度更优的解[17].将N个粒子随机散布在寻优空间的D个维度内，每个粒子分别通过Xi=(xi1，xi2，…，xiD)以及Vi=(vi1，vi2，…，viD)表征其所处的位置和运动状态，并用下式更新其位置：

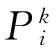
(2)

Xk+1=Xk+Vk+1，

(3)

式中：c1和c2为加速因子，r1和r2为(0～1)间的随机数；ω为惯性权重，它决定着粒子的运动状态能否轻易改变；Pi和Pg分别为当代每个粒子自身的最优值以及当代全部粒子的最优值，每个粒子通过追踪这两个极值来更新自身的速度和位置.基本PSO算法易陷入局部最优解，将生物机制与智能算法相结合被认为是一种有效改进算法性能的方法[18].群体感应机制的粒子群算法(PSOQS)是将微生物普遍存在的群体感应行为嵌入到基本PSO算法当中. 当原始种群繁殖到一定代数以后，感应产生一个与原种群规模相同的种群，感应种群繁殖一定代数后，将自身种群中适应度较好的个体与原种群中较差的粒子进行交换以达到“优胜劣汰”的目的.原种群在产生感应种群时暂时停止迭代，会额外增加计算时间，但该举措优化了整个解空间，提高了算法的性能.

1.2牵引负荷模型参数辨识

1.2.1适应度函数选取 适应度函数是用来评价每个粒子所代表解的优劣情况.根据概率密度统计结果所构建的适应度函数能够更加灵活地选择拟合目标，

(4)

式中：yi为所选实测牵引负荷有功概率密度曲线上拟合值的纵坐标；Δx为拟合点横坐标xi之间的间隔；Li为使用蒙特卡洛模拟所得的数据落在区间[xi-Δx,xi+Δx,]内的样本数量，LΣ为模拟数据的总量.即由式(1)所表述的模型借助蒙特卡洛模拟生成相应的数据，统计不同区间的概率密度值，并与实际对应的yi值作差进行比较，衡量当前粒子所代表解的优劣.因此，适应度函数的取值越小，粒子对应的参数值就越接近真值.

1.2.2算法求解过程 在上节的基础上，通过统计一组有功功率实测数据，求得式(4)中K个概率密度拟合值(xi,yi)，并通过下列步骤完成辨识过程：

1) 初始化参数，给每个粒子赋予位置和速度的初值，其中位置向量即4个待辨识的参数的值.

2) 将每个粒子的初值带入式(1)模型中，利用蒙特卡洛模拟数据，并由式(4)计算各个粒子的适应度值，得出未开始迭代时全局最优粒子所在的位置Pg，即初始随机分布粒子的最优解.

3) 开始迭代，由式(2)更新粒子的速度及位置，重复步骤2)，得出新一代个体最优值和全局最优值.

4) 到达感应群体衍生迭代次数后，产生感应群体.选择与原种群规模、参数一致的感应种群，并如前文所述，以一定的比例进行两个群体之间粒子的交换，优化解空间.

5) 检查是否到达最大迭代次数，输出全局最优粒子的位置，即模型参数的最优解.

2 基于Nataf变换的拉丁超立方抽样方法

传统的LHS采样是在假定输入变量相互独立的情况下进行采样和排序的，而实际电力系统中负荷之间具有一定的相关性.因此，学者提出了考虑输入变量相关性的拉丁超立方采样方法[11]，该方法由LHS以及输入变量相关性处理两部分组成，在保留原有LHS抽样法覆盖采样空间大优点的基础上，使得概率潮流运算的结果更加准确.

2.1基于正态随机变量的改进拉丁超立方抽样(improvedLHS,ILHS)

LHS方法实际上是通过对随机变量的分布函数求取反变换得到样本，文献[12]提出了基于正态随机变量的区间均值采样方法(ILHS).该方法针对正态分布的抽样计算量更小，样本均值和方差更为精确.

2.1.1一般负荷的采样 本文中设定负荷服从均值为μ、方差σ为正态分布，将分布函数取值范围[0，1]分为N个互不重叠的子区间，得到N+1个区间端点，这些端点由对应随机变量的分布函数的反函数求得对应随机变量的取值yi,n，

(i/N).

(5)

当输入变量服从正态分布时，第n个变量在其第i+1个等概率区间的平均值为：

μ.

(6)

通过将一般正态分布转化为标准正态分布，则式(6)计算更为简便，并得到一般形式正态分布的区间均值：

μ.

(7)

2.1.2基于牵引负荷模型的拉丁超立方采样 本文采用的牵引负荷概率模型为机车数量和单车功率的叠加，且二者均服从正态分布.在上节的基础上提出对该模型进行分层抽样，采样步骤如下所示：

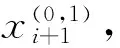
2) 从矩阵X第1个随机变量X1开始抽取对应的X1个功率样本,并按照式(1)的原理将X1个功率样本求和作为有功功率样本值之一.对功率层样本进行随机抽取，但是要限制X1中高频元素对应生成随机数的取值范围，更好地拟合功率的样本区间.

3) 将X中剩余机车数量样本值均按照步骤2)求得功率样本矩阵Y.

2.2Nataf变换

输入随机变量的相关性用相关系数矩阵来描述，即假设n个输入随机变量Xk，k=1,2,…,n的相关系数矩阵为CX，其中元素ρij为随机变量Xi和Xj的相关系数，可表示为：

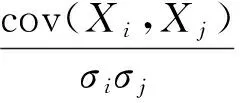
(8)

其中：σi和σj分别为随机变量Xi和Xj的标准差.由等概率转化原则引入标准正态分布的随机变量Zk，k=1,2,…,n，其相关系数矩阵为CZ：

(9)

式中:F(·)为随机变量Xk对应的累积概率分布函数，Φ(·)和Φ-1(·)分别为标准正态随机变量的累积分布函数和逆累积分布函数.由Nataf变换理论可知，CZ中的元素ρ0ij与CX中的元素ρij满足如下关系：

因此，通过Nataf变换控制输入随机变量相关性的核心思想是产生相关系数矩阵为CZ并且服从标准正态分布的样本Z，通过式(9)的反变换即可获得样本Xk.通过式(10)确定相关系数矩阵CZ后，对其进行Cholesky分解CZ=BBT，其中B为下三角矩阵.随机变量Z*若满足

Z*=BW,

(11)

式中:W=(W1,W2,…,Wn)为独立标准正态随机变量，则Z*的相关系数矩阵就是CZ.产生确定相关系数矩阵对应的Xk具体步骤如下：

1) 由CX中元素通过式(10)求得CZ中对应的元素ρ0ij.

2) 对CZ进行Cholesky分解得到下三角矩阵B.随机生成相互独立的标准正态样本W，由式(11)求得相关系数矩阵为CZ，并且服从标准正态分布的样本Z*.

3) 定义Z*的顺序矩阵为Ls，其每一行元素对应着Z*中相应行元素从小到大的排列顺序.由式(9)随机变量Xk与Zk之间的转换关系可知，将输入随机变量采样矩阵X=[X1,X2,…,Xn]的每一行按照Ls对应行的元素所指定的位置进行重新排列，得到的样本矩阵S的相关系数矩阵就近似等于CX.

对于不具备相关性的负荷节点使用Cholesky分解降低样本矩阵各行之间的相关性[14].首先初始化一个顺序矩阵Ls，其每一行元素为1～N整数的随机排列，代表采样矩阵对应行元素应该排列的位置.Ls各行对应的相关系数矩阵为ρL，因此通过Cholesky对其进行分解可得到下三角矩阵D，并由式(12)得到行相关性小于Ls的Gs:

Gs=D-1Ls.

(12)

重复上述步骤即可得到行相关性小于预定值的Gs.其次对输入随机变量进行ILHS采样，得到采样矩阵S′，并由Gs各行元素从小到大的顺序指导S′对应行元素重新排列.最终可得到相关性较低的采样矩阵S*.同时，为检验样本矩阵行之间的相关性程度，引入相关性系数矩阵方均根[14]，

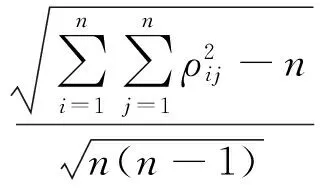
(13)

3 算例分析

3.1牵引负荷概率模型参数辨识结果

根据2.2节所述步骤，在matlab中编制程序，输出全局范围的最优解为(μp,σp,μn,σn)=(5.52,1.61,1.36,0.66).通过蒙特卡洛模拟生成该参数对应的概率密度曲线图，如图2虚线所示.并与实测数据概率密度直方图进行对比，结果表明该负荷概率模型能够较好地描述牵引负荷在一定时间范围内的概率统计特征.图3给出了分别采用基本粒子群算法和群体感应机制粒子群算法的适应度函数值随着迭代次数变化的对比图.可见，采用群体感应机制的粒子群算法较基本粒子群算法收敛速度更快，且群体最优粒子对应的适应度函数取值也优于基本PSO算法.在第二次发生群体感应时，基本已经完成寻优过程.因此通过将生物机制融入智能算法可以提高其运算性能，优化辨识结果.

3.2算例测试

为研究含有牵引负荷的电力系统潮流变化趋势，分别采用IEEE9和IEEE30节点算例在matlab平台下进行测试，具体计算步骤为：

1) 根据牵引负荷功率的统计数据，对式(1)所示概率模型进行参数辨识，得到模型参数.

2) 由具体算例中负荷的相关性矩阵CX经抽样得到采样矩阵S.

3) 将样本S矩阵中每一列作为输入随机变量带入潮流方程中，使用牛顿拉夫逊算法进行确定性潮流计算求出节点电压幅值和相角.

4) 样本矩阵每一列元素计算完毕后求出输出变量的数字特征，绘制累积概率分布曲线，比较牵引负荷接入前后对系统潮流的影响.

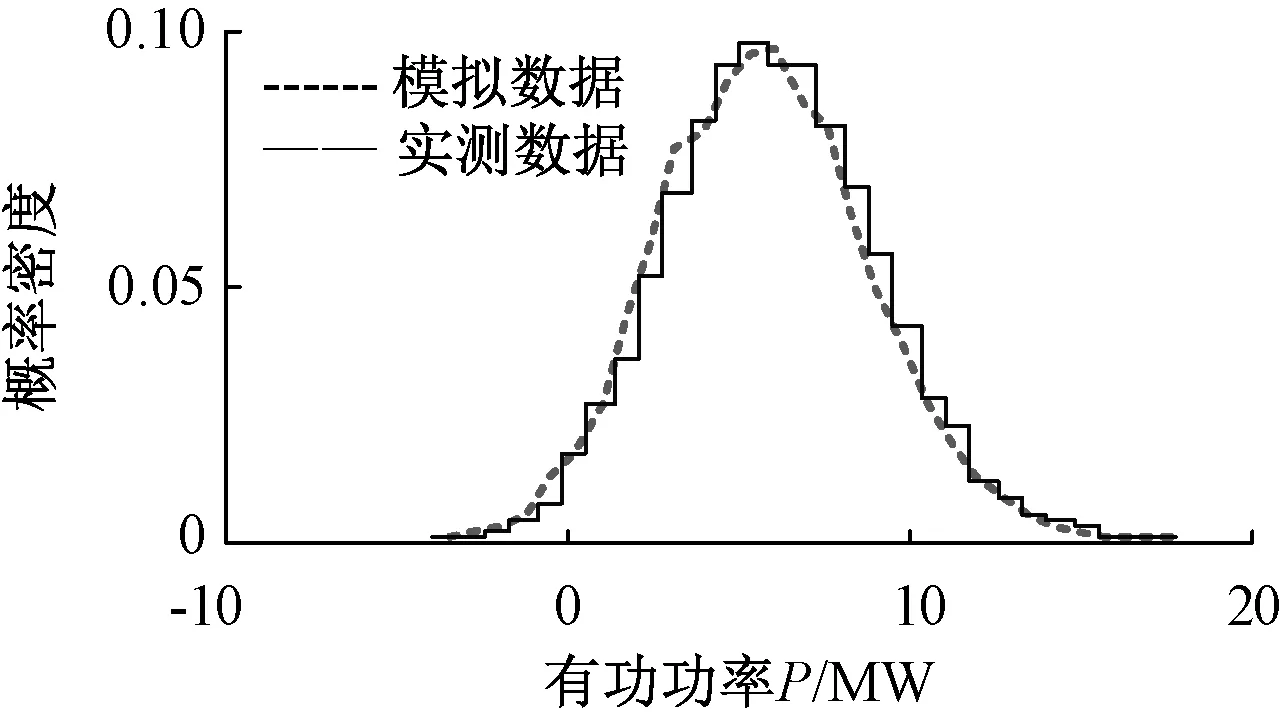
图2 某牵引变电站负荷实测概率密度与模拟数据对比Fig.2 The comparison between the measured probability density and the simulated data of a traction substation

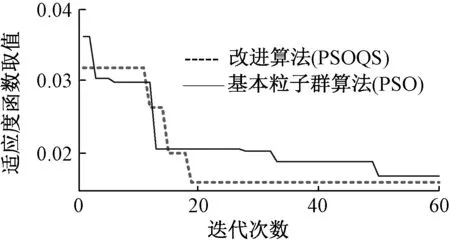
图3 适应度函数取值对比Fig.3 The comparison of fitness function values

为了验证计及牵引负荷随机潮流计算的算法性能，将通过1)～4)步骤所得的输出随机变量的μa和σa与由简单随机采样的蒙特卡洛模拟计算20 000次得到的准确值μs和σs进行比较，并由|μ和|σ表示相对误差：

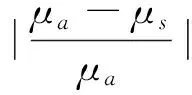
(14)

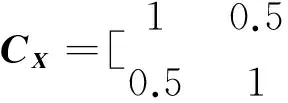
采用本文方法生成的负荷样本矩阵对应的相关性系数矩阵的方均根值为0.35，采样阵的方均根为0.31，采样矩阵各行之间的相关性基本得到了控制.

按照上节所提步骤进行概率潮流计算，图4～6给出9节点测试系统中进行概率潮流计算的结果.

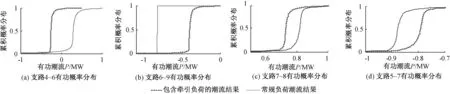
图4 接入牵引负荷前后有功概率潮流计算结果Fig.4 Calculation results of active power flow before and after traction load access

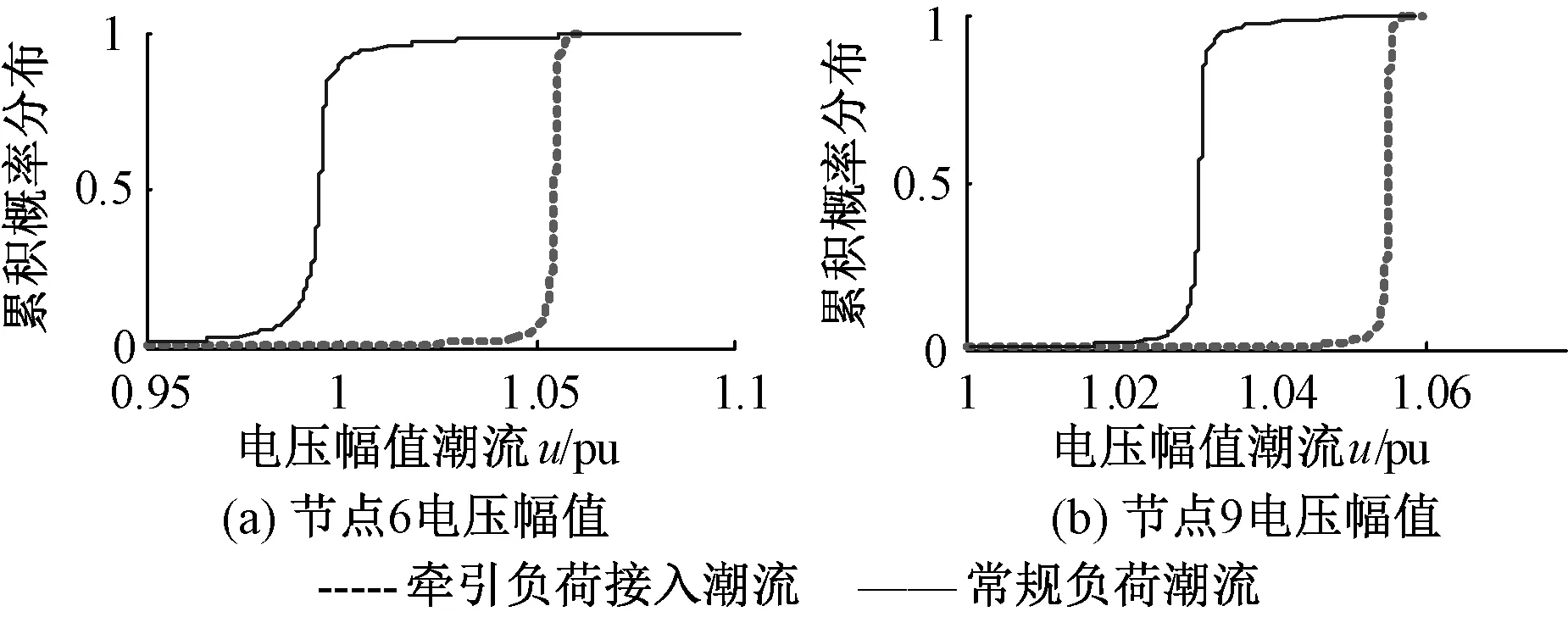
图5 接入牵引负荷前后电压幅值概率潮流计算结果Fig.5 Calculation results of voltage amplitude before and after traction load access

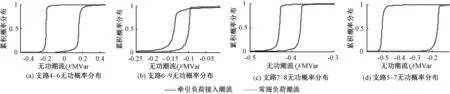
图6 接入牵引负荷前后无功概率潮流计算结果Fig.6 Calculation results of reactive power flow before and after traction load access

如图4(a)、(b)所示，牵引负荷接入后，支路4～6潮流反向，而相邻支路6～9功率潮流变化范围变大，但传输功率有所下降.支路功率值主要由支路所连接的节点电压以及该支路导纳所决定，对应节点电压幅值累积概率如图5(a)、(b)所示，牵引负荷接入后，节点6与节点9电压幅值均有上升.表1给出了节点6和节点9的越限概率值，可见牵引负荷接入后会导致接入点及相邻节点越限概率显著增大.图4(c)、(d)显示出距离牵引负荷接入点较远的支路潮流受到的影响较小.图6给出了支路无功功率的变化趋势，与该支路有功功率变化趋势相近.

表1 节点9测试系统牵引负荷接入前后电压越限概率比较

3.2.2IEEE30节点系统 在上节的基础上，为研究多组牵引负荷接入具有不同空间相关性的负荷区域对系统潮流的影响，将两组牵引负荷的功率数据接入IEEE30测试系统的16节点和17节点，如图7所示：

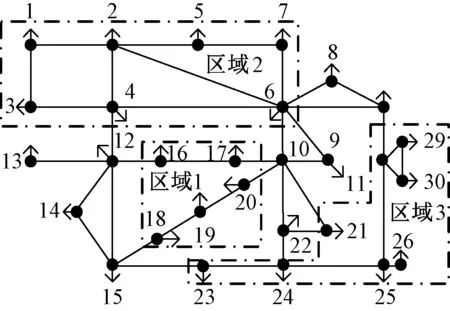
图7 IEEE30节点测试系统结构图Fig.7 IEEE30-bus test system

保持其他区域的负荷相互独立，仅改变区域1负荷之间的空间相关性，其对应的方均根值以及采样矩阵的方均根值如表2所示.

表2 采样矩阵行相关性方均根值对比

由表2可知区域1的负荷采样矩阵各行元素之间的空间相关性得到了较好的控制.图8给出了区域1不同的空间相关性的负荷对应的潮流计算结果.

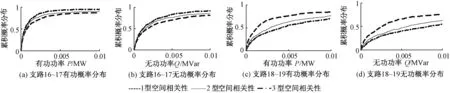
图8 不同空间相关性的区域负荷概率潮流计算结果Fig.8 Results of regional load probabilistic power flow calculation with different spatial correlation

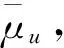
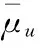
表3 30节点测试系统不同空间相关性17节点电压幅值平均值对比

图9给出了使用本文方法得到节点17电压幅值的累积概率分布曲线与使用随机采样的蒙特卡洛方法所得结果对比，结合图9并由式(14)、(15)求得|μ和|σ分别为0.02和0.04.同时，使用本文方法在确定负荷相关性下计算时间为45 s,而使用蒙特卡洛模型随机抽样方法的计算时间为176 s.因此本文考虑牵引负荷的随机潮流算法在保证精度的同时可以有效提高算法的效率.图10给出了3种空间相关性下节点17电压幅值的对比，可以看出牵引负荷对电压幅值下限附近的值影响较为明显，即空间相关性较强时，电压下限附近的值较少，对应了表3所得结果.

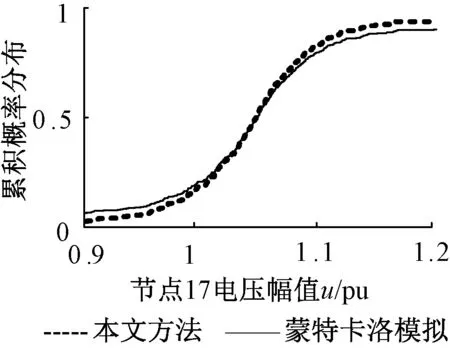
图9 本文方法与蒙特卡洛模拟的对比Fig.9 Comparison of this method with Monte Carlo simulation

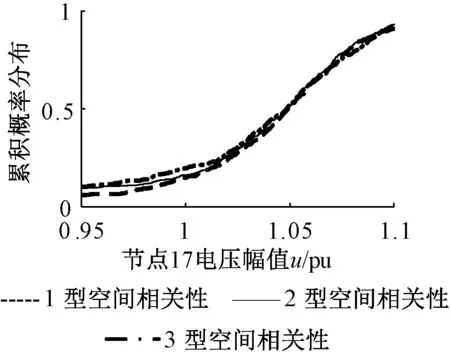
图10 节点17电压幅值概率潮流计算结果Fig.10 The node voltage amplitude probability of 17 probabilistic power flow calculation results

4 结论

针对牵引负荷的随机性对电网潮流的影响，模拟牵引负荷接入不同结构电网，使用随机潮流算法分析该区域潮流的变化趋势，采用结合群体感应机制的粒子群算法辨识模型参数，兼顾牵引负荷接入区域的负荷在空间上的相关性以获取随机输入变量样本，进行概率潮流计算测试，得到如下结论：

1) 结合群体感应机制的粒子群算法对牵引负荷概率模型进行参数辨识，所得模型精度更高，且避免了基本粒子群算法易陷入局部最优解的缺点.

2) 通过使用Nataf变换，并结合ILHS采样能够有效控制输入变量的相关性，可在有限的采样次数里保证计算精度，有效提升随机潮流的计算效率.

3) 牵引负荷因其较强的随机性会导致接入支路概率潮流变化明显，并使接入节点电压幅值越限概率增加.同时，改变负荷的空间相关性对支路潮流和电网电压影响较为显著.后续工作应兼顾牵引负荷在时间和空间上的相关性，并针对无功功率和负序电流进行建模，更加精确地模拟牵引负荷动态接入电网.

[1] 张丽艳, 李群湛, 朱毅. 新建电气化铁路牵引负荷预测[J]. 西南交通大学学报, 2016, 51(4):743-749.

[2] 杨少兵, 吴命利. 电气化铁道牵引变电所负荷概率模型[J]. 电力系统自动化, 2010, 34(24):40-45.

[3] 王斌, 张民, 邱忠才,等. 基于实测数据的高铁牵引变电所负序电流概率分析[J]. 西南交通大学学报, 2015, 50(6):1137-1142.

[4] 王斌, 张民, 高仕斌,等. 高速铁路牵引供电系统负序概率模型[J]. 电力系统及其自动化学报，2015, 27(6):56-61.

[5] 赵渊, 张夏菲, 周家启. 电网可靠性评估的非参数多变量核密度估计负荷模型研究[J]. 中国电机工程学报, 2009, 29(31):27-33.

[6] 颜伟, 任洲洋, 赵霞,等. 光伏电源输出功率的非参数核密度估计模型[J].电力系统自动化, 2013, 37(10):35-40.

[7] 丁明, 李生虎, 黄凯. 基于蒙特卡罗模拟的概率潮流计算[J]. 电网技术, 2001(11):10-14.

[8] 于晗, 钟志勇, 黄杰波,等. 采用拉丁超立方采样的电力系统概率潮流计算方法[J]. 电力系统自动化, 2009, 33(21):32-35.

[9] YU H, CHUNG C Y, WONG P, et al. Probabilistic load flow evaluation with hybrid latin hypercube sampling and cholesky decomposition[J]. IEEE transactions on power systems, 2009, 24(2):661-667.

[10] 丁明, 王京景, 李生虎. 基于扩展拉丁超立方采样的电力系统概率潮流计算[J]. 中国电机工程学报, 2013, 33(4):163-170.

[11] 陈雁,文劲宇,程时杰. 考虑输入变量相关性的概率潮流计算方法[J].中国电机工程学报, 2011,31(22):80-87.

[12] 张建平, 张立波, 程浩忠,等.基于改进拉丁超立方抽样的概率潮流计算[J]. 华东电力, 2013, 41(10):2028-2034.

[13] 侯雨伸, 王秀丽, 刘杰,等.基于拟蒙特卡罗方法的电力系统可靠性评估[J]. 电网技术, 2015, 39(3):744-750.

[14] 蒋程, 王硕, 王宝庆,等. 基于拉丁超立方采样的含风电电力系统的概率可靠性评估[J]. 电工技术学报, 2016, 31(10):193-206.

[15] 段玉兵, 龚宇雷, 谭兴国,等. 基于蒙特卡罗模拟的微电网随机潮流计算方法[J]. 电工技术学报, 2011(s1):274-278.

[16] 杨少兵, 吴命利. 基于改进蚁群算法的客运专线电力负荷建模与参数辨识[J]. 中国电机工程学报, 2015, 35(7):1578-1585.

[17] 沈良雄. 基于改进粒子群算法的电力负荷模型参数辨识研究[D]. 大连：大连海事大学, 2013.

[18] 程军. 基于生物行为机制的粒子群算法改进及应用[D]. 广州：华南理工大学，2014.

(责任编辑：王浩毅)

ProbabilisticPowerFlowoftheTractionLoadAccessingtothePowerSystem

QIAO Yao, GAO Fengyang, DU Qiang, HUANG Ke, QIANG Guodong

(SchoolofAutomationandElectricalEngineering，LanzhouJiaotongUniversity，Lanzhou730070,China)

Particle swarm optimization based on population induction was proposed to identify the traction load probabilistic model. The correlation of input variables could be controlled through the latin hypercube sampling based on Nataf transformation. Combined with numerical simulation and in the case of the different space correlation of the loads, analyzing the influence of traction load access on the voltage and branch power flow probability distribution was analyzed. The result showed that particle swarm optimization algorithm based on population induction was more accurate, which could overcome the disadvantage that the ordinary particle swarm algorithm was easy to fall into local optimum.The probability distribution of branch power and voltage considering the randomness of traction load was obviously different due to different loads spatial correlation. This study provided a reference for the new high-speed rail line accessing to the power system.

tractive load; particle swarm optimization; latin hypercube sampling; probabilistic load flow

2017-03-27

甘肃省科技支撑计划项目(1204GKCA038).

乔垚(1993—)，男，陕西榆林人，主要从事牵引供电系统建模研究，E-mail:qy_lzjtu@163.com.

TM92

A

1671-6841(2017)04-0104-08