赋Luxemburg范数的Musielak-Orlicz-Sobolev空间中的凸性

季丹丹

(牡丹江师范学院 数学科学学院，黑龙江 牡丹江 157011)



赋Luxemburg范数的Musielak-Orlicz-Sobolev空间中的凸性

季丹丹

(牡丹江师范学院 数学科学学院，黑龙江 牡丹江 157011)

克服了Musielak-Orlicz-Sobolev空间的结构复杂性,吸取了Musielak-Orlicz空间中凸性的研究方法,给出并证明了赋Luxemburg范数的Musielak-Orlicz-Sobolev空间具有严格凸性的充要条件.

Musielak-Orlicz-Sobolev空间; 严格凸性;Luxemburg范数;Δ2条件

1 基础知识

凸性是Banach空间几何理论基本内容之一，具有鲜明的直观几何意义. 凸性的研究最早是从Banach空间单位球的研究开始的. Clarkson[1]于1936年引入了一致凸空间并在这种空间中讨论了向量测度，为这方面的研究指明了方向. 而后引入了各种凸性，并讨论了它们的基本性质以及在最佳逼近和不动点理论中的应用. Musielak-Orlicz-Sobolev空间是一类复杂的Banach空间，本文将给出该空间中凸性的研究.

关于Musielak-Orlicz函数、函数的模、函数的Luxemburg范数、Musielak-Orlicz函数M所满足的Δ2条件，以及Musielak-Orlicz空间的定义见文献[2-3]；对于Musielak-Orlicz-Sobolev空间

Wm,M(Ω)={u∈LM(Ω):∂αu∈LM(Ω),

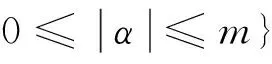
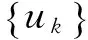
(1)

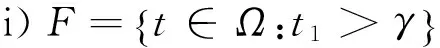
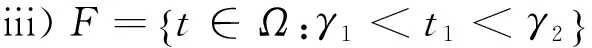
在下文中, 若M∉Δ2,只考虑情形i), 其他两种情况不予考虑.

在本文中令

则称v是M关于t的非严格凸点. M关于t的非严格凸点全体记为Kt(见文献[3]).

2 主要结果

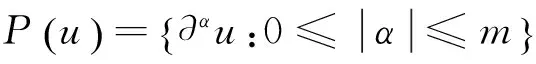
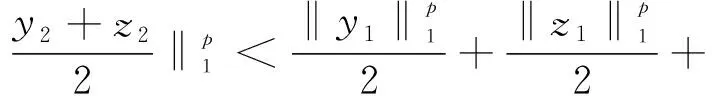
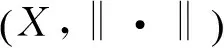
定理1 Wm,M是严格凸的充要条件是

(a) M∈Δ2；

证明 充分性.注意到实数集是凸集，由文献[3]中定理5.11知LM是严格凸的，又由引理1知Wm,M是严格凸的.

必要性.用反证法.先证明充要条件(b).

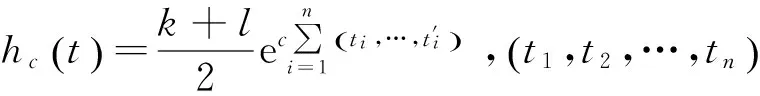
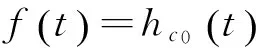
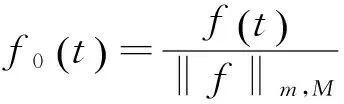
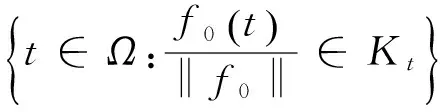
从而

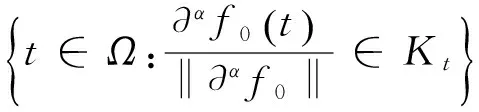
所以

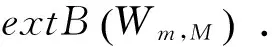
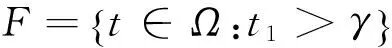
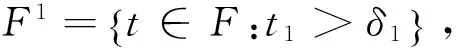
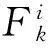
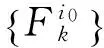
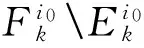
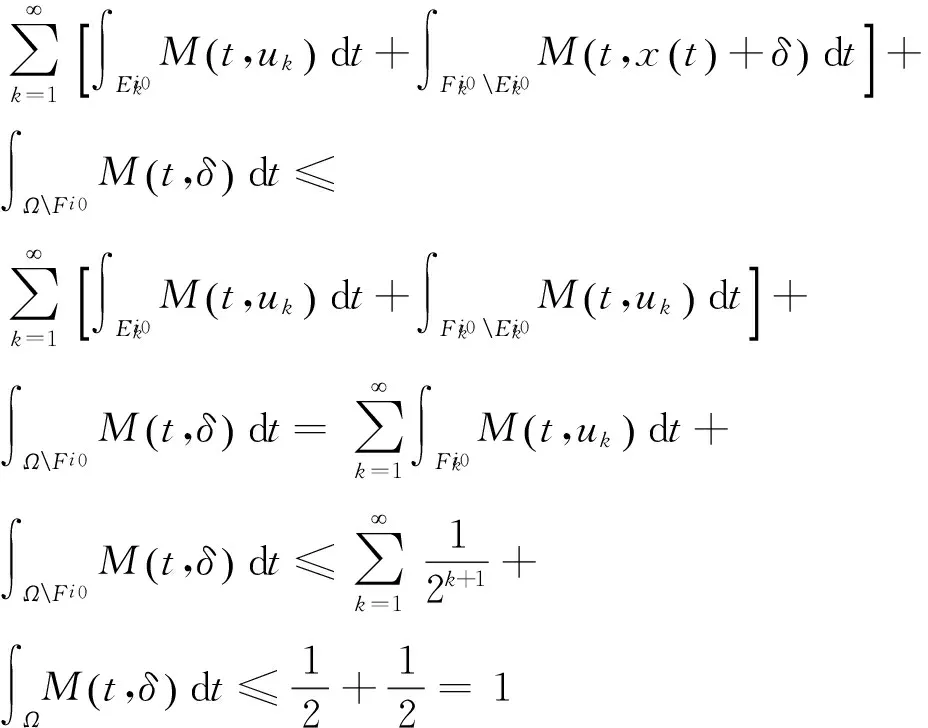
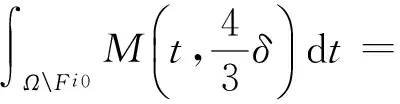
类似可证‖z‖≤‖x+f‖≤1.

这与Wm,M是严格凸的矛盾.故M∈Δ2.

[1]CLARKSON J A. Uniformly convex spaces[J]. Trans. Math. Soc, 1936，40: 396-414.

[2] HUDZIK H, LIU X B, WANG T F. Points of monotonicity in Musielak-Orlicz function spaces endowed with the Luxemburg norm[J]. Arch.Math, 2004, 82: 534-545.

[3] CHEN S T. Geometry of Orlicz paces[M].[S.l.]:Dissertations Mathematicae Warszawa, 1996.

[4]季丹丹, 贺鑫, 王玉文. Musielak-Orlicz-Sobolev空间中的单调性[J]. 数学的实践与识, 2013, 43(23): 213-218.

[5] 赵静, 陈述涛. Orlicz-Sobolev空间的中点局部一致凸性[J]. 数学杂志, 2005, 25(5): 567-570.

[6]陈述涛, 胡长英. Orlicz-Sobolev空间关于Luxemburg范数的端点与严格凸性[J]. 哈尔滨师范大学自然科学学报, 2001, 17(2): 1-6.

(编辑：郝秀清)

Rotundity in Musielak-Orlicz-Sobolev spaces with Luxemburg

JI Dan-dan

(School of Mathematical Sciences, Mudanjiang Normal College,Mudanjiang 157011,China)

This article is to overcome the difficulties of the structure, and adopt the research methods of rotundity in Musielak-Orlicz spaces. Necessary and sufficient conditions for rotundity of Musielak-Orlicz-Sobolev spaces with Luxemburg norm are given and proved.

Musielak-Orlicz-Sobolev spaces;rotundity;Luxemburg norm;condition Δ2

2016-02-25

牡丹江师范学院一般项目(YB201604); 牡丹江市科学技术项目(G2015K1980)

季丹丹, 女,jidandan1014@126.com

1672-6197(2017)01-0039-04

O

A