基于L1-范数的非线性TSVR①

许颖春 范丽亚

(聊城大学 数学科学学院,山东 聊城 252059)

基于L1-范数的非线性TSVR①

许颖春 范丽亚

(聊城大学 数学科学学院,山东 聊城 252059)

为了进一步降低TSVR的计算复杂性, 加快其学习速度, 本文利用L1-范数将TSVR的两个原始二次规划问题转化为线性规划问题, 并提出了基于L1-范数的TSVR(L1-TSVR). 实验结果表明L1-TSVR是一个有效的、可竞争的回归方法.

L1-范数，孪生支持向量回归机，回归函数，误差

作为一种通用学习方法，支持向量机(Support Vector Machine, SVM)[1-3]由于良好的泛化能力，已在诸多领域得到了广泛应用，如文本分类、语音识别、生物信息、时间序列分析、信号处理、遥感图像分析、个人信用评估等. 支持向量回归机(Support Vector Regression Machine, SVR)[4-6]是基于SVM发展起来的, 多用于数据(时间序列)的分析、拟合和回归, 其计算复杂性为8O(m3)，其中m是训练样本的个数. 有关SVM和SVR的基本理论和方法可参看文献[7,8]. 我们知道, 在大量数据中挖掘有用信息往往是非常困难的, 且得到的信息又是庞大的, 如果直接利用这些庞大的信息来进行数据分析, 常会导致算法的学习时间过长, 甚至失效. 为此, 学者们提出了诸多加快SVR的学习方法, 如TSVR[9,10],ε-TSVR[11-13]及其变形等. 尽管TSVR的计算复杂性理论上快SVR近4倍, 但随着样本个数的增加, TSVR的学习时间会急剧增加. 为了进一步降低TSVR的计算复杂性, 且不损失大的回归精度, 本文受文献[14,15]的启发, 提出了基于L1-范数的TSVR(L1-TSVR).

1 非线性TSVR

线性TSVR是通过引入两个Vapnikε-不敏感损失函数来构造两个小规模的QPPs, 并通过这两个QPPs来学习回归函数f(x). 具体地说, 线性TSVR是通过构建下面两个QPPs:

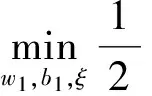
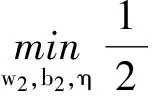
由于在实际应用中遇到的大部分回归问题都是非线性回归问题, 需要寻找非线性回归函数. 因此, 借助于核函数和核技巧, Peng[9]将线性TSVR推广到非线性形式. 非线性TSVR是通过构建下面两个QPPs

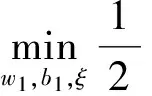
(1)

(2)

其中Kx=[k(x1,x),k(x2,x),…,k(xm,x)]. 于是, 模型(1)和(2)可转化为

(3)

(4)

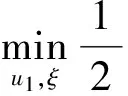
(5)

(6)

通过求解模型(5)和(6)的Wolfe对偶形式

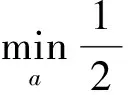
(7)

(8)

便可得到

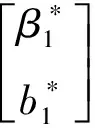
(9)

算法1非线性TSVR

步2 选择适当的核函数和核参数.

步3 求解模型(7)和(8), 分别得最优解α*,γ*∈Rm.

步6 构造回归函数f(x)=(f1(x)+f2(x))/2.

2 非线性L1-TSVR

算法1的计算复杂性是2O(m3). 随着训练样本个数m的增加, 其学习速度会急剧减慢. 为了降低算法1的计算复杂性, 本节利用L1-范数来稀疏模型(5)和(6), 得到下面两个线性规划模型

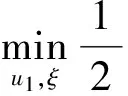
(10)

(11)

这时有u1=(GGT+δId+1)-1G(f-r1+s1),u2=(GGT+δId+1)-1G(h-r2+s2)且

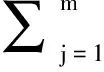
(12)

其中δ>0是正则化参数. 利用(12)式，模型(10)和(11)可放松为

(13)

(14)

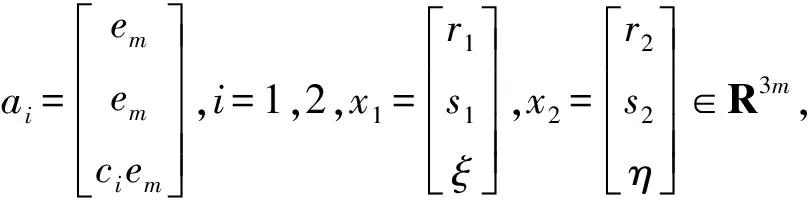
(15)

(16)

通过求解模型(15)和(16)得到回归函数的方法称为非线性L1-TSVR. 具体算法如下.

算法2非线性L1-TSVR

步2 选择适当的核函数和核参数.

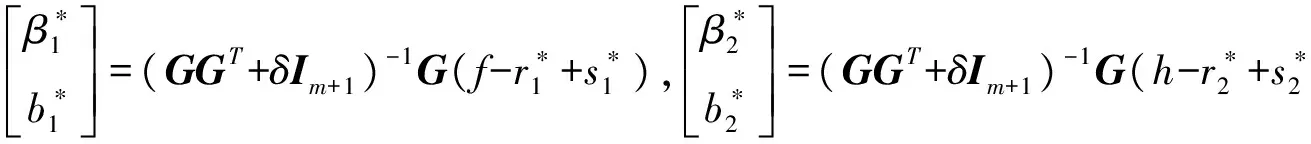
步6 构造回归函数f(x)=(f1(x)+f2(x))/2.

算法2与算法1的本质不同在于: 算法2的原始问题可放松为两个线性规划问题, 而算法1的两个原始问题是二次规划问题, 因此, 算法2加快了算法1的学习速度. 另一方面, 由于算法2 是求解两个松弛问题, 回归精度上可能会有一些损失. 一般来讲, 加快算法的学习速度往往以损失回归精度为代价, 但希望损失的精度越小越好, 如果损失的精度过大, 速度再快也不能称为是一个好算法.

3 实验与结果分析

表1 模型参数和正则化参数的选择

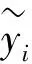
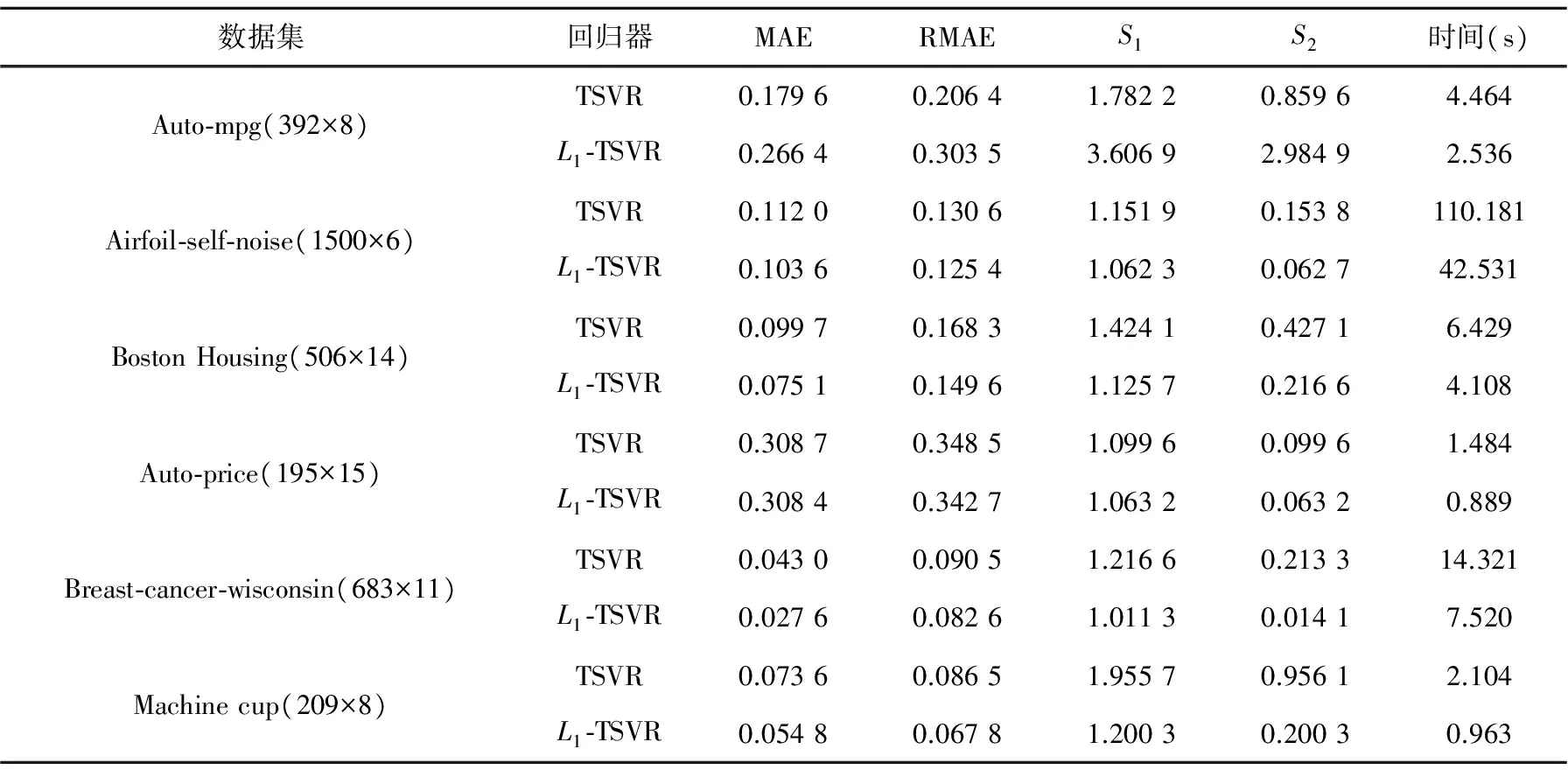
表2 实验结果

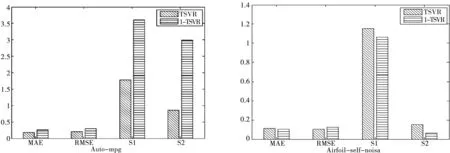
图1 误差柱形图

从表2中可以看出,L1-TSVR的学习时间明显少于TSVR的学习时间. 从表2和图1中可以看出,对Auto-mpg数据集, TSVR的回归精度在四个评价指标下均高于L1-TSVR. 对其余5个数据集,L1-TSVR的回归精度在MAE, RMAE和S1三个指标下均高于TSVR. 对指标S2, 在6个数据集下, TSVR的回归精度都高于L1-TSVR. 除此之外, 在最常用的两个评价指标MAE和RMAE下,L1-TSVR和TSVR的回归精度差距不明显. 因此, 可以说L1-TSVR是一个有效的、可竞争的回归方法.

4 结论

基于SVR的学习算法的计算复杂性是能否快速分析和处理数据的一个很重要的因素. 不同于SVR需要求解一个大规模的QPP, TSVR只需求解两个小规模的QPPs, 其整体计算复杂性为2O(m3), 其中m是训练样本的个数, 大约是SVR的4倍. 即使这样, 随着个数m的增加, TSVR的学习时间也会急剧增加, 甚至失效. 为了进一步降低TSVR的计算复杂性, 加快其学习速度, 本文利用了L1-范数将其原始问题中的两个QPPs转化为线性规划问题, 并提出了L1-TSVR.L1-TSVR的整体计算复杂性仅为2O(m), 因此其加快了TSVR的学习速度. 6组数据集上的实验结果表明,L1-TSVR的回归精度与TSVR的回归精度相差并不大, 尤其是对MAE, RMAE和S1这三个常用的评价指标来说, 除Auto-mpg数据集外,L1-TSVR的回归精度均高于TSVR的回归精度. 本文所用方法具有一定的普适性, 可用于稀疏其他TSVR型回归算法.

[1] Cortes C，Vapnik V N.Support vector networks[J]. Machine Learning，1995, 273-297.

[2] Vapnik V N.Statistical Learning Theory[M]. NY: John Wiley&Sons,1998.

[3] Weston J, Watkins C.Multi-class Support Vector Machine[M]. MA: MIT Press,1999.

[4] Scholkopf B, Tsuda K, Vert J P.Kernel Methods in Computational Bjology[M]. MIT Press, Cambridge. 2004.

[5] Terrault,Tarek I Hassanein.Management of the patient with SVR[J]. Journal of Hepatology,2016,S120-S129.

[6] Liu Yuan，Wang Rui-xue. Study on network traffic forecast model of SVR optimized by GAFSA[J]. Chaos, Solitons & Fractals,2016,89:153-159.

[7] 邓乃扬, 田英杰.数据挖掘中的新方法: 支持向量机[M].北京: 科学出版社, 2006.

[8] 夏文静,陈耿,范丽亚.八种最小二乘SVM型学习算法的优势比较[J].聊城大学学报:自然科学版,2016,29(2):14-16.

[9] Peng Xin-jun. TSVR: An efficient Twin Support Vector Machine for regression[J].Neural Networks, 2010, 23: 365-372.

[10] 李艳蒙,范丽亚.四种TSVR型学习算法的性能比较[J].聊城大学学报:自然科学版,2016,29(3):13-15.

[11] ShaoYuan-hai, Zhang Chun-hua,Yang Zhi-min, et al.An twin support vector machine for regression[J].Neural Comput & Applic, 2013, 23:175-185.

[12] Hao Pei-yi.Pairing support vector algorithm for data regression[J]. Neurocomputing,2017,225:174-187.

[13] Ye Ya-fen,Bai Lan.Weighted Lagrange ε-twin support vector regression[J]. Neurocomputing,2016,197:53-68.

[14] H Hua-juan, W Xiu-xi, Z Yong-quan.A sparse Method for Least Squares Twin Support Vector Regression[J]. Neurocoming，2016, 211: 150-152.

[15] Bai Lan, Wang Zheng, Shao Y H, et al. A novel feature selection method for twin support vector machine[J]. Knowledge-Based Systems，2014, 59: 1-4.

NonlinearTSVRBasedonL1-norm

XU Ying-chun FAN Li-ya

(School of Mathematical Sciences, Liaocheng University, Liaocheng 252059，China)

In order to reduce the computational complexity and accelerate the learning speed of TSVR, in this paper, the original quadratic programming problems of TSVR are translated into linear programming problems by means ofL1-norm, and then TSVR based onL1-norm (L1-TSVR) is presented. Experiment results indicate thatL1-TSVR is an effective and competitive regression method.

L1-norm, twin support vector regression machine, regression function, error

2017-05-10

国家自然科学基金项目(11501278); 山东省自然科学基金项目(ZR2016AM24)资助

范丽亚,E-mail:fanliya63@126.com.

O224

A

1672-6634(2017)03-0006-06