N,N-二甲基甲酰胺+醇二元混合物的黏度测定与关联
2017-11-22凌锦龙王俊毅黄慧波孙来玉陆欣悦
凌锦龙,王俊毅,黄慧波,孙来玉,陆欣悦
(湖州师范学院生命科学学院,浙江 湖州 313000)
N,N-二甲基甲酰胺+醇二元混合物的黏度测定与关联
凌锦龙,王俊毅,黄慧波,孙来玉,陆欣悦
(湖州师范学院生命科学学院,浙江 湖州 313000)
在288.15~313.15 K和常压下,利用乌氏黏度计测定了N,N-二甲基甲酰胺(DMF)分别与乙醇、丙醇、乙二醇和1,2-丙二醇组成的二元系全浓度范围内的黏度,计算了过量黏度Δη和过量流动活化自由能ΔG*E。用Redlich-Kister方程对过量黏度进行了关联;用黏度模型如Frenkel方程,Grunberg-Nissan方程,Katti-Chaudhari方程和McAllister方程对实验黏度数据进行了关联和预测,并利用Eyring理论方法计算了流动活化自由能、活化焓和活化熵等热力学函数。结果表明,4个二元系的过量黏度和过量流动活化自由能均为负值,且都随温度降低而偏差增大。过量黏度最低值均发生在DMF摩尔分数约为0.3处。McAllister模型对黏度数据的关联结果最好,预测值与实验值的平均相对偏差最小。比较并分析了 DMF与一元醇和二元醇之间分子相互作用的差异。。
N,N-二甲基甲酰胺;黏度;过量黏度;过量流动活化自由能;活化焓;活化熵
引 言
黏度是表征液体性质相关的阻力因子,是重要的迁移性质之一,在化学分离、传热、传质和流体流动等领域具有重要的指导作用。N,N-二甲基甲酰胺(DMF)是非质子的极性惰性溶剂,具有较大的偶极矩、高介电常数以及良好的氢键供体-受体性质,能够溶解多种有机和无机物质,广泛应用于制造合成纤维、皮革、薄膜和表面涂层等各种工业过程中。DMF与醇形成的混合体系由于醇分子的自缔合,以及不同种极性分子之间的交联缔合,具有高度的非理想性[1-5]。已有大量的溶液模型可用来描述这些效应和分子间相互作用[6-13]。其过量热力学性质之一的过量黏度提供了关于结构、特定分子间相互作用的程度和混合溶剂的相互作用等信息,对理解溶剂性能有重要意义[14-18]。
含 DMF混合溶剂性质的研究一直以来得到广泛关注[19-23]。Venkatesu[24]和 Shokouhi 等[25]综述了DMF与其他溶剂的分子相互作用以及对溶液物化性质的贡献。Zarei等[2]研究了N,N-二甲基甲酰胺、N-甲基甲酰胺与 1,2-丙二醇形成的二元和三元混合物的体积效应和黏度行为,分析了分子间力的强弱,分子大小和形状对混合液性质的影响。Jóźwiak等[14]探查了 DMF+水混合溶剂中冠醚(18-Crown-6)的热力学性质和黏度行为。Mohammad等[26-27]测定了DMF+烷醇(C5~C10)二元系的黏度性质,研究了烷醇链长和温度对黏度的影响。
为进一步理解 DMF-醇二元系的分子相互作用及对溶液黏滞性质的影响,本文以DMF+一元醇(乙醇、丙醇)、DMF+二元醇(乙二醇、1,2-丙二醇)为体系,测定了二元系在288.15~313.15 K下全浓度范围内的黏度,计算了过量黏度和过量流动活化自由能,利用半经验的黏度模型对实验黏度数据进行关联和预测。分析并探讨过量性质的变化及DMF与一元醇和二元醇之间分子相互作用的差异。
1 实验部分
1.1 试剂
N,N-二甲基甲酰胺(DMF,>99.9%,Aladdin试剂),乙醇(EtOH,>99.8%,Aladdin试剂),丙醇(PrOH,>99.0%,汕头西陇化工厂),乙二醇(EG,>99.8%,无锡海硕生物有限公司),1,2-丙二醇(12PD,>99.0%,如皋市金陵试剂厂),实验用水为石英亚沸蒸馏水。
1.2 实验过程
利用乌氏黏度计测定黏度。黏度计毛细管内径0.57 mm,循环式超级恒温槽,控温精度±0.05 K,秒表计时精度 0.01 s。计算式为η=η0ρt/(ρ0t0),η、ρ和t分别为待测液体黏度、密度和流经毛细管时间,η0、ρ0和t0分别代表水的相应变量。重复测量5次以上,每次相差不超过0.05 s,取平均值。黏度测量精度为±0.2%。
密度用10 ml的比重瓶(德国ISOLAB生产)在恒温条件下称重测量。电子天平称量精度±1×10-4g,密度测量精度为±0.05%。
二元混合溶液采用称重法配制。利用上述方法常压下测定了试剂在298.15 K时的黏度和密度,与文献值比较,两者吻合甚好(表1),说明本实验所用仪器和测定方法可靠。
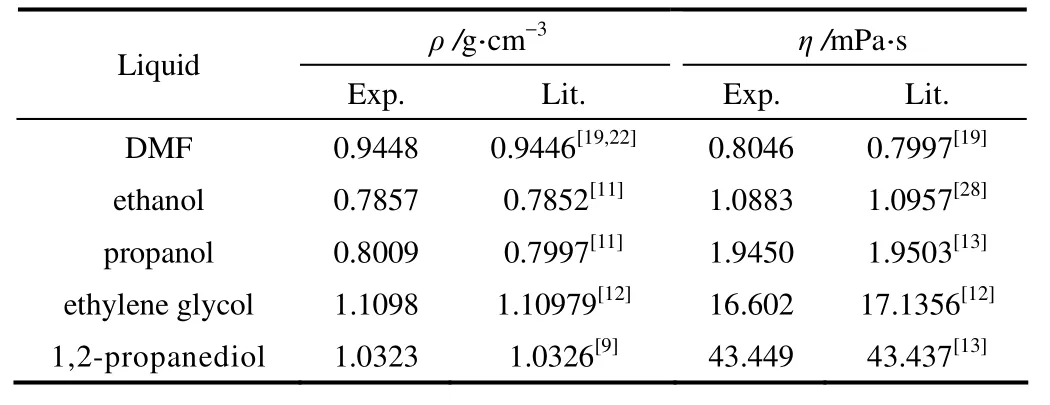
表1 298.15 K时试剂密度和黏度Table 1 Densities and viscosities of pure liquids at 298.15 K
2 结果与讨论
2.1 二元系的黏度
实验测定4个二元系DMF(1)-乙醇(2)、DMF(1)-丙醇(2)、DMF(1)-乙二醇(2)和 DMF(1)-1,2-丙二醇(2)在 288.15~313.15 K下的密度和黏度分别列于表2~表5。
二元混合物过量黏度Δη、过量流动活化自由能ΔG*E分别按式(1)和式(2)计算

式中,η为混合液黏度,x为摩尔分数,V为混合液摩尔体积,R为气体常数,T为热力学温度。下角标1和2分别表示组分1和组分2的相应性质。计算值一并列于表2~表5。

表2 DMF(1)-乙醇(2)二元系在不同温度下的黏度、过量黏度和过量流动活化自由能Table 2 Viscosities, excess viscosities and excess Gibbs energy of activation for viscous flow of DMF(1)-ethanol(2) system from 288.15 K to 313.15 K
4个体系的过量黏度均为负值(图1~图4),并随温度降低而偏差增大,最低点都出现在富醇区,约在x1=0.3处。同一温度同一组成下,在同类型的醇体系中,过量黏度随醇碳链增加而偏差更大,如DMF-丙醇的过量黏度的绝对值比 DMF-乙醇大,DMF-12PD体系的比DMF-EG大。过量黏度的负值常常是由于分子形状和大小以及形成聚集体的能力等引起,而较大的过量黏度值表明分子间存在强的作用力,如偶极-偶极相互作用,醇分子之间的氢键,醇分子和酰胺分子之间的氢键等。Uddin等[3]认为烷基醇单体内部可以形成环状或链状的复合物,随着—CH2基团的增加,环状复合物的比例也增加,单体醇结构破坏效应增强,分子间结合度随之下降,黏度降低;DMF和醇都是极性分子,分子间的偶极-偶极作用,会导致混合时形成溶剂-助溶剂加合物,而随温度的升高,参与形成加合物的分子振动频率加快,分子间作用力变得松弛和减弱[10],因此,温度较高时,偏离理想的程度会有所下降。

表3 DMF(1)-丙醇(2)二元系在不同温度下的黏度、过量黏度和过量流动活化自由能Table 3 Viscosities, excess viscosities and excess Gibbs energy of activation for viscous flow of DMF(1)-propanol(2) system from 288.15 K to 313.15 K
4个二元系的ΔG*E也均为负值,其偏差都随温度升高而减小。一般来说,负的ΔG*E主要归因于色散力和弱的偶极-偶极相互作用。过量流动活化自由能与体系中两组分间特殊的分子间相互作用有关,即说明有稳定的溶剂-助溶剂加合物形成。随温度升高,参与形成加合物的分子间相互作用减弱,而氢键和偶极的交叉网络结构对形成加合物的作用也明显下降。因此,温度越高,偏离理想的程度就越低。图5是4个体系298.15 K时的ΔG*E随组成变化的比较。发生最大偏差时溶液组成不同,DMF-乙醇约在x1=0.3处,DMF-丙醇约在x1=0.4,而DMF-EG和DMF-12PD体系约在x1=0.5附近。
过量黏度Δη采用Redlich-Kister方程进行关联

式中,x1为 DMF的摩尔分数,Bi为多元回归系数。关联结果的标准偏差δ用式(4)计算


表4 DMF(1)-乙二醇(2)二元系在不同温度下的黏度、过量黏度和过量流动活化自由能Table 4 Viscosities, excess viscosities and excess Gibbs energy of activation for viscous flow of DMF(1)-EG(2) system from 288.15 K to 313.15 K
式中,Δηexp和Δηcal分别代表过量黏度的实验值和计算值,Nexp为实验点个数,m为Redlich-Kister方程拟合参数个数。方程参数和标准偏差均列于表6。
2.2 二元系黏度的关联与预测
为预测二元系任一组成下的黏度,拟用下列半经验的黏度方程对实验数据进行关联[26-27]。
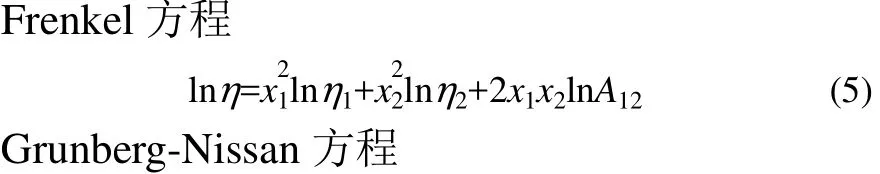

式(5)~式(8)中,η为混合液动力黏度,ν为混合液运动黏度,M为摩尔质量,x为摩尔分数,V为混合液摩尔体积,A12,G12,Wvis,Z12,Z21分别是各黏度方程的调节参数。下角标1和2分别表示组分1和组分2的相应性质。

表5 DMF(1)- 1,2-丙二醇(2)二元系在不同温度下的黏度、过量黏度和过量流动活化自由能Table 5 Viscosities, excess viscosities and excess Gibbs energy of activation for viscous flow of DMF(1)-12PD(2) system from 288.15 K to 313.15 K
相对标准偏差d

式中,n是实验数据点个数,p是黏度模型中调节参数个数,ηexp和ηcal分别代表黏度实验值和计算值。关联结果见表7。4个黏度模型的相对标准偏差几乎均小于 5%,其中三元体相互作用模型McAllister方程的预测结果最佳,对DMF和一元醇体系预测结果的平均相对标准偏差仅约 0.5%,对DMF和二元醇体系的平均偏差为1%左右。对于含醇二元液体混合物,分子间的相互作用相当复杂。活化流动过程中,一个分子越过势垒与不同组分的分子作用,并随局部浓度而改变,活化分子在分子层之间跃迁时经历着不同类型的相互作用。因此,建立在二维多元体相互作用模型上的McAllister方程能更准确地解释不同类型的相互作用对混合物活化自由能的贡献。

图1 不同温度下DMF(1)-乙醇(2)二元系的Δη-x1图Fig.1 Plot of Δη against x1 for DMF(1)-EtOH(2) binary mixture at different temperature

图2 不同温度下DMF(1)-丙醇(2)二元系的Δη-x1图Fig.2 Plot of Δη against x1 for DMF(1)-PrOH(2) binary mixture at different temperature
2.3 流动活化态的热力学性质
流动活化自由能ΔG*可通过Eyring黏度方程计算[28]

式中,h为Planck常数,N为Avogadro常数,V为摩尔体积。
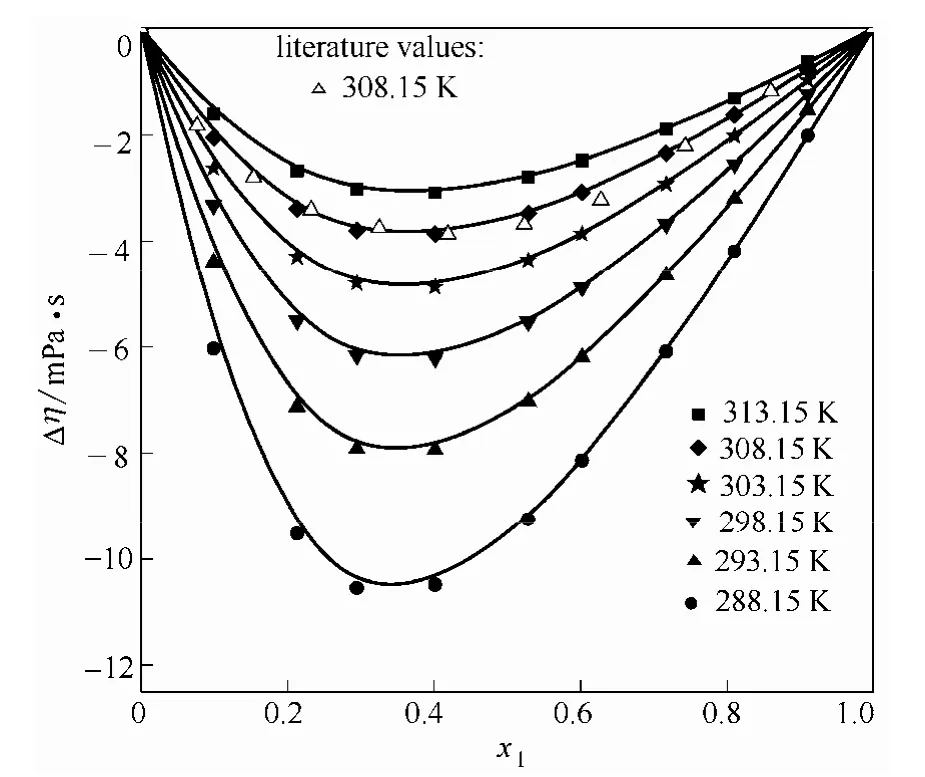
图3 不同温度下DMF(1)-乙二醇(2)二元系的Δη-x1图Fig.3 Plot of Δη against x1 for DMF(1)-EG(2) binary mixture at different temperature

图4 不同温度下DMF(1)-12PD(2)二元系的Δη-x1图Fig.4 Plot of Δη against x1 for DMF(1)-12PD(2) binary mixture at different temperature
流动活化自由能ΔG*的物理意义表示一个分子从基态到运动过渡态的能量势垒。从分子热力学和Eyring的黏度理论可知,热力学和传递性质的过量能量,都来源于混合过程中分子间相互作用力的变化,也就是分子间势垒的变化。正是由于分子间作用力在混合过程中的变化,使得表征溶液非理想性的过量热力学函数和溶液传递性质之一的黏度相联系。结合热力学关系式ΔG*=ΔH*-TΔS*可导出


图5 298.15 K时各体系的ΔG*E-x1图Fig.5 Plot of ΔG*E against x1 for binary mixtures at 298.15 K

表6 过量黏度的Redlich-Kister方程系数及标准偏差Table 6 Coefficients of Redlich-Kister equation and standard deviations for excess viscosities (Δη/mPa·s )
ΔH*和 ΔS*分别为流动活化焓和活化熵。以Rln(ηV/hN)对1/T作图,发现4个二元系均有良好的线性关系(相关系数达 0.99),这说明实验温度范围内组成一定时流动活化焓和活化熵为定值。从直线斜率和截距求出ΔH*和 ΔS*,列于表8。
4个体系的ΔG*和ΔH*都是正值,ΔS*在DMF-乙醇中为负值,其他3个体系中随x1(DMF摩尔分数)的增加,由正值变为负值。较小的活化熵值表明ΔG*主要是由焓效应决定。流动活化自由能 ΔG*随x1的增加,DMF-乙醇体系呈现“U”形曲线,而其他3个二元系均为单调下降。说明DMF-乙醇混合过程中流体活化态的形成在x1=0.35处最容易,而另3个体系在富DMF区更容易[29]。
一元醇的ΔS*都较小,少量的DMF的介入即导致 ΔS*由正值变为负值,说明混合过程中形成的流动活化物具有较高的有序性。而二元醇混合物中当x1=0.7以上时ΔS*才变为负值。DMF分子结构说明,在DMF分子中的氧原子是负极性的,是最好的氢键受体。由于这些负电荷的孤电子对的完全暴露,DMF分子会被非常强地溶剂化。另一方面,由于两个电子排斥基团—CH3的存在,使得正极性的氮原子上的孤对电子具有更加明显的给体倾向[24]。当与醇混合时,能与醇分子中的羟基形成不同类型的氢键。醇是高度结构化的液体,一元醇分子通过羟基上的氢键发生自缔合,二元醇分子可以通过分子间和分子内的氢键发生自缔合,而这些分子内氢键会非常大地影响分子间氢键的形成。因此,烷基二元醇中能与 DMF分子缔合的羟基比例比一元烷醇中要低,这导致不同种分子间的氢键明显减少[30],形成的流动活化态结构性略低。
3 结 论
(1)常压下测定了DMF分别与乙醇、丙醇、乙二醇和 1,2-丙二醇形成的二元系在 288.15~313.15 K下全浓度范围内的黏度, 由实验数据计算了过量黏度和过量流动活化自由能。4个二元系的过量黏度和过量流动活化自由能均为负值,并都随温度降低而偏差增大。过量黏度最低值均发生在DMF摩尔分数约为0.3处。
(2)半经验的黏度模型:Frenkel方程、Grunberg-Nissan方程、Katti-Chaudhari方程和McAllister方程对实验数据的关联结果表明,均适用于对混合物黏度的预测,其中 McAllister模型的关联结果最好,预测值与实验值的平均相对偏差最小。
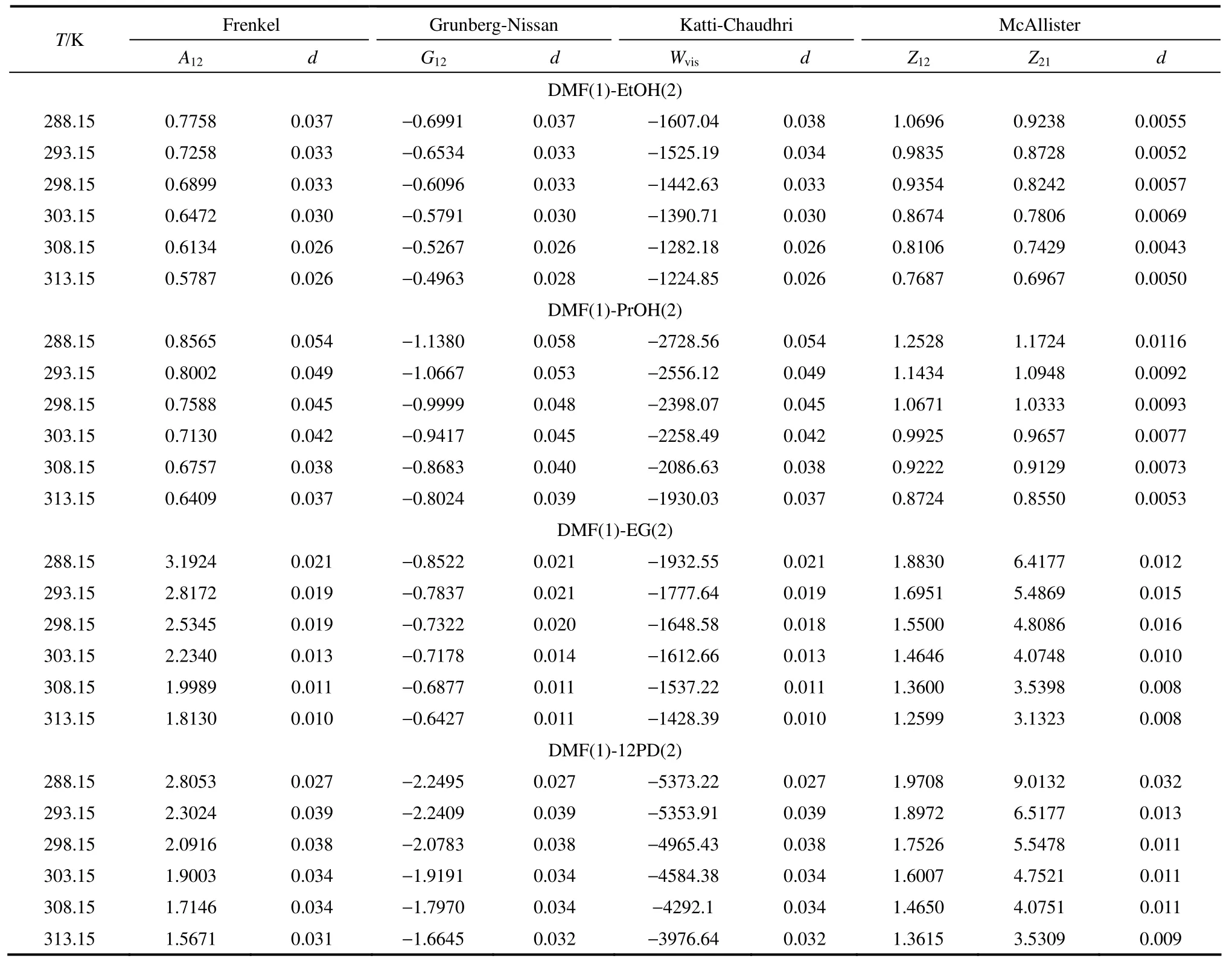
表7 不同温度下4个半经验方程的调节参数和相对标准偏差Table 7 Adjustable parameters and standard deviation of four semi-empirical equations at different temperatures
(3)流动活化自由能 ΔG*和活化焓 ΔH*均为正值,而活化熵 ΔS*随 DMF组分增加由正值变为负值。
致谢:感谢湖州师范学院2017年大学生创新创业科研训练项目的资助。
符 号 说 明
A12——Frenkel方程调节参数
Bi——Redlich-Kister方程拟合参数
d——相对标准偏差
G12——Grunberg-Nissan方程调节参数
ΔG*——流动活化自由能,kJ⋅mol-1
ΔG*E——过量流动活化自由能,J⋅mol-1
ΔH*——流动活化焓,kJ⋅mol-1
M——摩尔质量,g⋅mol-1
ΔS*——流动活化熵,J·K-1·mol-1
V——摩尔体积,cm3·mol-1
Wvis——Katti-Chaudhari方程调节参数
x1——N,N-二甲基甲酰胺的摩尔分数
Z12,Z21——McAllister方程调节参数
δ——Redlich-Kister方程标准偏差
η——黏度,mPa·s
Δη——黏度偏差,mPa·s
ρ——密度,g·cm-3
下角标
1——组分1
2——组分2

表8 流动活化自由能、活化焓和活化熵Table 8 Values of free energy (ΔG*) enthalpy (ΔH*) and entropy (ΔS*) of activation of viscous flow
[1] LAN G J, XU Q X, SUN S Y, et al. Thermodynamic properties and spectral investigation of dilute sulfur dioxide in binary system N,N-dimethylformamide + diethylene glycol[J]. Fluid Phase Equilibria, 2015, 389: 74-82.
[2] ZAREI H, GOLROUDBARI S A, BEHROOZI M. Experimental studies on volumetric and viscometric properties of binary and ternary mixtures of N,N-dimethylacetamide, N-methylformamide and propane-1,2-diol at different temperatures[J]. Journal of Molecular Liquids, 2013, 187: 260-265.
[3] UDDIN M H, KHAN M Z H, RAHMAN M H, et al. Volumetric and viscometric properties observed for the mixtures of DMF(N,N-dimethyl formamide) and other alcohols (butanol and 1-propanol)[J]. Physics and Chemistry of Liquids, 2014, 52(2):251-261.
[4] BHUIYAN M M H, UDDIN M H. Excess molar volumes and excess viscosities for mixtures of N,N-dimethylformamide with methanol,ethanol and 2-propanol at different temperatures[J]. Journal of Molecular Liquids, 2008, 138: 139-146.
[5] YANG C S, SUN Y, HE Y F, et al. Volumetric properties and viscosities of binary mixtures of N,N-dimethylformamide with methanol and ethanol in the temperature range (293.15 to 333.15)K[J]. J. Chem. Eng. Data, 2008, 53(1): 293-297.
[6] 张蓉蓉, 窦茂斌, 袁恩先, 等. 均三甲苯/二异丁基甲醇混合溶剂黏度测定及关联[J]. 化工学报, 2015, 66(9): 3377-3382.ZHANG R R, DOU M B, YUAN E X, et al. Measurement and correlation of viscosities of mixed solvents 1,3,5-trimethylbenzene and diisobutylcarbinol[J]. CIESC Journal, 2015, 66(9): 3377-3382.
[7] ALMASI M. Densities and viscosities of the mixtures (formamide +2-alkanol): experimental and theoretical approaches[J]. J. Chem.Thermodynamics, 2014, 69: 101-106.
[8] KONDAIAH M, SREEKANTH K, SRAVANA KUMAR D, et al.Densities, viscosities, and excess properties for binary mixtures of ethylene glycol with amide at 308.15 K[J]. J. Therm. Anal. Calorim.,2014, 118: 475-483.
[9] MOOSAVI M, MOTAHARI A, OMRANI A, et al. Thermodynamic study on some alkanediol solutions: measurement and modeling[J].Thermochimica Acta, 2013, 561: 1-13.
[10] MANFREDINI M, MARCHETTI A, SIGHINOLFI S, et al.Kinematic viscosities of binary liquid mixtures of 2-butanone with 1,2-propanediol[J]. Journal of Solution Chemistry, 2002, 31(3):235-252.
[11] NAIN A K. Densities and volumetric properties of (formamide +ethanol, or 1-propanol, or 1,2-ethanediol, or 1,2-propanediol)mixtures at temperatures between 293.15 K and 318.15 K[J]. J. Chem.Thermodynamics, 2007, 39: 462-473.
[12] ZEMANKOVA K, TRONCOSO J, ROMANI L. Excess volumes and excess heat capacities for alkanediol + water systems in the temperature interval (283.15—313.15 K)[J]. Fluid Phase Equilibria,2013, 356: 1-10.
[13] ZIVKOVIC E M, KIJEVCANIN M L, RADOVIC I R,et al.Viscosities and refractive indices of binary systems acetone +1-propanol, acetone + 1,2-propanediol and acetone + 1,3-propanediol[J]. Chem. Ind. Chem. Eng. Q., 2014, 20(3): 441-455.
[14] JÓŹWIAK M, TYCZYŃSKA M, BALD A. The physicochemical properties and viscosity behavior of crown ether 18C6 in the mixture of water withN,N-dimethylformamide[J]. Journal of Molecular liquids, 2017, 229: 520-529.
[15] BENNETT V, DIKIO C W, ANGAYE S S,et al.Interaction of 1-butyl-3-methylimidazolium hexafluorophate withN,N-dimethylformamide:density and viscosity measurements[J]. Journal of Molecular Liquids,2016, 219: 661-666.
[16] HASSEIN-BEY-LAROUCI A, IGOUJILEN O, AITKACI A,et al.Dynamic and kinematic viscosities, excess volumes and excess Gibbs energies of activation flow in the ternary mixture 1-propanol +N,N-dimethylformamide + chloroform at temperatures between 293.15 K and 323.15 K[J]. Thermochimica Acta, 2014, 589: 90-99.
[17] 李丹, 方文军, 刘莉, 等.N-甲基哌嗪与乙酸乙酯、乙酸丁酯二元混合体系在298.15~313.15 K的体积及黏度性质[J]. 高等学校化学学报, 2013, 34(8): 1924-1928.LI D, FANG W J, LIU L,et al. Volumetric and viscous properties for binary mixtures ofN-methylpiperazine with ethyl acetate or butyl acetate from 298.15 K to 313.15 K[J]. Chemical Journal of Chinese Universities, 2013, 34(8): 1924-1928.
[18] QIAO Y, YAN F Y, XIA S Q,et al. Densities and viscosities of 1-butyl-3-methylimidazolium hexafluorophosphate [bmim][PF6] +CO2binary system: determination and correlation[J]. Chinese Journal of Chemical Engineering, 2013, 21(11): 1284-1290.
[19] CHOUDHARY D S, LADOLE C A, ASWAR A S. Interaction of 5-chloro-2-hydroxy-3-nitroacetophenone inN,N-dimethylformamide at various temperatures: a viscometric, volumetric and ultrasonic study[J]. Proc. Natl. Acad. Sci., India, Sect. A Phys. Sci., 2015, 85(2):221-226.
[20] KESHAPOLLA D, GARDAS R L. Study on solvation behavior of benzyl methyl ammonium carboxylate ionic liquids inN,N-dimethylformamide by physicochemical properties[J]. J.Solution Chem., 2015, 44: 469-494.
[21] ALKHALDI K H A E, AL-JIMAZ A S, ALTUWAIM M S. Densities,ultrasonic speeds and refractive indices of phenetole withN-methyl-2-pyrrolidone,N,N-dimethylformamide and tetrahydrofuran binary mixtures at different temperatures[J]. J. Chem.Thermodynamics, 2016, 103: 249-256.
[22] NAIN A K. Densities, ultrasonic speeds, viscosities and excess properties of binary mixtures of methyl methacrylate withN,N-dimethylformamide andN,N-dimethylacetamide at different temperatures[J]. J. Chem. Thermodynamics, 2013, 60: 105-116.
[23] PANDARINATH S N, SANJEEVAN J K. Excess molar volumes and deviations in viscosity of binary mixtures ofN,N-dimethylformamide with aniline and benzonitrile at (298.15, 303.15, 308.15, and 313.15)K[J]. J. Chem. Eng. Data, 2003, 48: 972-976.
[24] VENKATESU P. Thermophysical contribution ofN,N-dimethylformamide in the molecular interactions with other solvents[J]. Fluid Phase Equilibria, 2010, 298: 173-191.
[25] SHOKOUHI M, JALILI A H, HOSSEINI-JENAB M,et al.Thermo-physical of aqueous solutions ofN,N-dimethylformamide[J].Journal of Molecular liquids, 2013, 186: 142-146.
[26] MOHAMMAD A A, ALKHALDI K H A E, ALTUWAIM M S,et al.Viscosity and surface tension of binary systems ofN,N-dimethylformamide with alkan-1-ols at different temperatures[J].J. Chem. Thermodynamics, 2013, 56: 106-113.
[27] MOHAMMAD A A, ALKHALDI K H A E, ALTUWAIM M S,et al.Effect temperature and chain length on the viscosity and surface tension of binary systems ofN,N-dimethylformamide with 1-octanol,1-nonanol and 1-decanol[J]. J. Chem. Thermodynamics, 2014, 74:7-15.
[28] NAIN A K. Ultrasonic and viscometric studies of molecular interaction in binary mixtures of formamide with ethanol, 1-propanol,1,2-ethanediol and 1,2-propanediol at different temperatures[J].Journal of Molecular Liquids, 2008, 140: 108-116.
[29] DAS D, SALHI H, DALLEL M,et al.Viscosity Arrhenius activation energy and derived partial molar properties in isobutyric acid+water binary mixtures near and far away from the critical temperature,302.15 to 313.15K[J]. J. Solution Chem., 2015, 44: 54-66.
[30] SANZ L F, GONZALEZ J A, FUENTE I G D L,et al.Thermodynamics of mixtures with strong negative deviation Raoult’s law (XIV): Density, permittivity, refractive index and viscosity data for the methanol + cyclohexylamine mixture at (293.15—303.15)K[J].Thermochimica Acta, 2016, 631: 18-27.
date:2017-04-26.
Prof. LING Jinlong, lingjinlong@zjhu.edu.cn
Measurement and correlation of viscosities of binary mixtures ofN,N-dimethylformamide with ethanol, propanol, ethylene glycol or 1,2-propanediol
LING Jinlong, WANG Junyi, HUANG Huibo, SUN Laiyu, LU Xinyue
(School of Life Sciences,Huzhou University,Huzhou313000,Zhejiang,China)
The viscosities of binary mixtures consisting of ethanol, propanol, ethylene glycol or 1,2-propanediol withN,N-dimethylformamide (DMF) were determined for the whole range of compositions at 288.15—313.15 K under atmospheric pressure by using Ubbelohde viscometer. The excess molar viscosity (Δη) and excess Gibbs energy of activation of viscous flow (ΔG*E) were calculated from the experimental data, and correlated by Redlich-Kister equation. The viscosities of binary mixtures were correlated and predicted with four different expressions (Frenkel, Grunberg-Nissan, Katti-Chaudhari and McAllister model). It has been using the theory of Eyring method to calculate the thermodynamic functions of activation of viscous flow, such as the flow activation free energy, the activation enthalpy and entropy. The results show that both Δηand ΔG*Eare negative over the whole mole fraction range in the temperature range studied for all of the binary mixtures, and the deviation is greater as temperature decreases. All the viscosity deviations reached the minimum values atx1(DMF)≈0.3. The three-body McAllister semi-empirical equation was found to be the best correlation to represent the viscosities of all binary mixtures, in which the average relative errors between predicted and experimental data were minimum.The differences of intermolecular interaction between monohydric and dibasic alcohol with DMF were compared and analyzed.
N,N-dimethylformamide; viscosity; excess molar viscosity; excess Gibbs energy of activation of viscous flow; activation enthalpy; activation entropy
O 642
A
0438—1157(2017)11—4043—11
10.11949/j.issn.0438-1157.20170475
2017-04-26收到初稿,2017-07-28收到修改稿。
联系人及第一作者:凌锦龙(1964—),男,副教授。
