基于非线性渐进损伤模型的复合材料波纹梁耐撞性能研究

蒋宏勇， 任毅如， 袁秀良， 高宾华

湖南大学 机械与运载工程学院， 长沙 410082

基于非线性渐进损伤模型的复合材料波纹梁耐撞性能研究

蒋宏勇， 任毅如*， 袁秀良， 高宾华

湖南大学 机械与运载工程学院， 长沙 410082

基于连续介质损伤力学，提出了一种包括层内和层间失效的非线性渐进损伤模型来预测复合材料波纹梁在轴向冲击下的失效行为。其中，层内损伤采用最大应力准则，并结合指数型损伤演化法则和刚度折减方法预测失效后的材料参数。层间损伤模型则采用了二次名义应力准则、基于混合模式能量的指数型损伤演化法则和黏性刚度折减方法建立。基于该模型，对典型的波纹梁结构参数和触发等对耐撞性的影响进行了研究。结果表明数值模拟结果与试验结果基本吻合，模型能够准确地模拟复合材料波纹梁在冲击过程中出现的分层、纤维和基体破坏等失效模式。波纹梁在破坏过程中吸收的能量、比吸能和载荷峰值随层数不断递增，降低高度和减小触发结构的截面面积均会降低载荷峰值。

复合材料； 波纹梁； 损伤模型； 耐撞性； 层内和层间失效

耐撞性是指飞行器结构在发生可生还坠撞过程中具有的保护乘员安全的一种能力。随着航空技术的不断提高，全球航空事故的发生率在近几十年一直处于较低水平，且呈下降趋势，但是由于飞行次数的不断增加，航空事故总数并没有明显地减少。造成飞行器发生空难的意外因素较多，典型的如鸟撞、其他物体撞击导致的机械故障和恶劣气候条件等外在因素，还有发动机和操作系统等技术问题，使得航空事故始终无法避免。因此合理的耐撞性结构设计对航空安全具有重要意义。

由于复合材料相对传统的金属材料具有比强度高、比刚度大、吸能效率高和质量轻等优点，因此在吸能结构的设计中逐渐取代了金属材料，并且被广泛地应用于飞行器的抗坠毁设计中。为了提高复合材料结构的耐撞性，各国学者对铺层顺序、受载方式、几何特征以及薄弱环节等对复合材料结构耐撞性的影响进行了研究[1-4]。包括方管、圆管、波纹管和蜂窝结构等在内的高效薄壁吸能结构被广泛研究[5-13]。虽然已开展了大量研究，但复合材料在破坏过程中具有纤维和基体破坏等复杂的破坏模式，且均采用唯象的强度理论，无法准确地预测破坏过程，因此需对复合材料吸能结构的破坏模型展开更深入的研究。

波纹梁结构具有吸能效率高等优点，在航空航天、汽车等工程结构的耐撞性设计中被广泛应用。为提高复合材料波纹梁结构的耐撞性，国内外研究者对复合材料波纹梁进行了深入研究。Feraboli[14]对不同复合材料波纹试样进行轴向压缩试验，并比较了不同波纹试样的吸能能力，结果表明大波浪或半圆形截面的波纹梁的吸能能力最高。龚俊杰和王鑫伟[15]采用理想弹塑性材料来等效模拟复合材料波纹梁的破坏过程和吸能能力，并进一步根据等效原则分析了薄弱环节对波纹梁峰值载荷的影响，得出的结果与试验结果比较接近，但该等效参数的方法忽略了复合材料的各向异性，无法准确地模拟复合材料波纹梁的损伤形式。孟祥吉等[16]对复合材料波纹梁进行动态冲击试验，采用改进的Hashin失效准则和改进的损伤演化对波纹梁的冲击过程进行数值模拟，得到的结果与试验结果基本吻合，然后分析了薄弱环节设置对复合材料波纹梁吸能能力的影响。但上述方法忽略了复合材料的层间破坏模式和剪切力对基体压缩破坏的影响，因此无法准确地描述复合材料波纹梁的失效形式。Duan等[17]提出一种多目标粒子群优化算法对复合材料波纹梁的厚度和波纹半径进行优化，所采用的单壳模型，无法模拟分层问题。为了解决分层问题，并能够准确地模拟复合材料波纹梁的破坏过程，Sokolinsky[18]采用具有层内与层间破坏的损伤模型，对复合材料波纹梁的准静态轴向压缩进行模拟，得到的载荷-位移曲线和损伤形貌与试验结果非常接近，但是研究内容缺乏各种影响参数的分析，并且采用的失效准则没有考虑剪切力对纤维和基体的影响。复合材料波纹梁在轴向冲击载荷下的破坏模式非常复杂，不仅存在层内损伤(基体挤裂、纤维断裂和纤维基体分离等)，还存在层间损伤(分层破坏)。目前，各种材料模型还无法准确地模拟复合材料波纹梁复杂的破坏模式。因此有必要对复合材料波纹梁的冲击动力学模型展开相关研究。

本论文提出了采用非线性渐进损伤模型来模拟编织复合材料波纹梁在准静态轴向冲击下的响应过程。该模型的层内损伤采用最大应力失效准则、指数型损伤演化[19]和刚度折减的方法。采用二次名义应力失效准则、基于混合模式能量法的指数型损伤演化和黏性刚度折减的方法建立了层间损伤模型[20-22]。基于该模型，对典型几何参数、铺层方法和触发结构等对波纹梁耐撞性的影响进行了分析。

1 复合材料非线性渐进损伤模型

复合材料呈各向异性，其破坏模式比各向同性材料更加复杂。复合材料波纹梁在冲击过程中，不仅通过层内破坏来耗散能量，层间破坏也将吸收部分能量。其中层内损伤模式有纤维拉伸断裂、纤维挤压破坏、基体开裂以及基体挤裂等，层间损伤模式为分层破坏。在损伤过程中，层内与层间损伤均采用刚度折减和指数型损伤演化的方法来模拟复合材料波纹梁的渐进损伤。

1.1 层内渐进损伤

基于连续介质损伤力学，采用损伤变量di可有效地描述复合材料层内的渐进损伤过程，采用非线性复合材料损伤模型来计算刚度矩阵折减系数[23]。各向异性复合材料损伤本构模型为

(1)

式中：σ11和σ22为正应力；σ12为剪切应力；ε11和ε22为正应变；ε12为剪切应变；C(di)为刚度矩阵函数，其中自变量为损伤变量di，其表达式为

(2)

式中：E为弹性模量；G为剪切模量；ν为泊松比；D为分层破坏损伤变量；ds为剪切损伤变量；df和dm分别为纤维和基体的损伤变量，且

(3)

其中：d为损伤变量，下标ft、fc、mt和mc分别表示纤维拉伸、纤维压缩、基体拉伸和基体压缩。

1.1.1 失效准则

基于最大应力失效准则，建立了一种可区分主要损伤模式的失效准则。该失效准则的各失效模式彼此独立，且仅与纤维与基体方向的拉压强度有关，如式(4)～式(7)所示。

(4)

(5)

(6)

(7)

(8)

损伤阈值(rft、rfc、rmt、rmc)通过历史损伤变量获得，且在损伤过程中会不断增大，其值取时间t内历史损伤变量的最值，即

(9)

式中：τ为时间变量；t为当前时刻。当rft、rfc、rmt、rmc中任何一个值大于或等于1时，材料将开始发生失效。

1.1.2 损伤演化

若损伤历史变量满足条件，那么材料点将开始发生失效，材料参数将根据材料折减模型进行更新。目前主要有3种材料参数折减模型：瞬间减小到0、减少到某一个恒定的值和按指定的路径逐渐减少[24]，如图1所示。

图1 材料属性的折减行为Fig.1 Properties degradation behavior of material

该模型采用按指定路径逐渐减少的指数型折减方案来模拟材料渐进损伤，即指数型损伤演化模型[19]。损伤变量的演化形式由式(10)～式(13)描述。

(10)

(12)

(13)

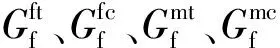
(14)

损伤变量dft、dfc、dmt、dmc的值均为0时，材料未失效；值在(0,1)之间时，材料未完全失效；值为1时，材料完全失效。4个损伤变量均单调递增，与有效应力的关系为

(15)

损伤演化由式(10)～式(13)来实现，并引入特征单元长度Lc和断裂能。Lc的引入保证了数值模拟有关网格密度的客观性；断裂能等于耗散能，耗散能会随着单元尺寸的减小而减小。因此将单元特征长度和能量耗散引入到损伤演化法则中可以减小对网格尺寸的敏感性。由于损伤变量为单调递增量，故单元的最大尺寸被限制，由式(16)推断。

α=ft,fc,mt,mc

(16)

若有限单元的特征长度超过Lmax，计算将过度预测耗散能。

剪切损伤的失效准则为

(17)

(18)

剪切损伤阈值r12取时间t内φ12的最值，即

(19)

(20)

1.2 层间渐进损伤

考虑分层破坏可更准确地模拟复合材料波纹梁的损伤模式。模拟复合材料分层破坏的数值方法有虚拟裂纹张合技术(VCCT)、界面单元以及基于表面的黏性接触等[20-21]。采用黏性接触的方法只需在层与层接触的表面定义黏性接触属性，且计算速度较快，故分层损伤模型采用基于表面的黏性接触的方法。

1.2.1 本构关系及失效准则

基于表面的黏性接触提供一种与界面单元相似的能力，均采用应力-位移准则[20]描述本构关系，如式(21)。

(21)

式中：tn为正应力；ts和tt为剪应力；kn为法向黏性刚度；ks和kt为2个切向黏性刚度；δn为法向相对位移；δs和δt为2个切向相对位移；t为应力矩阵；K为刚度矩阵；δ为位移矩阵。

分层损伤起始由二次名义应力失效准则[20]判定。当关于应力比的二次函数值到达1时，分层损伤开始，其失效准则为

(22)

1.2.2 损伤演化

为提高损伤演化的准确性，该模型采用指数型损伤演化[19]，由式(23)定义。

(23)

损伤未开始时，D=0；损伤开始后，D将不断增大到指定值，即完全损伤。损伤模型采用基于Benzeggagh-Kenane(BK)准则[20,22]的混合模式能量法来建立，如式(24)。

(24)

图2 应力-位移响应Fig.2 Traction-separation response

2 模型验证

2.1 有限元模型

基于ABAQUS/Explicit的有限元分析程序，层内材料属性的更新采用Fortran语言编写用户子程序VUMAT[20]来实现。主程序将对每个材料点调用子程序，在n+1个时间步中，计算过程如下：

1) 主程序将初始材料参数及应变增量Δεn+1传递到子程序中。

2) 计算材料点的应变εn+1=εn+Δεn+1。

3) 计算刚度矩阵C(dn)。

4) 计算应力σn+1=C(dn)εn+1。

7) 计算损伤阈值rn+1。

9) 通过损伤变量dn+1判断材料是否完全损伤。若材料完全损伤，单元自动被删除并结束计算，反之执行第10)步。

10) 更新折减后的刚度矩阵C(dn+1)。

11) 更新应力。

VUMAT流程图如图3所示。

图3 VUMAT流程图Fig.3 Flow chart of VUMAT

模型由波纹梁和上下两端的刚性板组成。波纹梁的顶部边缘与上端刚性板固定并静止不动，下端刚性板以恒定速度撞击波纹梁。复合材料波纹梁和刚性板的有限元模型分别采用连续壳单元(SC8R)和离散刚体单元(R3D4)建立。模型单元数共82 120个，其中波纹梁单元为81 992个，厚度方向单元每层1个，采用2D本构模型。连续壳单元不仅具有3D实体单元的几何特征，而且在运动学和本构行为上与传统壳单元类似[20]。因此采用连续壳单元能准确地建立多层复合材料模型，并能够有效地提高计算速度。模型采用通用接触算法，并给定摩擦系数防止波纹梁与刚性板之间的相对滑动，然后通过特殊属性分配方法采用Traction-Separation本构模型定义黏性接触来模拟分层失效，其中层间摩擦系数为0.3。复合材料波纹梁的有限元模型如图4所示。

图4 波纹梁的有限元模型Fig.4 Finite element model of corrugated beam

2.2 试 验

复合材料波纹梁试件为研究对象，其材料为碳纤维环-氧树脂基T700/2510 TORAYCA织物[18]。试件尺寸如下：宽为50.80 mm，高为76.2 mm；共8层，每层厚度均为0.25 mm，铺层方式为[0/90]2S；截面形状[14]由3个半径为6.35 mm 的半圆组成，其横截面示意图如图5所示。为促使试件在压溃过程中被稳定地破坏，试件下端被加工成45° 倒角来触发。

复合材料波纹梁的冲击试验如图6所示[14]。冲击试验中，波纹梁试件被垂直固定于装置中的上下刚性表面之间，上端刚性冲击板可沿垂直固定于下端刚性板上的圆柱上下滑动。刚性球同上端刚性板以0.2 mm/s的准静态轴向冲击速度匀速压溃波纹梁试件。被压溃的波纹梁试件如图7所示[18]。根据试验现象，被压溃的波纹梁出现了基体破坏、纤维破坏、基体碎片飞溅以及被压溃的材料向两侧分离的分层现象。在压溃过程中，载荷峰值为18.327 kN，吸收的能量为504.92 J，比吸能最终为88.5 J/g。

图5 波纹梁的横截面示意图Fig.5 Schematic of cross-section of corrugated beam

图6 复合材料波纹梁的冲击试验Fig.6 Impact test of composite corrugated beam

图7 被压溃的波纹梁试件Fig.7 Crushed corrugated beam specimen

2.3 材料参数

表1 材料及损伤参数[18,25]Table 1 Material and damage parameters[18,25]

2.4 结果与讨论

为了验证损伤模型的正确性，对复合材料波纹梁在准静态轴向冲击载荷下得到的破坏模式、冲击过程、冲击载荷以及吸能特性进行分析。

2.4.1 破坏模式及冲击过程

如图8和图9所示，根据波纹梁在数值模拟过程中的破坏现象，压溃过程非常稳定，图9中s为压溃距离。层内损伤按定义的损伤模型发展，下端基体发生挤裂破坏，并产生大量飞溅的基体碎片。基于表面的黏性接触使波纹梁下端被破坏的区域出现明显的分层现象。波纹梁下端被破坏的区域以第3层和第4层为中心向两侧分离。复合材料波纹梁在冲击过程中出现的基体破坏、纤维断裂、基体碎片以及分层破坏等破坏模式与试验现象非常接近。

2.4.2 冲击载荷和吸能特性

图8 波纹梁的变形图Fig.8 Deformed shapes of corrugated beam

图9 波纹梁的冲击过程Fig.9 Impact process of corrugated beam

数值模拟与试验的载荷-位移曲线对比如图10 所示。数值模拟结果与试验结果基本吻合，其载荷-位移曲线在整个冲击过程中相对稳定，但在冲击的初始阶段出现了较高的载荷峰值，这与试验结果存在较小的差异。由于波纹梁在压溃过程中吸收的能量主要来自于稳定压溃阶段，且载荷峰值对应的能量吸收只占总能量吸收的小部分，因此较小的载荷峰值差异对研究结果影响较小。

比吸能(SEA)指单位质量吸收的能量，是评定结构吸能性能的重要指标，其计算公式为

(25)

图10 数值模拟与试验载荷-位移曲线对比 Fig. 10 Comparison of load-displacement curves for numerical simulation and test

式中：m为结构损伤部分的质量；h为结构有效压溃位移；x为破坏的长度；F为载荷；EA为吸收的能量。由式(25)可知，数值模拟和试验的比吸能误差与吸收的能量误差相等。

表2为数值模拟与试验得到的峰值载荷、吸收的能量EA和比吸能SEA。吸能曲线如图11所示，横坐标为有效压溃位移。有效压溃距离在12.5 mm以内时，数值模拟与试验的能量曲线非常接近；此后数值模拟的能量曲线相对试验偏低。由于对层与层间的摩擦系数和初始分层损伤参数进行了调整，因此导致了数值模拟的平均载荷偏低，进而造成能量曲线偏低。但相对误差仅为4.6%，因此能量曲线的偏低对模型验证的影响较小。根据对数值模拟与试验的数值结果和破坏模式等的分析，验证了该有限元模型的正确性。

表2数值模拟与试验得到的峰值载荷、EA和SEA

Table2Peakload,EAandSEAobtainedbynumericalsimulationandtest

MethodPeakload/kNEA/JSEA/(J·g-1)Test18．327504．9288．5Simulation23．131481．8184．4Error/%26．2-4．6-4．6

Notes: EA——Energy Absorption; SEA——Specific Energy Absorption.

图11 数值模拟与试验的吸能曲线对比
Fig.11 Comparison of absorbed energy curves for numerical simulation and test

3 复合材料波纹梁的冲击动力学性能

为了获得复合材料波纹梁的冲击动力学特性，分别对复合材料波纹梁的层数、高度、触发角度和触发类型对耐撞性的影响进行分析。

3.1 层数对耐撞性的影响分析

波纹梁厚度对波纹梁的耐撞性有较大影响[17]。由于波纹梁层数的变化会导致厚度发生变化，因此将对波纹梁的层数进行研究。分别对4层、6层和8层的复合材料波纹梁进行研究，其中波纹梁每层厚度为0.25 mm，铺层方式分别为[0/90]S、[0/90]3、[0/90]2S。各层数所对应的载荷-位移曲线如图12所示，4层波纹梁所对应的峰值载荷、吸收的能量和比吸能相对8层的分别减少了40.8%、57.0%、16.4%。6层波纹梁所对应的峰值载荷、吸收的能量和比吸能相对8层的分别减少了20.0%、33.5%、13.8%。

图12 层数对耐撞性的影响Fig.12 Effect of numbers of layers on crashworthiness

由此可知，波纹梁在冲击过程中的峰值载荷、吸收的能量和比吸能随层数不断递增。由于层数的增加会引起波纹梁厚度的增加，使波纹梁与刚性板接触的承载面积增大，并导致平均载荷增大，因此最终影响吸收的能量。

3.2 高度对耐撞性的影响分析

高度是波纹梁结构典型的设计参数。为了研究波纹梁在破坏模式接近时的高度对波纹梁耐撞性的影响，分别对高度为 36.1、56.6 和 76.2 mm 的复合材料波纹梁进行分析。图13为不同高度所对应的载荷-位移曲线。当高度为36.1 mm时，相对76.2 mm所对应的载荷峰值降低了9.5%，吸收的能量和比吸能降低了4.4%。当高度为56.6 mm时，相对76.2 mm所对应的载荷峰值降低了1.4%，吸收的能量和比吸能降低了3.7%。上述结果表明，波纹梁在冲击过程中的峰值载荷随高度的增加不断递增；吸收的能量和比吸能的误差较小，均在0%～4%之间。不同高度的波纹梁在冲击过程中出现的破坏模式接近时，高度对波纹梁耐撞性的影响较小。

图13 高度对耐撞性的影响Fig.13 Effect of heights on crashworthiness

3.3 触发角度对耐撞性的影响分析

触发角度指波纹梁底端触发斜面与水平的夹角。峰值载荷偏高会导致结构破坏失稳，并大幅度减少结构的吸能效率。为了降低波纹梁在冲击过程中的峰值载荷，分别对触发角度为30°、45° 和60° 的复合材料波纹梁进行研究。3种不同触发角度的结构示意图与其所对应的载荷-位移曲线分别如图14和图15所示。当触发角度为30° 和45° 时，所对应的载荷峰值相对较高，且载荷值均在23 kN左右。60° 触发角所对应的载荷峰值约为20 kN，相对45° 触发角降低了11.9%。

由此可知，较小的触发角度所对应的峰值载荷较高，60°触发角所对应的载荷峰值最低。各触发角度所对应的能量吸收和比吸能误差相对较小，因此触发角度对能量吸收和比吸能的影响也较小。

图14 3种不同触发角度的结构示意图Fig.14 Schematic of three different angles of trigger

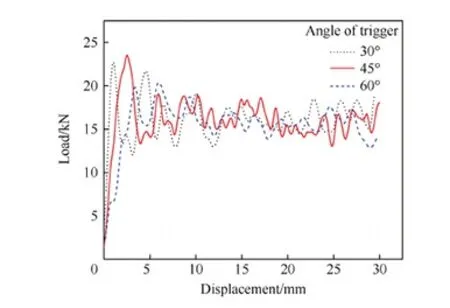
图15 触发角度对耐撞性的影响Fig.15 Effect of angles of trigger on crashworthiness

3.4 触发类型对耐撞性的影响分析

不同薄弱环节的设置对结构在冲击过程中的峰值载荷有较大影响[26]。为了进一步降低波纹梁在冲击过程中的峰值载荷，提出了复合材料波纹梁的几种触发类型，并对其进行分析。如图16所示，4种触发分别为:倒角形、W形、楔形和锯齿形；均基于45° 斜角。4种不同触发类型所对应的载荷-位移曲线和4种触发类型所对应的比吸能和吸收的能量分别如图17和18所示。

如图17所示：① W形与楔形触发的峰值载荷误差较小，其原因在于W形与楔形在等距离压溃时波纹梁与刚性板接触截面的承载面积相同(即虚线总长度相同)；相同的触发高度使载荷达到峰值的时间相同。② 锯齿形与W形、楔形的载荷峰值误差较小，但与倒角形的误差较大，高达32.5%。在等距离压溃时，锯齿形的截面承载面积分别是倒角形的4倍，W形与楔形的2倍，由于截面承载面积增大会导致载荷增大，因此锯齿形对应的载荷峰值较高。③ 如图17所示，可观察到锯齿形所对应的载荷-位移曲线有较大的震荡，导致稳定性较差。压溃至6 mm时，曲线出现了较低的载荷，但压溃至10 mm时，曲线逐渐趋于稳定。由于锯齿形所对应的载荷峰值较高，使得破坏过程的稳定性难以控制，较高的峰值会使薄弱环节区域瞬间损伤，导致波纹梁承载能力显著降低，随后出现较低的载荷，因此形成了较大的震荡。但该阶段过后(12.5 mm后)，波纹梁的破坏过程将逐渐稳定。

图16 4种不同触发的结构示意图Fig.16 Structure schematic of four different triggers

图17 触发类型对耐撞性的影响Fig.17 Effect of types of trigger on crashworthiness

图18 4种触发类型所对应的吸收能量和比吸能Fig.18 Four types of trigger corresponding to EA and SEA

上述分析表明，载荷峰值随触发截面承载面积的增大而增大。如图18所示，不同触发类型对吸收的能量和比吸能的影响相对较小。

4 结 论

采用连续介质损伤力学，建立非线性渐进损伤模型来模拟复合材料波纹梁在冲击过程中的损伤过程。基于准确的损伤模型，对典型的波纹梁设计参数和触发结构等对耐撞性的影响进行了分析。主要结论如下：

1) 层内与层间损伤分别采用最大应力失效准则、二次名义应力失效准则，均结合指数型损伤演化和刚度折减的方法准确地模拟了复合材料波纹梁层内和层间的渐进损伤过程。根据波纹梁的损伤形貌，得出复合材料波纹梁在冲击过程中出现的基体破坏、纤维断裂以及分层破坏等破坏模式与试验现象非常接近。

2) 波纹梁吸收的能量、比吸能和载荷峰值随层数不断递增，60° 触发角对应的载荷峰值最低，降低高度和减小触发结构的截面面积会降低载荷峰值。

[1] HAMADA H, RAMAKRISHNA S, SATO H. Effect of fiber orientation on the energy absorption capability of carbon fiber/PEEK composite tubes[J]. Journal of Composite Materials, 1996, 30(8): 947-963.

[2] 陈永刚, 益小苏, 许亚洪, 等. Carbon-Epoxy圆管件的静态吸能特征[J]. 航空学报, 2005, 26(2): 246-249.

CHEN Y G, YI X S, XU Y H, et al. Static energy absorption characteristics of carbon-epoxy tubes[J]. Acta Aeronautica et Astronautica Sinica, 2005, 26(2): 246-249 (in Chinese).

[3] HANAGUD S, CRAIG J I, SRIRAM P, et al. Energy absorption behavior of graphite epoxy composite sine webs[J]. Journal of Composite Materials, 1989, 23(5): 448-459.

[4] FARLEY G L. Effects of crushing speed on the energy-absorption capability of composite tubes[J]. Journal of Composite Materials, 1991, 25(10): 1314-1329.

[5] 任毅如, 向锦武, 罗漳平, 等. 飞行器机身结构耐撞性分析与设计[J]. 工程力学, 2013, 30(10): 296-304.

REN Y R, XIANG J W, LUO Z P, et al. Crashworthiness analysis and design of aircraft fuselage structure[J]. Engineering Mechanics, 2013, 30(10): 296-304 (in Chinese).

[6] 刘小川, 郭军, 孙侠生, 等. 民机机身段和舱内设施坠撞试验及结构适坠性评估[J]. 航空学报, 2013, 34(9): 2130-2140.

LIU X C, GUO J, SUN X S, et al. Drop test and structure crashworthiness evaluation of civil airplane fuselage section with cabin interiors[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(9): 2130-2140 (in Chinese).

[7] 任毅如, 向锦武, 罗漳平, 等. 客舱地板斜撑杆对民机典型机身段耐撞性能的影响[J]. 航空学报, 2010, 31(2): 271-276.

REN Y R, XIANG J W, LUO Z P, et al. Effect of cabin-floor oblique strut on crashworthiness of typical civil aircraft fuselage section[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(2): 271-276 (in Chinese).

[8] MAMALIS A G, MANOLAKOS D E, IOANNIDIS M B, et al. The static and dynamic axial collapse of CFRP square tubes: Finite element modelling[J]. Composite Structures, 2006, 74(2): 213-225.

[9] ZHANG P, GUI L J, FAN Z J, et al. Finite element modeling of the quasi-static axial crushing of braided composite tubes[J]. Computational Materials Science, 2013, 73(6): 146-153.

[10] 万志敏, 桂良进, 谢志民, 等. 玻璃-环氧圆柱壳吸能特性的试验研究[J]. 复合材料学报, 1999,16(2): 15-20.

WAN Z M, GUI L J, XIE Z M, et al. Experimental study on energy-absorption properties of glass-epoxy cylindrical shells[J]. Acta Materiae Compositae Sinica, 1999, 16(2): 15-20 (in Chinese).

[11] MAHDI E, MOKHTAR A S, ASARI N A, et al. Nonlinear finite element analysis of axially crushed cotton fibre composite corrugated tubes[J]. Composite Structures, 2006, 75(1): 39-48.

[12] ATAOLLAHI S, TAHER S T, ESHKOOR R A, et al. Energy absorption and failure response of silk/epoxy composite square tubes: Experimental[J]. Composites Part B： Engineering, 2012, 43(2): 542-548.

[13] SHI Q H, DAI D, CAO Z H. Tensile failure strength analysis and experimental confirmation of stitch reinforced composite of T-stiffened structure[J]. Polymers & Polymer Composites, 2012, 20(3): 307-312.

[14] FERABOLI P. Development of a corrugated test specimen for composite materials energy absorption[J]. Journal of Composite Materials, 2008, 42(3): 229-256.

[15] 龚俊杰, 王鑫伟. 复合材料波纹梁吸能能力的数值模拟[J]. 航空学报, 2005, 26(3): 298-302.

GONG J J, WANG X W. Numerical simulation of energy absorption capability of composite waved beams [J]. Acta Aeronautica et Astronautica Sinica, 2005, 26(3): 298-302 (in Chinese).

[16] 孟祥吉, 燕瑛, 罗海波, 等. 复合材料波纹梁冲击试验与数值模拟[J]. 复合材料学报, 2015, 32(1): 196-203.

MENG X J, YAN Y, LUO H B, et al. Impact tests and numerical simulation of composite waved-beam[J]. Acta Materiae Compositae Sinica, 2015, 32(1): 196-203 (in Chinese).

[17] DUAN S Y, TAO Y R, HAN X, et al. Investigation on structure optimization of crashworthiness of fiber reinforced polymers materials[J]. Composites Part B： Engineering, 2014, 60(2): 471-478.

[18] SOKOLINSKY V S. Numerical simulation of the crushing process of a corrugated composite plate[J]. Composites Part A： Applied Science & Manufacturing, 2011, 42(9): 1119-1126.

[20] ABAQUS 6.13 analysis user’s manual[M]. Pairs: Dassault Systemes, 2013.

[21] BEUTH J L. Separation of crack extension modes in orthotropic delamination models[J]. International Journal of Fracture, 1996, 77(4): 305-321.

[22] KENANE M, BENZEGGAGH M L. Mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites under fatigue loading[J]. Composites Science & Technology, 1997, 57(5): 597-605.

[23] MATZENMILLER A, LUBLINER J, TAYLOR R L. A constitutive model for anisotropic damage in fiber-composites[J]. Mechanics of Materials, 1995, 20(2): 125-152.

[24] SLEIGHT D W. Progressive failure analysis methodology for laminated composite structures: NASA/TP-1999-209107[R]. Washington, D.C.: NASA, 1999: 1-25.

[25] PINHO S T, ROBINSON P, IANNUCCI L. Fracture toughness of the tensile and compressive fibre failure modes in laminated composites[J]. Composites Science & Technology, 2006, 66(13): 2069-2079.

[26] 龚俊杰, 王鑫伟. 薄弱环节对复合材料波纹梁吸能能力的影响[J]. 材料工程, 2006(5): 28-31.

GONG J J, WANG X W. Effect of trigger geometry on energy absorption of composite waved-beams[J]. Journal of Materials Engineering, 2006(5): 28-31 (in Chinese).

(责任编辑： 徐晓)

Crashworthiness of composite corrugated beam based onnonlinear progressive damage model

JIANGHongyong,RENYiru*,YUANXiuliang,GAOBinhua

CollegeofMechanicalandVehicleEngineering,HunanUniversity,Changsha410082,China

Based on continuum damage mechanics, a nonlinear progressive damage model including intra- and inter-laminar failures was presented to predict the failure behavior of composite corrugated beam under the axial crushing. The maximum stress criterion combined with exponential damage evolution laws and stiffness discount method were adopted to predict the material parameters of intra-laminar damage. The inter-laminar damage model was modeled by a quadratic nominal stress criterion, an exponential damage evolution law based on the mixed-mode energy and cohesive stiffness discount method. Based on this model, the effect of triggers and the typical parameters of corrugated beam structures on crashworthiness were investigated. The results of numerical simulation show basic agreement with the experimental data. The failure modes of delamination, fiber and matrix damage that appeared in the impact process of composite corrugated beam can be simulated accurately. During the damage of corrugated beam, absorbed energy， specific energy absorption as well as the peak load are the increasing function with respect to the layers. In addition, the peak load decreases with the decreasing of height and trigger-sectional area.

composites; corrugated beam; damage model; crashworthiness; intra- and inter-laminar failures

2016-08-29；Revised2016-10-19；Accepted2016-11-11；Publishedonline2017-01-091550

URL：www.cnki.net/kcms/detail/11.1929.V.20170109.1550.004.html

s：NationalNaturalScienceFoundationofChina(11402011);theFundamentalResearchFundsfortheCentralUniversities(201401390741)

2016-08-29；退修日期2016-10-19；录用日期2016-11-11； < class="emphasis_bold">网络出版时间

时间：2017-01-091550

www.cnki.net/kcms/detail/11.1929.V.20170109.1550.004.html

国家自然科学基金 (11402011); 中央高校基本科研业务费专项资金 (201401390741)

*

.E-mailrenyiru@hnu.edu.cn

蒋宏勇， 任毅如， 袁秀良， 等． 基于非线性渐进损伤模型的复合材料波纹梁耐撞性能研究J． 航空学报,2017,38(6):220717.JIANGHY,RENYR,YUANXL,etal.CrashworthinessofcompositecorrugatedbeambasedonnonlinearprogressivedamagemodelJ.ActaAeronauticaetAstronauticaSinica,2017,38(6):220717.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.220717

V414.8; TB332

A

1000-6893(2017)06-220717-13

*Correspondingauthor.E-mailrenyiru@hnu.edu.cn