狭缝高度对传热倍增及温度漂移特性的影响
2017-11-21包芸林泽鹏
包芸+林泽鹏
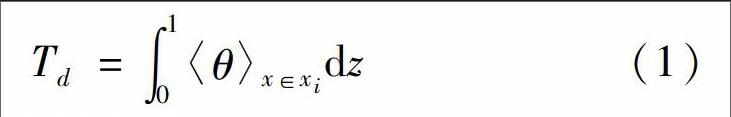
摘要: 为研究隔板对流装置的传热特性和温度漂移特性与系统几何尺寸的关系,采用DNS方法对不同狭缝高度和不同隔板数目的隔板对流装置进行计算,结果表明:传热通道中单向层流化的流动具有很好的二维性,二维与三维模拟计算得到相同的Nu。对多层隔板对流装置的传热倍增特性进行二维数值模拟发现:改变隔板顶端狭缝高度,传热倍增效果进一步增强;在隔板厚度相同时,不同隔板数的隔板对流装置存在一致的最优狭缝高度。定量研究传热通道的温度漂移量与狭缝高度的关系,发现二者存在标度律变化关系。
关键词: 隔板对流装置; 传热倍增; 狭缝高度; 温度漂移; 传热通道; Nu
中图分类号: O357.5 文献标志码: B
Effect of gap height on multiple enhancement of heat transfer and characteristics of temperature drift
BAO Yun, LIN Zepeng
(Department of Mechanics, Sun Yat-Sen University, Guangzhou 510275, China)
Abstract: In order to study the relationship between the characteristics of heat transfer and temperature drift of the partitioned convection device and the system geometrical dimensions, DNS method is used to calculate the partitioned convection device under different gap height and number of partitions. The results show that the unidirectional laminar flow in the heat transfer channel shows 2D character obviously, and the 2D sample shares an equal Nu with 3D sample. A 2D numerical simulation is performed to study the multiplication enhancement of heat transfer of partitioned convection device. The result shows that: the heat transfer efficiency can be enhanced further by changing the height of gaps; while the partitions thickness is equal, there is a coincident optimal gap height while the numbers of the partitions are different. The relationship between the temperature drift and heat transfer channel gap height is studied quantitatively, and it is found that there is a scaling relationship between them.
Key words: partition convection device; multiple enhancement of heat transfer; gap height; temperature drift; heat transfer channel; Nu
0 引 言
热对流现象在天体、地球地幔、大氣和海洋环流等自然界中广泛存在,在化工生产、核反应堆系统和电子元件设计等工程领域应用广泛。Rayleigh-Bénard(RB)热对流是热对流研究领域中最典型的流动物理模型之一,是当今物理学和流体力学研究领域的热门课题[1-2]之一,每年都有大量的有关RB对流传热特性的试验和数值模拟研究结果出现。如何增强对流装置的传热效率始终是热对流研究领域最重要的研究目标之一。使用粗糙导热板进行粗糙表面RB热对流特性研究[3-4],对转动RB热对流系统进行试验和数值模拟[5-7],平均温度接近流体沸点的研究[8],气泡成核热对流试验[9],不同厚度的方腔RB对流试验[10-11],在热对流系统的试验研究中加入聚合物粒子[12-13],以及不同宽高比的长方形对流装置分析[14-15]等多种RB热对流试验和数值计算研究发现,很多方法都可以有效增强热对流的传热效率。
BAO等[16]在宽高比为5的试验对流槽内等距加入竖直的隔板,在隔板的上下两端留出微小缝隙(该缝隙原本是为试验中保证只有一个注水孔可以注满整个装置而留的)。试验发现,随着隔板数增加,隔板对流装置的传热努塞尔数Nu明显增强,隔板数为6块时的增大幅度约为30%左右。对此现象开展数值模拟研究发现:不断增加隔板数量,隔板间的子单元会出现温度漂移现象,且流动从湍流状态向单向层流状态变化,会导致传热Nu进一步增加,隔板为28块时的Nu为没有加隔板时的Nu的2.3倍,传热增强130%,传热效率倍增。
计算对比研究发现,隔板数较多时,系统层流化后,隔板对流装置中的流动呈现出很好的二维性,二维流动和三维流动的传热Nu基本一致。因此,本文采用二维DNS数值模拟方法,研究有狭缝隔板热对流装置的传热特性,通过改变隔板对流装置中的隔板几何参数,研究系统传热效率与狭缝高度和隔板数之间的关系,以及传热通道的温度分布特性,并讨论传热通道中温度漂移特性与狭缝高度之间的关系。endprint
1 狭缝隔板热对流的数值计算
1.1 有狭缝RB隔板对流装置
在RB热对流装置内等距加入竖直隔板,在隔板的上下两端留出微小缝隙[16],见图1。定义隔板上下两端细小缝隙为横向流动的狭缝,隔板间的空腔为纵向传热通道(子对流单元)。狭缝的高度为d,隔板厚度即狭缝长度为l,隔板间的传热通道宽度为b,装置高度即传热通道长度为H,整个装置的宽度为D,整个装置的展向宽度为W。与试验对应,取隔板对流装置的宽高比Γ=5,隔板厚度l=0.12,Pr=5.3,Ra=108。
1.2 隔板对流装置传热流动的DNS数值模拟
在Boussinesq近似和不可压流动假设下,无量纲化后的二维热对流描述方程为
式中:Ra和Pr是对流系统的控制参数。隔板对流装置的四壁及隔板壁上的速度边界条件均为无滑移边界条件,侧壁和隔板壁为绝热条件,上壁温度(无量纲化)为恒温θ=0.5,下壁温度为θ=-0.5。三维热对流方程和边界条件与二维类似。
热对流DNS计算求解过程采用投影法[17],应用交错网格,空间采用二阶中心差分格式离散方程,时间为一阶的欧拉方法。在有狭缝隔板的多联通域中,压力泊松方程全场联立求解,不能采用直接求解方法。本文计算采用跳点迭代方法[18]求解压力泊松方程。大量方腔热对流流动的计算和结果对比验证认为本文计算的对流传热结果合理。[16]
RB热对流研究的核心问题之一是热量的传递现象,表征热量传递的物理参数是Nu。对无隔板的对流装置和隔板对流装置的热对流进行DNS模拟,探讨隔板对流装置的传热倍增现象及其物理特性。本文讨论的所有物理量均经过无量纲处理。
Γ=5,Ra=108,Pr=5.3时无隔板的对流装置二维计算的瞬时温度和速度分布见图2。无隔板时对流装置内有热羽流和冷羽流涌出[19],形成典型的有大尺度环流的湍流热对流。长时间计算得到平均场后,可求得在Γ=5,Ra=108,Pr=5.3时的热对流装置的传热Nu。湍流热对流的DNS计算结果显示,在二维计算时Nu=26.7,在三维计算时Nu=31.4,二维和三维计算得到的Nu结果不同。
Γ=5,Ra=108,Pr=5.3,l=0.12的20块隔板对流装置二维计算的温度和速度分布见图3。隔板间的子区形成较窄的传热通道,出现相间分布的温度漂移现象,热流在传热通道中形成单向层流,温度较高的通道中流动单向向上,温度较低的通道中流动单向向下,使得所有传热通道都为单向的传热流。有研究[20]表明传热通道内流动单向层流化会大大提高传热效率。正是这样的温度漂移现象和单向层流流动的冷流和热流,导致整个隔板传热装置的传热效率倍增。
实际流动装置是三维的,所以进行隔板对流装置的三维模拟计算,结果见图4。图4a)中的温度分布显示,三维结果与二维结果有同样的温度漂移现象。图4b)所示的横截面速度分布表明,隔板对流装置的流动形成单向层流流动后,由于隔板顶端二维狭缝的诱导作用,流动具有很好的二维性。三维模拟结果显示出的二維性,使得二维和三维计算得到的隔板对流装置的传热Nu基本相同。
三维计算采用的网格数为2 000×128×400,采用OpenMP并行方法在64核工作站上运行40 d完成计算;二维计算采用网格2 000×450,采用单核运行3 d完成计算:可见三维计算量远大于二维计算量。计算统计结果见表1。
在无隔板装置的湍流热对流情况下,二维和三维计算的传热Nu不同,三维计算的Nu要大于二维计算的Nu。加入隔板后,由于层流作用,20块隔板和28块隔板装置的传热Nu在二维和三维计算下的结果相同,并且都比无隔板对流装置的传热Nu高许多。这是一个特殊的现象,可给批量计算隔板对流装置热对流的传热特性提供方便,可以直接采用二维计算进行不同隔板几何参数和其他物理参数对传热倍增影响的研究,大大减少计算工作量。通过大量计算发现,在Γ=5的对流装置中加入l=0.12的隔板,当隔板数n≥16时传热通道中会产生单向层流化的流动,可以采用二维计算研究隔板对流装置的传热特性。
2 几何参数对隔板热对流装置传热倍增的影响 隔板几何参数对隔板对流装置传热倍增现象的影响是目前研究的重点问题之一。当隔板数较多时,二维计算可以得到满意的隔板对流装置的传热Nu。当隔板数较少时,传热通道仍为湍流流动,传热Nu的二维计算结果会与三维结果有一些偏差,但由于隔板数较少时湍流流动的传热倍增效果不明显,此处只用于做一些特性规律的对比,不作为讨论重点。
取Ra=108,Pr=5.3,隔板厚度保持l=0.12,对隔板对流装置隔板数n≥16的单向层流化流动展开系列计算。改变隔板顶端的狭缝高度d,研究狭缝高度d对传热Nu的影响。
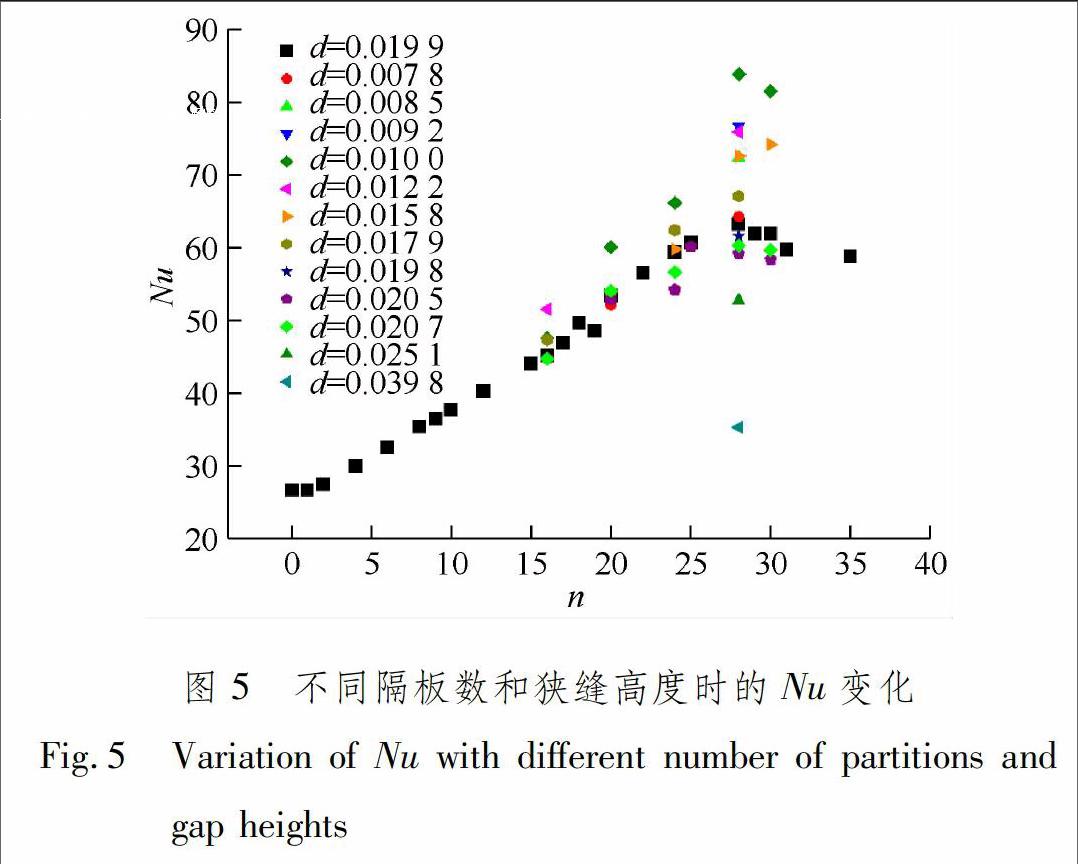
不同隔板数和狭缝高度对Nu的影响见图5。隔板数量较少时,对应d在0.02附近的变化,传热Nu只有一些微小的变化。[16]当隔板数较多时,对应隔板顶端的狭缝高度d的微小变化,计算得到的整体传热Nu发生较大变化。当n=28,d=0.010 0时最大Nu为Numax=83.2,Numax(28)/Nu(0)=3.1,整个装置的传热效率提高210%。与三维计算的无隔板对流装置的Nu=31.4相比,28块隔板d=0.010 0时的Nu是其2.65倍,增加165%,比d=0.02时三维计算的传热增强113%[16]又有增加。传热倍增效果明显进一步提高。
BAO等[16]对加入6块隔板的对流装置进行初步研究,发现系统传热效率最高时对应的狭缝高度d即最优狭缝高度约为d=0.02。与本文结果不同的是,当隔板数n=6时,其系统的流动状态是湍流。当隔板数增加后,传热通道中变为单向层流流动,最优狭缝高度发生变化。从图5中发现,当d=0.010 0时,绿色菱形反映的多隔板数对流装置的传热增强都是最大的,因此可以初步认为,对于隔板厚度相同的单向层流化流动的隔板对流装置,隔板数不同时的最优狭缝高度相近。endprint
隔板对流装置传热Nu随狭缝高度d的变化特性可以说明隔板几何参数对传热特性有显著的影响,需要更多的深入研究,寻找和建立传热倍增特性的有效的变化关系。这项研究对隔板对流装置的传热倍增特性研究和优化设计具有重要的价值。
4 传热通道温度漂移现象与d之间的关系4.1 传热通道温度漂移现象
在隔板对流装置中,热对流由于流动失稳,于狭缝中产生水平流动,改变热边界层附近的温度梯度。狭缝水平流动将温度边界层的热流带入隔板间竖直的传热通道中,使装置的温度分布发生对称破缺,产生传热通道的温度漂移现象。同时,由于温度漂移现象改变浮力分布,形成传热通道中相间的单向层流化的向上热流和向下冷流,从而大大增加传热效率。
在研究初期,隔板对流装置传热通道温度漂移现象中的温度漂移量变化不明显。改变狭缝高度d进一步计算显示,d的变化使传热通道的温度漂移量值有很大的变化。
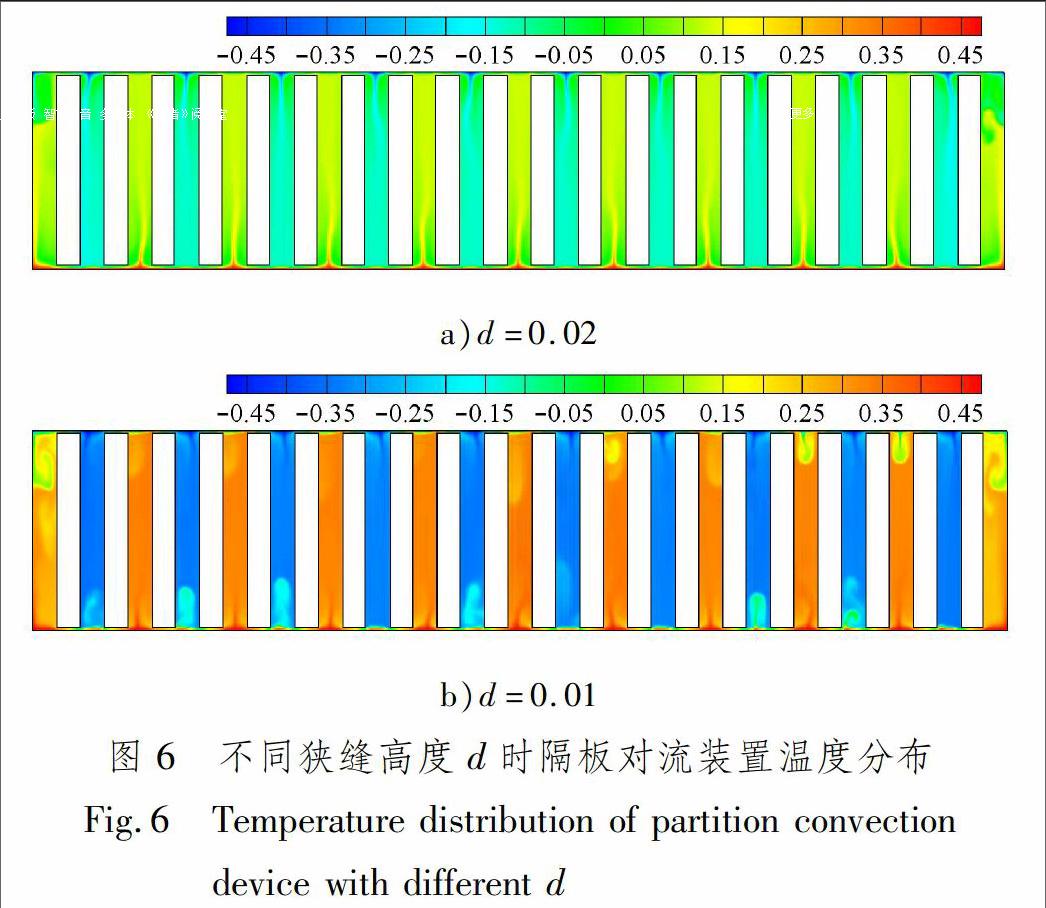
不同狭缝高度时隔板对流装置的温度分布见图6。2个传热通道中的温度漂移量明显不同。d=0.02时的温度漂移量绝对值大约为0.1,d=0.01时的温度漂移量绝对值大约为0.3。d=0.02时的温度漂移量绝对值小于d=0.01时的温度漂移量绝对值。隔板对流装置的温度漂移现象中的温度变化是该装置中明显变化的物理量之一,由此,展开温度漂移变化特性的定量研究。
为定量研究隔板对流装置中的温度漂移现象,定义Td数来表征温度漂移量。每个传热通道Td数的计算过程为先对传热通道的温度沿水平取平均(记为〈θ〉),再沿垂直方向求积分,即
式中:xi为第i个传热通道的横坐标。Td数可以代表每个传热通道中温度分布的平均变化量,即温度漂移量。
狭缝高度d=0.02时的Td数在不同传热通道中的分布情况见图7。隔板对流装置中间部分的传热通道Td数正负相间分布,除两侧的传热通道受侧壁影响外,Td数的大小非常接近。这表明在隔板对流装置的中间部分,每个传热通道的温度漂移量值是相同的。由此可见,隔板对流装置的温度分布具有很好的一致性。因此,可取中间部分传热通道的Td数的绝对值和的平均值计算装置的整体Td数,用于定量描述隔板对流装置的温度漂移现象。
4.2 隔板对流装置的Td数与狭缝高度d的关系
首先对Td数随d的变化特性进行定量研究。对隔板对流装置热对流进行大量的二维DNS模拟:当Ra=108,Pr=5.3,l=0.12时,计算不同隔板数的隔板对流装置的Td数;改变狭缝高度d,得到系列Td数。
隔板数n分别为16,20,24,28和30的隔板对流装置的Td数随d的变化情况见图8,其中标出了Ra=108时温度边界层的厚度δth,可见计算传热倍增现象的狭缝高度d与温度边界层厚度相近。隔板数n≥16时传热通道中的流动为单向层流流动。当d很小时,狭缝中的水平流动无法通过,传热通道几乎不连通,通道中的温度分布不会发生漂移现象,Td数很小。当狭缝高度d略增大后,Td数迅速增大,并很快接近极限值Td,max=0.5(上下底板温度值);而后,随着d继续增大,Td数开始下降。图8中也给出了n=9时Td数随d的变化,可知隔板数较少即湍流流动时Td数随d的变化规律,与隔板数较多在传热通道中形成单向层流流动的变化规律完全不同。图8中不同隔板数的结果反映出Td数随d变化的重要特征,不同隔板数的Td数随d的变化基本重合。也就是说,在隔板对流装置单向层流流动时,Td基本不受隔板数的影响。在给定Γ=5,l=0.12的情况下,加入不同数量的隔板可使得传热通道宽度b发生变化。上述结果表明,传热通道宽度b的变化对Td数的变化影响不大,Td数的变化与狭缝高度d的变化有关。由此分析,狭缝的几何尺寸可能对整个隔板对流装置的流动起到关键的控制作用。
对层流化后隔板对流装置的Td数与d的关系进行曲线拟合。当Γ=5,Ra=108,Pr=5.3,l=0.12,n≥16时,在传热通道中单向层流化流动的条件下,当d≥0.008时,Td数与d满足标度律关系
在隔板对流装置隔板数较多时流动单向层流化后,如何描述Td数与d的标度律关系,其与传热倍增现象之间存在什么样的关系,Td数与其他物理量和几何参数间有什么样的变化规律,有待进一步的深入探讨和研究。
5 结 论
通过DNS数值模拟,研究隔板对流装置的传热倍增特性和传热通道中的温度漂移现象。计算结果显示,在隔板数较多(n≥16)的情况下,传热通道产生单向层流流动,流动具有很好的二维性,隔板对流装置二维和三维DNS模拟的传热Nu计算结果一致。因此,对隔板数较多时传热倍增效果显著的隔板对流装置进行大量的二维数值计算。通过系列的计算结果分析,研究隔板对流装置狭缝高度d的变化对传热倍增和传热通道中温度漂移特性的影响。
研究结果发现,隔板对流装置隔板顶端狭缝高度d的变化对传热Nu影响较大,且不同隔板数的传热Numax都出现在约d=0.01时。二维模拟的隔板对流装置的传热Numax发生在隔板数n=28时,此时Numax=83.2,Numax(28)/Nu(0)=3.1。这表明整个装置的传热效率提高了210%,比文献[16]中d=0.02時传热效率增加130%的结果又增强80%,其传热倍增效果明显地进一步提高。
计算结果显示,狭缝高度d的变化引起传热通道温度漂移量的明显变化。定义传热通道温度漂移量Td数,进行传热通道温度漂移特性的定量研究。通过积分计算传热通道的Td数,结果发现Td数在传热通道中为正负相间分布,除侧壁附近外,装置中间部分的Td数大小基本相同。取中间部分的Td数绝对值和的平均值作为隔板对流装置的温度漂移量Td数,定量研究发现:在隔板数较多、传热通道单向层流流动的情况下,隔板对流装置的Td数与传热通道宽度b基本无关,Td数与狭缝高度d满足标度律关系;隔板数较少、传热通道中仍为湍流流动时,Td数与狭缝高度d不存在标度律关系。endprint
參考文献:
[1] AHLERS G, GROSSMANN S, LOHSE D. Heat transfer and large scale dynamics in turbulent Rayleigh-Bénard convection[J]. Reviews of Modern Physics, 2009, 81(2): 503-537. DOI: 10.1103/RevModPhys.81.503.
[2] XIA K Q. Current trends and future directions in turbulent thermal convection[J]. Theoretical & Applied Mechanics Letters, 2013, 3(5): 1-12. DOI: 10.1063/2.1305201.
[3] DU Y B, TONG P. Enhanced heat transport in turbulent convection over a rough surface[J]. Physical Review Letters, 1998, 81(5): 987-990.
[4] WEI P, CHAN T S, NI R, et al. Heat transport properties of plates with smooth and rough surfaces in turbulent thermal convection[J]. Journal of Fluid Mechanics, 2014, 740(1): 28-46. DOI: 10.1017/jfm.2013.638.
[5] KUNNEN R P J, CLERCX H J H, GEURTS B J. Heat flux intensification by vortical flow localization in rotating convection[J]. Physical Review E: Statistical Nonlinear & Soft Matter Physics, 2006, 74(2): 1-4. DOI: 10.1103/PhysRevE.74.056306.
[6] WEISS S, WEI P, AHLERS G. Influence of the Prandtl number on the heat transport enhancement in rotating turbulent Rayleigh-Bénard convection[C]// Proceedings of 67th Annual Meeting of the APS Division of Fluid Dynamics. American Physical Society, 2014.
[7] KOOIJ G L, BOTCHEV M A, GEURTS B J. Direct numerical simulation of Nusselt number scaling in rotating Rayleigh-Bénard convection[J]. International Journal of Heat and Fluid Flow, 2015, 55: 26-33. DOI: 10.1016/j.ijheatfluidflow.2015.05.016.
[8] LAKKARAJU R, SCHMIDT L E, ORESTA P, et al. Effect of vapor bubbles on velocity fluctuations and dissipation rates in bubbly Rayleigh-Bénard convection[J]. Physical Review E, 2011, 84(3): 247-268. DOI: 10.1103/PhysRevE.84.036312.
[9] GUZMAN N D, XIE Y B, CHENb S, et al. Heat-flux enhancement by vapour-bubble nucleation in Rayleigh-Bénard turbulence[J]. Journal of Fluid Mechanics, 787: 331-366. DOI: 10.1017/jfm.2015.701.
[10] HUANG S D, KACZOROWSKI M, NI R, et al. Confinement-induced heat-transport enhancement in turbulent thermal convection[J]. Physical Review Letters, 2013, 111(10): 104501. DOI: 10.1103/PhysRevLett.111.104501.
[11] CHONG K L, XIA K Q. Exploring the severely confined regime in Rayleigh-Bénard convection[J]. Journal of Fluid Mechanics, 2016, 805: R4. DOI: 10.1017/jfm.2016.578.
[12] XIE Y C, HUANG S D, FUNFSCHILLING D, et al. Effects of polymer additives in the bulk of turbulent thermal convection[J]. Journal of Fluid Mechanics, 2015, 784: R3. DOI: 10.1017/jfm.2015.618.endprint
[13] JOSHI P, RAJAEI H, KUNNEN R P J, et al. Effect of particle injection on heat transfer in rotating Rayleigh-Bénard convection[J]. Physical Review Fluids, 2016, 1(8): 084301. DOI: 10.1103/PhysRevFluids.1.084301.
[14] ZHOU Q, LIU B F, LI C M, et al. Aspect ratio dependence of heat transport by turbulent Rayleigh-Bénard convection in rectangular cells[J]. Journal of Fluid Mechanics, 2012, 710(11): 260-276.
[15] ZHOU Q, LU H, LIU B F, et al. Measurements of heat transport by turbulent Rayleigh-Bénard convection in rectangular cells of widely varying aspect ratios[J]. Science China, 2013, 56(5): 989-994. DOI: 10.1007/s11433-013-5063-z.
[16] BAO Y, CHEN J, LIU B F, et al. Enhanced heat transport in partitioned thermal convection[J]. Journal of Fluid Mechanics, 2015, 784: R5. DOI: 10.1017/jfm.2015.610.
[17] CHORIN A J. Numerical solution of the Navier-Stokes equations[J]. Computational Fluid Mechanics, 1968, 22(104): 745-762.
[18] 徐煒, 包芸. 利用FFT高效求解二维瑞利-贝纳德热对流[J]. 力学学报, 2013, 45(5): 666-671.
XU W, BAO Y. An efficient solution for 2D Rayleigh-Bénard convection using FFT[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013: 666-671.
[19] XI H D, LAM S, XIA K Q. From laminar plumes to organized flows: the onset of large-scale circulation in turbulent thermal convection[J]. Journal of Fluid Mechanics, 2004, 503: 47-56. DOI: 10.1017/S0022112004008079.
[20] GUO Z Y, LI D Y, WANG B X. A novel concept for convective heat transfer enhancement[J]. International Journal of Heat & Mass Transfer, 1998, 41(14): 2221-2225.endprint
