核电站循环水系统进水池结构优化分析

聂小棋, 叶学民, 李达然, 曹祐群, 张莹莹

(1. 华北电力大学 能源动力与机械工程学院， 河北保定 071003;2. 国核电力规划设计研究院， 北京 100095)

核电站循环水系统进水池结构优化分析

聂小棋1,2, 叶学民1, 李达然2, 曹祐群2, 张莹莹1

(1. 华北电力大学 能源动力与机械工程学院， 河北保定 071003;2. 国核电力规划设计研究院， 北京 100095)

通过控制变量的方法，对某核电站进水池拟定的结构参数大小进行适当调整，并通过数值模拟方法得出并推荐了进水池主要结构参数选取范围，从数值模拟的角度证实了该进水池拟定结构参数大小的合理性。

核电站； 进水池; 结构参数; 数值模拟

核电站循环水系统的进水池是泵房前池与循环水泵进口之间的衔接部分，其作用是平稳地过渡前池水流使之均匀扩散，为水泵提供良好的进水流态。循环水泵能否高效运行很大程度上取决于进入其中的水流流态。

当泵房前池的结构尺寸设计不合理时，池内水流容易发生紊乱，进而影响水泵正常运行，严重时还会造成水泵振动甚至停机[1]。范淑琴等[2]通过模型试验发现，不良的进水流态能降低水泵效率4%～16%；邱静等[3]针对水泵机组不规律的振动现象，通过试验对前池水流进行了深入的观察研究，指出池中涡旋是引起机组不规则振动的主要原因；丁天寿[4]通过试验研究，认为前池流态紊乱是水泵效率降低的主要因素；Deeny等[5-6]指出进水池内的漩涡是影响水泵安全运行的主要因素；Akalank等[7]通过实验发现，当池内吸气漩涡含气量达到1%时，会严重影响水泵的运行效率；日本工程协会[8]、美国陆军工程兵团[9]等依据大量的试验给出了进水池重要结构参数的参考范围，但这些设计参数范围有较大的出入，原因可能在实验条件、实验标准及应用的场合有差异。

核电站的循环水量比一般火电机组要大，因此进水池中水流流态相比火电站进水池也会更加复杂。国内对核电站进水池方面的研究比较少，吉红香等[10]通过物理模型实验发现，进水池工况好坏直接影响到水泵的运行效率，指出规划良好进水池结构的必要性；王保田[11]在某核电站一期工程循环水泵进水流道模型试验中发现，通过在水泵吸水口处加装底面椎体能有效阻止水中涡，确保水泵的安全高效运行。

国内外文献对核电站进水池数值模拟方面的研究较少，许多文献通过数值软件对进水池在其他场合的应用进行了模拟并得出相关结论，但这些结论往往由于应用场合以及试验条件的差异，不能完全应用于核电站进水池。因此，笔者采用数值模拟方法对某核电站的进水池进行全三维定常流场计算，探讨该进水池的结构参数及进水流量的不同对池中水流流态造成的影响，着重观察进水流道入口处的流态是否均匀，同时得出最佳的进水池结构参数的参考范围，为实际试验提供依据和参考。

1 核电站循环水系统进水池主要参数

进入水泵的水流一部分从喇叭管前部进入水泵，还有一部分从喇叭管的两侧及后侧进入水泵。理想的进水流场是各个方向进入水泵的水流流量应尽可能相等，因此进水池结构参数的确定要以此为原则。

该核电站进水池为开敞式矩形结构形式，见图1。

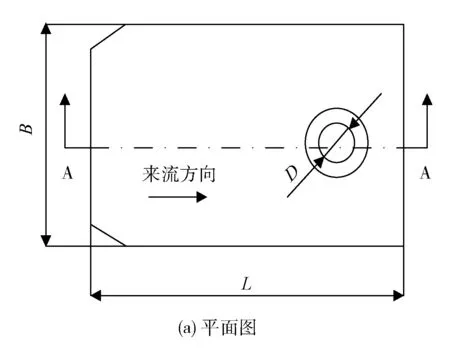
图1 进水池示意图

进水池主要参数为：池长L=5.75D、池宽B=3.62D、悬空高H=0.65D、后壁距E=0.68D及淹没深度h(吸水管直径D=2.8 m，进水池的各个几何参数大小以D作为基准参照表示)。进水池的水泵采用金属混流泵，循环水量Q=20.42 m3/s，水池水深8.7 m。进水池入口处有一小段扩散部分，扩散段长度1.8 m，扩散角29°。进水池入口高3.3 m，宽8 m。数值模拟将以该核电站进水池结构参数为参照，通过控制变量的方法改变进水池几个主要参数，然后进行多次模拟，以期得出最佳水池结构参数的参考范围，同时验证该核电站进水池结构参数的合理性。

2 进水池的数值建模

计算采用标准k-ε模型，壁面函数采用非平衡壁面函数，并应用Simplec算法，离散精度取为二阶迎风格式。模型进口给定为速度进口边界，速度方向垂直于进口界面。由于吸水管长相比管径足够大，可以认定吸水管出口断面处流动是充分发展的，故出口采用自由出流边界条件。进水池表面为自由表面，忽略液面与空气之间的切应力以及热交换，对液面采用刚盖假定，即自由表面设置为对称边界条件。不同区域的交界面上定义interface使绝对流动速度连续，因而实现各个区域交界面上流体能自由贯穿。

网格划分采用分块网格技术，根据该进水池不同部位的结构特点。对边界结构复杂的区域采用适应性强的非结构化网格单独划分网格，部分区域，如吸水管采用cooper方式划分六面体结构网格。吸水管壁面处受到流体的黏性作用，速度梯度较大，为捕捉壁面处的流动特征，在吸水管壁面设置边界层网格。

网格无关性验证时，每个模型网格划分的全局最大尺寸为0.15 m，吸水管边界层第一层网格高度为1 mm，边界层网格层数为20层，每层网格增长因子为1.2。以池长L=5.75D、池宽B=3.5D、悬空高H=0.5D、后壁距E=1D为例，此时模型网格数为291万。另取模型网格全局最大尺寸为0.1 m，边界层网格参数不变，网格数340万，此时精度和前者相差不多，但是计算时间会增加。由于291万的网格可以同时满足计算时间和计算精度的要求，故模型网格全局最大尺寸选取为0.15 m是合适的。基于此在进行模拟时，对进水池结构参数进行变动后，每个模型全局最大尺寸都取为0.15 m，边界层网格参数不变选取如上，能满足网格无关性要求。

3 水力性能优化目标函数

为了定量对进水池参数进行优化设计，建立如下目标函数：

(1) 速度均匀度Vu最大的目标函数。

进水池流态对水泵叶轮的影响主要体现在水泵叶轮前，进水断面处的流速分布，进水流速分布是否均匀会影响到水泵的运行性能。均匀度越高，叶轮前进口断面处的均匀性就越好，水泵运行性能自然也会更佳。

(1)

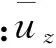
(2) 水力损失hw最小的目标函数。

在考虑进水池最佳结构参数时，水力损失是很重要的参考指标，根据伯努利方程引入水力损失量hw的概念，建立进水池入口断面和吸水管进口断面处的水力损失量目标函数。

hw=E2-E1=

(2)

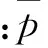
4 数值结果及分析

4.1池宽影响

采用4种不同池宽的方案进行了数值模拟，每个方案中进水池主要参数见表1。

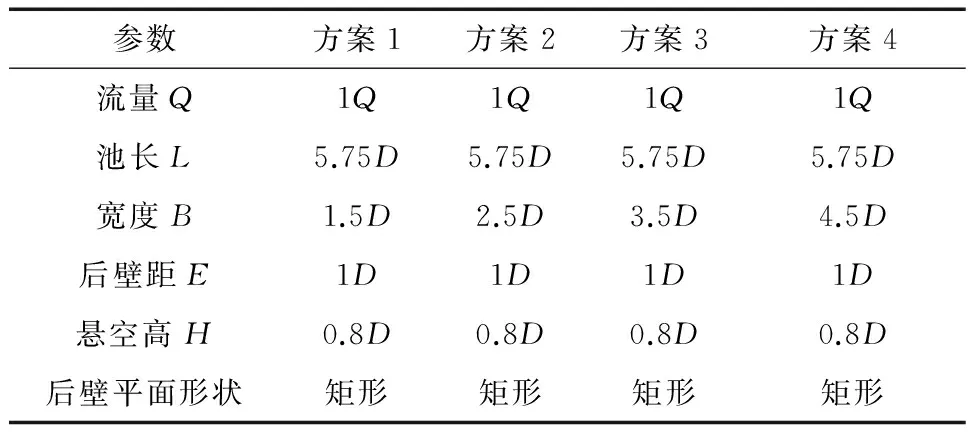
表1 池宽数值模拟方案

图2为池宽对断面均匀度的影响，图3为池宽与水力损失量的关系。

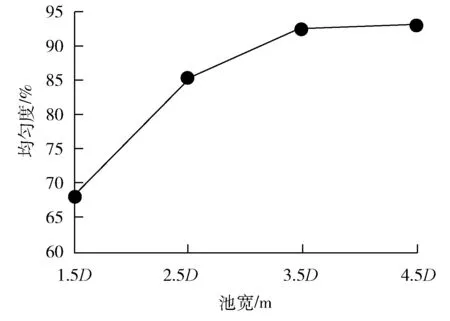
图2 池宽对断面均匀度的影响

图3 池宽与水力损失量的关系

从图2可以看出：当池宽为1.5D时，泵入口断面处均匀度最差；当池宽为4.5D时，断面处均匀度最佳。随着池宽的增加，泵入口断面均匀度不断增加，池宽从1.5D增加到4.5D，断面均匀度提高了37.52%；但随着池宽的不断增加，断面均匀度增加的幅度不断减小，池宽从1.5D增加到2.5D，均匀度增加了23.5%，而池宽从2.5D增加到3.5D时，均匀度增加了8.06%。主要原因是当池宽较小时，池中流速变大，进入水泵的流速分布不均匀，同时过窄的池宽也会使得流向喇叭口的流线曲率增加，容易在喇叭口附近形成漩涡，使得吸水管进口断面流速分布不均匀。当水池宽度变大时，流速降低，同时水池有更大的空间让水流流向水泵时均匀平稳过渡，因此水泵进口断面流速分布更加均匀。不过增大水池宽度的同时，会增加开挖工程量，提高工程成本。当池宽过大时，水池壁面的导向作用也会变差，在池中容易形成偏流和回流，反而可能会恶化进水条件。从图3可以看出：随着池宽的不断增加，水力损失是不断减小的。基于以上分析，推荐进水池池宽选取3D～4.5D。该核电站池宽拟选定为3.62D，在推荐范围内。

4.2池长影响

采用4种不同池长的方案进行了数值模拟，每个方案中进水池主要参数见表2。

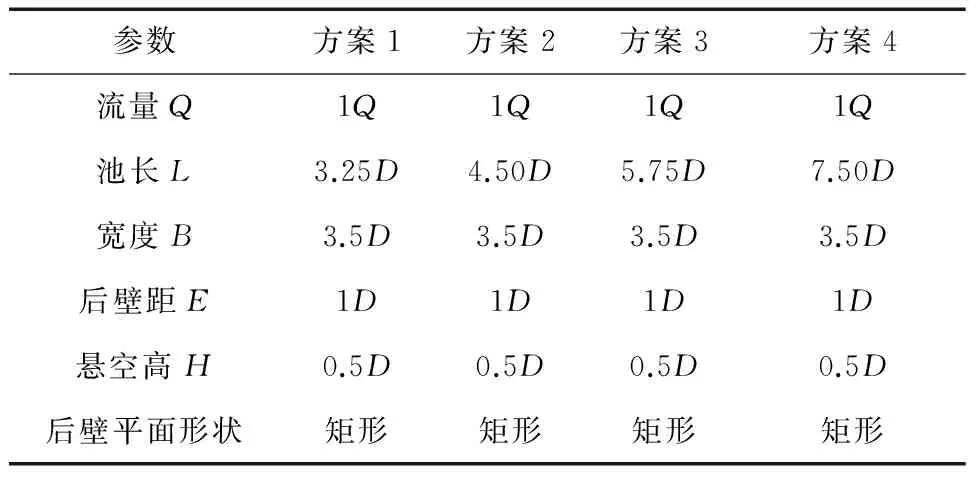
表2 池长数值模拟方案

图4为池长对断面均匀度的影响，图5为池长与水力损失量的关系。

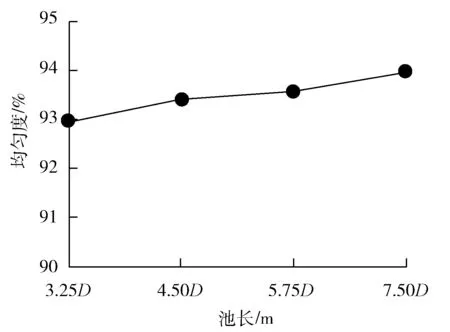
图4 池长对断面均匀度的影响

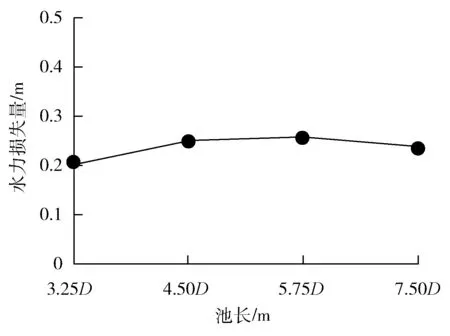
图5 池长与水力损失量的关系

从图4、图5可以看出：当池长大于一定的程度，随着池长的增加，水泵进水口断面均匀度以及水力损失量变化均不明显。因为池长增加到一定的长度后，从进水池进口流入的水流有足够的空间和时间均匀扩散，平稳过渡到水泵进水口处，其断面处均匀度较佳，不再明显变化，水力损失量变化同理。此外增加水池长度，会增加开挖工程量，提高工程成本。基于以上分析，推荐池长为3.5D～6D。该核电站进水池池长拟选定为5.75D，在推荐范围内。

4.3后壁形状影响

采用4种不同后壁形状的方案进行了数值模拟，每个方案中进水池主要参数见表3。

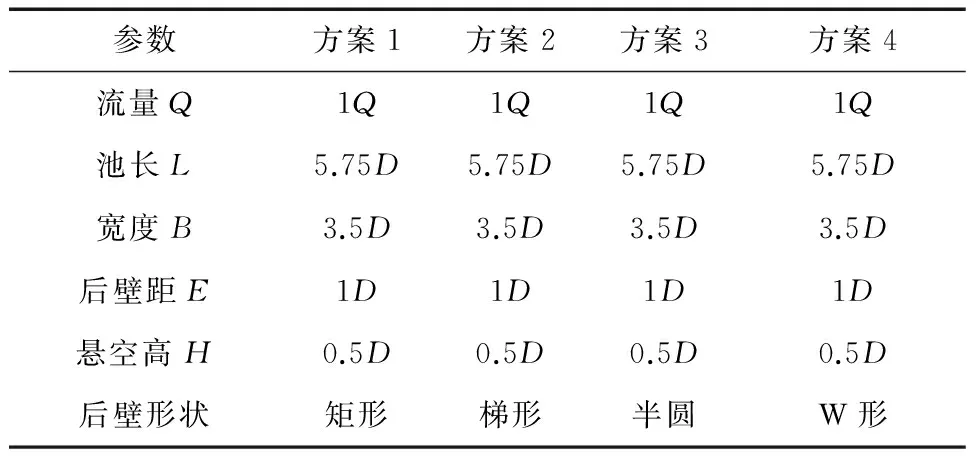
表3 后壁形状数值模拟方案

图6为笔者模拟采用的进水池4种不同形状的后壁。

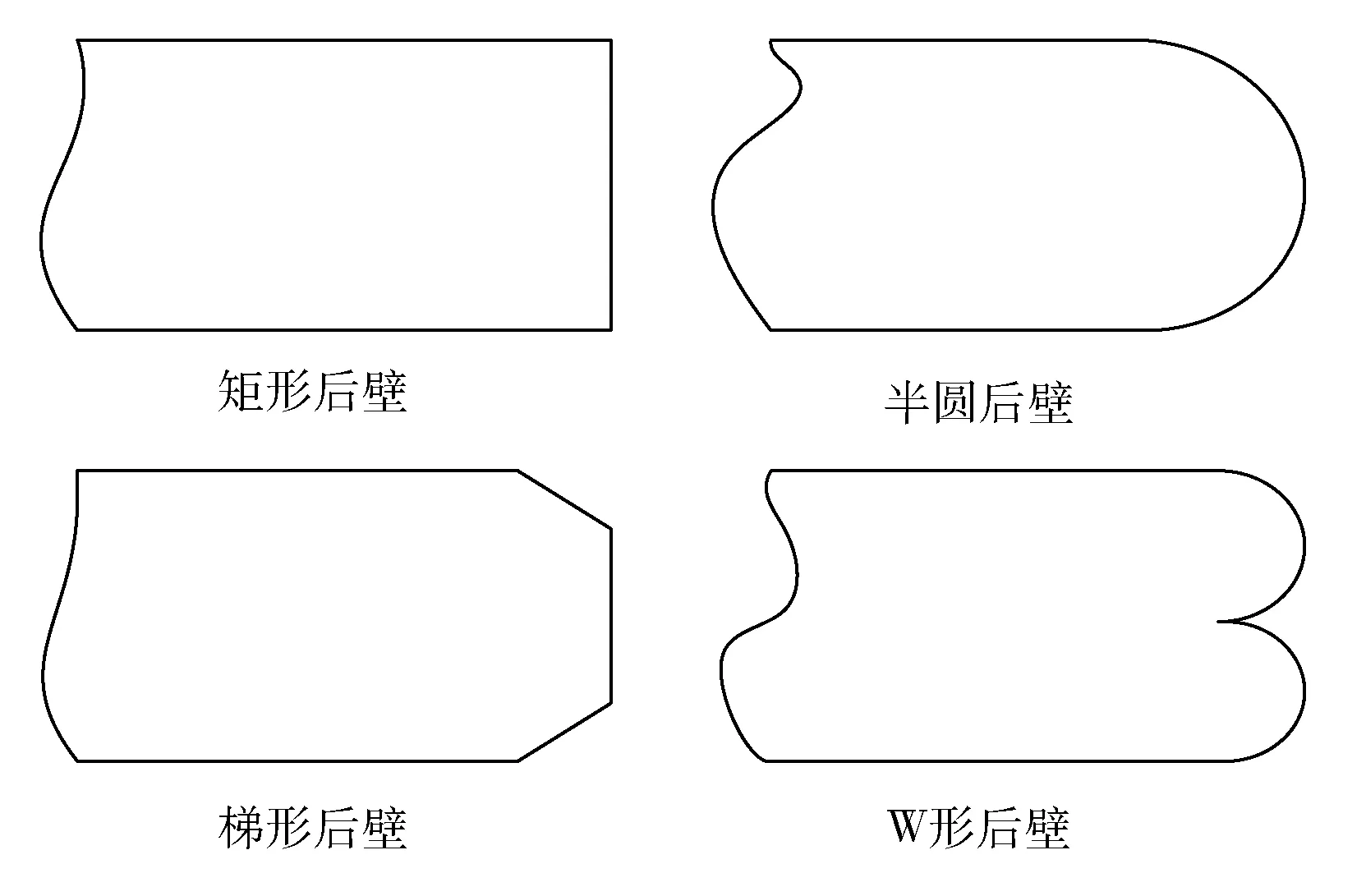
图6 不同形状后壁

表4为后壁形状与均匀度、水力损失量的关系。

表4 后壁形状与均匀度和水力损失量的关系

从表4可以看出：后壁形状从矩形、梯形、半圆到W形，吸水管进口端面的均匀度是不断增加的，进水池采用W形后壁时均匀度相比于矩形后壁提高了1.33%。因为矩形后壁进水池在后壁直角区域为低速区，在该处容易形成回流，使水流流速分布不均匀，不利于水泵进水口处的流态。梯形后壁形状在矩形后壁的基础上进行了结构改良，后壁处的回流区基本消失，对于改善流态起到了较好的效果。半圆后壁形状的进水池同样避免了池中回流的产生，同时池中流体流线和后壁形状也比较一致，因而该后壁有良好的整流效果，进水口断面处均匀度较高。对于W形后壁进水池，后壁中间突出的壁面部分比较接近水泵进水口，能有效改善进入水泵的水流流态，抑制其漩涡和回流的产生，此外该形状后壁和水流流线比较吻合，因此在所罗列的四种后壁形状中，W形后壁具有最佳的整流效果，能使得进水口断面处的均匀度最佳。

从表4可以看出：矩形后壁进水池水力损失量最大，W形后壁进水池水力损失最小，梯形和半圆后壁进水池水力损失量居中。W形后壁相比于矩形后壁水力损失量减少了13.9%。值得指出的是，半圆后壁进水池水力损失量和矩形后壁进水池水力损失量差不多，高于另外两种后壁进水池，原因在于半圆后壁进水池由于结构特点容易在后壁附近形成漩涡，其增加了水力损失量。W形后壁进水池由于其较好的结构特点及整流作用，使得水力损失量最小。

该核电站进水池拟采用的是矩形后壁，基于以上分析，进水池后壁形状建议采用W形后壁。

4.4后壁距影响

采用4种不同后壁距的方案进行了数值模拟，每个方案中进水池主要参数见表5。

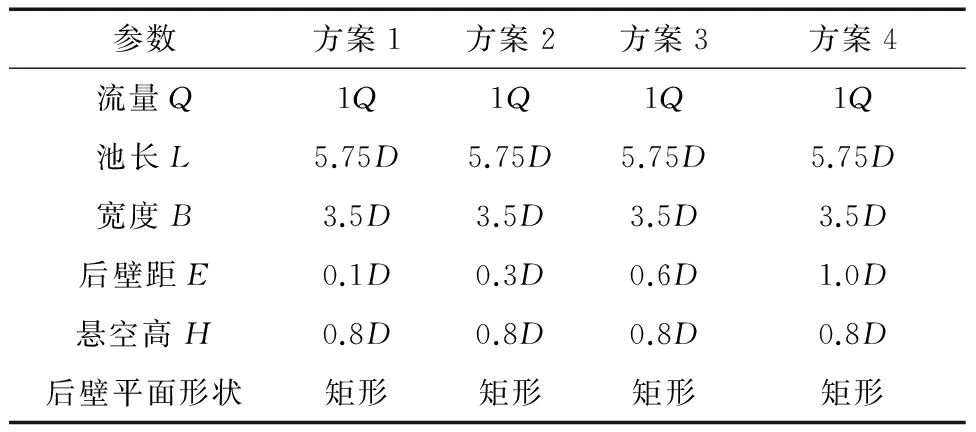
表5 后壁距数值模拟方案

图7为后壁距对断面均匀度的影响，图8为后壁距与水力损失量的关系。

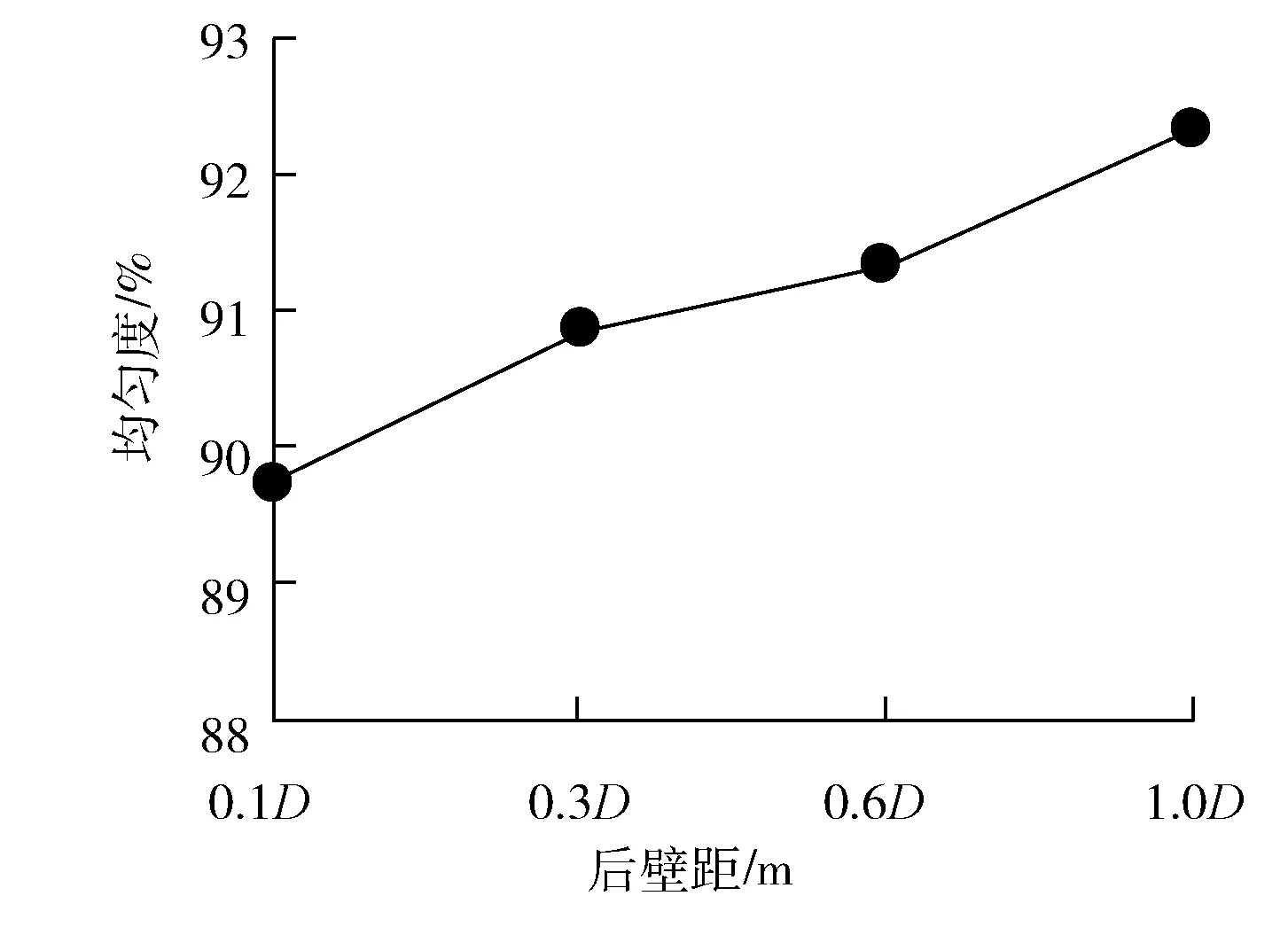
图7 后壁距对断面均匀度的影响

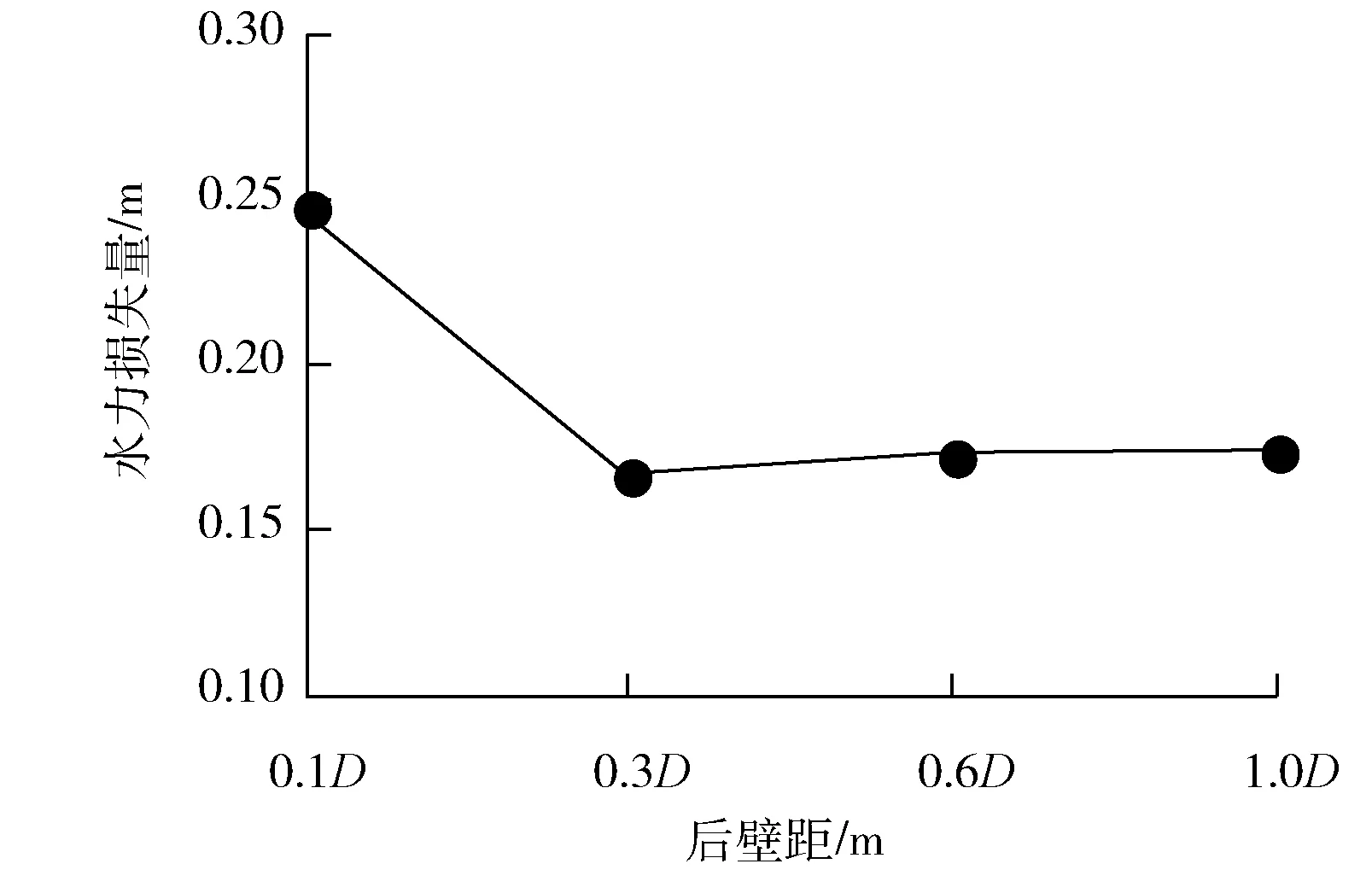
图8 后壁距与水力损失量的关系

从图7、图8可以看出：随着水泵后壁距离增加，均匀度越高，即水泵进水口断面流速分布更加均匀，水力损失量呈逐渐下降趋势。后壁距为1D相比较于后壁距为0.1D时，均匀度提高了2.89%，水力损失量降低了29.02%。原因在于当后壁距离很小时，水流从前面和两侧进入水泵的流量要更多，后侧水流进入得较少，此外水流冲击后壁折返过程中，扩散还未充分均匀就进入了水泵，因此从水泵四周进入吸水管的水流是不均匀的，同样水力损失量也是最大的。当后壁距增加时，水流从四周流入水泵更加趋于均匀，且冲击后壁折返的水流有更大空间平稳过渡到水泵进水口处，因而流速分布更加均匀，水力损失量也越来越小，趋于定值。需要指出的是，当后壁距过大，水流容易产生吸气涡而影响水泵的正常运行。

基于以上分析，推荐进水池后壁距为0.3D～1D。该核电站进水池后壁距拟定为0.68D，在推荐范围内。

4.5悬空高影响

采用4种不同悬空高的方案进行了数值模拟，每个方案中进水池主要参数见表6。

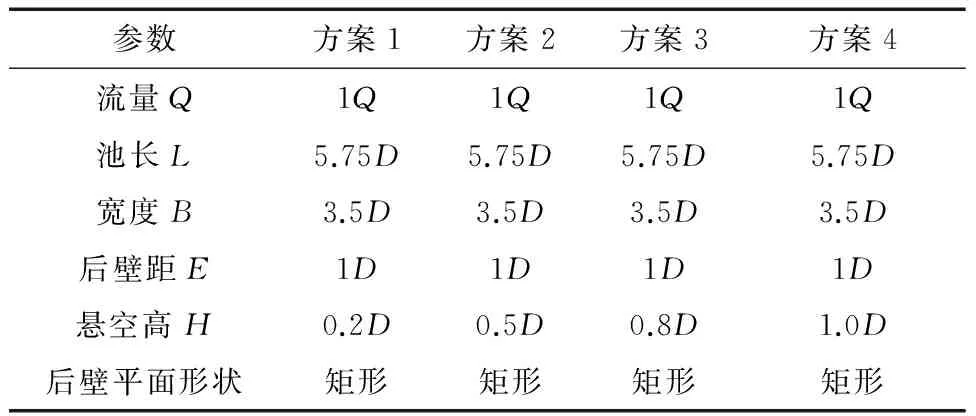
表6悬空高数值模拟方案

图9为悬空高对断面均匀度的影响，图10为悬空高与水力损失量的关系。

图9 悬空高对断面均匀度的影响

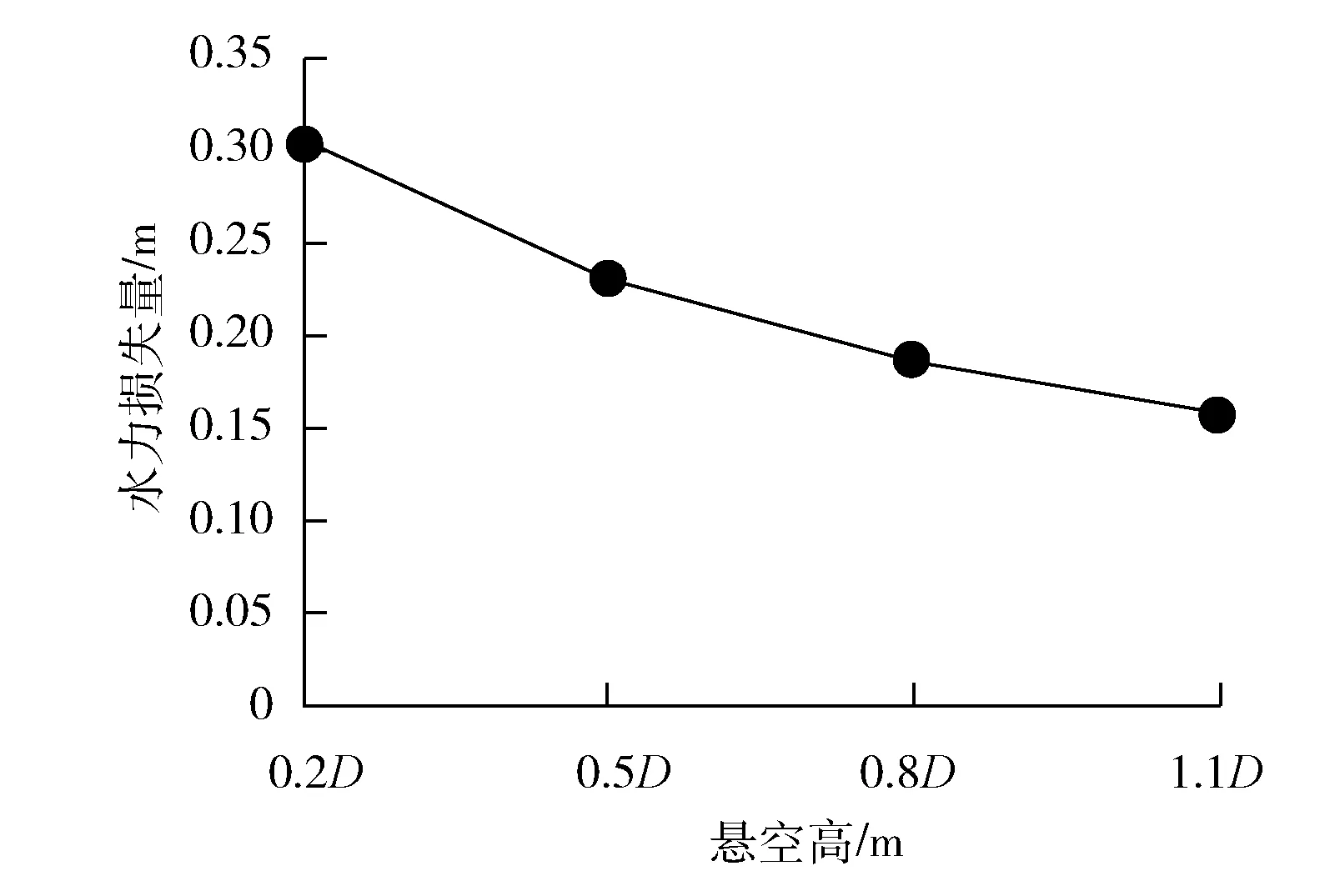
图10 悬空高与水力损失量的关系

悬空高能较大程度上影响进水池中流态，从图9、图10可以看出：随着悬空高的增加，进水口断面水流均匀度变化过程为先增加后减小，流体水力损失量则不断减小，但是减小的幅度在随之降低。悬空高为0.5D时，均匀度最大比悬空高为0.2D时增加13.59%，水力损失减少23.92%。悬空高为1.1D时，水力损失相比于0.8D减小15.69%。悬空高较低时，流向喇叭口的流线曲率增加，速度梯度变化大，容易在喇叭口附近形成漩涡，使得吸水管进口断面流速分布不均匀,水力损失也很大。悬空高过大时，一方面增加了土建工程量，另外容易在液面形成吸气旋涡，使流态变差同时还能影响到水泵的正常运行。

基于以上分析，推荐进水池悬空高为0.5D～1D。该核电站进水池悬空高拟定为0.65D，在推荐范围内。

4.6流量影响

采用4种不同流量的方案进行了数值模拟，每个方案中进水池主要参数见表7。

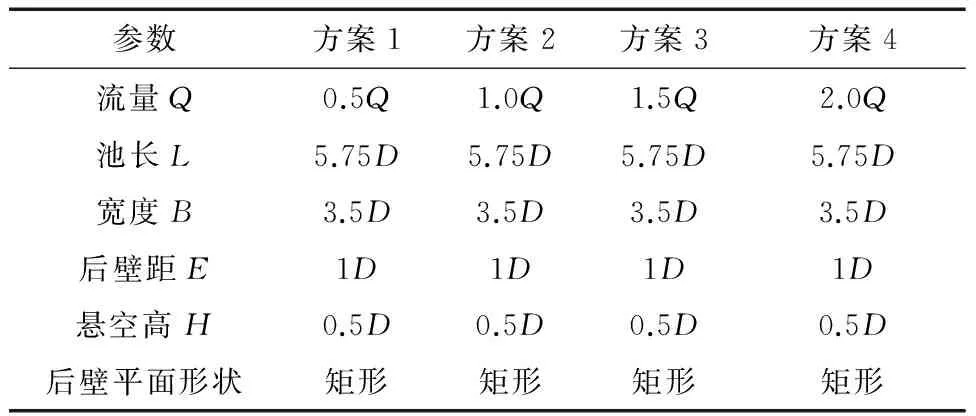
表7 流量数值模拟方案

为了加强对进水池相关参数，引起水流流态变化的认识，现引入流量作为考察的变量。当流量变化时，水泵进水口断面均匀度以及流体水力损失量结果见图11、图12。

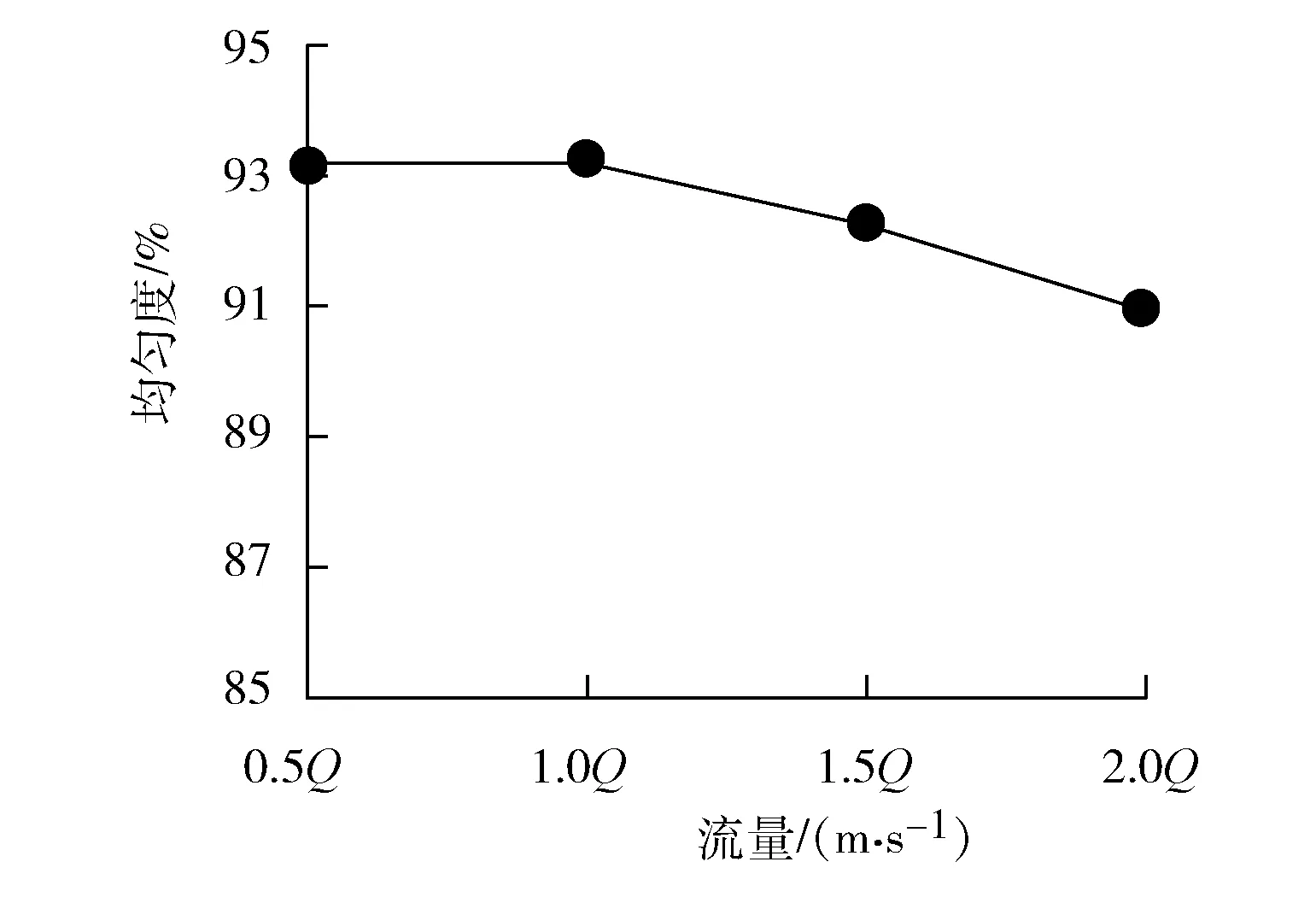
图11 流量对断面均匀度的影响

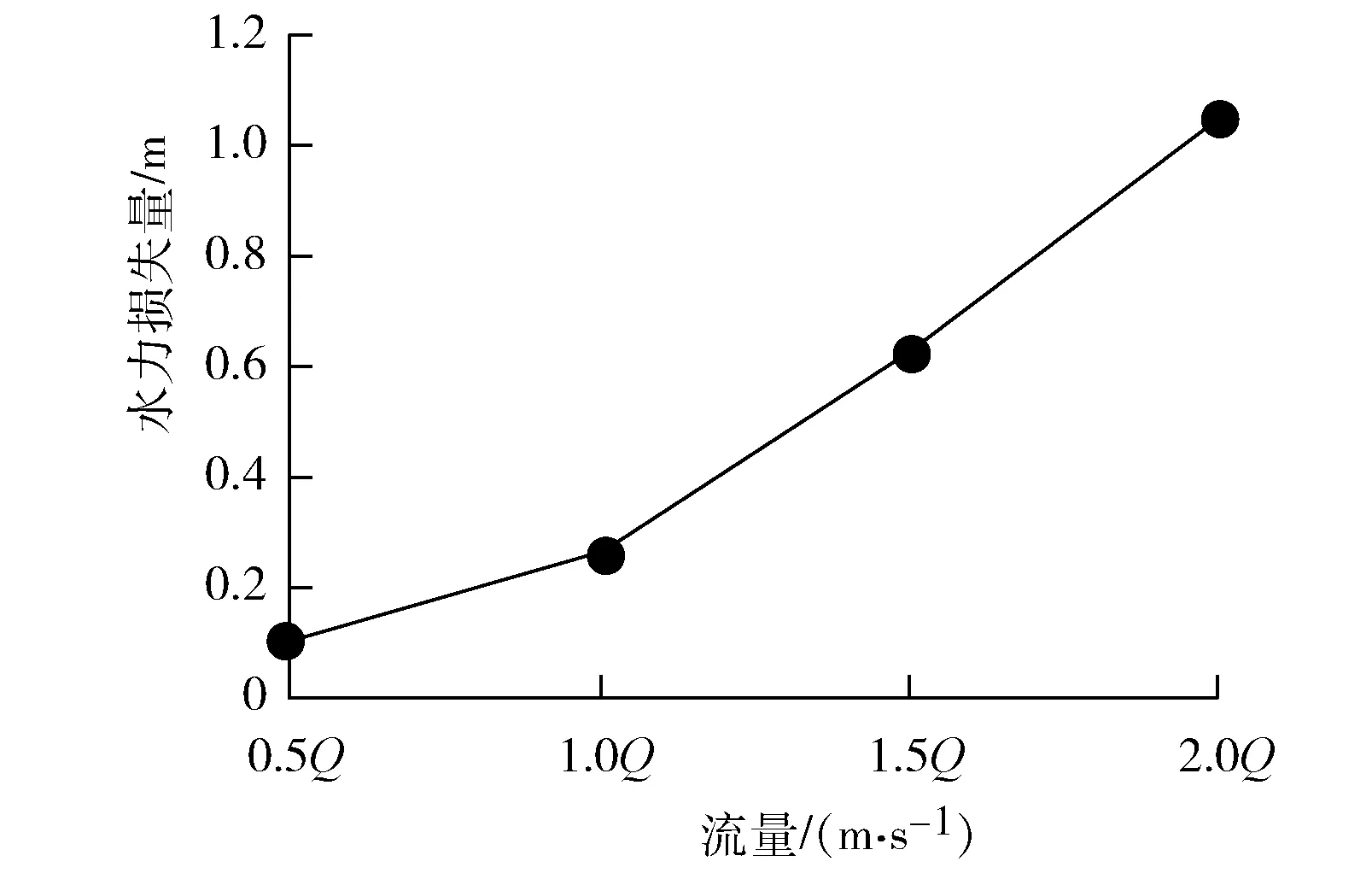
图12 流量与水力损失量的关系

从图11、图12中可以看出：随着流量不断增加，均匀度逐渐减小，水力损失不断增加，且水力损失量和流量近似于二次函数的关系。当进入水池的流量不断增加，水流流速也会随之变大，使得池中的流态趋于复杂，池中更容易出现偏流、回流的不良流态，因此均匀度会下降，而水力损失量会增加。

5 结语

(1) 通过控制变量的方法，对某核电站进水池拟定的结构参数进行适当调整，并通过数值模拟方法得出并推荐了进水池主要结构参数合理的选取范围：池宽3D～4.5D，池长3.5D～6D，后壁距0.3D～1D，悬空高0.5D～1D。

(2) 将某核电站进水池拟定的结构参数和笔者推荐参数范围进行对照，得出如下建议：将进水池后壁形状改为W形，其他参数大小不变。笔者从数值模拟的角度，证实了该进水池结构参数选取的合理性，并提出了改进措施。

(3) 数值模拟结果满足网格无关性要求，所得到的结果可供同类场合参考。

[1] 中华人民共和国水利部. 泵站设计规范[M]. 北京: 中国计划出版社, 1997.

[2] 范淑琴, 仲付维. 抽水站整体模型试验研究[J]. 水利学报, 1987, 18(11): 45-50.

[3] 邱静, 黄东, 黄本胜, 等. 某大型泵站机组振动原因分析及防振临时工程措施[J]. 中国农村水利水电, 2004(12): 103-105.

[4] 丁天寿. 1200LW-60大型泵低效原因浅析及改善措施探讨[J]. 西北水力发电, 2006, 22(5): 89-91.

[5] DENNY D F. An experimental study of air-entraining vortices in pump sumps[J]. Proceedings of the Institution of Mechanical Engineers, 1956, 170(1): 106-125.

[6] REDDY Y R, PICKFORD J A. Vortices at intakes in conventional sumps[J]. Water Power, 1972, 24(3): 108-109.

[7] JAIN A K, RAJU K G R, GARDE R J, et al. Vortex formation at vertical pipe intakes[J]. Journal of the Hydraulics Division, 1978, 104(10): 1429-1445.

[8] Pumping Station Engineering Working Group of Japan Association. Pumping station engineering handbook[M]. Tokyo: Japan Association of Agricultural Engineering Enterprises, 1991.

[9] U. S. Army Corps of Engineers. Hydraulic design guidance for rectangular sumps of small pumping stations with vertical pumps and ponded approaches[R]. Washington D C: U. S. Army Corps of Engineers ,1998.

[10] 吉红香, 邱静, 林美兰, 等. 某核电厂一期工程循环水泵房进水流道物理模型试验研究[J]. 广东水利水电, 2010(10): 20-23.

[11] 王保田. 某核电站一期工程循环水泵进水流道模型试验探讨[J]. 中国电力, 2014, 47(5): 113-117, 135.

StructureOptimizationofaPumpSumpinCirculatingWaterSystemofNuclearPowerPlant

Nie Xiaoqi1,2, Ye Xuemin1, Li Daran2, Cao Youqun2, Zhang Yingying1

(1. School of Energy, Power and Mechanical Engineering, North China Electric Power University,Baoding 071003, Hebei Province, China; 2. State Nuclear Electric Power Planning Design & Research Institute, Beijing 100095, China)

By control variable method, an adjustment of simulated structural parameters was carried out for the pump sump of a nuclear power plant, after which some parameter ranges were recommended for the sump. Above structural parameters of the pump sump were proved to be rational by numerical simulation.

nuclear power plant; pump sump; structural parameter; numerical simulation

2017-03-03；

2017-03-18

聂小棋(1992—)，男，在读硕士研究生，主要从事流体结构优化和流体换热研究。E-mail: 156583707@qq.com

TM623.4; TV 136. 2

A

1671-086X(2017)06-0420-06