Automatic landing system using neural networks and radio-technical subsystems
2017-11-21RomulusLunguMihaiLungu
Romulus Lungu,Mihai Lungu
University of Craiova,Faculty of Electrical Engineering,107 Decebal Blvd.,Craiova,Romania
Automatic landing system using neural networks and radio-technical subsystems
Romulus Lungu,Mihai Lungu*
University of Craiova,Faculty of Electrical Engineering,107 Decebal Blvd.,Craiova,Romania
Adaptive control;Automatic landing;Neural network;PID;Reference model
The paper focuses on the design of a new automatic landing system(ALS)in longitudinal plane;the new ALS controls the aircraft trajectory and longitudinal velocity.Aircraft control is achieved by means of a proportional-integral(PI)controller and the instrumental landing system–the first phase of landing(the glide slope)and a proportional-integral-derivative(PID)controller together with a radio-altimeter–the second phase of landing(the flare);both controllers modify the reference model associated with aircraft pitch angle.The control of the pitch angle and longitudinal velocity is performed by a neural network adaptive control system,based on the dynamic inversion concept,having the following as components:a linear dynamic compensator,a linear observer,reference models,and a Pseudo control hedging(PCH)block.The theoretical results are software implemented and validated by complex numerical simulations;compared with other ALSs having the same radio-technical subsystems but with conventional or fuzzy controllers for the control of aircraft pitch angle and longitudinal velocity,the architecture designed in this paper is characterized by much smaller overshoots and stationary errors.
1.Introduction
Most aircraft have automatic landing systems(ALSs)based on the instrumental landing system1,2and different conventional controllers(proportional-derivative–PD,proportionalintegral – PI,proportional-integral-derivative – PID),1–4for aircraft trajectory’s control during landing,and the use of optimal control laws(H2,H∞,H2/H∞),together with full-or reduced-order observers,provides good results.3,5Because the atmospheric conditions and the dynamics of aircraft are drastically changing during flight and,of course,during landing,it is difficult to land safely by using conventional controllers.To design perfect conventional controllers,one has to know the precise mathematical model of the system to be controlled.Furthermore,the aircraft dynamics may vary with respect to the altitude and the flight conditions.Therefore,the adaptive controllers are better choices.
The presence of unknown or partially known nonlinearities in aircraft dynamics leads to the necessity of using evolved adaptive control architectures in various stages of the flight and especially during landing.Also,the actuators have strongly nonlinear behavior because of the saturation of theirdisplacements and/or mobile elements’velocities.In these cases,in the context of using the inversion of the nonlinearities’dynamics,the adaptive control based on dynamic inversion and neural networks theories is a very good choice.6–9The adapting and the train of the neural networks(NNs)are based on the signals provided by the observers which receive information relative to the error of the automatic control system.The adaptive component of the automatic control law(provided by the NNs)must compensate the inversion(approximation)error of the aircraft dynamics’nonlinear subsystem.For a safety landing,the required information in longitudinal plane is obtained by means of gyro transducers(for aircraft pitch angle–θ and pitch rate–q=˙θ),accelerometers(providing the acceleration signal and,by integration,the aircraft longitudinal velocity),or aerodynamic transducers(for aircraft attack angle10)whether or not the landing control architecture includes an observer.
One of the most commonly employed nonlinear control method is the feedback linearization;in the automatic landing systems’design it is used in some papers,11but the paper presents limited insight into the performance of simulations of this controller and no tests are performed outside of these simulations;the main disadvantage of the feedback linearization method is that all parametric plant uncertainties must appear in the same equation of the state-space representation as the control.
Feed-forward neural networks based on the back propagation learning algorithm have also been used12;the main disadvantage is that the neural networks require a priori training on normal and faulty operating data.Other approaches involves the usage of the time delay neural networks;a controller based on this type of neural networks has been designed,13but its main drawback is related to the flight path track accuracy and the fact that it is enable only under limited conditions.Several neural network control approaches have been proposed based on Lyapunov stability theory.13,14The main advantage of these control schemes is that the adaptive laws were obtained from the Lyapunov synthesis and,therefore,guarantee the system’s stability;the disadvantage is that some conditions should be assumed;these requirements are not easy to be satisfied in practical control application.15Juang designed a new learning technique using a time delay network or networks with backpropagation through time algorithms to control the landing16;the main drawbacks are:(1)the number of hidden units was determined by trial;(2)the convergence time is high.Seven different neural network structures(including critic or Radial Basis Function Neural Networks)have been used for obtaining intelligent auto-landing controllers by means of linearized inverse dynamic model17,18;also,the fuzzy logic technique was used to design controllers that track a pre-determined flight path trajectory for safe landing.19In the research area of optimal synthesis,Ref.20have developed a mixed technique for theH2/H∞control of landing,while Ref.21have used theH∞control technique to design an approach for aircraft automatic and landing.In these papers,the authors did not analyze the robustness of the designed controllers in the presence of sensor errors and external disturbances.22
The auto-landing systems designed in the above mentioned works are characterized by insufficient generality or accuracy;the neural network and dynamic inversion based control approaches could bring improvements.Thus,the paper presents a new adaptive landing architecture for aircraft control in longitudinal plane.According to the authors of this paper,little progress has been reported for the landing flight control systems in longitudinal plane by using neural networks,dynamic inversion concept,linear dynamic compensator,state observer,and PCH block;this motivates the present study.Also,it is interesting to see if the aircraft’s trajectory during landing in longitudinal plane can be tracked with high accuracy by a neural network based controller which uses both the dynamic inversion technique and PCH blocks.The main advantages of the dynamic inversion are:(1)the plant nonlinearities are canceled;(2)the closed loop plant behaves like stable linear system;(3)simplicity in the control structure,ease of implementation,global exponential stability of the tracking error,etc.11On the other hand,the strong point of the neural networks is their approximation ability,these being capable to approximate an unknown system dynamics through learning.A PCH block eliminates the NNs’adapting difficulties.Having in mind the advantages of the NNs,dynamic inversion approach,PCH blocks and the combining of these elements with linear dynamic compensators and state observers,the present paper brings absolute novelty in the search area of ALSs’design.
The paper is organized as follows:the structure of the ALS is given in the second section;the design of the adaptive system for the control of the pitch angle and the longitudinal component of the flight velocity is presented in the third section;in the next section,complex simulations to validate the new designed ALS have been performed and the obtained results are analyzed;finally,some conclusions are shared in the fifth section of the paper.
2.Structure of the new automatic landing system
The automatic control of aircraft during landing(longitudinal plane)is achieved by means of two systems:an automatic system for the trajectory’s control and an automatic system for the control of flight velocity.The automatic system for the control of the flight trajectory in longitudinal plane has two subsystems:(1)the first one is for the aircraft control during the glide slope phase(control of the angular deviation Γ = γ- γc; γ and γcare the real and the calculated slope angles of the aircraft trajectory,respectively),by using an ILS system for the determination of the angle Γ at altitudesH≥H0;(2)the second one is for the aircraft control during the flare phase by means of a radio-altimeter(control of the altitudeH,H<H0,H0– the altitude at which the glide slope phase ends and the second landing phase begins).There are many papers in the literature which threat the control of aircraft in lateral-directional plane in the presence of crosswind.These systems cancel the angular deviation of aircraft with respect to the runway direction,the deviation of the flight direction relative to the runway,and aircraft lateral velocity.Concluding,the control of aircraft in the lateral-directional plane(one landing phase:initial approach)can be achieved by means of other automatic control systems,while the control in longitudinal plane(two landing phases:glide slope and flare)can be achieved by using the neural networks based adaptive system presented in this paper.
The controllers for the glide slope and flare act toward changing the calculated pitch angle θc;the pitch angle θ may be controlled,for example,by using a PD controller.This contains controllers for the glide slope,flare,pitch angle,and flight velocity11;there,the wind shears and the errors of the sensors have been taken into consideration.
To compensate the influence of the unknown or partially known nonlinearities from the dynamics of aircraft and actuators,the PD controllers for aircraft pitch angle and longitudinal velocity should be replaced with adaptive architectures based on dynamic inversion and neural networks.The structure of the new automatic system for aircraft control in longitudinal plane is given in Fig.1;U0is the velocity from the moment when aircraft begins the descent along the glide slope,R–the distance between aircraft and the runway threshold,τ–the time constant associated to the flare curve,α–the attack angle,U– aircraft longitudinal velocity,y=[θ,U]T– the controlled output vector,yc=[θc,Uc]T– the calculated output vector,X–horizontal distance covered during landing,x=[Vx,α,ωy,θ,H]T– the state vector of the longitudinal dynamics, δeand δT– the states associated to the actuators(δe– the elevator deflection and δT– the throttle command),u=[δe,δT]T–the command vector,δecand δTcare the commands applied to elevator and to engines,respectively;the significance of the other variables in Fig.1 are to be presented later in this paper.The actuators are described by the equation:
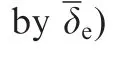
TeandTTare the time constants associated to the elevator and engine,respectively.The linearized dynamics of aircraft longitudinal motion(with respect to the landing trajectory)is4:
Above,V0is the nominal value of aircraft speed.
The linearization of an aircraft’s nonlinear dynamics is generally based on the small disturbances’method with respect to an equilibrium trajectory.Here,the linear model of the aircraft during landing consists of Eqs.(1)–(3).
3.Design of the new automatic landing system
The obtaining of the aircraft desired landing trajectory mainly involves two variables’control:the forward speed(Vx)and the pitch angle(θ).According to the landing requirements,all types of aircraft must firstly descend from the cruising altitude to a lower one;meanwhile,the aircraft speed is also reduced from the cruising value to an approach value and,after that,it remains constant.So,when we choose the desired trajectory,we firstly choose the desired forward speed.
The structure of the adaptive system for the control of the output vector y=[θ,U]T– is presented in Fig.3(Fig.3(a) –complete form,(b)–simplified form),where the block A(having the input u and the output y)represents the longitudinal dynamics of aircraft together with the actuators.This system may be described by the general equations:
with x=[U,α,q,θ,H,δe,δT]T,u=[δec,δTc]T,and y=[θ,U]T;fandhare nonlinear functions,generally unknown or linear functions obtain in the linearization process with respect to the landing trajectory in longitudinal plane;in this paper,we assume thath(x)is a uniquely invertible function.The aircraft linear dynamics in longitudinal plane is obtained(deduced)from the aircraft nonlinear dynamics by linearization and by using the exact total differential method.4The linearization has been made around a speci fic operating point(regime)–flight at constant altitude,the initial angular rates(roll,pitch,and yaw angular rates)being null.
Let us considerri–the relative degrees of the system described by Eq. (4) with respect to the variablesyi,i=1,2;y=[y1,y2]T=[θ,U]T.The system described by Eq.(4)may be described by means of the equations:
one has separated the derivatives that do not depend onufrom the componentshridepending on u.The vectors λiand Yihave the following forms:
The system described by Eq.(5)is modeled by the block diagram in Fig.4,where
The system described by Eq.(5)may be put under the vectorial form:
with
otherwise,we have:
ε=[ε1,ε2]Tis the approximation(inversion)error of the function hr,which acts as a disturbance that must be compensated by an adaptive component of the control law.

This component is calculated with respect to the signals provided by the reference model(command filter).
The control law^v may be chosen of the following form6:

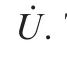
with the notations
Thus,the relative degrees are:r1=3 andr2=2,r=5.Therefore,the transfer functionsHdi(s)have the forms:
Putting together the two Eq.(17),one gets:
From Eqs.(21)and(22),by identification,it results^v and ε.Thus,according to Eq.(10),
Now,replacing Eq.(25)in Eq.(14),one obtains the equation:
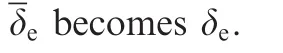
The main purpose of the Pseudo Control Hedging block is to prevent the adaptive element of a control system from trying to adapt to a class of system input characteristics(characteristics of the plant or of the controller).To achieve this issue,the control law is prevented from ‘seeing”the system characteristic;preventing the adaptive element from ‘knowing” about a system’s characteristics means to prevent that adaptive element from seeing the system characteristic as model tracking error.On the other hand,the adaptive controllers are sensitive to actuator nonlinearity.That is why,in these controllers’architecture,one may introduce a block which limits the pseudocontrol by means of a component representing an estimation of the execution element’s dynamics.In this paper,we introduce a PCH block which limits the signalvwith a component representing the actuator dynamics’estimation.Thus,PCH‘moves back” the reference model,introducing correction responses of the reference models with respect to the estimation of the execution element’s position.The signal provided by PCH(vh1)is a reference model’s additional input.23
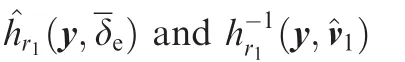
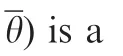

modeled by the block diagram in Fig.5(b).
The states Yi,i=1,2 having the form in Eq.(6)i.e.the vectors associated to the reduced-order subsystem having the inputviand the outputyi,with the transfer functionHdi(s)verify the equation:

From the state Eq.(32),the vectorial state equation(the equation of the reduced-order subsystem in Fig.3(b),having the input v,the output y,and the transfer function Hd(s))is obtained;it is:
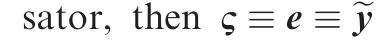
The two components of the output and of the output vector of the linear dynamic compensator are expressed as:
Replacing Eq.(42)in Eq.(40),one obtains the state equation:
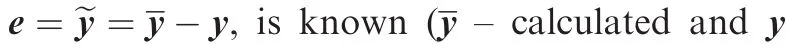
and which is modeled by the state equation5:
where L is the gain matrix of the observer;Eq.(46)is equivalent with the following one:
The gain L is calculated such that the matrix~A is asymptotically stable.
The adaptive control law is calculated by using the formula7:
where W and V–the weights of a neural network(NNc)are the solutions of the equations’system24:

withn1– the number of neurons in the neural network’s input layer,d– the sample step,whileIi,i=1,n1are the outputs of the neural network.We considered that NNcis a feed-forward type neural network having 3 layers:an input layer(withn1neurons),a hidden layer(withn2neurons),and an output layer(withn3neurons);the weights of the neural network have the forms5:
vi,jare the weights associated to the connections between the input layer and the hidden layer,whilewj,kare the weights associated to the connections between the hidden and the output layer.The relationship between the functions σj(for the hidden layer)and the outputs of the NNc(vak,k=1,n3)are25:
bvandbware the biases of the neural network.The sigmoid function σ(z)= σ(VTη)has the form:
ajbeing the activation potentials whose values are different for each neurons;
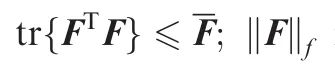
Now,we make a brief stability analysis of the system in Fig.1:

(2)The stability of the two outer loops(one for the first landing phase and one for the second one):imposing negative roots for the afferent characteristic equations,one obtains the coef ficients of the two controllers.
Concluding,the synthesis(the design)of the system in Fig.1 involves the calculation of the controllers’coefficients in conditions of stability.
4.Numerical simulation results
To study the functionality of the new designed ALS,we consider a light aircraft(Charlie type)having the matrices from Eq.(3)of the following forms2:

To calculate the parameters of the two controllers(glide slope and flare),we impose negative roots for the linear subsystems which have on feedback ways the ILS system and the radio-altimeter,respectively;these two subsystems have,on their direct ways,the glide slope/flare controllers in series with the linear automatic subsystem for the adaptive control of the pitch angle;this adaptive subsystem (closed by unitary negativefeedbacks)hason itsdirectwaystheblocks(kp1+kd1s) andHd1(s)=1/s2(s+1). The following values resulted:kc=0.2°/V,T1=0.4s,T2=0.04s,Tc=30s,k′c=-1.5(°)/(m ·s-1),Ti=7.5 × 103s,Td=0.9 s.
The new architecture of ALS(Fig.1)is software implemented in Matlab/Simulink environment and we obtained the time characteristics for the glide slope landing phase(Fig.6)and flare landing phase(Fig.7);in Fig.8,the characteristicsH(X)is plotted;Xrepresents the horizontal distance covered by aircraft during landing.If the actuator associated to the elevator deflection is nonlinear,its models is the one presented in Fig.2;in this case,it is good to use a PCH block(vh1≠0)because it allows the system to work in the linear zones of the nonlinearities.As we already stated above,the signal provided by the PCH block is a reference model’s additional input.Thus,in Figs.6–8,we analyze the influence of Pseudo Control Hedging usage on the variables describing the new designed ALS,taking or not into account the signal from the PCH block.All the characteristics prove the new ALS’s stability and its small overshoots;on the other hand,the differences between the two cases(with and without PCH block)are visible.The usage of a PCH block(when the actuator is nonlinear)does not modify the final values of the variables,but it decrease the transient regime period.The landing begins at a longitudinal speed initially exceeding the nominal speed by 3 m/s(first mini-graphic in Fig.6).The speed should be reduced to the normal speed(67 m/s)and then kept at this value;the landing process begins at 100 m(seventh mini-graphic in Figs.6 and 8),while the flare phase begins at 3.25 m(seventh mini-graphic in Figs.7 and 8).From Figs.6 and 7,we can see that the final error between the desired path and the actual path(altitude error)is less than 0.5 m during the glide slope phase and 0 m for the flare.These errors are very good if the Federal Aviation Administration(FAA)accuracy requirements for Category III(the best category)are analyzed28;according to FAA Category III accuracy requirements,the vertical error(altitude deviation with respect to its nominal value)must be less than 0.5 m(first landing phase)and 0 m(second landing phase).From the forward speed’s point of view,the error is less than 0.3 m/s(first mini-graphics in Figs.6 and 7);also,the aircraft slope angle tends to its desired value: γ→ γc=-2.5°,for the first landing phase,and γ→ γc=0°for the second phase.
The problem of landing has been discussed in other papers,different types of ALSs being designed.For the same aircraft type,we can make a brief comparison between the obtained characteristics with the ones in other paper1;this ALS consists of:an ILS system,a radio-altimeter,and two conventional controllers(a proportional-derivative controller for the pitch angle and a proportional controller for the flight velocity).We can remark that in the case of the ALS designed in the present paper,the dynamic regimes are slightly slower than the onesforconventionalcontrollersand similarto fuzzy controllers,but the overshoots and stationary errors are much better,this leading to the conclusion that the neural networksbased adaptive controllers are more efficient than the conventional and fuzzy ones for aircraft landing(see Table 1).Our new ALS uses modern design technique based on the usage of a feed-forward neural network and of the dynamic inversion concept,this bringing advantage over classical and fuzzy control techniques:our new adaptive control method has applicability to problems involving multivariate systems with cross-coupling between channels;moreover,by using PCH blocks,the non-linear constraints are generally well-handled.

Table 1 Comparison between overshoot of the neural networks-based adaptive controllers,conventional and fuzzy ones.
5.Conclusions
The ALS designed in this paper controls the landing trajectory and the longitudinal velocity by means of two controllers(a glide slope controller and a flare one-P.and PID forms,respectively)and an adaptive control system with neural network,based on the dynamic inversion concept,having as components:a linear dynamic compensator(PD type),a linear observer,two reference models,and a PCH block for the delay of the signal provided by the pitch angle’s reference model(to eliminate the neural network adapting difficulties which appear because of the actuators’nonlinearities).In the design process of the adaptive control system,we have split the aircraft longitudinal dynamics into two vectorial components:Hd(s)(the matrix consisting of the transfer functions of the linear reduced-order subsystems associated to aircraft pitch angle and longitudinal velocity)and hr(y,u).This decomposition is based on the two differential equations associated to aircraft dynamics;these equations express the relative degrees with respect to the main two variables(aircraft pitch angle and its longitudinal velocity)and provide the vectorial functions hr(x,u)and ε– the inversion error(error of the hrfunction’s approximation).Then,we chose the reference model and we designed the control law,the PCH block,the linear dynamic compensator,the linear observer,and the neural network.The aircraft dynamic characteristics(obtained in Matlab/Simulink through numerical simulation for the new ALS–Fig.1)are characterized by much smaller overshoots and stationary errors than the ones associated to the ALSs based on conventional controllers or fuzzy controllers.
Acknowledgements
This work was supported by the Grant No.89/1.10.2015(Modern architectures for the control of aircraft landing)of the Romanian National Authority for Scientific Research and Innovation,CNCS–UEFISCDI,project code PN-IIRU-TE-2014-4-0849.
1.Lungu R,Lungu M,Grigorie TL.ALSs with conventional and fuzzy controllers considering wind shears and gyro errors.J Aerospace Eng2000;26(4):794–813.
2.McLean D.Automatic flight control systems.New York:Prentice Hall Publisher;1990.
3.Lungu R,Lungu M,Grigorie TL.Automatic control of aircraft in longitudinal plane during landing.IEEE Trans Aerospace Electron Syst2013;49(2):1338–50.
4.Lungu M.Sisteme de conducere a zborului.Craiova:Sitech Publisher;2008.
5.Lungu M,Lungu R.Estimarea sta˘rii aparatelor de zbor(State estimation of the flying objects).Craiova:Sitech Publisher;2014.
6.Calise AJ,Hovakymyan N,Idan M.Adaptive output feedback control of nonlinear systems using neural networks.Automatica2001;37(8):1201–11.
7.Calise AJ,Lee S,Sharma M.Direct adaptive reconfigurable control of a tailless fighter aircraft.AIAA guidance,navigation,and control conference and exhibit.Reston:AIAA;1998.
8.Calise AJ,Lee H,Kim N.High bandwidth adaptive flight control.AIAA guidance,navigation and control conference;2000 August 14–17;Montreal,Canada.Reston:AIAA;2000.
9.Singh S,Padhi R.Landing of unmanned aerial vehicles using dynamic inversion.Proceedings of international conference on aerospace science and technology;2008 June 26–28;Bangalore,India;2008.
10.Aron I,Lungu R,Cismaru C.Sisteme de navigatie aerospatiala.Craiova:Scrisul Romanesc Publisher;1989.
11.Singh S,Padhi R.Automatic path planning and control design for autonomous landing of UAVs using dynamic inversion.American control conference riverfront.2009 June 10-12;St.Louis,U.S.A.Piscataway(NJ):IEEE Press;2009.
12.Wagner T,Valasek J.Digital autoland control laws using quantitative feedback theory and direct digital design.J Guid,Control,Dyn2007;30(5):1399–413.
13.Jang JO,Jeon GJ.A parallel neuro-controller for DC motors containing nonlinear friction.Neurocomputing2000;30(1):233–48.
14.Seshagiri S,Khalil HK.Output feedback control of nonlinear systems using RBF neural network.IEEE Trans Neural Networks2000;11(1):69–79.
15.Wai RJ.Development of new training algorithms for neurowavelet systems on the robust control of induction servo motor drive.IEEE Trans Ind Electron2002;49(6):1323–41.
16.Juang JG,Cheng KC.Application of neural networks to disturbances encountered landing control.IEEE Trans Intell Transp Syst2006;7(4):582–8.
17.Saini G,Balakrishnan SN.Adaptive critic based neuro-controller for autolanding of aircraft.Proceedings of the American control conference;1997 June 6–6;New Mexico,USA,Piscataway(NJ):IEEE Press;1997.
18.Juang JG,Chang HH,Cheng KC.Intelligent landing control using linearized inverse aircraft model.Proceedings of American control conference;2002.p.3269–74.
19.Raj KD,Tattikota G.Design of fuzzy logic controller for auto landing applications.Int J Sci Res Publ2013;3(5):1–9.
20.Kumar V,Rana KP,Gupt V.Real-time performance evaluation of a fuzzy PI+fuzzy PD controller for liquid-level process.Int J Intell Control Syst2008;13(2):89–96.
21.Lau K,Lopez R,Onate E.Neural networks for optimal control of aircraft landing systems.Proceedings of the world congress on engineering;2007 July 2–4;London,U.K.;2007.p.1–8.
22.Lungu R,Lungu M.Automatic control of aircraft in lateraldirectional plane during landing.Asian J Control2016;18(3):1–16.
23.Johnson EN,Calise AJ.Pseudo-control hedging:a new method for adaptive control.Advances in navigation guidance and control technology workshop;2000 November 1–2;Redstone Arsenal,Alabama,U.S.A.;2000.
24.Chwa D,Choi J.Adaptive nonlinear guidance law considering control loop dynamics.IEEE Trans Aerospace Electron Syst2003;39(4):1134–43.
25.Johnson EN,Calise AJ,Rysdyk R,Shirbiny EA.Feedback linearization with neural network augmentation applied to X-33 attitude control.AIAA guidance,navigation and control conference and exhibit;2000 August 14–17;Dever,U.S.A.Reston:AIAA;2000.p.1–11.
26.Calise A,Johnson EN,Johnson MD,Corban JE.Applications of adaptive neural–networks control to unmanned aerial vehicles.J Harbin Inst Technol2006;38(11):1865–9.
27.Mori R,Suzuki S.Neural network modelling of lateral pilot landing control.J Aircraft2009;46(5):1721–6.
28.Braff R,Powell JD,Dorfler J.Applications of GPS to air traffic control.Global positioning system:theory and applications,Reston,vol.II.Progress in astronautics and aeronautics.Reston:AIAA;1996.p.327–74.
16 February 2016;revised 29 April 2016;accepted 27 May 2016
Available online 7 January 2017
Ⓒ2017 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.This is anopenaccessarticleundertheCCBY-NC-NDlicense(http://creativecommons.org/licenses/by-nc-nd/4.0/).
*Corresponding author.
E-mail address:Lma1312@yahoo.com(M.Lungu).
Peer review under responsibility of Editorial Committee of CJA.
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Anti-plane problem of four edge cracks emanating from a square hole in piezoelectric solids
- Stress analysis and damage evolution in individual plies of notched composite laminates subjected to in-plane loads
- Drilling load modeling and validation based on the filling rate of auger flute in planetary sampling
- An adaptive attitude algorithm based on a current statistical model for maneuvering acceleration
- Spacecraft attitude maneuver control using two parallel mounted 3-DOF spherical actuators
- Angular velocity determination of spinning solar sails using only a sun sensor
