A multi-objective multi-memetic algorithm for network-wide conflict-free 4D flight trajectories planning
2017-11-20SuYANKaiquanCAI
Su YAN,Kaiquan CAI
School of Electronics and Information Engineering,Beihang University,Beijing 100191,China Beijing Key Laboratory of Network Enabled Collaborative ATM,Beijing 100191,China
A multi-objective multi-memetic algorithm for network-wide conflict-free 4D flight trajectories planning
Su YAN,Kaiquan CAI*
School of Electronics and Information Engineering,Beihang University,Beijing 100191,China Beijing Key Laboratory of Network Enabled Collaborative ATM,Beijing 100191,China
Available online 20 April 2017
*Corresponding author at:School of Electronics and Information Engineering,Beihang University,Beijing 100191,China.
E-mail address:caikq@buaa.edu.cn(K.CAI).
Peer review under responsibility of Editorial Committee of CJA.
Production and hosting by Elsevier
http://dx.doi.org/10.1016/j.cja.2017.03.008
1000-9361©2017 Production and hosting by Elsevier Ltd.on behalf of Chinese Society of Aeronautics and Astronautics.
This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
Under the demand of strategic air traffic flow management and the concept of trajectory based operations(TBO),the network-wide 4D flight trajectories planning(N4DFTP)problem has been investigated with the purpose of safely and efficiently allocating 4D trajectories(4DTs)(3D position and time)for all the flights in the whole airway network.Considering that the introduction of large-scale 4DTs inevitably increases the problem complexity,an efficient model for strategiclevel conflict management is developed in this paper.Specif i cally,a bi-objective N4DFTP problem that aims to minimize both potential conflicts and the trajectory cost is formulated.In consideration of the large-scale,high-complexity,and multi-objective characteristics of the N4DFTP problem,a multi-objective multi-memetic algorithm(MOMMA)that incorporates an evolutionary global search framework together with three problem-specific local search operators is implemented.It is capable of rapidly and effectively allocating 4DTs via rerouting,target time controlling,and flight level changing.Additionally,to balance the ability of exploitation and exploration of the algorithm,a special hybridization scheme is adopted for the integration of local and global search.Empirical studies using real air traffic data in China with different network complexities show that the proposed MOMMA is effective to solve the N4DFTP problem.The solutions achieved are competitive for elaborate decision support under a TBO environment.
©2017 Production and hosting by Elsevier Ltd.on behalf of Chinese Society of Aeronautics and Astronautics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
Air traffic flow management;
4D trajectory planning;
Multi-memetic algorithm;
Multi-objective optimization;
Network-wide strategic con
f
l ict management
1.Introduction
In recent decades,the ever-growing air traffic demands lead to a high level of saturation in the airspace,which results in increasing safety concerns,annoying flight delays,and even pollutions.Flight trajectories planning becomes one of the key generic enablers to fulfill performance objectives of next-generation air traffic management(ATM)systems for dealing with this situation.
According to a flight plan, flight trajectories planning initializes a reference trajectory in order to compel an aircraft into a planned trajectory so as to avoid potential conflicts and allow for some optimality with respect to a given business and efficiency need or environmental criterion.1,2Generally,it could be roughly classified into three generic categories.The first one is strategic-level trajectories planning,which meets the requirement of air traffic flow management(ATFM)to facilitate a safe and efficient operation of the ATM system through planning based on a network-wide view.3Trajectories are generated for future with a macroscopic-level description in this phase.The second category is pre-tactical planning.To realize one or several trajectories conflict-free during the whole journey before departure,it usually concerns adjusting the flight trajectory to avoid static obstacles and predicting possible conflicts with minimization objectives involving flying distance,travel time,or fuel consumption.4,5The third category concerns trajectories in a tactical level.It usually optimizes or predicts parts of the trajectories considering realtime situations by adjusting aircraft heading or velocity.Related topics include local confliction resolution,6target time control,7and so on.However,due to the lack of a full consideration of the overall airspace,short-term or local planning could bring a ‘domino effect”8and is used as a step following strategic-level trajectories planning.
Strategic-level trajectories planning is the scope of this paper.In this phase,large-scale flight trajectories within a given period of time,usually more than double-digit trajectories,are planned or optimized on a national scale such as in the United States,9French,10and China,11or on a continental scale like in Europe.12Its primal intent is for congestion smoothing and efficiency promotion through well-considered network operational planning.Under this scenario,existing papers proposed different kinds of strategies and network models.Early works mainly focused on flow optimization over a sector network.Mixed 0–1 integer programming models to minimize flight delays with constraints of airports and sector capacities were most common.9,13Delahaye et al.10and Zhang et al.11proposed multi-objective models to generate flight plans with minimum delay cost and congestion.Since these planning models failed to consider the detailed airspace complexity,it is too loose and macroscopical to simply ensure flight operation safety by hourly capacity constraints and congestion metrics.
With technological advances of navigation and communication,the concept of 4D trajectory based operation(TBO)have gradually become reality in next-generation ATM systems.In the case of strategic planning,flight trajectories,therefore,could be specif i ed to a sequence of 3D points as well as reliable and achievable timestamps at which a flight reaches these points,called target time of arrival(TTA),and constraints imposed over the TTA are referred as controlled time over(CTO).14Besides,trajectory information with greater precision and predictability15enables network-wide conflict management in the strategic phase.Therefore,instead of trying to satisfy sector capacity constraints like what macroscopic models do,recent works have been concerned on a microscopic representation of traffic without any pre-structured network.These advanced works are devoted to directly solve a potential spatial or temporal conflict occurring within a detection region(like a micro-square12or a cube16)between any two intersecting trajectories using different resolution strategies,such as flight level allocation,17flight routing allocation,8tuning departure times,12or a combination of them,18even by employing a futuristic air traffic paradigm.19
In reality,the en-route airspace is constituted by an intricate airway network(AN).The AN is designed to connect thousands of airports and ground-based infrastructures and navigational aids so that flights can follow a sequence of crossing waypoints(CWs)20throughout a travel.Although 4D flight trajectories planning is advanced compared to current methods to relieve the constraints of the AN in a sense that precise control and information a reutilized,for now,an AN structure is still required for large-scale 4DTs at the moment.Many works have been proposed using the AN to generate 4DTs with the purpose of strategic conflict management.21,22These papers utilized the same sequential conflict detection method based on a pairwise strategy which tests each pair of sampling points of two probed trajectories.Unfortunately,it is far more timeconsuming and conservative than just detecting the possible conflicting area.Nonetheless,the network structure does pose less challenges for the safety of an operation.23
To inherit the advantages of the conflict detection and the network structure,conflict regions are employed around the CWs of the AN and then utilized to de-conflict 4D en-route trajectories in this paper.Trajectories throughout the network are adjustable in four dimensions,but may inevitably cause an unfavorable growth of fuel costs and flight delays compared to original planning.Hence,it is important to simultaneously consider safety and efficiency issues when making a 4D flight trajectory plan.A bi-objective network-wide 4D flight trajectories planning(N4DFTP)optimization problem is formulated to reconcile this conflict by producing 4DTs in the whole network with minimum conflicts as well as trajectory modification costs.
In order to solve this large-scale,highly-complex,and biobjective problem effectively,this paper utilizes the framework of a memetic algorithm which incorporates the advantages of an evolutionary algorithm24–28and multiple local search operators,29and presents a multi-objective multi-memetic algorithm (MOMMA).Thenon-dominated sorting genetic algorithm II(NSGA-II)24is implemented as the global search in the MOMMA.To further reduce the spatio-temporal complexity among trajectories,a metric called trajectories interaction(TI)is defined to indicate the degree of interaction between trajectories.On the basis of this metric,three local search operators provide specific local improvements including rerouting,departure time and TTA tuning,and flight level adjustment,to separate highly related trajectories.The three concerted operators can deeply exploit the solution space and enable the algorithm to converge towards fitter solutions.Furthermore,MOMMA adopts the ideas of weighted fitness and simulated heating30for hybridization of local search operators to global operators.Finally,MOMMA is evaluated to be beneficial for solving the N4DFTP problem using a regionalsize AN and flight plan data in China.Afterwards,a national-size experiment applies a dynamic updating scheme,i.e.,sliding time window,to further reduce the problem complexity.It verifies the performance of MOMMA for its practical application under a TBO environment.
The rest of this paper is organized as follows.In Section 2,the network and the conflict detection model are introduced.Then,mathematical formulation of the N4DFTP problem is proposed.Section 3 elaborates the design of local search operators and the hybridization scheme of MOMMA.Experimental setups for two real network cases and evaluation of the algorithm performance are shown in Section 4.Finally,Section 5 concludes the paper and our future work.
2.Problem formulation
2.1.Network-wide conflict management model
The AN can be represented as a bounded regionS⊂R3as shown in Fig.1.Viewed vertically,it is divided into several flight levels.For each flight level,the horizontal surface is modeled as a directed graph where CWs and airports are indicated as nodes.Arcs represent airways,which are designed to connect airports and ground-based infrastructures and navigational aids.Each of these layered networks has aNvvertical spacing distance.
When flights flying in the airspace,their trajectories are interacting with each other.We assume that flights scrupulously follow their planned routes so that they may only encounter each other at CWs and surrounding areas.To resolve these upcoming events among flights,conflict detection should be carefully conducted.Therefore,a CW,used to be represented by a point,20is zoomed in as a circular region when solving conflict detection.This region works as a buffer zone surrounding a CW.In Fig.2,three flights are going to pass CW1from different routes.When the real-time linear distance between trajectoriesfiandfjis less than the safe separation standard ω,i.e., ∀t,s.t‖Pfi(t)-Pfj(t)‖2< ω,wherePfi(t)is the geographic coordinates offiat timet,they are considered to be in conflict with each other.Normally,Nv=1000 ft(1 ft=0.3048 m)and ω =5 n miles(1 n miles=1852 m)by default.
By conducting a series of calculations w.r.t.the intersecting trajectories,the practical separation standard,the cruising speed,as well as trajectory uncertainty,we could get a reasonable size,namely the radius of the conflict region CRk.Rkis defined as the following in this paper:
In addition,some special cases and our assumptions have to be emphasized when calculatingRk:
(1)One flight keeps the same cruising speed at different levels.
(2)Two adjacent CRs could overlap with each other while the CW of neither of them could locate within the other CR.
tion caused by the overlong Rk,we set
(5)In cases when a CW is configured only to sustain a single trajectory(as CW2in Fig.1),for the sake of separating flights using this route in the same direction,we still add a CR around this CW in these situations.
Hereby,the 4DT of a flight Trajfis defined in this paper as Trajf=is thekth conflict region of flightf,is the TTA when flightfentersflightfis inKfis a ordered set of the CRs(or airports)indexed sequentially by the order in which flightfflies over.The first and last indexes ofKfare airports.are the departure and arrival times,respectively.
Up to this point,the expected ideal outcome of strategiclevel conflict management by adjusting network-wide flight 4DTs is with only one flight residing in a given CR at a particular time-slot.This model computationally benefits from the elimination of pairwise distance computations.Aiming at resulting in a predictable conflict resolution in a macro level,this centralized way may reduce air traffic complexity in advance.
2.2.Mathematical optimization model
The network-wide 4D flight trajectories planning optimization problem could be described as follows:given an AN,the problem requires optimized 4DT planning for each flightfto minimize the total number of airborne conflicts and the trajectory modification cost simultaneously.Optimized planning should also guarantee that all airports and flights satisfy their capacity and performance limitations.Next,notations,decision variables,objectives,and constraints will be clarified.
2.2.1.Notation and decision variables
Expecting the notations mentioned in Section 2.1,Table 1 lists the definitions of rest of the required notations:
Particularly,two 0–1 variables are added as key decision variables.
2.2.2.Objective functions
The first and foremost objective to be minimized is the total number of conflicts.whereNt,k,l=which is the number of flights in CRkat levellat time-slott.
To avoid as many potential conflicts with other aircraft as possible,the reference trajectory of a flight could be significantly modified thus deviating far from its original plan.However,the cost of solving potential conflicts should be evaluated from an economical perspective.Essentially,we propose to minimize four parts of trajectory modification costs and maintain equity among modified flights.It can be expressed as
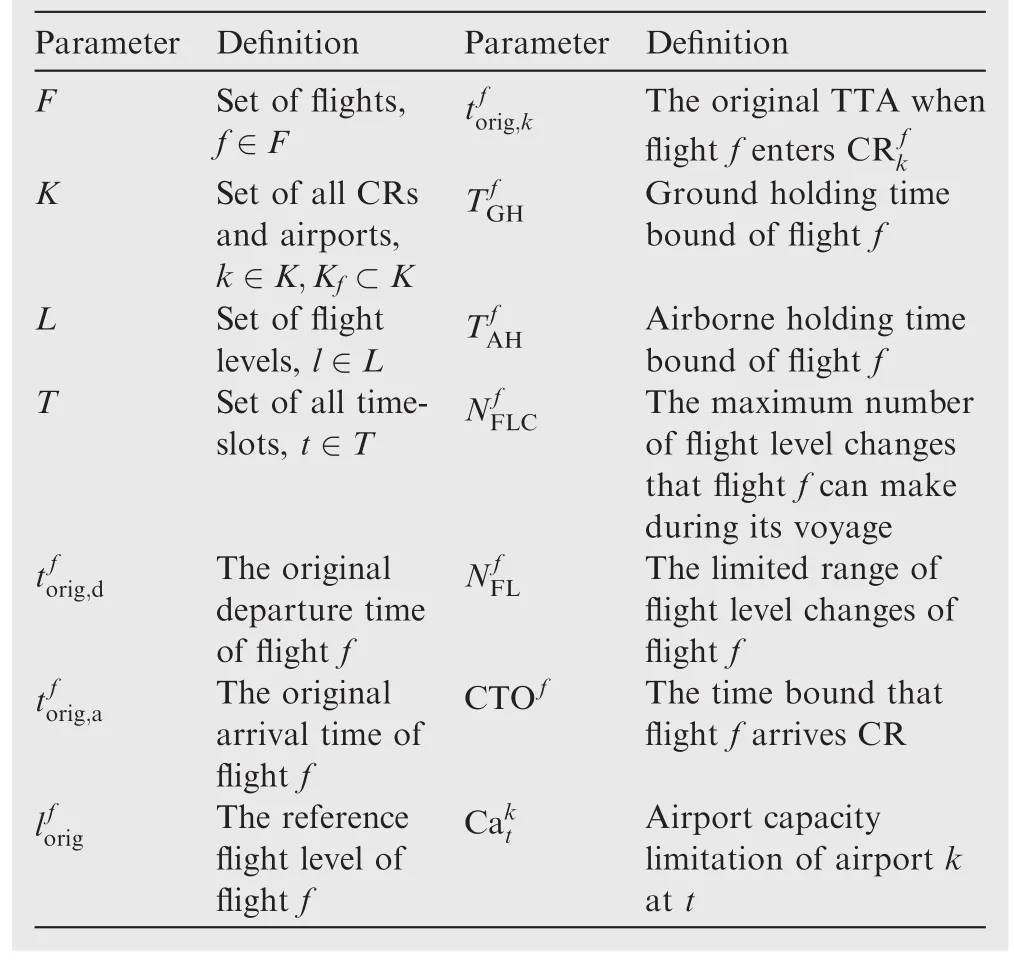
Table 1 Notations and definitions.
wherethefourpartsareCostGH=CostAH=holding,flight level change,or TTA control causes more fuel cost than applying no adjustment.In this paper,ground holding and airborne holding costs CostGHand CostAHare positively proportional to the holding time.30Flight level cost CostFLis defined to be related to the total number of level changes that flights should make along the entire phase.On the premise of aircraft performance allowance,a flight trajectory is allowed to make any times of flight level changes,and the corresponding cost will undergo an obvious increment.Time tuning cost is denoted as CostTTAand relevant to ttaf=If one of the TTAs of Trajfis different from its original TTA,then ttafequals 1.Similar to CostFL,when a TTA is going to be changed,flight crew has to take corresponding fuel-consuming actions(speed changing)which lead to a cost increment.Besides,although each part of the cost has a different definition,they should be normalized to the same cost unit,and decision makers could make their cost proportions close to the reality by utilizing the exponential proportional factorsp,q,andW.
2.2.3.Constraints
Considering efficiency,equity,and aircraft performance,each element in a trajectory should be as close as possible to their scheduled value.The model’s constraints sets are as follows:
The first two sets of constraints ensure that ground and airborne holding times will not exceed the upper bounds.Constraints in Eq.(6)stipulate that each flight can change its level at mosttimes during its voyage.Constraints in Eq.(7)claim that the range of level change should be within the range ofConstraints in Eq.(8)state the performance of a flight that it can only change to its neighbor level per time.The following constraints concern the TTA.Constraints in Eq.(9)guarantee the time continuity that a flight cannot arrive at CRkat timetif it is still in the preceding CR by timet.Constraints in Eq.(10)show the bounds of the TTA of each trajectory foreach CR.Eq.(11)are the airport capacity constraints,wherehasl=0,which means that flightfis either departing from or arriving at airportkat timet.The number of all the flights at airportkat timetwill not exceed
3.Multi-objective multi-memetic algorithm for N4DFTP
As introduced in Section 2,the N4DFTP problem is formulated as a bi-objective optimization problem with non-linear,non-continuous,and non-differentiable objective functions.Meanwhile,numerous coupled decision variables and constraints further complicate the problem,so that traditional optimization methods are not feasible.Fortunately,multiobjective evolutionary algorithms(MOEAs)appear to be promising alternatives for their ability in handling the aforementioned difficulties.However,directly applying an untailored MOEA into our specific problem might not be able to provide optimal solutions,since solely depending on the global search is inadequate.Consequently,enlightened by the merits of memetic algorithms(MAs)that incorporate the advantages of both global and local searches,in this paper,we propose a multi-objective multi-memetic algorithm(MOMMA)for the N4DFTP problem.
For the multi-objective problem,the neighbor generation strategy and acceptance criterion of local search are of great significance in the MA framework,which are specially designed in the MOMMA as demonstrated in the rest of this section.Furthermore,not just one but a set of local search operators is implemented in MOMMA as preferable complements to the global search.MOMMA can select from multiple local search operators for different search stages or individuals for a better performance.31Consequently,in addition to setting the frequency and intensity of the MA,the choice of an appropriate local search operator also exerts a great influence on MOMMA.32,33
Considering the problem characteristics and design issues mentioned above,a key problem-specific metric,i.e.,trajectories interaction(TI),is proposed to guide the selection of trajectories for problem complexity reduction.On the basis of TI,three specifically designed heuristic local search operators,whose functions are rerouting,time tuning,and flight level allocation,respectively,are integrated with NSGA-II for the N4DFTP problem.Moreover,for the purpose of establishing a good balance between explorative and exploitative traits,MOMMA integrates local search operators with the global operator by effective hybridization schemes which will be explained later.As the framework is shown in Fig.3,after the integration of local and global operators,the algorithm proceeds to update the population and iterates the procedure until the termination criterion is satisfied.In the following subsections,we will firstly introduce each operator in depth.Afterwards,the full details of MOMMA will also be described.
3.1.Local search operator design
3.1.1.Trajectories interaction(TI)
With the purpose of optimizing trajectories on the network level,MOMMA strives to relax the spatial-temporal interactions among all trajectories based on TI,which is a metric of the trajectories interaction.The interaction between flightsfiandfj,i.e.,φij,is defined as follows:
Note that φjiand φijmay not be equal.Matrix Φ = [φij]|F|*|F|is asymmetric.Summation of rowiof matrix Φ is a measurement of the interactions among all the flights,which indicates the total spatial-temporal overlap degree between these flights and flightfi,defined as TI value Φi=∑
j∈F{i}φij.If Φiof a flight is relatively large,its original trajectory should be changed.Especially,either holding this flight on the ground,controlling its TTA,letting it detour around the conflicting CR,or changing its flight level will reduce the TI values of the interacting flights and may also reduce its own TI value.
In order to eliminate conflicts in the whole network without inducing too much modification cost,MOMMA separates highly related trajectories in the 4D space with the purpose of achieving a better searching performance and a smaller searching span and depth on the basis of TI.Therefore,MOMMA sets a TI threshold ΦThto identify ‘who needs to be modified”,and only employs the following three local search operators to finish the issue of ‘how to be modified”,namely how to generate new neighbor solutions that have high opportunities to be accepted.
3.1.2.Rerouting local search
In rerouting local search(RLS),trajectories which have higher TI values than ΦThare selected into setFRLS,and then are sequentially detoured to other feasible routes which can get rid of at least one of the current conflicting CRs.The rerouting strategy is allowed for current operation,and will be broadly applied to flights in the future.In this operator,since detour must increase flight time,TTAs along the new route are adjusted to decrease the airborne delay cost,namely,the cruising speed is not constant anymore.
The advantage of this neighbor generation method is that it orderly applies local search on highly related trajectories and frees some other conflicting trajectories naturally.Moreover,the impact that comes from latter modified trajectories on completed trajectories is reduced.Unfortunately,the coupled relation of trajectories and the bi-objective nature of this problem explain the limitation of local search.Hardly can every time local search avoid generating a degenerated solution.Good results,however,will show up since a large number of populations are jointly evolving.
3.1.3.Time tuning local search
Controlling the TTA of a trajectory at a CW or specific waypoint is the main function of a 4D trajectory based operation in next-generation ATM systems.14In our work,this function is named time tuning local search(TTLS).Similar to RLS,after TTLS determines the set of modified trajectoriesFTTLSon the basis of a TI threshold,it sequentially calculates the minimum tuning time slotwhich can resolve the maximum number of conflicts of CRkcaccording to Eq.(13).In Eq.(13),kcis the index of the most conflicting CR withinKfandis the time slot that CRkcendures the largest number of conflicts.andare the time-slots whenfienters and exits CRkc,respectively.Ifis near the exit time,should be advanced,andequals to a maximum negative number that minimizes the total number of spatial-temporal overlaps within CRkcbetweenfiand all other flights inFTTLS.Conversely,should be delayed,andequals to a minimum positive number according to the second row of Eq.(13).Then,is tuned byas in Eq.(14).If the tuning slots violate Eq.(10),then TTLS turns to hold the flight on the ground attime-slots,which means that all the TTAs are slided correspondingly.
3.1.4.Level adjustment local search
In a realistic ATM operation,airspace is divided into several flight levels which are used by flights from different heading directions to prevent face-to-face conflicts. Previous papers17,18,21proposed a level allocation strategy which usually confined a flight even a flow to only one level all along the travel.It is far from the reality that an aircraft is able to change its flight level to avoid conflicts many times if the aircraft performance allows,as shown in Fig.4.AoandAddenote original and departure airports of illustrated flights.The reference flight level(RFL)off1andf2are all FL280 butf1modif i es to FL300 after it passes CW1.
Therefore,equivalent to the previous local search operator,trajectoriesf∈FLALSare executed with different adjustments for conflict avoidance according to its current status as in Eq.(15):
(1)If the current trajectory has no level change,let it adjust the level before CRkcand keep flying over the new level.
(2)If the current flight plan has a level change,and if kcis before its current adjusting point ka,let it adjust the level before kcand keep flying over the new level.
(3)If the current flight plan has a level change,and if kcis at or after ka,let it adjust the level after kcand keep flying over the new level.
To decrease the problem complexity and abide by the operation reality,flight trajectories are strictly constrained by Eqs.(6)–(8).In this way,only flight levels and the names of changing CRs need to be recorded.Besides,in the consideration of strategic-level planning,vertical conflicts happen when climbing and descending are ignored.Therefore,we assume that all flights adjust flight levels before arriving at the next CR.
3.2.Hybridization of local search operators
To reach a favorable hybridization of local search operators,two main issues need to be solved beforehand.The first issue is finding an appropriate choice,frequency,and intensity of local search to avoid pre-mature convergence,diversity loss,and resource waste.32Since different local search operators in MOMMA have different functions for guiding search to different areas of the solution space,three coevolving local search operators should be chosen carefully to control the resource waste.32
The second issue to be considered is,for local search in multi-objective optimization,how to reach an effective acceptance criterion(the criterion of whether accepting a generated neighbor solution or not).A bad acceptance criterion might disperse solutions generated to undesirable regions or debilitate the effects of local search operators.34
In lights of the above-mentioned design issues of local search operators,this paper proposes to use a weighted vector to control the choice,frequency,and acceptance criterion in a more compact way,where the two objectives are unif i ed and the three local search operators are integrated according to the weighted vector.Besides,we apply simulated heating,which is a non-linear process to guide the intensity setting of local search for the best result.
3.2.1.Weighted vector
In a single-objective MA,the objective function itself,is most widely used to determine the acceptance of a neighbor solution.In multi-objective optimization,things are quite different.A weighted vector is defined as λ = [λ1,λ2], where λ1=rand(0,1)and λ2= (1- λ1)for the two objectives respectively.35The two normalized objectives are weighted to be a single fitness function for making an acceptance decision by
For each population,the weighted vector is randomly updated.A memetic offspring Popneighbor,which is generated by local search,is accepted as long as its weighted-sum fitness is less than fitness(λ,Pop).More than just generating an acceptance criterion,the choice and frequency of local search in the MMA could be controlled through setting varying weighted vectors λ.Because the N4DFTP problem has two conflicting objectives,the local search operators mainly aim to decrease conflicts but sacrif i ce the cost.Considering the fact that rerouting flight causes the highest modification cost,while LALS and TTLS cost least,MOMMA usestrol the choice andfrequency.When λ is too close to the conflict-axis,an offspring solution may have a seriously degraded cost value.When λ is near the cost-axis,the operators only keep a non-dominate solution.Thus,through carefully setting the range of λs for the three local search operators,we can define the proportion of the population of size μ that undergoes effective local search in MOMMA and get the result we have expected.
3.2.2.Simulated heating
Since each step of local search is supported by problem-specific knowledge,local search operators are more effective but more costly.36Consequently,intensity is set to control the maximum computational budget allowable for local search to expend on improving a single solution.In this paper,intensity is defined as a function of the generation that has a changing slope,interpreted as Simulated Heating(g)shown in line 4 of Table 2.This function describes the process during which since the inception of the memetic evolution,local search has a low searching accuracy.Hence,local search puts low efforts which means that Simulated Heating(g)is small and accepts a generated neighbor quickly.After MOMMA locates the possible optimal searching area,it is reasonable to increase the intensity to improve the solution quality.The deepness and accuracy of local search gradually grow along with the increase of Simulated Heating(g).
Finally,the Pseudo-code of local search is given in Table 2,which especially emphasizes on the procedure controlled by the hybridization schemes in Sections 3.2.1 and 3.2.2.

Table 2 Pseudo-code of local search operator.
3.3.Full details of MOMMA
As essentially being a multi-objective metaheuristic,global search in MOMMA should demonstrate satisfactory performance on the multi-objective problem.NSGA-II presented in Ref.24 is one of the superior algorithms whose global operators were applied for its good performance on elitist selection,dominance ranking,and diversity maintenance.MOMMA starts with initializing a population randomly within the constraints.At each iterationg,populations are updated by global operators and local search operators.This procedure repeats until the maximum generation MaxGen is reached.
3.3.1.Genetic encoding
The decision variables are directly encoded into a solution chromosome.A chromosome of length |F|represents an operational plan for all trajectories in the airspace;a gene on the chromosome represents a trajectory’s operational plan Trajf,and its detailed structure is shown below:
whererfis the route number that Trajfflies.Oncerfis selected,|Kf|is then given.ka1tokaNFLCis the first to theNFLCth level adjusting point.Encoding is also supplemented by the TI values of each flight corresponding to the whole chromosome as well.
3.3.2.Genetic operators
It can be expressed as G:Popμ(g)↦Popβ(g).A number of μ individuals Popμattend tournament selection and crossover and mutation operations with parameters including the size of the mating poolQand the crossover and mutation probabilitiesPcandPm.β offsprings Popβ(g)are produced as a result.
(1)Crossover is essentially a random and multiple-point operation.For each gene,it has the same chance to inherit the gene from one of its two parents.
(2)For each gene,if it satisfies the mutation probability,its value will be randomly changed by a given value within constraints.
3.3.3.Constraint handling
No guarantee can be made that genetic and local search operators could always generate feasible solutions.If any violation happens on one gene,it will be set to a closest boundary value of the corresponding set according to Eqs.(4)–(11)except Eq.(6).Constraints in Eq.(6)are guaranteed by the encoding structure in Section 3.3.1.
3.3.4.Updating operators
The elitism strategy is used for updating,expressed as U:Popμ(g)× Popβ(g)× Popγ(g)↦Popμ(g).After local search updates γ offsprings from β genetic offsprings,an updating operator combines the genetic and memetic offsprings.Then it allows them to compete with their parents Popμ(g)and archives survivals according to dominance relations and crowding distance.24In this way,the procedure repeats to generate the subsequent generation.
Finally,Table 3 demonstrates the pseudo-code of MOMMA.

Table 3 Pseudo-code of MOMMA.
4.Empirical study
In order to verify the effectiveness of MOMMA for solving the N4DFTP problem,comprehensive computational experiments are firstly carried out on a regional-size network.Subsequently,the application value of MOMMA for a practical operation is tested by a national-size network.The realworld domestic flight plan data of China we used were extracted from a flight schedule database(data courtesy:Aviation Data Communication Corporation,Beijing)on December 3rd,2015 from 0800-1200,and the real operation was late to 1700,which means that an operation with a nearly 9-hour long duration required planning.
The first experimental case is a regional-level network,captured in the Northern China and shown in a small yellow box in Fig.5.It includes 50 airports,more than 700 CWs,and 12 flight levels.334 flights departure during that time are involved.The second experimental case represents the problem concerning the nation-wide network in China.The flights planning during the operation time horizon contains 1927 scheduled flight plans.Fig.5,as a whole,illustrates the airspace of China which includes198airports and more than 1500 CWs.The algorithms were all implemented in C++,and the experiments were performed on a Windows Server with 2.10 GHz CPU and 16 GB of RAM.All the outcomes were collected on the basis of 10 independent runs.To normalize each part of Eq.(3)which has different definitions for the same cost unit,the problem parameters are set asp=1,q=3,MGH=2,MAH=2,MFL=3,MTTA=2,TS=20 s to conform the model to the reality of Chinese conditions and the survey of airline costs.38
4.1.Regional-size case
In this subsection,to verify the effectiveness of MOMMA and multiple local search operators,we present three computational experiments.First of all,parameter sensitivity analysis will be conducted to bolster that the following resulted performance is achieved with the best parameters.Next,we will demonstrate the non-dominated solutions and numerical results of MOMMA compared with those of NSGA-II and MAs with single local search.Moreover,the hybridization scheme of MOMMA will also be compared with those of other existing strategies.
4.1.1.Parameter sensitivity analysis
In the consideration of maintaining a reasonable computation consumption for the N4DFTP problem,the population size and maximum generation are configured empirically10asshown in Table 4.In MOMMA,other algorithm parameters explained in tions 3.2 and 3.3 are well-tuned according to the sensitivity analysis shown in Fig.6,where the average hypervolume metricIH39is recorded to assess the overall equality of solutions.For each parameter setting in Fig.6,the one that results in the highestIHis selected and recorded in Table 4.For optimization perspective,a satisfied TI threshold ΦThis expected to reduce searching blindness and better control the neighborhood range.A low ΦThwill lead to an oversize neighborhood and resource waste.In that case,ΦTh=0.015 is better for controlling the size of a generated neighborhood for the individual size like our instance.30

Table 4 Parameters of MOMMA.
4.1.2.Effectiveness of MOMMA
The average values of minimum total conflicts to the evolution of generations are plotted in Fig.7.The four compared algorithms are setup with the same evolutionary parameters as those of MOMMA,exceptThe declining curves in Fig.7 illustrate that the MAs can clear up conflicts more quickly than NSGA-II which possesses no local search operator,and thus demonstrates the effectiveness of the local search operators on eliminating conflicts throughout the considered airspace.With the same initialization,MOMMA drags the total conflicts down to zero early around 100 generations thanks to the local search operators using the problem-specific knowledge and the conflict avoidance strategies.However,without the help of local search operators,NSGA-II fails to accomplish conflict-free trajectories plans all along the evolutions as it is stuck with achieving a tradeoff between the two objectives.
In fact,NSGA-II with single local search works well to find a conflict-free solution as MOMMA does.However,to cope with the multi-objective N4DFTP problem,the reason why using multiple local search operators is clear when comparing the performance between MOMMA and the aforementioned algorithms.From Fig.8,we can see that MOMMA outperforms the others on effectiveness for fitter solutions.From the figure,MOMMA shows superior performance on the flight trajectory cost.Although the other three MAs also achieve conflict-free solutions,yet via checking the vertical direction,they sacrif i ce too much on trajectories costs.As single local search only focuses on one kind of adjustment strategies,it is more likely to be trapped in the local optimum.Therefore,thanks to the reasonable hybridization of three local search operators,MOMMA dominates in both directions in the figure and provides a promising tradeoff between the two objectives.

Table 5 Average values of Δ,ID,and IH.
Besides the direct perception from Fig.8,a quantitative evaluation is also shown in Table 5.Normalized objective vectors were used to compute three favorable metrics to assess the performance of multi-objective algorithms,which areIH,the spread(Δ),24and the distance from the reference set(ID).40Δ implies the distribution of non-dominated solutions.IDreflects the closeness of the given set to the reference set which is constituted by the non-dominated solutions of all compared solutions.The superior one among the five algorithms will have the largestIH,while with the smallestIDand Δ.24,39,40In Table 5,the optimal values are in boldface and the corresponding standard deviations are enclosed in brackets.In terms of these three metrics,MOMMA achieves a relatively better performance as it has better metrics values and similar deviations compared to the other four algorithms.
4.1.3.Comparing MOMMA with different hybridization strategies
The acceptance criterion is one of the major issues in the design of multi-objective MAs.To investigate this issue,we have compared the aggregation strategy used in MOMMA with two other acceptance criteria which are brief l y described as follows:
(1)Biased strategy:Hunger for a conflict-free solution,the biased strategy only accepts a new neighborhood solution if the value of total conflicts is less than that of the current solution.
(2)Greedy strategy:On the basis of a dominance relation,the idea is to accept a new neighborhood solution if it dominates the current solution.
Fig.9 depicts the non-dominated solutions of the three compared strategies.The biased strategy indeed can disperse a solution to the desired regions of the Pareto front.However,it neglects the bi-objective nature of the problem.Being a dominance-based acceptance criterion,the greedy strategy may also have significant disadvantages.Considering the fact that local search operators are mainly focused on resolving conflicts,the greedy strategy can therefore hardly accept any neighborhood solutions and result in the waste of computation resources.Therefore,the results of the greedy strategy are similar to those of NSGA-II.
Next,we will compare simulated heating with two other intensity schemes to verify that the intensity setting we adopted is also effective and efficient.The standard hybridization scheme has the same computational time consumption as that of simulated heating but a constant intensity.The other one applies high intensity throughout the evolution process,which is called aggressive scheme.From Fig.10,local search operators hybridized by the simulated heating scheme outperform the others.
4.2.National-size case
It is significant to testify the performance of MOMMA on solving a practical application problem which consists of trajectories over the whole AN of China for a long period time.If we run MOMMA directly on all of these trajectories with the same generation as in the regional-size case,the algorithm has still not converged needless to mention the prohibitive computation time.As a consequence,we reduced the problem complexity by using a dynamic updating scheme called sliding time window.MOMMA only considers flights that are scheduled to take off between the start time to the nextTWminutes in the future.Particularly,in a short time window,operation environment prediction could be regard as deterministic.
The detailed method is that if a trajectory plan needs to be delayed beyondTW,it will be added and then be re-optimized in the next window.Only the conflict-free solution is computed in the next window.Aircraft that are still airborne in the nextTWare considered in the computation of total conflicts of the whole operation time,but no adjustment can be made any more.In our experiment,4-h flight plans are decomposed into 8 windows withTW=30 min.Accordingly,within each time window,there are 321,215,195,221,227,270,253,and 225 4DTs need to be planned respectively.Parameters settings thereby do not need to be changed since each window is comparable to the size of the prior case.Besides,MOMMA spends 1925 s average computation time for the regional case.Each window of the national case experiment could finish in no more than this time,and the average total computation time it requires is only 11896 s.This observation demonstrates that the introduction of a sliding window does satisfy the demand of strategic-level trajectories planning.
For the sake of concision,only 4 graphs of the nondominated solutions are shown in Fig.11.The start times of each 30 min window are 8:00,9:00,10:00,and 11:00,respectively.Along with the sliding of the time window,the numbers of airborne trajectories are increasing but the number of adjustable trajectories is limited.Clearly,MOMMA is still demonstrated to be more effective than NSGA-II.However,it is concluded that even the number of planning trajectories is comparable,more trajectory costs have to be spent for finding conflict-free solutions with the sliding window according to Fig.11.Thanks to the three local search operators,MOMMA decreases the total conflicts in the perspective of strategic-level trajectories planning from 12450 to 0 compared to the original plan.It only has an average trajectories modification cost(conflict-free solutions)of 8212 overall.Therefore,it is reasonable and effective to introduce the 4DT and corresponding trajectory adjustment strategy in MOMMA for a more efficient and safe air traffic operation in the future.
Another observation is that MOMMA caters to another operational need of the industry.Decision makers expect to resolve more conflicts with less modified trajectories and reasonable costs.Table 6firstly demonstrates the average proportions of modified trajectories.As we can see,the performanceof MOMMA exceeds that of NSGA-II in the percentages of trajectories that contain both modified routes and modified departure times.The percentages of trajectories that have modified routes and departure times of MOMMA are all lower than those of NSGA-II.This is resulted from the fact that the local search strategy intensif i es the modification on trajectories involved in more conflicts.For MOMMA,it decreases the number of ground holding flights,some of which are turned to precisely control their TTAs and change their flight levels.This feature ensures that aside from the aforementioned superiorities of MOMMA,it can also maintain comparable trajectory cost and ground and airborne holding times as with those of NSGA-II.

Table 6 Comparison between MOMMA and NSGA-II.
5.Conclusions and future work
This paper investigated an N4DFTP model for strategic planning of 4D flight trajectories with the aims of minimizing total conflicts and flight trajectory costs.A systematic approach,MOMMA,which is an effective problem-specific approach based on the MA framework,was proposed to solve N4DFTP by rerouting,time tuning,and level allocation.With the idea of heuristically reducing the interactions among flight trajectories,metric TI was proposed and utilized by three local search operators in MOMMA to ensure deep exploitation of the problem-specific structure and convergence toward fitter solutions.Besides,MOMMA systematically hybridized three local searches with a global search by applying weighted sum fitness and simulated heating strategies.Several experiments were designed and implemented based on real data of the Chinese airspace and flight trajectory plans.The regional-size case demonstrated the superiority of MOMMA and verified the effectiveness of the proposed local search hybridization scheme for the N4DFTP problem.From the practical viewpoint,a size comparable to the entire network of China can be solved within reasonable computation time by a sliding window technique,and the solutions meet the operational requirement.
Although preliminary results are promising,the problem model was on account of several strict assumptions we made and situations we ignored,such as flight cancellation and continuous flight in reality.In the future,it is also necessary to compare 4D trajectories with all national-wide detailed actual operation track data,and validate our trajectories planning in a real operation to get more convincing results.Besides,we deem that for solving multi-objective optimization and under the framework of a meme-inspired algorithm,the design of true memetic local operators based on TI,and the synergistic effect between local search operators and global search could be further promoted from the current static way to memetic automaton and adaptive hybrids in future studies.29
Acknowledgements
This study was co-supported by the National Science Foundation for Young Scientists of China(No.61401011),the National Key Technologies Ramp;D Program of China(No.2015BAG15B01),and the Foundation for Innovative Research Groups of the National Natural Science Foundation of China(No.61521091).
1.Delahaye D,Puechmorel S,Tsiotras P,Feron E.Mathematical models for aircraft trajectory design:a survey.Lecture Notes Electr Eng2013;290:205–47.
2.Bongiorno C,Gurtner G,Valori L,Lillo F,Mantegna RN,Micciche`S,et al.An agent based model of air traffic management.Proceedings of the 3rd SESAR innovation days;2013 Nov 26–28.Stockholm,Sweden.Brussels:EUROCONTROL;2013.
3.ICAO manual on collaborative air traffic flow management[Internet].Chicago:ICAO;2014.Available from:http://www.icao.int/airnavigation/IMP/Documents/9971%20Collaborative%20Flight%20and%20Flow%20Informaiton.pdf[cited 2016 June 7].
4.Dougui N,Delahaye D,Puechmorel S,Mongeau M.A lightpropagation model for aircraft trajectory planning.J Global Optim2013;56(3):873–95.
5.Soler M,Zou B,Hansen M.Flight trajectory design in the presence of contrails:application of a multiphase mixed-integer optimal control approach.Transp Res C:Emerg Technol2014;48:172–94.
6.Treleaven K,Mao ZH.Conflict resolution and traffic complexity of multiple intersecting flows of aircraft.IEEE Trans Intel Transp Syst2008;9(4):633–43.
7.Margellos K,Lygeros J.Toward 4-D trajectory management in air traffic control:a study based on Monte Carlo simulation and reachability analysis.IEEE Trans Control Syst Technol2013;21(5):1820–33.
8.Ruiz S,Piera MA,Nosedal J,Ranieri A.Strategic de-confliction in the presence of a large number of 4D trajectories using a causal modeling approach.TranspResC:EmergTechnol2014;39:129–47.
9.Zhang W,Kamgarpour M,Sun D,Tomlin CJ.A hierarchical flight planning framework for air traffic management.Proc IEEE2012;100(1):179–94.
10.Delahaye D,Sof i ane O,Puechmorel S.Airspace congestion smoothing by multi-objective genetic algorithm.Proceedings of the 2005 ACM symposium on applied computing;2005 Mar 13–17;Santa Fe(NM).New York:ACM;2005.p.907–12.
11.Zhang XJ,Guan XM,Zhu YB,Lei JX.Strategic flight assignment approach based on multi-objective parallel evolution algorithm with dynamic migration interval.Chin J Aeronaut2015;28(2):556–63.
12.Nosedal J,Piera MA,Ruiz S,Nosedal A.An efficient algorithm for smoothing airspace congestion by fine-tuning take-off times.Transp Res C:Emerg Technol2014;44:171–84.
13.Bertsimas D,Lulli G,Odoni A.An integer optimization approach to large-scale air traffic flow management.Oper Res2011;59(1):211–27.
14.SESAR concept of operations-deliverable D3[Internet].Brussels:EUROCONTROL;2014.Available from:https://www.eurocontrol.int/sites/default/f i les/field_tabs/content/documents/sesar/20070717-sesar-conops.pdf[cited 2016 June 7].
15.Wandelt S,Sun XQ.Efficient compression of 4D-trajectory data in air traffic management.IEEE Trans Intel Transp Syst2015;16(2):844–53.
16.Ruiz S,Piera MA.Relational time-space data structure to enable strategic de-confliction with a global scope in the presence of a large number of 4d trajectories.J Aeros Oper2013;2(1):53–78.
17.Barnier N,Brisset P.Graph coloring for air traffic flow management.Ann Oper Res2004;130(1):163–78.
18.Chaimatanan S,Delahaye D,Mongeau M.A hybrid metaheuristic optimization algorithm for strategic planning of 4D aircraft trajectories at the continental scale.IEEE Comput Intell M2014;9(4):46–61.
19.Prot D,Rapine C,Constans S,Fondacci R.A 4D-sequencing approach for air traffic management.Eur J Oper Res2014;237(2):411–25.
20.Cai KQ,Zhang J,Zhou C,Cao XB,Tang K.Using computational intelligence for large scale air route networks design.Appl Soft Comput2012;12(9):2790–800.
21.Allignol C,Barnier N,Gondran A.Optimized vertical separation in Europe.Digital avionics systems conference(DASC);2012 Oct 14–18;Williamsburg(VA).Piscataway(NJ):IEEE Press;2012.p.1–81.
22.Guan XM,Zhang XJ,Han D,Zhu YB,Lv J,Su J.A strategic flight conflict avoidance approach based on a memetic algorithm.Chin J Aeronaut2014;27(1):93–101.
23.Gurtner G,Bongiorno C,Ducci M,Micciche`S.An empirically grounded agent based simulator for the air traffic management in the SESAR scenario.J Air Transp Manage2017;59:26–43.
24.Deb K,Pratap A,Agarwal S,Meyarivan T.A fast and elitist multi-objective genetic algorithm:NSGA-II.IEEE Trans Evol Comput2002;6(2):182–97.
25.Du WB,Gao Y,Liu C,Zheng Z,Wang Z.Adequate is better:particle swarm optimization with limited-information.Appl Math Comput2015;268(1):832–8.
26.Gao Y,Du WB,Yan G.Selectively-informed particle swarm optimization.Sci Rep2015;5:9295.
27.Dorigo M,Maniezzo V,Colorni A.Ant system:optimization by a colony of cooperating agents.IEEE Trans Syst Man Cybern Part B:Cybern1996;26(1):29–41.
28.Storn R,Price K.Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces.J Global Optim1997;11(4):341–59.
29.Chen XS,Ong YS,Lim MH,Tan KC.A multi-facet survey on memetic computation.IEEETrans Evol Comput2011;15(5):591–607.
30.Yan S,Cai KQ,Zhu YB.A multi-objective memetic algorithm for network-wide flights planning optimization.Proceedings of 2015 IEEE27thinternational conferenceontools withartificial intelligence(ICTAI 2015);2015 Nov 9–11;Vietri sul Mare,Salerno,Italy.Washington,D.C.:IEEE Computer Society;2015.p.518–25.
31.Krasnogor N,Blackburne B,Burke EK,Hirst JD.Multimeme algorithms for protein structure prediction.In:Merelo Guervo´s JJ,AdamidisP,BeyerH-G,Ferna´ndez-Villacan˜asMartı´nJL,Schwefel H-P,editors.Proceedings of the 7th international conference on parallel problem solving from nature-PPSN VII;2002 Sep 7–11;London.Berlin:Springer;2002.p.769–78.
32.Sindhya K,Miettinen K,Deb K.A hybrid framework for evolutionary multi-objective optimization.IEEETransEvol Comput2013;17(4):495–511.
33.Ong YS,Keane AJ.Meta-lamarckian learning in memetic algorithms.IEEE Trans Evol Comput2004;8(2):99–110.
34.Jaszkiewicz A,Ishibuchi H,Zhang Q.Multi-objective memetic algorithms.Handbook of memetic algorithms.Berlin:Springer;2012.p.201–17.
35.Jaszkiewicz A.Genetic local search for multi-objective combinatorial optimization.Eur J Oper Res2002;137(1):50–71.
36.Nguyen QH,Ong YS,Lim MH.A probabilistic memetic framework.IEEE Trans Evol Comput2009;13(3):604–23.
37.Airtopsoft.com[Internet].Brussels:Airtopsoft S.A.;2014.Available from:http://www.airtopsoft.com/[cited 2016 June 9].
38.European airline delay cost reference values[Internet].Brussels:Eurocontrol;2014.Available from:http://www.eurocontrol.int/sites/default/f i les/publication/f i les/european-airline-delay-cost-reference-values-final-report-4-1.pdf[cited 2016 June 7].
39.Zitzler E,Laumanns M,Thiele L.SPEA2:improving the strength pareto evolutionary algorithm.Proceedings of evolutionary methods for design optimization and control with applications to industrial problems;2001 Sep 19–21;Athens.Barcelona:CIMNE;2001.p.95–100.
40.Czyzak P,Jaszkiewicz A.Pareto simulated annealing–a metaheuristic technique for multiple-objective combinatorial optimization.J Multi-Criteria Decision Anal1998;7(1):34–47.
7 June 2016;revised 12 September 2016;accepted 24 November 2016
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Review on signal-by-wire and power-by-wire actuation for more electric aircraft
- Real-time solution of nonlinear potential flow equations for lifting rotors
- Suggestion for aircraft flying qualities requirements of a short-range air combat mission
- A high-order model of rotating stall in axial compressors with inlet distortion
- Experimental and numerical study of tip injection in a subsonic axial flow compressor
- Dynamic behavior of aero-engine rotor with fusing design suffering blade of f
