Exploiting global information in complex network repair processes
2017-11-20TianyuWANGJunZHANGSebastianWANDELT
Tianyu WANG,Jun ZHANG,Sebastian WANDELT
School of Electronic and Information Engineering,Beihang University,100083 Beijing,China Beijing Key Laboratory for Network-based Cooperative ATM,100083 Beijing,China
Exploiting global information in complex network repair processes
Tianyu WANG,Jun ZHANG,Sebastian WANDELT*
School of Electronic and Information Engineering,Beihang University,100083 Beijing,China Beijing Key Laboratory for Network-based Cooperative ATM,100083 Beijing,China
Available online 20 April 2017
*Corresponding author at:School of Electronic and Information Engineering,Beihang University,100083 Beijing,China.
E-mail address:wandelt@buaa.edu.cn(S.WANDELT).
Peer review under responsibility of Editorial Committee of CJA.
Production and hosting by Elsevier
http://dx.doi.org/10.1016/j.cja.2017.03.007
1000-9361©2017 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.
This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
Robustness of complex networks has been studied for decades,with a particular focus on network attack.Research on network repair,on the other hand,has been conducted only very lately,given the even higher complexity and absence of an effective evaluation metric.A recently proposed network repair strategy is self-healing,which aims to repair networks for larger components at a low cost only with local information.In this paper,we discuss the effectiveness and efficiency of self-healing,which limits network repair to be a multi-objective optimization problem and makes it difficult to measure its optimality.This leads us to a new network repair evaluation metric.Since the time complexity of the computation is very high,we devise a greedy ranking strategy.Evaluations on both real-world and random networks show the effectiveness of our new metric and repair strategy.Our study contributes to optimal network repair algorithms and provides a gold standard for future studies on network repair.
©2017 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
Complex network;
Global information;
Greedy ranking;
Optimality;
Self-healing
1.Introduction
Many systems can be modeled as complex networks,where nodes represent elements of a system and links represent the relationship between elements.Examples include,but are not limited to,social,1,2economic,3,4traffic,5–7biological,8,9and technological networks.10,11Complex networks are often vulnerable under disruptions,e.g.,those caused by natural disasters or human intentional attacks.12,13Therefore,research on network robustness and resilience has gained significant attention.14,15Most researchers focus on network robustness,aiming to simulate network percolation processes;with the result that networks are often rather vulnerable.16–19One example of high-impact network failures is the power grid break-up in Northeast of the U.S and parts of Canada on August 14th,2003,which resulted from only a few power station failures.Another example is the air transportation delay occurred in Beijing on July 21st,2012 caused by a rainstorm,which led to a widespread cascading failure of air traffic.Small events can lead to wide-ranging(cascading)failures.
Network repair,the inverse problem of network attack,is less studied,albeit the quick recovery of network functionality is a tremendous challenge.During a network disruption,either nodes or links can be attacked.Similarly,for network recovery,new links can be added between unaffected nodes,or damaged nodes can be repaired.20,21After a careful review of relevant research,we find that most researchers have chosen to attack nodes in a network and then repair the network by adding links,mostly because adding links between existing nodes should be much easier than building a new node.Under realistic conditions,attacked nodes are often disabled forever,or even though they can recover from damage,the process is very time-consuming,during which the whole network would be influenced significantly.Therefore,the problem we study here is that under a disruption,nodes in the networks would be attacked,and in the recovery process,links are generated between surviving nodes.
In this paper,we discuss a very recently proposed network repair strategy,self-healing.22This strategy repairs networks only using local information with the goal to obtain a larger size of the giant component(GC-size)and at the same time to limit the cost of the repair.The cost here is defined to be the sum of the shortest path lengths of the added links in the original network,and this definition is used in the evaluation section in our paper.However,this twofold goal of self-healing makes it a multiobjective optimization problem.Thus far,the optimality of self-healing has not been analyzed,i.e.,the question is,how much does the exploitation of local information affect the repair quality?Motivated by this point,we propose a shortest-path related network repair evaluation metric.The new evaluation metric is based on the shortest path lengths(SPLs)of all node pairs in the network.In the new evaluation metric,the shortest path length between two nodes from different components is defined,since in the traditional complex network theory,the shortest path length exists only between two connected nodes,no matter they are connected directly or indirectly.Besides,because of its constraint that only local information is needed,selfhealing may not guarantee the repair quality.To assess the limitation of self-healing,global information is exploited in a new greedy ranking repair strategy.Experiments on real-world and random networks show that the new metric can evaluate the optimality of self-healing very well,and that the greedy ranking repair strategy restores networks’functionality in terms of the new metric.
The major contributions of this paper are summarized as follows:
(1)We discuss the optimality of a recent network repair strategy,self-healing.Motivated by the limitation of self-healing,we create a new shortest-path related evaluation metric of network repair,which can measure the connectivity between all node pairs.
(2)Based on the new evaluation metric,we propose a greedy ranking repair strategy,and provide an efficient implementation.
(3)We evaluate the optimality of self-healing and the effectiveness of our strategy on six real-world networks and three kinds of random networks.Our results show that self-healing’s optimality can be substantially improved in terms of the new metric.
This paper is structured as follows.In Section 2,we introduce the recently proposed network repair strategy,selfhealing.The limitation of this repair strategy is also discussed in this section.In Section 3,evaluation metrics of network repair are presented.A new evaluation metric and a greedy ranking strategy are proposed,and we make an improvement on the general strategy.In Section 4,both the optimality of self-healing and the effectiveness of our strategy are evaluated on six different real-world networks and three kinds of random networks.The conclusions and future work of this paper are presented in Section 5.
2.Self-healing
In this section,both the details and limitation of self-healing will be discussed.An introduction of self-healing is presented in Section 2.1.The limitation is classified into three aspects:non-deterministic network repair(Section 2.2);constraints of local information and the shortest path length(Section 2.3);redundancy of ineffective links(Section 2.4).
2.1.Introduction of self-healing
Self-healing is a very recently proposed strategy to repair complex networks.This strategy detects the level of the damage only relying on local information accessible to each node(its degree),and makes new connections with low cost.Therefore,in self-healing,each surviving node decides by itself whether it needs to generate a new link with another node.The process of self-healing can be divided into three parts:
(1)An original network,the number of nodes to be attacked,and two thresholds p and rmaxshould be given.For each surviving node,the original degree korigand the degree after attack kdamof each node should be recorded.p is the threshold for the fraction of remaining neighbors,and each node observes whether the fraction of its neighbors is less than this threshold.rmaxmeans the limitation of the new links’distance.
(2)For each surviving node,the value q=kdam/korigshould be recorded,and if q<p,the node is supposed to select a surviving node randomly to generate a new link.
(3)For each new link,only if its distance(the shortest path length in the original network)is no longer than rmax,the link would be finally generated.
In Fig.1,the process of self-healing on an example network is shown.Fig.1(a)shows an attack of two nodes on the example network;Fig.1(b)shows the network after the attack;the orange link in Fig.1(c)is the added link with self-healing under the best condition at a probability of 10%,while there would be no link to be added at a probability of 90%(the parameters of self-healing here arep=0.5 andrmax=2);Fig.1(d)presents one of the possible results with selfhealing,whilep=0.8 andrmax=3.The settings of the parameters in Fig.1(c)are the same as those used in the evaluations in a self-healing paper,22and are also used in the following evaluations of this section.
An obvious advantage of self-healing is that it can repair networks very fast because only local information is needed.However,at the cost of a good response speed,the quantity of self-healing could not be guaranteed in terms of its evaluation metrics.
2.2.Non-deterministic network repair
Because of the limitation of self-healing,when one node decides to generate a new link,it can only select a surviving node randomly from the network.This selection criterion leads to very non-deterministic results,which makes it confusing to identify whether a result is effective or not.To prove the randomness of self-healing,self-healing is evaluated on the same network(celegansneural,introduced in Section 4.1)for ten times to see how unstable the number of links and the cost of the repair are,when the attack range changes.Here,the attack range means the percentage of the number of attacked nodes out of the total number of original network nodes,and the rest of this paper uses attack range with the same meaning.
Self-healing repairs the same network(celegansneural)for ten times when the attack range varies from 0 to 50%,and the results are shown in Fig.2.Different colors represent different evaluations of self-healing on the same network.The results are considerably non-deterministic,and the extreme range of the results is more than 25%.As we can see from the Figures,in terms of both the number of links and the repair cost,the range of the evaluation results increases with a larger attack range.Since different evaluations of self-healing may get very different repair decisions,it is not convincing for practical applications.
2.3.Constraints of local information and short path length
Though only relying on local information is the superiority of self-healing,the absence of global information could influence the effectiveness of a repair significantly.As we can see in Fig.1,even in this very small network,self-healing could not guarantee its effectiveness.Without global information,each node may not recognize which nodes are more important to be linked.Therefore,only local information is not enough for a satisfying repair quality,and global information is necessary.
2.4.Redundancy of ineffective links
Since self-healing aims to repair a network for a larger GC-size at a low cost,it can be seen as a redundant link if the nodes of this link are already in the same component.This kind of links cannot increase the GC-size of the network.In other words,the resource of this link could be used in a more effective way.To show this deficiency of self-healing,it is used to repair two real-world networks(adjnoun and celegansneural,introduced in Section 4.1)to see the percentage of redundant links.
Fig.3 is the evaluation results of self-healing on two different networks,one containing 112 nodes and the other with 297 nodes(adjnoun and celegansneural).The charts both show the percentage of redundant links when the attack range varies from 0 to 50%.As the charts report,self-healing in both networks generates a high percent of redundant links.In the first network with 112 nodes,the percentage of redundant links can be up to 100%of the total added links and only two points are below 10%.From 0 to 25%of the attack,nearly all the per-centages of redundant links are more than 70%.Regarding the other network with 297 nodes,nearly 80%of the first 50%attacks have more than 60%redundant links.Though the redundancy may strengthen the connectivity of some connected components,this is not the goal of self-healing,which should be a larger GC-size at a low cost.
3.Greedy ranking repair strategy
Considering the limitation of self-healing discussed in Section 2,we attribute the unsatisfying results to the evaluation metrics used and the absence of global information.To simplify the problem,we want to modify the multi-objective optimization problem into a single-objective one.Therefore,in this section,we firstly concentrate on a new evaluation metric for network repair,and during the repair process,each node should get global information.Based on the new evaluation metric,a greedy ranking repair strategy and an improvement on the strategy are proposed.
3.1.Consideration on evaluation metrics
Firstly and naturally,one part,GC-size,is selected from the evaluation metrics of self-healing.When the evaluation metric is only GC-size,there is the optimal repair strategy,and the number of added links should be the number of components minus one.Links only need to be generated between components with the two largest GC-sizes after each repair of one link.For instance,Fig.4 shows the optimal repair process based on GC-size.In Fig.4(c),a series of components is sorted according to their sizes.If the network is supposed to be repaired for a larger GC-size,links only need to be generated between each component,and after adding only three links such as the orange dashed lines shown in Fig.4(d),the network would be fully connected.Even though the network is fully connected,the functionality of the network may not recover from damage.For example,in terms of the shortest path length of some node pairs which can represent the efficiency of the network,the shortest path length of nodemand nodeecould be at most 7 with the optimal GC-size repair strategy,while the network only has 11 nodes totally.Besides,there could be varieties of repair strategies to make the network fully connected,but the functionality of the network would be quite different when different links are generated,which also makes it confusing to determine the optimal repair strategy.
Secondly,we consider using the average shortest path length as the evaluation metric.However,as the traditional definition in the complex network theory,the shortest path length is only defined between two connected nodes.After some attempts on evaluation metrics,we come up with the total connectivity of the network to be the evaluation metric,which includes the influences of all the connections of node pairs in the network,no matter they are connected or disconnected.A connection of two connected nodes is defined to be the shortest path length,while a connection between two disconnected nodes to be a constant.Considering that the definition should correspond to the reality,this kind of connection should not be shorter than or equal to the diameter of the original network,because if so,transportation between these two nodes would be achieved by other ways instead of this network before attack.Thus,we set a connection of two nodes from different components to be:
where Diameter(Gorig)means the diameter of the original network.The new metric is
where Connection(n1,n2)means the connection betweenn1andn2.Though the formulation of the new metric is related to all the connections in the network,the new metric is indeed influenced by the GC-size of the network.Because a connection between two unconnected nodes is longer than the diameter of an original network,which should be much larger than the two nodes’SPL from one component of an attacked network,if there are two relatively large components in the network,the optimal repair link would be one between these two components to change many connections between components into connections within the same component.Since the new evaluation metric can also stand for the efficiency of a network,it conforms to realistic requirements.
In addition,we want to concern on the average shortest path length(ASPL)as well as the GC-size.Since the shortest path length is defined in a fully connected network,we can only use the average shortest path length of the giant component to represent that of the whole network.Because of different measurement units,the values of both the GC-size and the average shortest path length should be normalized.Therefore,we make a weighted sum of these two normalized values to be the evaluation metric as follows:
wherew1andw2are the weights of the GC-size and the ASPL,respectively.It is easy to normalize the GC-size since the value is already between 0 and 1,while the process of normalization for the ASPL is quite difficult.The maximum of the ASPL could not be determined easily.If the maximum is changed according to different topological structures,it is obviously unfair for different kinds of repair strategies,because for a network with a fixed number of nodes,the maximum should be the same.Finally,we set the value to be (n+1)/3,wherenis the number of nodes in the network.This value is calculated according to the worst situation in terms ofASPLfor a network ofnnodes,which is a line network,and the ASPL of a line network withnnodes is (n+1)/3.However,after some evaluations of this metric,we found that the ASPL influences so much on the weighted sum that the optimal repair strategy of this evaluation metric nearly repairs networks only for the smallest ASPL of the giant component,which would ignore the GC-size.
After the considerations on the evaluation metrics,we select the total connectivity to assess the quality of network repair.

Table 1 Algorithm 1:Greedy ranking algorithm.

Table 2 Algorithm 2:Speed-up greedy ranking algorithm(1st step).

Table 3 Algorithm 3:Speed-up greedy ranking algorithm(2nd step).

Table 4 Algorithm 4:Speed-up greedy ranking algorithm(3rd step).
3.2.Greedy ranking repair strategy based on total connectivity
After confirming our new evaluation metric,we consider to propose a new network repair strategy,which would behave well in terms of the new metric.The problem to be solved then is that when we want to generate a fixed number of links to an attacked network,which links should be generated to minimize the total connectivity of the network.However,obtaining the optimal solution to this problem is NP-hard.For a network containingnnodes,if we want to generatemlinks to make the total connectivity to be minimum,the computation complexity to get the optimal result isO(n2m+2).This value can be derived as follows:
For a network containingnnodes,there are totallynode pairs,wheremeans the number of combinations with 2 elements from totalnelements.Assuming the number of links in the network isl,there are (-l)links(the order of magnitude isn2),which can be generated for repair.Ifmlinks are expected,there would bedifferent combinations to be generated(the order of magnitude isn2m).For each combination,the total connectivity needs to be computed to check its effectiveness.Computing the total connectivity needs to consider all the node pairs in the network,so the order of magnitude to compute the total connectivity for one time isn2.Therefore,the computation complexity to get the optimal result isO(n2m+2).
We have tried to find the optimal result for a very small network(karate,introduced in Section 4.1)containing 34 nodes at a length of 4 optimal links,whose running time is already nearly 6 h.
Forced by the long running time,we propose a greedy ranking repair strategy to get a relatively optimal solution to the problem.In the greedy ranking repair strategy,we divide the problem ofmoptimal links intomseparated selections of one optimal link.Therefore,whenmlinks are supposed to be generated in a network,we firstly sort all the candidate links according to the metric values(total connectivity)of the network with the specific one candidate link.Then we add the optimal one link to the network,and refresh the candidate links.We redo the two preceding steps until we finally addmlinks to the network.The computation complexity of this greedy ranking repair strategy isO(n4).This value can be derived as follows:
For each optimal link,-lcandidate links need to be compared(the order of magnitude isn2).For each candidate link,the total connectivity of the network with the candidate link should be computed for one time,and the order of magnitude to compute the total connectivity for one time isn2.The order of magnitude to computemrelatively optimal links ism×n2.Since the repair cost could be limited,mis often much smaller thann.Therefore,the computation complexity of the greedy ranking repair strategy isO(n4).
In our repair strategy,we do not calculate all node pairs’connectivity because the software package used has an efficient method to get the ASPL of each component in the network.Thus,we calculate the total connectivity according to the following formulation:
where |Components(G)|means the number of components in network G,ASPL(i)means the ASPL of the ith component,|Components(i)|means the number of nodes in ith component,and Diameter(Gorig)is the diameter of the original network,which is used for a connection between two unconnected nodes in the network.In order to make the process of the greedy ranking repair strategy more clear,the pseudo code is presented in Table 1.In this paper,all shortest path lengths are computed with NetworkX 1.9.1,which is a Python library for studying graphs and networks.
3.3.Speed-up greedy ranking repair strategy
Though the greedy ranking repair strategy is much faster than the real optimal repair strategy,the computation complexity still needs to be optimized.The most natural idea to simplify the strategy is to avoid some tries on obviously ineffective links.Because the greedy ranking repair strategy needs to consider all node pairs in the network,we try to avoid some links,which can be easily identified as those not in the optimal repair links.In this speed-up strategy,we check the candidate links in order,and record the best one link and the total connectivity with this temporary best one link.When we check a new link,we estimate the upper-bound effectiveness of this new link to the whole network,and if this new link is better than the temporary best one,we compute the total connectivity of the network with this new link to check whether this new link is really better than that one.
The pseudo code of the speed-up strategy is shown as follows.The process of the strategy is divided into three parts:compute the total connectivity of a network,Table 2;select the best one link to be added,Table 3;select a fixed number of best links,Table 4.The improvement of the speed-up strategy comes from the second part.
Limited by the formulation of the effectiveness’upperbound estimation,the speed-up strategy can only avoid some redundant computations before the network is fully connected.Because all links need to be checked before its effectiveness is really evaluated,the running time would be a bit longer than that of the greedy ranking repair strategy after the network is fully connected.More improvement on the strategy in terms of computation complexity is our future work.
3.4.Effectiveness of greedy ranking repair strategy on a small example network
Because the speed-up strategy only avoids some links with poor effectiveness,the results of the greedy ranking repair strategy and the speed-up strategy are the same.Fig.5 shows the best three links with our repair strategy on the small attacked example network used in Section 2.The orange links are the added links.We can see that even though our evaluation metric is the total connectivity,the repair in this example network is also the optimal repair in terms of GC-size,which confirms that the new links between components are also important in terms of our metric.
4.Experimental evaluation
In this section,the optimality of self-healing and the effectiveness of the greedy ranking repair strategy are compared on six real-world networks and three kinds of random networks.The attack strategy during disruption is chosen according to degree,which means that nodes with a higher degree are attacked first.The relation between the total connectivity and the number of added links and that between the total connectivity and the cost of repair are discussed in this section.In addition to the effectiveness of each strategy,the running time of each strategy is also reported at the end of each type of networks.All experiments are conducted on a laptop with Intel(R)Core(TM)i7-4610M CPU@3.00 GHz processor and 4.00 GB main memory.All implementations of the network repair strategies are implemented in Python on Fedora 23.
4.1.Evaluation on real-world networks
Table 5 shows basic properties of the 6 real-world networks used in our study,and Fig.6 presents the visualizations of the 6 networks,where the size of a node is proportional to its degree.The graph layout in Fig.6 was created with the force-directed algorithm Fruchterman-Reingold.All networks are available for download at https://networkdata.ics.uci.edu/index.php.We can see from the Table 5 and Fig.6 that the structures of these 6 networks are quite diverse.
To evaluate the optimality of self-healing and the effectiveness of the greedy ranking strategy,we attack two different numbers of nodes in each of the 6 real-world networks and then repair them with both strategies.For self-healing,we change the parameters of self-healing and record all the results for 1000 executions,given that the outcome of self healing is non-deterministic.We vary parameterpfrom 0.1 to 0.9,and at the same time,varyrmaxfrom 2 to 5.For the greedy ranking repair strategy,we gradually increase the number of links to be added.The upper bound of the greedy strategy’s link number is fixed to the maximum of self-healing’s link number for the same network.Fig.7 reports the total connectivity as the number of added links changes.In Figs.7 and 8,the name means the to-be-repaired network and attack range,for instance,‘Adjnoun0.142” represents the adjnoun network with 14.2%nodes attacked.As we can see from Fig.7,in terms of the number of added links and the total connectivity,the greedy ranking repair strategy obtains much better results than those of self-healing.For all 12 scenarios of the 6 networks,the greedy ranking repair strategy’s total connectivity is less than that of self-healing.Nearly for all the networks,the greedy ranking repair strategy’s total connectivity decreases sharply in the first stage,and when the number of added links becomes similar to the high-parameter(p> 0.8,rmax> 4)self-healing results’link numbers,the slope of the total connectivity decreases.The large ranges of self-healing results also underline its strong non-deterministic behavior.It should be noted that in the football network,the results of self-healing and the greedy ranking repair strategy are very close,because the density of the football network is pretty high and even optimal results cannot decrease the total connectivity a lot.
Fig.8 shows the relation between the cost and the total connectivity of both self-healing and the greedy ranking repair strategy’s results.As we can see,though the goal of our network repair strategy is not related to the cost of repair,the greedy ranking repair strategy’s results are also better than those of self-healing in terms of cost,because more information is used.In terms of repair cost,self-healing’results are much more stable than those in terms of link number.
When it comes to running time,because the running time of the greedy ranking repair strategy is almost linear with the increase of the link number,the running time of only one added link with the greedy ranking repair strategy is shown.Table 6 reports all the running time of one link in all networks with the greedy ranking repair strategy and the running time of self-healing.Self-healing has a big advantage in terms of running time when compared with the greedy ranking repair strategy.
4.2.Evaluation on random networks:ER,BA,WS
In this part,the repair strategies are evaluated on three types of random networks(ER,BA,and WS).For each type of random network,we set the node number to be 100,and for each network,the attack ranges are 20%and 30%,respectively.The introduction of these three types of random networks is the following:

Table 5 Basic properties for the 6 networks used in our study.

Table 6 All running time for one link with the greedy ranking repair strategy and running time of self-healing.
(1)Erdos-Renyi(ER)network.In our experiment,we choose the G(n,p)model.In this model,the network consists of n nodes,which are connected randomly.Each edge is linked in the network with probability p independent from every other edge.Meanwhile,all networks with n nodes and m edges here have an equal probability,which is
In our evaluation,we setpto be 5%,10%,and 15%,respectively.
(2)Barabasi-Albert(BA)network.A BA network,whose degree distribution follows a power law,is absolutely different from an ER network.In this network model,there are also 2 parameters:n(number of nodes)and m(number of edges generated by one new node).The newly added node has a linear preferential as
wherekimeans the degree of nodei.In our evaluation,parametermis 2,3,and 4,respectively.
(3)Watts-Strogatz(WS)network.In a WS network model,there are 3 parameters:n(number of nodes),m(initial number of each node’s neighbors),and p(probability of each node rewiring).We set m to be 2 and p to be 10%,20%,and 30%in our evaluation.
Similar to the evaluation on real-world networks,Fig.9 shows the total connectivity as the link number differs.In Figs.9 and 10,the name means the to-be-repaired network,the parameter setting in the model and attack range,for instance, ‘ER(5)0.2” represents the ER network with 20%nodes attacked,when each edge is linked with a probability of 5%.Under all conditions of random networks,the greedy ranking repair strategy’s results are better than those of selfhealing.We can see that for ER networks,when the parameter setting is 10 or 15,which means each edge is linked with aprobability of 10%or 15%in the network,the trends of the two strategies’results are similar to that of the football network,because these two parameter settings make the networks’densities so high that even the optimal repair could not decrease the total connectivity a lot.For WS networks,because the attacked networks have many components and the connections between components are pretty long(nearly all the candidate links’distances are longer than the thresholdrmax),self-healing can hardly decrease the total connectivity.This point also highlights that only local information cannot repair networks effectively.

Table 7 All running time for one link with the greedy ranking repair strategy and running time of self-healing.
Fig.10 reports the total connectivity as the cost changes.The greedy ranking repair strategy behaves better even in terms of cost,which is similar to the results of real-world networks.As shown in the WS networks,because of the constraints of self-healing,even with large parameters,it cannot decrease the total connectivity a lot.
The running time of random networks is shown in a way similar to that of real-world networks.Since the running time of the greedy ranking strategy in random networks is still linear to the number of links,the running time of only one link with our strategy for each network is shown in Table 7.Because the WS networks have more components,the speedup strategy is more effective in these networks in terms of running time.
5.Conclusions and future work
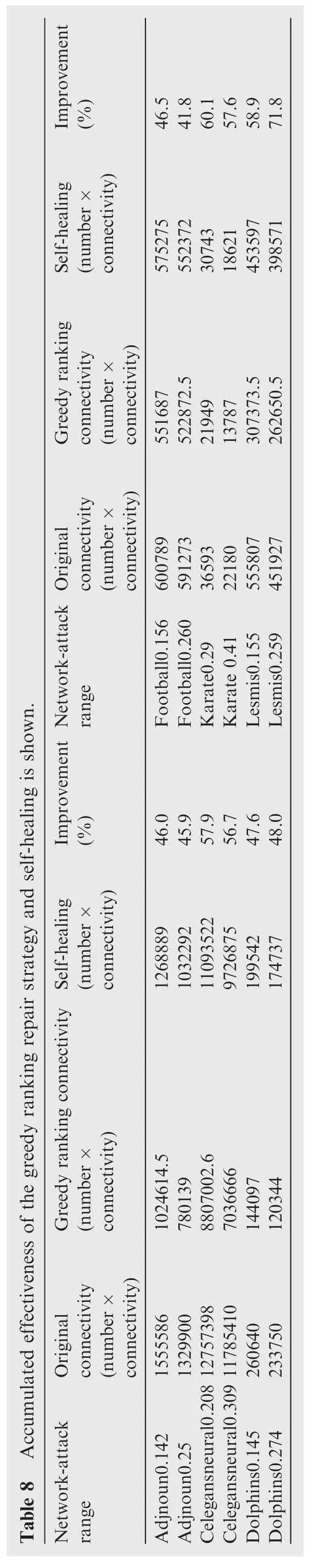
In this paper,we discuss a recently proposed network repair strategy self-healing and its optimality.Motivated by the limitation of this strategy,a new metric is devised to evaluate the network repair process,and according to this metric,a greedy ranking repair strategy and an improvement on the strategy are designed.The optimality of self-healing and the effectiveness of our strategy are evaluated on six real-world networks and three types of random networks with different parameters.Our results show that self-healing can be significantly improved by exploiting global information.This leads towards an interesting sweep point for research between locally and globally optimal repair.Table 8 reports the effectiveness of self healing for real-world networks.The value we choose to compare in this table is the area between the trend line of the connectivity value and thex-axis,which is the accumulated effectiveness of the strategy.As the table shows,the results are recorded as original connectivity,greedy ranking connectivity,and self-healing connectivity.Each value represents the area between the trend line of the connectivity points and thex-axis,while the connectivity points of self-healing are the average values of 1000-time executions.The ranges of all these three kinds of area on thex-axis are the maximums of the self-healing link numbers.Therefore,the unit of these values is ‘number× connectivity”.The red digits represent improvement,defined as follows:
The value of Improvement(%)should be between 0 and 100%.When Improvement(%)is close to 100%,it means that self-healing repairs the network ineffectively;when Improvement(%)is close to 0%,it means that self-healing’s result is nearly optimal.It is shown that all values of the improvement are more than 40%in the 12 networks;6 of them are more than 50%;2 of them are more than 60%.The results show that self-healing’s optimality can be improved significantly,by possibly exploiting non-local information.In conclusion,this paper leads to an effective evaluation metric on network repair,and sheds light on optimality of network repair strategies.
Air transportation networks are often vulnerable against emergencies or extreme weather,which are impractical to escape from.Therefore,an effective and efficient repair strategy is significantly important for transportation networks to restore their functions.This paper develops an evaluation metric to assess the functionality of networks and presents a greedy ranking strategy to help networks heal from damages.
Our work can be improved in the following aspects:
(1)Our current greedy ranking repair strategy checks all the candidate links,but only one link would be selected once,so there is no need to try each candidate link.Though the speed-up ranking strategy can avoid some ineffective links,but the speed-up process is only effective before the network is fully connected.Therefore,we have two choices to avoid more links:(A)make a more accurate estimation formulation,because current estimation formulation is very natural to come up with;(B)develop another technique for recognizing ineffective candidate links after the network is fully connected.
(2)Simplify the criterion when evaluating each candidate link.For current strategy,the criterion is to calculate the total connectivity after adding the candidate links.Since most of current running time is spent on this process,if we want to improve the running time of our strategy,the criterion must be simplified.Therefore,we will try to find a new criterion with similar effectiveness of the total connectivity,but with significantly reduced computation complexity.
Acknowledgements
This study was supported by the Research Fund from the National Natural Science Foundation of China (Nos.61521091,61650110516,and 61601013).
1.Parsons S,Atkinson PM,Simperl E,Weal M.Thematically analysing social network content during disasters through the lens of the disaster management lifecycle.The 24th international conference on world wide web companion,international world wide web conferences steering committee;2015 May 18–22;Florence.New York:ACM;2015.p.1221–6.
2.Ofei-Dodoo S,Medvene LJ,Nilsen KM,Smith RA,Dilollo A.Exploring the potential of computers to enrich home and community-based services clients’social networks.Educ Gerontol2015;41(3):216–25.
3.Padilha-Feltrin A,Quijano Rodezno DA,Mantovani JRS.Voltvar multiobjective optimization to peak-load relief and energy efficiency in distribution networks.IEEE Trans Power Delivery2015;30(2):618–26.
4.Havlin S,Kenett DY.Cascading failures in interdependent economic networks.In:Takayasu H,Ito N,Noda I,Takayasu M,editors.The international conference on social modeling and simulation,plus econophysics colloquium 2014;2015.p.87–97.
5.Guan X,Zhang X,Han D,Zhu Y,Lv J,Su J.A strategic flight conflict avoidance approach based on a memetic algorithm.Chin J Aeronaut2014;27(1):93–101.
6.Li S,Xu X.Vulnerability analysis for airport networks based on fuzzy soft sets:From the structural and functional perspective.Chin J Aeronaut2015;28(3):780–8.
7.Wandelt S,Sun XQ.Evolution of the international air transportation country network from 2002 to 2013.Transportation Res Part E2015;82(1):55–78.
8.Gallos LK,Makse HA.Scaling theory of transport in complex biological networks.Proc Natl Acad Sci U S A2007;104(19):7746–51.
9.Talikka M,Boue S,Schlage WK.Causal biological network database:a comprehensive platform of causal biological network models focused on the pulmonary and vascular systems.In:Hoeng MC,Peitsch MC,editors.Computational systems toxicology.New York:Springer;2015.p.65–93.
10.Gan C,Yang X,Liu W,Zhu Q,Jin J,He L.Propagation of computer virus both across the internet and external computers:A complex-network approach.Commun Nonlinear Sci Numer Simul2014;19(8):2785–92.
11.Liu N,An H,Gao X,Li H,Hao X.Breaking news dissemination in the media via propagation behavior based on complex network theory.Phys A:Stat Mech Appl2016;453:44–54.
12.Dong G,Du R,Hao H,Tian L.Modif i ed localized attack on complex network.EPL2016;11(2):28002.
13.Nie T,Guo Z,Zhao K,Lu ZM.The dynamic correlation between degree and betweenness of complex network under attack.Phys A:Stat Mech Appl2016;457:129–37.
14.Sun SW,Ma YL,Li RQ,Wang L,Xia CY.Tabu search enhances network robustness under targeted attacks.Phys A:Stat Mech Appl2016;446:82–91.
15.Alenazi MJ,Sterbenz JP.Evaluation and comparison of several graph robustness metrics to improve network.2015 7th international workshoponreliablenetworks designandmodeling(RNDM),2015 Oct 5-7;Munich.Piscataway(NJ):IEEE Press;2015.p.7–13.
16.Kinney R,Crucitti P,Albert R,Latora V.Modeling cascading failures in the North American power grid.Phys Condensed Matter2015;46(1):101–7.
17.Simonsen I,Buzna L,Peters K,Bornholdt S,Helbing D.Transient dynamics increasing network vulnerability to cascading failures.Phys Rev Lett2008;100(21):2539–41.
18.Zhou J,Huang N,Sun X,Wang K.A new model of network cascading failures with dependent nodes.Reliability maintainability symposium(RAMS);2015.p.1–6.
19.Wandelt S,Sun XQ,Cao XB.Computationally efficient attack design for robustness analysis of air transportation networks.Transportmetrica A:Transport Sci2015;11(10):939–66.
20.Wang J,Qiao C,Yu H.On progressive network recovery after a major disruption.Proc-IEEE INFOCOM2011;8(1):1925–33.
21.Liu X,Yuan Y.A novel dynamic method in distributed network attack-defense game.Math Probl Eng2015;2015:1–7.
22.Gallos LK,Fefferman NH.Simple and efficient self-healing strategy for damaged complex networks.Phys Rev E2015;92(5–1):052806.
14 July 2016;revised 20 October 2016;accepted 30 December 2016
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Review on signal-by-wire and power-by-wire actuation for more electric aircraft
- Real-time solution of nonlinear potential flow equations for lifting rotors
- Suggestion for aircraft flying qualities requirements of a short-range air combat mission
- A high-order model of rotating stall in axial compressors with inlet distortion
- Experimental and numerical study of tip injection in a subsonic axial flow compressor
- Dynamic behavior of aero-engine rotor with fusing design suffering blade of f
