银行间市场风险传染与网络结构演化研究

徐 涛，何 建 敏，李 守 伟

(东南大学 经济管理学院，江苏 南京 211189)

银行间市场风险传染与网络结构演化研究

徐 涛，何 建 敏，李 守 伟

(东南大学 经济管理学院，江苏 南京 211189)

文章构建了银行间市场动态网络结构模型和银行间市场多渠道风险传染模型，分析了风险传染环境下银行间市场网络结构演化特征以及流动性效应和挤兑效应对银行间市场网络结构的影响。仿真结果表明：构建的银行间市场网络既是无标度网络又是小世界网络；在网络演化过程中，网络的拓扑特征保持稳定；流动性效应和挤兑效应的增强对网络拓扑特征的影响较小，但增加了银行间市场网络的不稳定性。

银行间市场；网络结构；风险传染；动态演化

一、引 言

银行间市场是现代金融系统的重要组成部分。银行间通过借贷、支付清算、贴现、承兑、担保等形式形成了错综复杂的债权债务关联。一方面，流动性盈余的银行通过银行间市场为流动性短缺的银行提供流动性资金，对银行间市场的繁荣发挥积极作用[1-2]；另一方面，银行间的债权债务关联也使得银行系统面临潜在的风险，当银行出现失败时，银行间复杂的债权债务关联为风险传染提供了潜在的渠道[3-4]。当一家银行受到冲击而失败后，有可能无法满足其债权银行的清偿要求导致债权银行失败，并可能产生多米诺骨牌效应，对银行系统造成重大破坏。鉴于此，有必要对银行间市场的风险传染机制进行分析。风险传染是造成银行系统不稳定的重要因素，银行间市场风险可以通过不同渠道在银行间进行传染，甚至是多种渠道同时进行传染，但目前对银行间市场风险传染的研究主要集中于以下4种渠道[5]：(1)银行间的双边资产暴露；(2)共同冲击；(3)流动性渠道；(4)信息传染。

Allen和Gale[6]的研究结果表明银行间市场风险传染是一种均衡现象。基于网络理论，Aleksiejuk和Holyst[7]构建了二维有向网格的银行网络模型，研究发现：在该银行系统中，大多数银行失败时产生的传染效应很小；然而，该系统中还存在少数几个银行，它们失败时产生的传染效应很大。Thurner等[8]首次将动态博弈模型和银行网络拓扑结构相结合研究银行间市场规律，提出的动态分析模型中假设银行是自私的，银行之间没有合作行为。Iori等[9]分析了银行间市场随机网络中银行分为同质和异质情况下银行系统性风险的特征。Nier等[5]同样基于随机网络研究了银行间市场中违约引起的系统性风险。Lenzu和Tedeschi[10]通过银行彼此间的表现信任程度构建银行间的信贷联系，并发现随机网络较无标度网络在面对流动性冲击时具有更好的稳定性。Tabak等[11]研究发现巴西银行市场系统性风险是有限的。Souza等[12]发现巴西银行间市场的风险传染路径长度很短，巴西银行间市场风险传染是由中等规模的银行触发的。但是，Upper和Worms[13]揭示德国银行间市场存在货币中心结构；德国银行间市场分为上下两层结构，下层结构中的银行很少与其他类型的银行发生关联，而上层银行间较下层银行联系更紧密，更接近完全市场；另外，研究发现德国银行系统中潜在的传染风险是非常高的。同样地，Lelyveld和Liedorp[14]对荷兰银行进行了模拟冲击，发现银行系统的总资产损失率高达75%。马君潞等[15]在不考虑金融安全网的前提下，对我国银行间市场进行实证研究，发现只有中国银行和中国建设银行的倒闭冲击具有传染效应，而且在极端情况下中国银行的倒闭可能导致整个银行体系的崩溃。

流动性风险是银行间市场的内生现象[16]。Allen和Gale[17]指出当银行间拆借出现风险和银行面临挤兑时，单个银行的流动性风险可以传递给整个银行系统，即使银行间没有拆借和挤兑风险，单个银行的流动性风险也可以搅乱资本市场并进行传染。Cifuentes和Shin[18]指出更为严重的是，若银行的资产按照市场价格计算时，资产价格下跌会导致更多的银行出售资产，进而导致银行流动性风险在整个银行系统中传染，最终引发银行系统性风险。Nier等[5]对银行间市场风险传染过程中市场流动性变化进行建模，研究发现：市场流动性降低使得任何结构的网络变得更加脆弱。

信息溢出是银行间市场风险传染的一种重要渠道，冲击可以通过信息溢出在银行间市场进行传染[5]。通过信息溢出渠道的银行间市场风险传染表现在信息不对称形成的银行储户的挤兑行为。银行破产产生的信息溢出效应会增加未破产银行的再融资成本，银行为了保证流动性充裕，不得不减价销售自身资产，特别是在金融市场发生危机并存在羊群效应时，银行间市场产生流动性恐慌，使得银行大幅度地减价出售资产换取流动性。Chakrabarty和Zhang[19]发现信息溢出渠道的风险传染主要由直接的银行间资产负债关联引起的。Chakravarty等[20]改进了Diamond-Dybvig的模型，发现单个银行储户的挤兑行为会造成其他银行储户的恐慌，引起其他银行储户发生挤兑行为。He和Manela[21]系统地分析了银行间市场谣言传播时储户挤兑行为对银行运营的影响，发现危机时流动性不足的银行发生的挤兑行为可以缩短银行的幸存时间。郝明清和刘乐[22]基于向量自回归风险价值组合模型，分析了银行业与房地产业投资者情绪与风险传染问题，发现风险从房地产业向银行业的传染作用大于银行向房地产的传染。

现有对银行间市场网络结构特征的研究主要是对银行间市场的拓扑特性的实证分析。首先，银行间市场网络结构的实证研究发现其具有小世界和无标度特征。例如，Boss等[23]发现了奥地利银行间市场网络度服从双幂律分布，该网络具有小世界性质、分层结构和聚群结构特征。Souma等[24]对日本经济系统的网络结构特点进行了研究，发现日本银行网络具有无标度特征，且度的分布呈现出两段幂律。Kanno[25]对日本银行间市场实证分析，该银行网络节点包含银行和金融公司两种类型，发现日本银行网络具有无标度特征，且度的分布呈现出两段幂律。Soramaki等[26]在研究美联储电子转移支付系统中银行间债务联系时，发现美国的银行间网络具有小世界网络特征。其次，多国银行间市场网络结构的实证分析还表明银行间市场网络具有分层结构和货币中心结构。例如，Craig和Peter[27]通过德国中央银行1999～2012年间银行双边暴露数据，分析得到德国银行系统存在很强的分层特征。然后，学者们还发现多国的银行间市场网络中存在群聚结构。Iori等[28]研究还发现意大利银行间市场网络中具有两个群聚结构。Cajueiro和Tabak[29]基于复杂网络方法研究巴西银行间市场网络结构特征，发现巴西银行间市场网络也具有群体结构，另外其还具有高度的异质性。此外，银行间市场网络是动态演化的。Iori等[30]对意大利银行间市场进行研究，研究发现：从1999年到2002年间意大利银行间市场结构随时间的推移逐年在演化；意大利银行间市场网络结构是随机网络，该网络中主体间资金借贷的偏好性有限，且大银行可能从许多小银行处拆借资金。Martinez-Jaramill等[31]通过研究墨西哥银行间资金网络，发现随着时间的改变，银行间的债务联系大部分是稳定的，而少数的、局部的联系会发生变化。

已有关于银行间市场网络结构与风险传染关系的研究主要分析网络结构对网络稳定性的影响。A11en和Gale[6]基于不同的银行间市场结构假设，研究了银行间市场中的风险传染问题。Allen和Gale研究的结果表明，银行间市场风险传染是一种均衡现象，揭示了金融风险传染与金融债权的内生模式有重要的关系：与非完全市场结构相比，完全市场结构更易于化解银行系统面临流动性冲击时带来的系统风险。Aleksiejuk等[32]基于不同的银行网络结构模型，揭示了银行风险传染过程中存在的自组织临界现象。Nier等[5]研究发现银行随机网络集中度对传染风险的影响不是单调的，最初集中度表现在一小部分传染效应的增加，但是在集中度超过一个阈值之后却提高了银行系统吸收冲击的能力。Krause和Giansante[4]模拟了不同标度参数的银行间网络，他们的研究认为银行间网络标度参数越小、集中度越高，发生违约传染的可能性越小。Ladley[33]通过内生的银行行为模型揭示：不存在一种银行间市场网络结构对所有条件的冲击均呈最优状态；当面对大范围冲击时，稠密的网络结构较稀疏的网络结构更容易遭受冲击破坏。隋聪等[34]发现集中度越高的网络由于传染而倒闭的银行数量越多；但是，当基础违约的银行数量不多时，网络集中度越高，由于传染而倒闭的银行的总资产越少。

综合上述分析，现有银行间市场风险传染与网络结构的研究包括：银行间市场单渠道风险传染机制分析、银行间市场网络结构拓扑特征分析和网络结构与银行间市场网络稳定性的关系分析。但在实际银行间市场中，不同形式的风险可以通过多种渠道同时传染，而且传染风险通过多种渠道相互影响、相互促进。因此，现有银行间市场风险传染模型尚存不足，现有文献未构建多渠道银行间市场风险传染模型。另外，现有针对网络结构与风险传染二者关系的研究，主要集中于分析不同的网络结构对风险传染的影响，但未对风险传染如何影响银行间市场网络结构这一问题展开研究。解决上述问题和不足是本文的研究目的。

二 、网络结构模型

为了形式化地描述银行间市场模型，采用有向图G=(V,E)表示银行间市场网络，其中，顶点集V表示所有银行节点组成的集合，有向边集E是银行间拆借关联构成的集合。如果银行节点i,j∈V，则存在有向边ei,j，当且仅当银行i与银行j存在拆借关联，其中，银行i为债权银行，银行j为债务银行。假定银行总数|V|=N，Ni表示银行i所有邻居组成的集合(如果存在i到j的有向边，则j是i的邻居)。矩阵X=(xij)N×N表示银行间信用拆借规模，xij表示银行i向银行j的拆借规模。银行初始资产负债表、银行间市场网络的构建、更新及多渠道风险传染过程如下。

1.银行初始资产负债表的构建

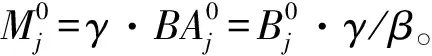
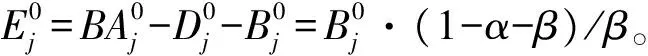
2.银行资产负债表的更新

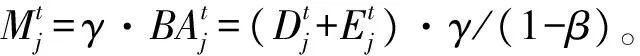
3.银行间市场网络的构建

银行间市场网络的构建过程主要基于下面两个假设：(1)拆借规模差别较大的银行间较拆借规模相近的银行间更容易建立拆借关联[35]；(2)银行间市场的网络结构是动态演化的[30]，并且银行间市场网络结构的构建仅与最新的银行拆借规模有关，与之前的拆借关联无关。

假设(1)的解释是：拆借规模较小的银行一般而言资产规模也相对较小，吸收风险能力较差，因此，更偏好将资金贷给规模较大的银行，这样可以降低拆借风险；而拆借规模较大银行一般总资产规模也较大，抵抗风险冲击能力强，在银行间市场中贷出资金时，优先考虑同业拆借利率报价，小银行由于自身规模小，往往给出更高的报价，因此，大银行偏好将资金分散地贷给不同的小银行，这样既能将风险尽可能地分散化又能获得较高的收益。假设(2)的解释是：银行间的拆借行为一般期限较短，只能作为流动性盈亏银行的短缺拆借，不能作为长期投融资方式，因此，银行间市场网络结构与银行间的拆借行为同步演化。基于上述分析，银行间市场网络结构具体构建过程如下：

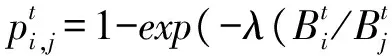
4.冲击与风险传染机制

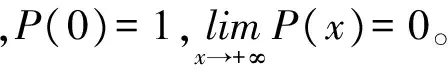
形式化地，如果sj>Ej，那么银行j失败，并且银行j的外部资产需要出售变现。如果sj-Ej≤Bj，那么sj全部被银行j的债权银行吸收。否则，银行j的储户存款吸收剩余损失。银行j的非债权银行k因市场中的流动性下降，银行k资产价格下降而受到冲击sk=Ik(1-exp(-φIj))；债权银行i不仅受到资产价格下跌的冲击，还要吸收银行j的残余损失，因此，受到的总损失si=xij(s-Ej)/Bj+Ij(1-exp(-φIj))。如果s≤Et,t≠j，银行t经受住冲击而幸存下来；否则银行t失败，并可能触发下一轮传染。这个过程一直进行下去，直至损失被全部吸收或所有银行都失败。

三、仿真分析

假定仿真模型中银行节点总数N=200，幂律分布参数τ=1.8[23]，根据《2014中国金融统计年鉴》数据，设定储户初始存款占银行初始总资产的比例α=0.8，银行间借款占银行总资产的比例β=0.1，流动性资产占银行总资产的比例γ=0.05，另外，依据我国商业银行存贷款基准利率表，设定y1=6%,y2=5%,rb=4%,rd=2%。由于σ1,σ2和风险偏好参数γ未见相关文献给出相关基准值，因此，对其基准值作如下假定：σ1=0.05,σ2=1,γ=0.01,φ=0.0003。

1.风险传染对网络结构演化的影响

(1)累积度分布的演化

从图1中可以看出，对于初始银行间市场网络，出入度累积概率分布在双对数坐标轴下趋于直线，因此，出入度累积概率分布均服从幂律分布，仿真网络为无标度网络，且出度和入度的累积概率分布无显著差异。这是由于少数大银行的信用拆借关联很多，与其他银行的信用拆借业务多，而小银行的信用拆借关联少，与其他银行的信用拆借业务也较少。构建的银行间市场网络结构与现有实证结构相符，奥地利和日本银行间市场网络的度分布服从双幂律分布[23-24]，Inaoka等[36]分析银行、证券公司和其他金融机构形成的金融市场网络结构一致，累积度均服从幂律分布。随着仿真期数t的增加，累积度概率分布也进行演化，但是出入度累积概率分布依然服从幂律分布。这表明银行间市场网络结构是一个动态稳定的网络。这一结论与Jaramillo等[31]对墨西哥银行间市场网络结构的动态演化结论吻合。

(2)网络聚集系数的演化

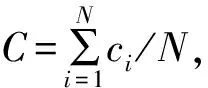
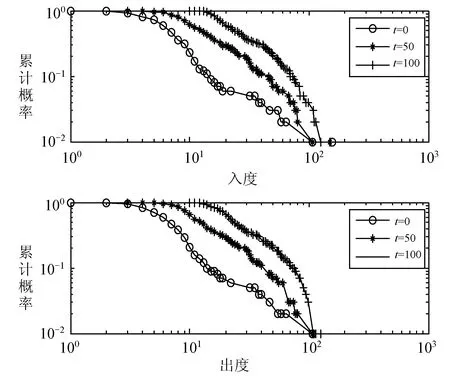
图1 累积度的概率演化图

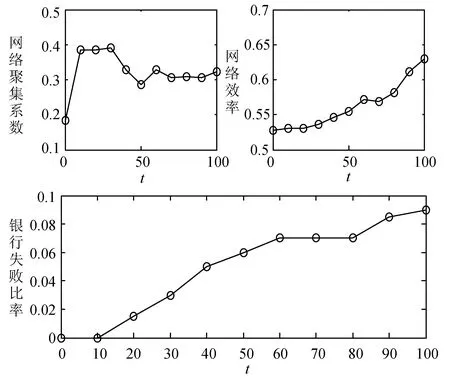
图2 网络聚集系数、网络效率与银行失败比率的演化图

从图2(上左)可以看出，网络聚集系数随时间t非线性演化。当0≤t<10时，银行间市场网络的聚集系数随时间的推移迅速增大；当10≤t<30时，网络聚集系数随时间t的增大保持动态稳定；当30≤t<50时，网络聚集系数随时间t的增大而减小；当50≤t≤100时，网络聚集系数随时间t的增长保持动态稳定。总体而言，随时间t的增长，网络聚集系数在区间(0.3,0.4)内小幅震荡，网络聚集系数保持动态稳定。这一结论与Jaramillo等[31]对墨西哥银行间市场网络结构的研究结论相符。

(3)网络效率的演化

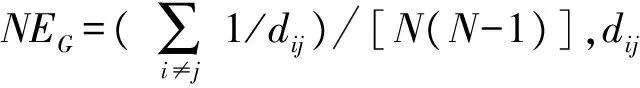
从图2(上右)中可以看出，随着时间t的增大，网络聚集系数也随之震荡增大，网络聚集系数的取值范围在(0.5,0.65)。通过网络效率的计算公式可知，构建的银行间市场网络是小世界网络，这一结论与墨西哥和美国的银行间市场网络结构的实证分析结果一致[25,30]。

(4)风险传染

通过失败银行占所有银行的比率描述银行失败规模。图2(下)给出失败银行比率随时间t变化的曲线。从图2(下)可以看出，当0≤t<10时，失败银行占所有银行的比率为0，这表明此阶段没有银行失败；当10≤t<60时，随着时间的推移，失败银行的比率逐渐增加，这是因为在此阶段中，出现个别银行失败并将残余损失传递给其债权银行，而且其债权银行的权益不足以吸收残余损失，形成新一轮的银行失败；当60≤t<80时，失败银行的比率保持不变，这表明在此阶段没有银行失败，这是因为此时银行间市场网络中银行的权益足够吸收冲击；而当80≤t≤100时，失败银行的比率不断上升，这是由于在此阶段，新的一轮银行失败被触发，并产生传染效应。

2.外部冲击对网络结构及网络稳定性的影响

(1)流动性效应

银行失败造成市场中流动性减少，引发银行资产价格下跌，资产价格下跌会使得更多的银行出售资产，从而产生恶性循环，导致更多银行减价变现资产，对银行间市场网络的稳定性形成进一步冲击。图3给出了在期数t=100时，网络聚集系数、网络效率和失败银行占所有银行的比率与市场流动性效应的关系。

从图3可以发现，网络聚集系数随流动性效应参数φ的增大不断震荡，网络聚集系数的取值范围在(0.3,0.45)内；网络效率随流动性效应的参数φ的增加同样保持震荡，网络效率的取值在(0.55,0.65)内，通过网络效率的计算公式可知仿真网络为小世界网络。另外，还可以从图3发现，随着流动性效应参数φ的增大，失败银行的占比不断增加，这是因为流动性效应参数φ的增大，导致银行资产价格下跌的速度变快，使得银行间市场的稳定性受到更严重的冲击。从网络聚集系数和网络效率曲线的变化规律还可以得出，流动性效应的强弱对网络拓扑结构的影响较小，银行间市场网络保持动态稳定。

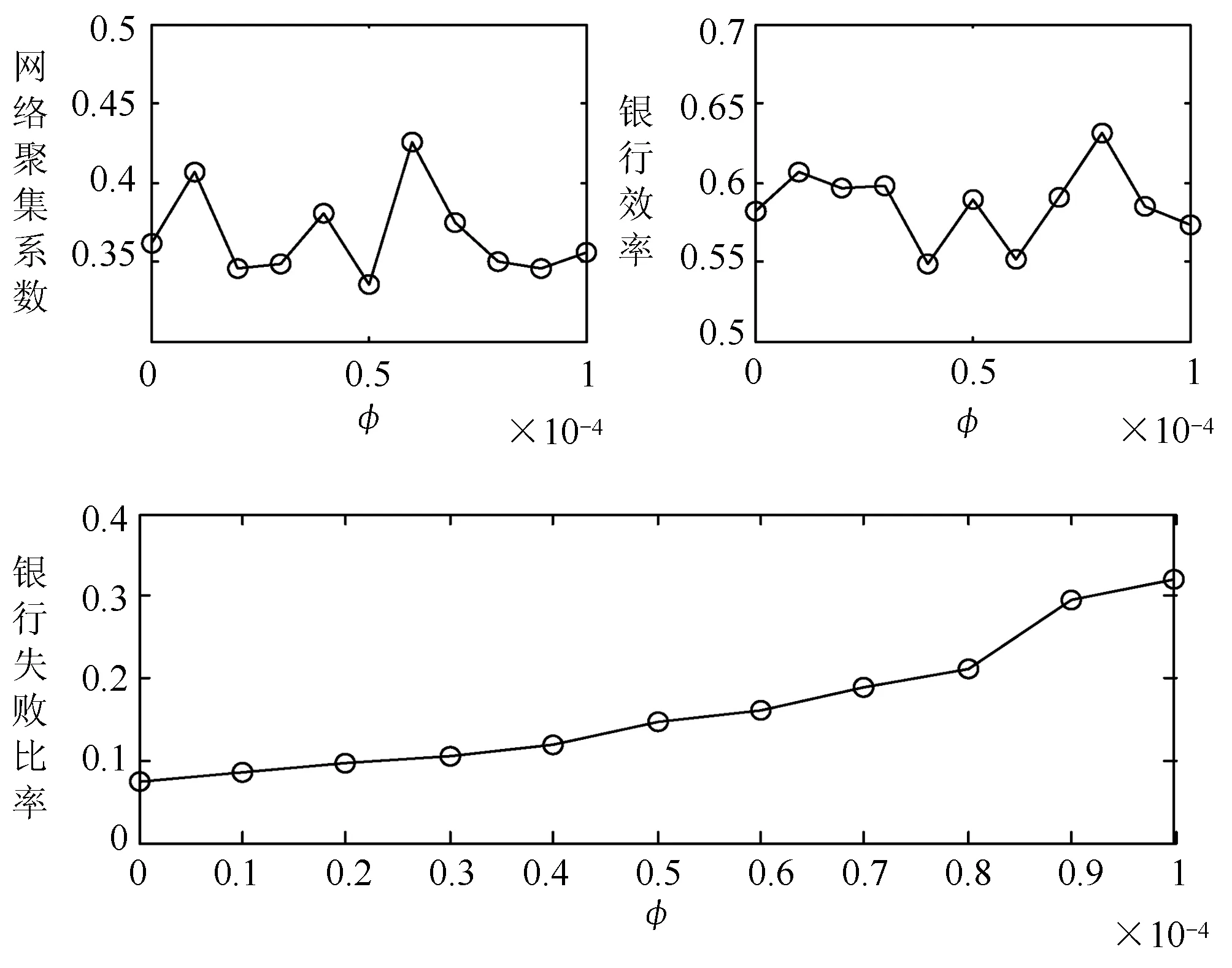
图3 网络聚集系数、网络效率和银行失败比率与流动性效应的关系图

图4 网络聚集系数、网络效率和银行失败比率与挤兑效应的关系图

(2)挤兑效应

储户的挤兑行为会造成银行资产负债表的剧烈变化，是造成银行失败的重要原因，并可能在银行间市场中产生传染效应，导致更多银行失败。通过储户存款波动标准差σ1描述储户的挤兑行为，图4给出了在期数t=100时，网络聚集系数、网络效率和失败银行比率与挤兑效应的关系图。从图4中可以看出，网络聚集系数与网络效率随σ1的不断增加保持震荡，网络拓扑特征动态稳定；由于网络效率的取值范围在(0.57,0.63)之间，可知银行间市场网络保持为小世界网络。另外，可以从图4中发现，随着挤兑效应的增大，银行网络中失败的银行的比率逐渐变大，这表明挤兑效应的增加可以增大银行间市场网络的不稳定性。

四、结 论

本文构建动态银行间市场网络结构模型和多渠道风险传染模型，通过构建的模型对银行间市场网络进行了演化仿真分析和外部冲击仿真分析。主要得到以下结论：构建的银行间市场网络结构具有小世界特征，即具有较短的平均最短路径长度和较高的聚集系数；另外，构建的银行间市场网络结构具有无标度特征，即少数银行具有较大的度，而大多数银行具有较小的度；此外，构建的银行间市场网络具有演化特征，演化过程中银行间市场网络结构保持动态稳定。银行间市场风险传染也会影响银行间市场网络结构拓扑特征。随着失败银行比率的增加，网络聚集系数和网络效率逐渐下降，这是因为失败银行比率的提升会引起银行间市场网络节点总数的减少，银行间可能的路径条数减少。外部冲击是造成银行失败的重要因素，但对构建银行间市场网络的影响较小。

研究结果对银行监管具有一定的实际指导意义。对于银行监管部门，需要保障市场中流动性平稳，尽量降低市场流动性，减少导致的银行资产价格下跌对银行系统稳定性的冲击；另外，要防止银行系统挤兑事件发生，一旦发生储户挤兑，监管部门需要安抚储户情绪，避免储户恐慌，防止发生连环挤兑事件。

[1] COCCO J F，GOMES F J，MARTINS N C.Lending relationships in the interbank market [J].Journal of Finance Intermediation，2009，18(1)：24-48.

[2] TEMIZSOY A，IORI G，MONTES-ROJAS G.The role of bank relationships in the interbank market[J].Journal of Economic Dynamics and Control，2015，(59)：118-141.

[3] GAI P，KAPADIA S.Contagion in financial networks [J].Proceedings of the Royal Society A：Mathematical，Physical and Engineering Science，2010，466(2120)：2401-2423.

[4] KRAUSE A，GIANSANTES.Interbank lending and the spread of bank failures：a network model of systemic risk[J].Journal of Economic Behavior & Organization，2012，83(3)：583-608.

[5] NIER E，YANG J，YORULMAZER T，etal.Network models and financial stability[J].Journal of Economic Dynamics and Control，2007，31(6)：2033-2060.

[6] ALLEN F，GALE D.Financial contagion[J].Journal of political economy，2000，108(1)：1-33.

[7] ALEKSIEJUK A，HOLYST J A.A simple model of bank bankruptcies[J].Physica A：Statistical Mechanics and its Applications，2001，299(1)：198-204.

[8] THURNER S，HANEL R，PICHLER S.Risk trading，network topology and banking regulation[J].Quantitative Finance，2003，3(4)：306-319.

[9] IORI G，JAFAREY S，PADILLA F G.Systemic risk on the interbank market [J].Journal of Economic Behavior & Organization，2006，61(4)：525-542.

[10] LENZU S，TEDESCHI G.Systemic risk on different interbank network topologies[J].Physica A：Statistical Mechanics and its Applications，2012，391(18)：4331-4341.

[11] TABAK B M，TAKAMI M，ROCHAJ M C，etal.Directed clustering coefficient as a measure of systemic risk in complex banking networks[J].Physica A：Statistical Mechanics and its Applications，2014，(394)：211-216.

[12] SOUZA S R S，TABAK B M，SILVA T C，etal.Insolvency and contagion in the Brazilian interbank market[J].Physica A：Statistical Mechanics and its Applications，2015，(431)：140-151.

[13] UPPER C，WORMS A.Estimating bilateral exposures in the German interbank market：is there a danger of contagion? [J].European Economic Review，2004，48(4)：827-849.

[14] LELYVELD I，LIEDORP F.Interbank contagion in the Dutch banking sector：a sensitivity analysis [J].International Journal of Central Banking，2006，2(2)：99-133.

[15] 马君潞，范小云，曹元涛.中国银行间市场双边传染的风险估测及其系统性特征分析[J].经济研究，2007，42(1)：68-78.

[16] HEIDER F，HOEROVA M，HOLTHAUSEN C.Liquidity hoarding and interbank market rates：the role of counterparty risk[J].Journal of Financial Economics，2015，118(2)：336-354.

[17] ALLEN F，GALE D.Financial fragility，liquidity，and asset prices [J].Journal of the European Economic Association，2004，2(6)：1015-1048.

[18] CIFUENTES R，SHIN H S，FERRUCCI G.Liquidity risk and contagion [J].Journal of the European Economic Association，2005，(3):556-566.

[19] CHAKRABARTY B，ZHANG G.Credit contagion channels：market microstructure evidence from Lehman Brothers’ bankruptcy[J].Financial Management，2012，41(2)：320-343.

[20] CHAKRAVARTY S，FONSECA M A，KAPLAN T R.An experiment on the causes of bank run contagions[J].European Economic Review，2014，(72)：39-51.

[21] HE Z，MANELA A.Information Acquisition in Rumor-Based Bank Runs[J].The Journal of Finance，2014，71(3)：1113-1158.

[22] 郝明清，刘乐.房地产业与银行业的投资者情绪与风险传染[J].大连理工大学学报(社会科学版)，2016，37(4)：91-97.

[23] BOSS M，ELSINGER H，SUMMER M，etal.Network topology of the interbank market [J].Quantitative Finance，2004，4(6)：677-684.

[24] SOUMA W，FUJIWARA Y，AOYAMA H.Complex networks and economics[J].Physica A：Statistical Mechanics and its Applications，2003，324(1)：396-401.

[25] Kanno M.The network structure and systemic risk in the Japanese interbank market[J].Japan and the World Economy，2015，(36)：102-112.

[26] SORAMKI K，BECH M L，ARNOLD J，etal.The topology of interbank payment flows[J].Physica A：Statistical Mechanics and its Applications，2007，379(1)：317-333.

[27] CRAIG B，VON PETER G.Interbank tiering and money center banks[J].Journal of Financial Intermediation，2014，23(3)：322-347.

[28] IORI G，RENO R，DE MASI G，etal.Trading strategies in the Italian interbank market[J].Physica A：Statistical Mechanics and its Applications，2007，(376)：467-479.

[29] CAJUEIRO D O，TABAK B M.The role of banks in the Brazilian interbank market：does bank type matter?[J].Physica A：Statistical Mechanics and its Applications，2008，387(27)：6825-6836.

[30] IORI G，DE MASI G，PRECUP O V，etal.A network analysis of the Italian overnight money market[J].Journal of Economic Dynamics and Control，2008，32(1)：259-278.

[32] ALEKSIEJUK A，HOLYST J A，KOSSINETS G.Self-organized criticality in a model of collective bank bankruptcies[J].International Journal of Modern Physics C，2002，13(3)：333-341.

[33] LADLEY D.Contagion and risk-sharing on the inter-bank market[J].Journal of Economic Dynamics and Control，2013，37(7)：1384-1400.

[34] 隋聪，迟国泰，王宗尧.网络结构与银行系统性风险[J].管理科学学报，2014，17(4)：57-70.

[35] TABAK B M，CAJUEIRO D O，SERRA T R.Topological properties of bank networks：the case of Brazil [J].International Journal of Modern Physics C，2009，20(8)：1121-1143.

[36] INAOKA H，TAKAYASU H，SHIMIZU T，etal.Self-similarity of banking network[J].Physica A：Statistical Mechanics and its Applications，2004，339(3)：621-634.

TheContagioninInterbankMarketRiskandtheEvolutionofNetworkStructure

XUTao,HEJianmin,LIShouwei

(SchoolofEconomics&Management,SoutheastUniversity,Nanjing211189,China)

This paper introduces a dynamic network and multi-channel contagion model for interbank market.The evolutionary features of interbank market network under contagion environment are analyzed and the effects of liquidity and run on the stability of interbank market network are investigated.Simulation results demonstrate that the constructed interbank market network has both scale-free and small-world features.In the evolution process of the network,the topology characteristics remain steady.The increasing liquidity and run effects have little impact on the topology features of the network,but could amplify the fragility of the network.

interbank market; network structure; risk contagion; dynamic evolution

10.19525/j.issn1008-407x.2017.04.008

F830.9

A

1008-407X(2017)04-0056-08

2016-10-12;

2016-12-09

国家自然科学基金资助项目：“基于复杂网络和Multi-Agent融合的金融市场间风险溢出效应研究”(71371051)

徐涛(1987-)，男，山东烟台人，东南大学经济管理学院博士研究生，主要从事金融工程研究，Email：xutaoseu@126.com；何建敏(1956-)，男，江苏无锡人，教授，博士生导师，主要从事金融工程研究；李守伟(1984-)，男，安徽蚌埠人，副教授，主要从事金融风险分析与管理研究。