基于六相参数信息的不换位同塔双回线距离保护研究
2017-11-16张世锋杨赟磊
张世锋,杨赟磊,常 潇
(国网山西省电力公司电力科学研究院,山西太原 030001)
基于六相参数信息的不换位同塔双回线距离保护研究
张世锋,杨赟磊,常 潇
(国网山西省电力公司电力科学研究院,山西太原 030001)
指出不换位同塔双回线发生故障时,保护的测量阻抗不仅受线间互感的影响,还要受到本回线各序分量相互耦合的作用,使得测量阻抗精度难以满足距离保护的要求。阐明了直接使用两回线电气量及六相阻抗矩阵对故障回路列写电压平衡方程,从而推导出适用于不换位同塔双回线各种故障类型下的距离保护算法。以理论分析和PSCAD数字仿真证明,该算法能承受线路较大的不对称性且耐过渡电阻能力高,具有良好的距离保护动作性能。
不换位同塔双回线;六相阻抗矩阵;过渡电阻;距离保护
理想换位同塔双回线发生故障时,保护的距离元件经邻线零序电流补偿后能较为准确地计算出保护安装处到故障点的阻抗值。但是在实际工程中对于短程输电线路或者高压尤其超高压线路,出于技术上和经济上的考虑,线路往往不换位或进行不完全换位。此时保护的测量阻抗不仅仅受邻线互感的影响,同时还感受到本回线各序分量之间的相互耦合作用,使得距离元件即使经邻线零序电流补偿后也会表现出一些复杂的特性,距离保护动作性能也可能不满足工程要求[1-3]。
本文首先定量研究了不换位同塔双回线距离保护经邻线零序电流补偿后测量阻抗的变化规律,指出其应用的局限性。然后基于线路故障回路直接使用两回线电气相分量及六相阻抗矩阵列写电压平衡方程,推导出了适用于不换位同塔双回线各种故障类型下的距离保护算法。
同塔双回线发生单相接地故障时,往往伴随着较大的过渡电阻,同样也存在保护范围的缩短和超越问题[4-5]。本文通过对不换位同塔双回线单相接地故障电气特征进行分析,然后推导了一种消除过渡电阻的方法。最后通过PSCAD/EMTDC软件对不同故障类型、故障位置以及过渡电阻情况进行了大量的数字仿真,验证了所提算法的有效性。
1 理想换位同塔双回线距离保护算法
1.1 理想换位同塔双回线单相接地故障
图1所示为理想换位同塔双回线其中一回线发生单相接地故障时的故障模型。
当I回线路发生单相接地故障时,保护安装处故障相母线电压要受到另一回线零序电流的耦合作用,其表达式如下。

式中,I1φ为保护安装处故障相电流;I10及I20分别为线路I和线路II的零序电流;K为本线零

图1 理想换位同塔双回线系统框图
序电流补偿系数,且K=(Z0-Z1)/3Z1。从式(1)可以看出,计算电流经相邻线路零序电流补偿后,即可精确地计算故障阻抗。
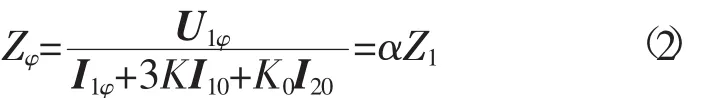
式中,K0=3Zm/Z1。
1.2 理想换位同塔双回线单回线相间故障
当理想换位同塔双回线在其中一回线发生相间故障如IAB时,保护安装处两故障相电压都要受到另一回线零序电流互感的作用,其表达式为

公式中UF表示故障点处的电压,此时相间测量阻抗为
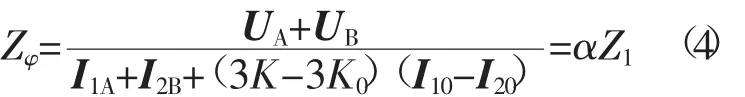
式(4) 也说明理想换位线路发生单回线相间故障时,距离保护的测量阻抗不受邻线零序电流互感的影响。同样当发生单回线相间接地故障时,经分析可知,式(4)也可以准确计算故障阻抗。
1.3 理想换位同塔双回线跨线故障
理想换位同塔双回线发生跨线故障如IA-IIB时,两回线的零序电流通过零序互感相互影响,此时保护安装处两故障相电压为

对于式(5),稍作整理即可得出测量阻抗的准确计算方法。
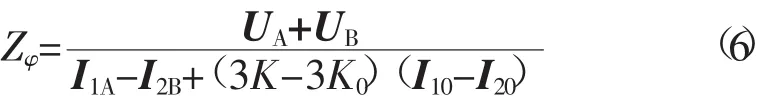
2 不换位同塔双回线距离保护算法推导
基于线路故障回路直接使用两回线电气相分量及六相阻抗矩阵列写电压平衡方程,推导适用于不换位同塔双回线各种故障类型下的距离保护算法。首先给出不换位同塔双回线单相接地故障的系统结构框图,如图2所示。

图2 不换位同塔双回线系统框图
基于既定的钢塔结构和相序布置方式,不换位同塔双回线对应的六相阻抗矩阵M表示如下。

矩阵M对称,其中对角线元素表示六相线路各相自阻抗;左上角和右下角18个元素指代线路I各相与线路II各相之间的互阻抗;剩余的其他元素表示线路I相间互阻抗和线路II相间互阻抗。
2.1 不换位同塔双回线单相接地故障
不换位同塔双回线发生单相接地故障如IAG时,故障相电压要受到其他相别的电磁耦合作用。为简化表达,可以忽略线路II正序和负序电流对线路I的互感作用,只计及两回线间的零序互感及线路I的不对称性,此时保护安装处故障相感受到的电压为

此处,Zm依然表示两回线间零序互感,其值近似用阻抗矩阵M中右上角9个线间互阻抗的平均值来表示。这样就可以较为准确地得出不换位同塔双回线单相接地故障时测量阻抗的表达式,如式(8) 所示。在构成距离保护时,取线路全长故障相自阻抗的80%作为距离I段的保护定值。

2.2 不换位同塔双回线单回线相间不接地故障
当不换位同塔双回线发生单回线相间不接地故障时,同样根据六相间的电磁耦合关系可以列出保护安装处测量电压的表达式,例如发生IAB故障时,如式(9)。

此处近似认为故障两相电流大小相等,方向相反。对式(9)两电压方程作差后稍作整理有
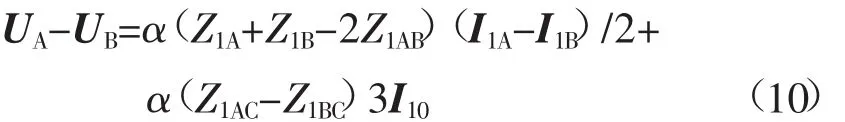
线路发生相间不接地故障时,线路网络没有零序源,只有很小的因线路参数不对称带来的零序电流,故等式右端第2项可以忽略,此时测量阻抗为

因此对于不换位同塔双回线单回线相间不接地故障,可以采用式(11) 相对准确地计算故障阻抗,不过需用L(Z1A+Z1B-2Z1AB)/2作为保护距离I段的定值,这里的L是同塔双回线路的长度。
2.3 不换位同塔双回线单回线相间接地故障
当不换位同塔双回线发生单回线相间接地故障时,理论上可以按文献 [6]所提的方法,根据三相线间环路列写电压平衡方程准确求解处保护安装处至故障点的距离,并以此构成距离保护。但该方法计算过程繁杂且需求取一元二次方程,对微机计算速度和存储空间有更高的要求,对构成距离保护来说不很理想。
可以看出,当线路趋于对称时,单回线相间接地故障测量阻抗的值也趋近于式(11)的计算结果。虽然通过理论推导并不能得出式(11)所示的等式,但只要式(11)的计算结果与等式右侧的数值之差在一个合理的范围之内,就依然可以构成距离保护,本文后续的仿真就说明了这一点。
因此对于不换位同塔双回线单回线相间接地故障,依然沿用式(11)来计算故障阻抗,并同样使用L(Z1A+Z1B-2Z1AB)/2作为保护距离一段的定值。
2.4 不换位同塔双回线跨线故障
对于不换位同塔双回线跨线故障,同样也可以利用文献 [6]所提的方法来准确求取故障距离,进而做成距离保护。但该过程同样比较复杂,没有较为统一的阻抗计算形式。
通过研究发现,线路不换位时,使用式(6)计算得到的测量阻抗误差相对较小,可以满足距离保护动作性能的要求。在计算过程中,定义不换位线路的正序阻抗Z1和零序阻抗Z0,如式(12)所示。其中,ZL表示双回线六相自阻抗的平均值,ZS表示线路I和线路II的6个相间互阻抗的平均值。

故对于不换位同塔双回线跨线故障,沿用式(6) 来计算故障阻抗,并取线路全长正序阻抗的80%作为距离I段的定值,此处正序阻抗由式(12) 计算得到。
2.5 不换位同塔双回线单相经过渡电阻接地故障
同塔双回线发生单相接地故障时,往往伴随着较大的过渡电阻,同样也存在保护范围缩短和超越的问题,因此有必要对消除单相接地过渡电阻的距离保护算法进行研究。
以图2为蓝本,当线路IA相发生经过渡电阻RK的单相接地故障时,根据文献 [6]所提方法可以计算得到对端变电站故障相的电流为

其中

此时,故障点电流IK便为已知,如式(14)所示。

于是保护安装处故障相感受到的电压UK表示成如下形式。

对故障相电流进行补偿,即

那么测量阻抗除所求的实际阻抗外,还多了一部分由过渡电阻引起的附加阻抗。

这里认为IA相自阻抗Z1A的阻抗角θ1已知,且附加阻抗的角度θ=arg(IK/) 可以根据已知电气量计算得到,那么根据式(16) 可以很容易算出故障阻抗的实部ZR和虚部ZX。
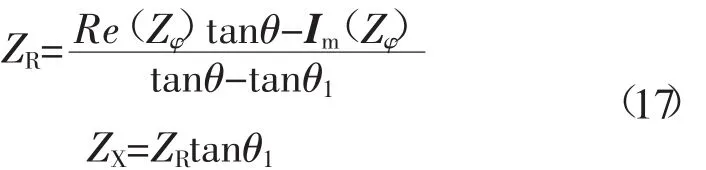
3 实例仿真计算分析
以山西某实际工程为例,利用PSCAD/EMTDC软件对图2所示的双端共母线不换位同塔双回线路模型进行仿真。仿真系统电源电势为330 kV,M侧系统正序阻抗为0.458+j5.228 9 Ω,零序阻抗为0.754+j3.283 Ω,N侧系统正序阻抗为1.091 4+j12.45 Ω,零序阻抗为 1.729+j7.524 7 Ω。
输电杆塔为伞形杆塔,6回线路采用垂直排列方式,呼高28 m,总高度47.1 m。输电导线型号为 4×LGJ-400/35,分裂间距 450 mm,外径26.82 mm,直流电阻为0.0738 9 Ω/km;地线型号为 JLB20A-80,外径 11.40 mm,直流电阻为1.078 8 Ω/km。
3.1 传统带零序补偿距离保护算法应用于不换位同塔双回线时的动作性能分析
依据《110~750 kV架空输电线路设计规范》说明,当线路长度不超过100 km时,可以不换位。因此本例仿真模型中设定输电线路长度为100 km长,相序布置方式为常见的逆相序排列IABCIICBA,且全程不换位。此处线路正序阻抗、零序阻抗及线间零序互阻抗取该线路理想换位时的数值,分别为 0.020 2+j 0.276 2,0.354 1+j 0.922 Ω及0.111 3+j 0.215 3 Ω。 在线路15~85 km区段内不同位置点设置单相接地故障、单回线相间故障及跨线故障,然后分别依据式(2)、式(4) 和式(6) 来计算不同故障类型下的故障阻抗,通过定义测量阻抗误差等于(ZX-/Z来表征距离保护的动作性能,这里,ZX为测量阻抗的虚部,Z为线路实际阻抗的虚部。3种故障类型下的计算阻抗误差如表1—表4所示。
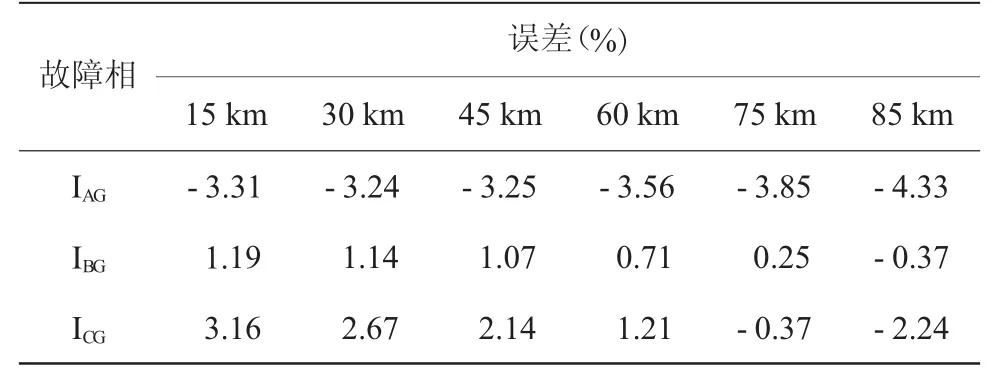
表1单相接地故障测量阻抗误差
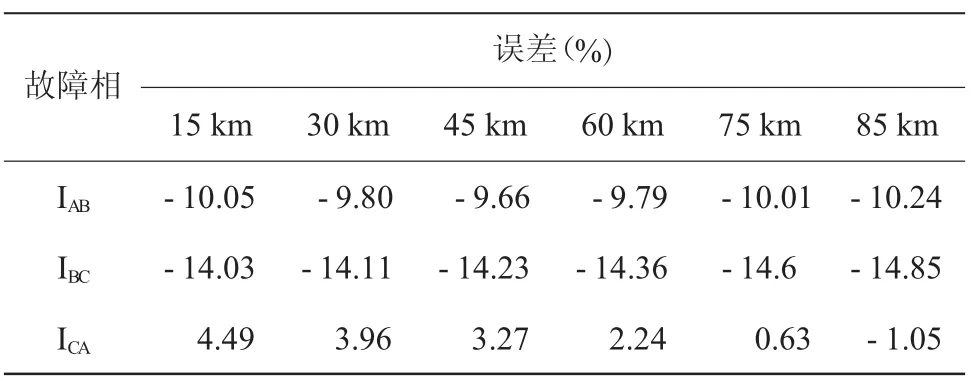
表2 单回线相间不接地故障测量阻抗误差

表3 单回线相间接地故障测量阻抗误差

表4 同塔双回线跨线故障测量阻抗误差
从表1—表4中可以看出,对于不换位同塔双回线,单相接地故障和跨线故障的测量阻抗误差较小,可以沿用传统带零序补偿算法或者是开发更安全的距离保护算法。相间故障时测量阻抗误差较大,本例中呈现出较大的负误差,有可能造成超越现象,而在其他的相序布置方式下还可能呈现出较大的正误差,从而严重缩短其I段保护范围。因此对于相间故障,一种改进方法是基于既定的相序布置方式调整其保护定值,另一种方法是寻找受线路不对称性影响较小的距离保护算法。
3.2改进距离保护算法应用于不换位同塔双回线时的动作性能分析
前面已经叙述了适用于不换位同塔双回线各种故障类型的距离保护算法,这里通过实例给以验证。同样采用3.1节的仿真模型,把线路延长至150 km来加大研究其适用范围,在线路15~135 km区段内每隔15 km设置故障点,研究不同故障类型下的距离保护动作性能。首先给出不换位同塔双回线的单位六相阻抗矩阵如下。
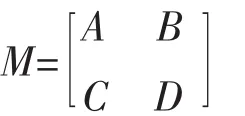
A、B、D分块矩阵在下面分别给出,C矩阵是B矩阵的转置。

基于已知的六相阻抗矩阵,首先计算不换位同塔双回线的线间零序互感Zm、线路的正序阻抗Z1和零序阻抗Z0。Zm取矩阵B所有元素的平均值为0.111 2+j0.203 8 Ω,Z1和Z0由式 (12)计算得到为 0.020 0+j 0.259 0 Ω 和 0.354 6+j0.956 5 Ω。然后根据第2节所提的方法计算不同故障类型下的测量阻抗值,并对不同故障类型下距离保护的I段按上面给定方式整定,得到对应故障类型下的距离保护动作特性如图3—图7所示。
从图3—图7不换位同塔双回线不同故障类型下的距离保护动作性能可以看出,本文所提距离保护算法计算得到的测量阻抗能较好地跟踪实际阻抗,不会造成明显的保护范围缩短或超越现象,极大地改善了线路不对称性对传统带补偿距离保护动作性能的影响。

图3 不换位同塔双回线IA相接地故障

图4 不换位同塔双回线IAB相故障

图5 不换位同塔双回线IAB-G相故障
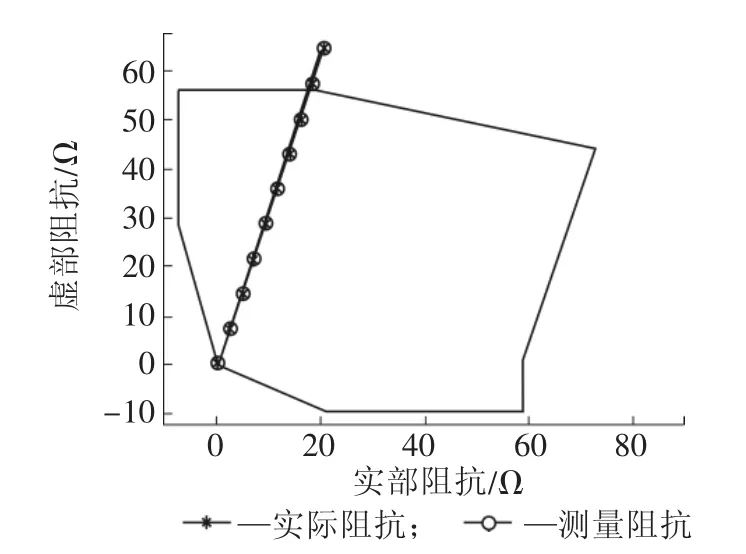
图7 不换位同塔双回线IA相经100 Ω过渡电阻接地故障
4 结语
a)同塔双回线路不换位时,各序分量之间均存在电气耦合,因此会给传统的带邻线零序电流补偿的距离保护算法带来一定的影响。传统的接地距离和跨线故障距离保护算法受参数不对称性影响较小,在不换位线路中可以考虑继续沿用;相间阻抗继电器受线路不对称性影响较大,在不同的相序排布下,可能会使保护范围严重缩短或超越,在工程中可以通过调整保护定值或寻找更优算法来防止距离保护的不正确动作。
b)针对不换位同塔双回线故障情况下的电气耦合特性,本文直接使用两回线电气量及六相阻抗矩阵对故障回路列写电压平衡方程,推导出适用于不换位同塔双回线各种故障类型下的距离保护算法。该算法简单、统一且性能良好,确保了不换位同塔双回线在不同故障类型、故障位置下距离保护均能正确动作。
[1] 隆茂,李田刚,安然然,等.不换位线路参数不对称对距离保护的影响分析 [J].电力系统保护与控制,2014,42(22)∶90-94.
[2] 王安宁,陈青,周占平,等.改进的相分量法求解同杆双回线故障新算法 [J].电力系统自动化,2009,33(13)∶58-62.
[3] AndréDarósFilomena,HartsteinSalim,MarianaResener,etal.Ground distance relaying with fault-resistance compensation for unbalanced systems[J].IEEETrans.PowerDel.,2008,23 (3):1319-1326.
[4] Vijay H.Makwana,Bhavesh R.Bhalja.A new digital distance relaying scheme for compensation of high-resistance faults on transmission line [J].IEEE Trans.Power Del.,2012,27(4): 2133-2140.
[5] Zhen Yu Xu,G.Xu,Li Ran,et al.A new fault-impedance algorithm for distance relaying on a transmission line[J].IEEE Trans.Power Del.,2010,25(3):1384-1392.
[6] Sang-Hee Kang,Yong-Jin Ahn,Yong-Cheol Kang,et al.A fault location algorithm based on circuit analysis for untransposed parallel transmission lines [J].IEEE Trans.Power Del.,2009,24(4): 1850-1856.
Research on the Distance Protection Performance for Common-tower Un-transposed Double-circuit Transmission Lines Based on Six-phase Parameter Information
ZHANG Shifeng,YANG Yunlei,CHANG Xiao
(State Grid Shanxi Electric Power Research Institute of SEPC,Taiyuan,Shanxi030001,China)
When a fault occurs on un-transposed double-circuit transmission lines,the measurement of impedance is not only affected by mutual inductance between the parallel lines,but also influenced by coupling effects between positive,negative and zero sequence generated by fault lines,which makes it difficult to satisfy the requirement of distance protection.The distance protection algorithm which is adaptable to various fault types occurred on the un-transposed common-tower double-circuit transmission lines is derived to form voltage equation for the fault loops by directly using electrical quantities of the parallel lines and six-phase impedance matrix.Theoretical analysis and numerical simulation performed by PSCAD show that the algorithm has an excellent distance protection performance,which can withstand a greater degree ofasymmetryand bigtransition resistance.
un-transposed common-tower double-circuit transmission lines;six-phase impedance matrix;transition resistance;distance protection
TM755
A
1671-0320(2017)05-0014-06
2017-07-10,
2017-08-06
张世锋(1989),男,山西五台人,2015年毕业于西安交通大学电力系统及其自动化专业,硕士,从事同塔双回输电技术、电能质量、新能源场站无功电压控制技术工作;杨赟磊(1990),男,山西朔州人,2015年毕业于武汉大学电力系统及其自动化专业,硕士,助理工程师,研究方向为电力系统运行与控制、电能质量分析及治理、新能源并网检测及管理;常 潇(1987),男,山西榆社人,2013年毕业于英国斯特拉斯克莱德大学电力系统及其自动化专业,博士,工程师,研究方向为储能技术、电能质量、新能源涉网实验技术。
