一类具有充分下降性修正的DL共轭梯度法

2017-11-16张莉林

重庆工商大学学报（自然科学版） 2017年6期

关键词：共轭收敛性常数

张莉林

(重庆师范大学数学科学学院，重庆 401331)

一类具有充分下降性修正的DL共轭梯度法

张莉林

(重庆师范大学数学科学学院，重庆 401331)

基于DL共轭梯度方法,提出了一类修正的DL方法来解决无约束优化问题.该方法相对于DL共轭梯度方法具有一个更好的性质,即在强Wolfe线搜索条件下搜索方向具有充分下降性;证明了该方法在强Wolfe线搜索条件具有全局收敛性.

共轭梯度法; 强Wolfe线搜索; 充分下降性；全局收敛性

0 引言

考虑无约束极小化问题：

minf(x),x∈Rn

(1)

其中,f:Rn→R是连续可微函数.

共轭梯度法是求解大规模无约束优化问题的一个重要方法，其迭代公式为

xk+1=xk+αkdk

(2)

(3)

其中步长αk通过某种线搜索计算得到,dk为搜索方向,gk=▽f(xk),βk∈R为共轭参数,选取不同βk产生不同的共轭梯度法.

经典的共轭梯度法有FR[1]方法, HS[2]方法, PRP[3]方法和LS[4]方法, 其表示方法如下:

其中‖·‖表Euclidean数,yk-1=gk-gk-1.

在文献[5]中戴彧虹和廖立志提出了截断形式DL方法:

(4)

其中常数t>0,sk-1=xk-xk-1.

在文献[6]中程云龙等人基于文献[5,7]提出了一类共轭梯度方法：

(5)

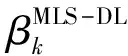
在文献[8]中杜学武等人提出了一个修正的LS方法:

(6)

本文受文献[6,8]的启发,提出了一类新的修正的DL共轭梯度公式:

(7)

记由式(2)(3)(7)构成的共轭梯度法为NVLS*DL方法.

为了分析该方法的全局收敛性，采用强 Wolfe 线搜索：

(8)

(9)

其中0<δ<σ<1.

1 全局收敛性

假设A 水平集Ω={x∈Rnfx≤fx1}有界, 即存在一个常数B>0, 使得‖x‖≤B，x∈Ω, 其中x1是初始点.

假设B 在水平集Ω的邻域Ν中,f连续可微且梯度函数g是Lipschitz连续的, 即存在一个常数L>0, 使得∀x,y∈Ω，

‖gx-gy‖≤L‖x-y‖

(10)

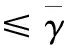
(11)

搜索方向dk具有下降性和充分下降性分别为

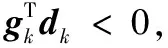
(12)

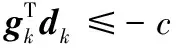
(13)

其中常数c>0.

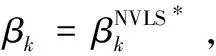
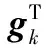
(14)

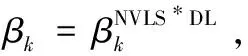
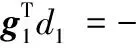
(15)

及引理1得：

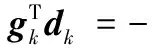
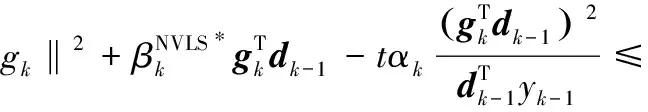
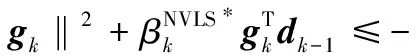
(16)

取式(13)中的c=1-2σ<1 , 则充分下降条件式(13)成立.

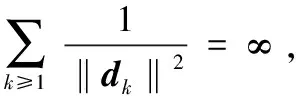
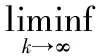
(17)

由引理2和引理3, 参照文献[6,10]中类似的证明方法可以证明下面的引理4.

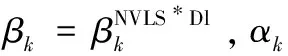
‖gk‖≥γ,∀k≥1

(18)

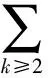
证明令

则由式(3)对∀k≥2, 有：

uk=γk+δkuk-1

(19)

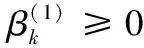
‖γk‖=‖uk-δkuk-1‖=‖δkuk-uk-1‖

(20)

则有：

‖uk-uk-1‖≤‖1+δkuk-1+δkuk-1‖≤‖uk-δkuk-1‖+‖δkuk-uk-1‖=2‖γk‖

(21)

由强Wolfe线搜索条件(9)式和式(15)可得：

(22)

由假设A有‖sk-1‖=‖xk-xk-1‖≤‖xk‖+‖xk-1‖≤2B,以及式(11)(22)可得：

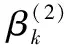
(23)

由式(21)和式(23)以及引理3则有：

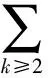
(24)

性质*[6]考虑迭代公式为式(2)式(3)的共轭梯度法, 假设对∀k≥1都有

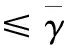
(25)

若对任意k, 都存在常数b>1,λ>0使得

βk≤b

(26)

以及

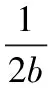
(27)

则称该方法具有性质*

下面将证明本文提出的NVLS*DL方法具有性质*

由式(15)以及引理2可知：

c(1-σ)‖gk-1‖2≥(1-σ)cγ2

(28)

文献[8]中引理4.1证明了

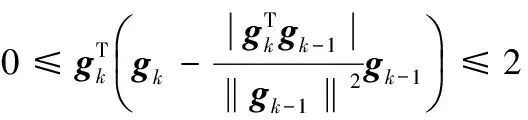
再由式(10)(11)(28)以及引理2证得的充分下降条件成立可得：

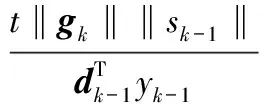
(29)

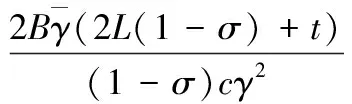
(30)

则NVLS*DL方法具有性质*[6].

设Ν*定义为正整数集合, 对于λ>0和正整数Δ，定义

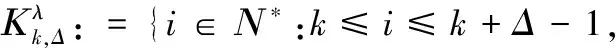
(31)

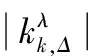
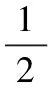
(32)

该引理的证明与文献[5]中的引理3.5类似.文献[5]中假设了满足充分下降条件(13), 本文不需要这个假设，在强Wolfe线搜索下NVLS*DL方法产生的搜索方向dk具有充分下降性.

根据上面的引理，下面来证明NVLS*DL方法的全局收敛性.

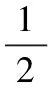
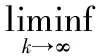
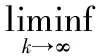
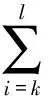
(33)

由式(33)，uk=1和假设A可得:

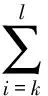
(34)

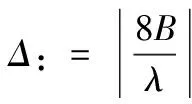
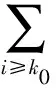
(35)

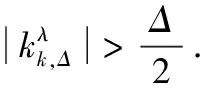
对任何指标i∈k,k+Δ-1,由Cauchy-Schwartz不等式和式(35)可得:

(36)

由式(35)和式(36)，在式(34)中令l=k+Δ-1，可得：

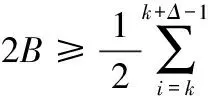
(37)

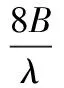
[1] FLETCHER R, REEVES C. Function Minimization by Conjugate Gradients[J]. Computation, 1964,7(2): 149-154

[2] HESTENES M R, STIEFEL E L. Methods of Conjugate Gradients for Solving Linear Systems[J]. J Res Nat Bur Standards, 1952 (49): 409-436

[3] POLAK E, RIBIRE G. Note Sur La Convergence De Methods de Directions Conjugées[J]. Rev Fr Inf Recherche Opertionelle, 1969(3): 35-43

[4] LIU Y, STOREY C. Efficient Generalized Conjugate Gradient Algorithms(part 1)[J]. J Optim Theory Appl, 1991,69(7):129-137

[5] DAI Y H , LIAO L Z. New Conjugacy Conditions and Related Nonlinear Conjugate Gradient Methods[J] Appl Math Optim, 2001 (43): 87-101

[6] CHENG Y L , MOU Q , PAN X B. A Sufficient Descent Conjugate Gradient Method and Global Convergence [J]. Optimization Methods and Software, 2016(31): 577-590

[7] WEI Y S , WEI Z X, HUANG H. A Note About WYL’s Conjugate Gradient Method and Its Applications[J]. Applied Mathematics and Computation, 2007(2): 381-388

[8] XUEWU D, PEMG Z, WENYA M. Some Modified Conjugate Gradient Methods for Unconstrained[J]. Journal of Computational and Applied Mathematics, 2016,305:92-114

[9] DAI Y H , HAN J , LIU G. Convergence Properties of Nonlinear Conjugate Gradient Methods[J]. SIAM Journal on Optimization, 1999,10(2) 345-358

[10] AO W B. Global Convergence for a Modified DY Conjngate Gradient Algorithm[J].Journal of Chongqing Technology and Business University(Natural Science Edition),2013,30(10):17-20

A Class of Modified DL Conjugate Gradient Method with Sufficient Descent

ZHANGLi-lin

(College of Mathematical Science, Chongqing Normal University, Chongqing 401331, China)

Based on the DL conjugate gradient method, a class of modified DL conjugate gradient method is proposed to solve unconstrained optimization problems. Compared with DL conjugate gradient method, the given method has a better property that search direction possesses the sufficient descent condition under the stonger Wolfe line seach. This paper proves the global convergence of the given method under the stonger Wolfe line seach.

conjugate gradient method;stronger Wolfe line seach; sufficient descent condition; global convergence

O157