基于IGS方法的最佳分类数研究*

2017-11-16张正军

重庆工商大学学报（自然科学版） 2017年6期

关键词：理工大学灰度聚类

窦婷，张正军

(南京理工大学理学院, 南京 210094)

基于IGS方法的最佳分类数研究*

窦婷，张正军**

(南京理工大学理学院, 南京 210094)

针对选择Gap Statistic(GS)方法估计聚类数能够得到数据集的粗略分类，但不能进一步对数据集进行细分类这一问题，对GS方法进行改进；将Gap统计量引入到ISODATA算法中，提出了IGS模型；实证表明，IGS模型不仅可以实现数据的细分类，而且通过IGS模型估计数据集的最佳分类数准确率明显高于原GS模型。

Gap Statistics；IGS模型；聚类数；ISODATA算法

0 引言

2000年，Tibshirani R[1]等在K-means方法基础上提出了用Gap Statistic(GS)方法估计数据集的最佳聚类数，该方法提出之后，就引起了广泛关注和应用。GS方法从统计学的角度解释并通过理论证明了样本数据的合理分类数的有效性。通过大量的仿真实验，GS方法比其他算法在估计最佳聚类数方面要好。

2003年，Mei 和Lajbcygier等[2]通过将GS方法与传统方法进行比较，分析了日本投资者共有的投资模式，发现通过GS方法有较多的优点。2005年，张正军，黄陈蓉等[3]通过样本灰度数据分布的差别从而定义了多尺度的图像灰度间隙,首先提出了反分布函数概念,在此基础上又建立了图像边缘检测的多尺度灰度Gap统计模型。2006年，李娜[4]对Gap统计量进行改进修正，计算出一维情况下具体Gap统计量的表达式，从而减少了计算量。2007年，Mingjin Yan[5]通过把类内离差程度总和变成每一类的平均离差程度之和的方法，使得每类离散程度的表示不受类内样本数量影响，从而更能体现出类内的相似度，使得GS方法更具有稳定性。2008年，岳士宏等[6]通过类内离差程度的二阶差分作为最佳聚类数的一个评判标，故而省去了选择参考分布，使算法变得简单有效。

GS方法可以适用于硬聚类，同样也可适用于模糊聚类。2007年，Sentelle C等[7]把GS方法的思想应用于FCM方法上，提出了FGS模型，该模型可以更好地刻画出某些模糊数据集的聚类特征。2008年，Arima C等[8]在FGS模型基础上对其进行改进，并提出了MFGS模型，该模型适应于基因表达数据集。2011年，童波[9]又对FGS模型进行了不同改进，提出了相应的MFGS模型，并且把该模型应用在图像分割中。2013年，刘倩[10]接着提出了WGS及DWGS模型，对原始灰度图像进行了合理的分割。

针对传统GS方法不能对数据集进行细分类的不足，对GS方法进行改进从而提出相应的改进模型IGS，通过它估计出数据集的最佳分类数，并且将GS模型和IGS模型在聚类收敛速度和聚类准确率两方面进行比较。

1 GS模型

传统的Gap Statistic方法的核心思想是：首先，选择一个参考分布，通过参考分布生成参考数据集；其次，将待分类数据的离散程度和参考数据集的离散程度进行比较，将分类数作为自变量，建立一个Gap统计量；最后，通过分析Gap统计量关于聚类数的变化情况来确定最佳聚类数[9]。

传统的Gap Statistic的主要内容有：假设数据集已由K-means算法聚成k类：C1,C2,…,Ck，nr=Cr。令

(1)

其中，Dr表示聚类r中所有数据两两之间的距离平方和。再令

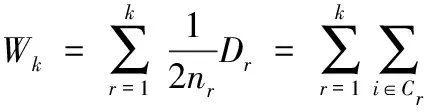
(2)

其中，Wk表示k类离差程度的总和。由此定义Gap统计量：

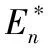
(3)

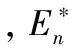
2 IGS模型

使用传统的GS方法能够得到数据集的粗略分类，然而不能进一步对数据进行细分类。GS方法基于K-means聚类算法，在 K-means 算法中聚类数值K是事先给定的，但是这个K值的选定是非常难以估计的。对于高维或者海量的数据集事先不知道应该分成多少个类别才最合适，然而ISODATA算法可以通过类的自动合并和分裂[11]，得到较为合理的类型数目K。IGS模型即将Gap统计量引入到ISODATA算法[12-15]中。通过IGS方法对类别数相对较多的数据集聚类可以得到数据集的细分类，比如Glass数据集，GS方法对Glass数据集进行聚类得到的最佳聚类数为2，而通过IGS方法对Glass数据集进行聚类得到的最佳聚类数为7。考虑到ISODATA算法相对K-means算法时间略长些，故对生成的参考数据集依旧用K-means进行聚类。

IGS模型的算法步骤如下：

Step1 通过ISODATA算法对数据集进行聚类，得到各类别的类内离差平方和Wk；

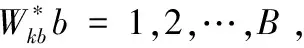
(4)

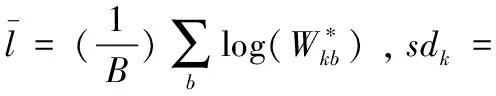
Gap(k)≥Gap(k+ 1)-sk + 1

(5)

3 仿真实验及分析

通过几组实验与原始GS方法进行比较，验证提出的IGS方法的可行性与优越性。对参考分布的生成进行蒙特卡洛模拟，采用的聚类算法是ISODATA算法。通过这个算法得出的聚类结果较稳定，故采用Gap曲线图来分析IGS方法的结果。

(1) 实验数据集，实验使用的UCI机器学习数据库的4个测试聚类算法的常用数据集的描述见表1。

表1 实验所用的UCI数据集描述

(2) IGS方法的实验结果和分析。本实验采用UCI数据库中的Iris，Glass，Haberman和Ionoshpere 4个数据集，采用GS和IGS两种方法对以上数据集进行聚类并估计出最佳聚类数，检验IGS方法的可行性。

对于ISODATA算法来说，参数的选取直接影响到聚类的效果，对于Iris数据集参数选取如下：θN=5，θS=1.8，θC=1.5，L=2，I=100，从图1中可以看出既可以用传统GS方法估计出最佳聚类数，所得的最佳聚类数为3，也可以用所介绍的IGS方法估计出最佳聚类数，得到的最佳聚类数为3。

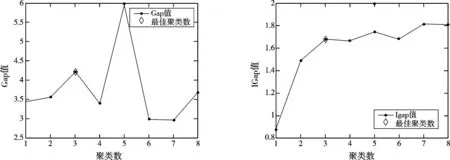
图1 Iris数据集中Gap和IGap随聚类数的变化曲线Fig.1 Iris data set Gap and IGap change Curve with the number of clusters

对于Glass数据集，ISODATA算法选取的参数为θN=5，θS=2.5，θC=0.2，L=2，I=100，由图2可知，IGS方法得到的估计值为7，而GS方法得到的估计数为2，这是因为ISODATA算法可以自动低分裂和合并，对于类别较多的样本而言，可以通过IGS方法对其进行细分类。

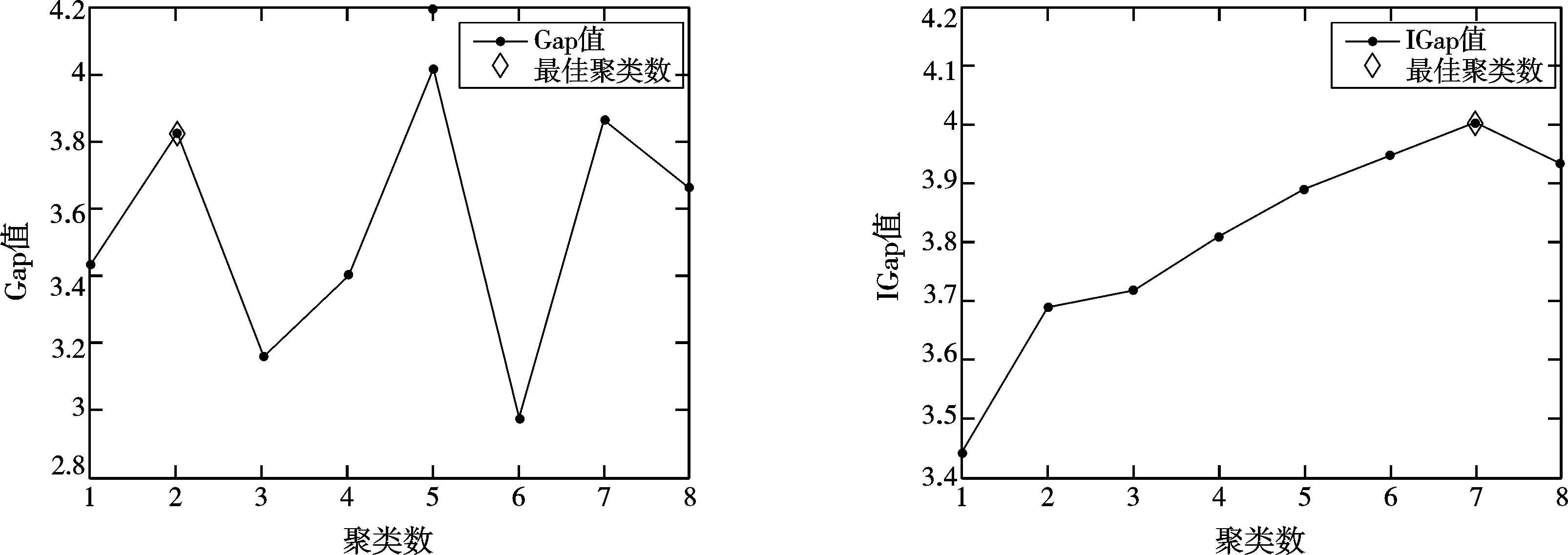
图2 Glass数据集中Gap和IGap随聚类数的变化曲线Fig.2 Glass data set Gap and IGap change curve with the number of clusters

对于Haberman数据集，ISODATA算法选取的参数为θN=5，θS=15，θC=0.1，L=2，I=100。由图3可知，通过GS方法得到的最佳估计数为3，通过IGS得到的最佳估计数为2，IGS得到的聚类数较为准确。由于ISODATA算法较K-means算法而言，初始中心的选取对ISODATA算法的影响不大[16]，而且该算法能够实现自动分裂与合并，可以看出可准确地将Iris数据集分为3类。

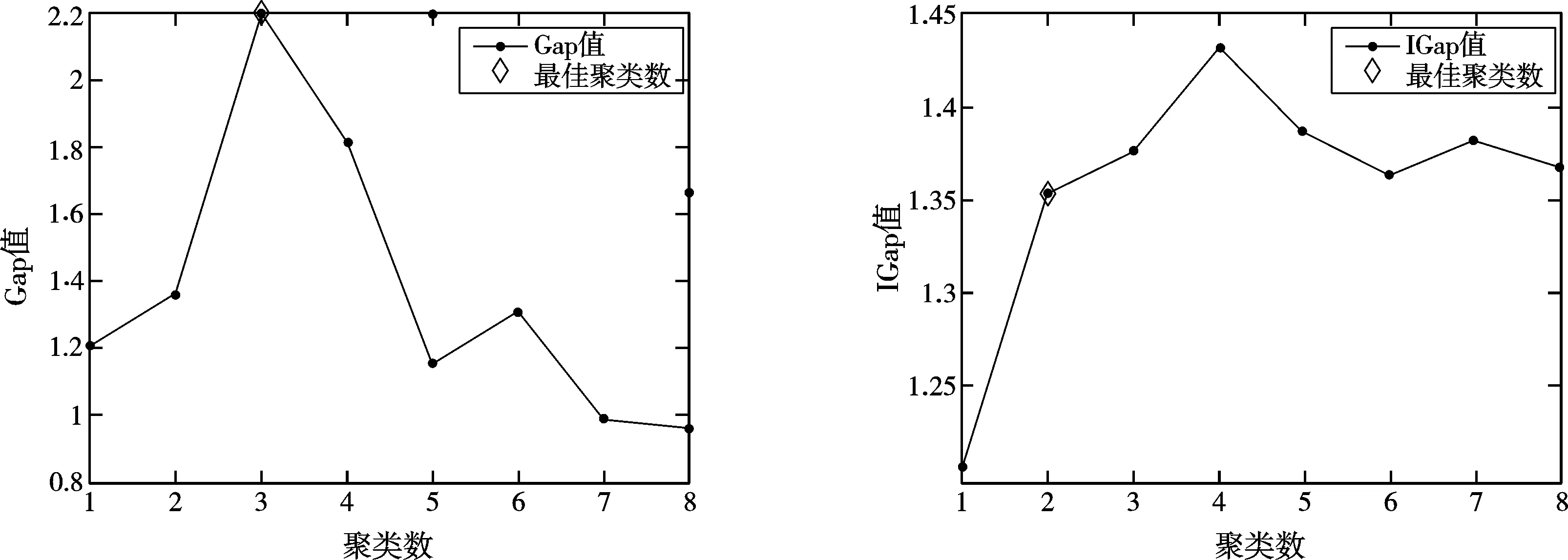
图3 Haberman数据集中Gap和IGap随聚类数的变化曲线Fig.3 Haberman data set Gap and IGap change Curve with the number of clusters

对于Ionosphere数据集，ISODATA算法选取的参数为θN=10，θS=0.9，θC=3，L=2，I=100。由图4可知，通过GS方法得到的最佳聚类数为3，而通过IGS方法可以将Ionosphere数据集准确地分为2类。

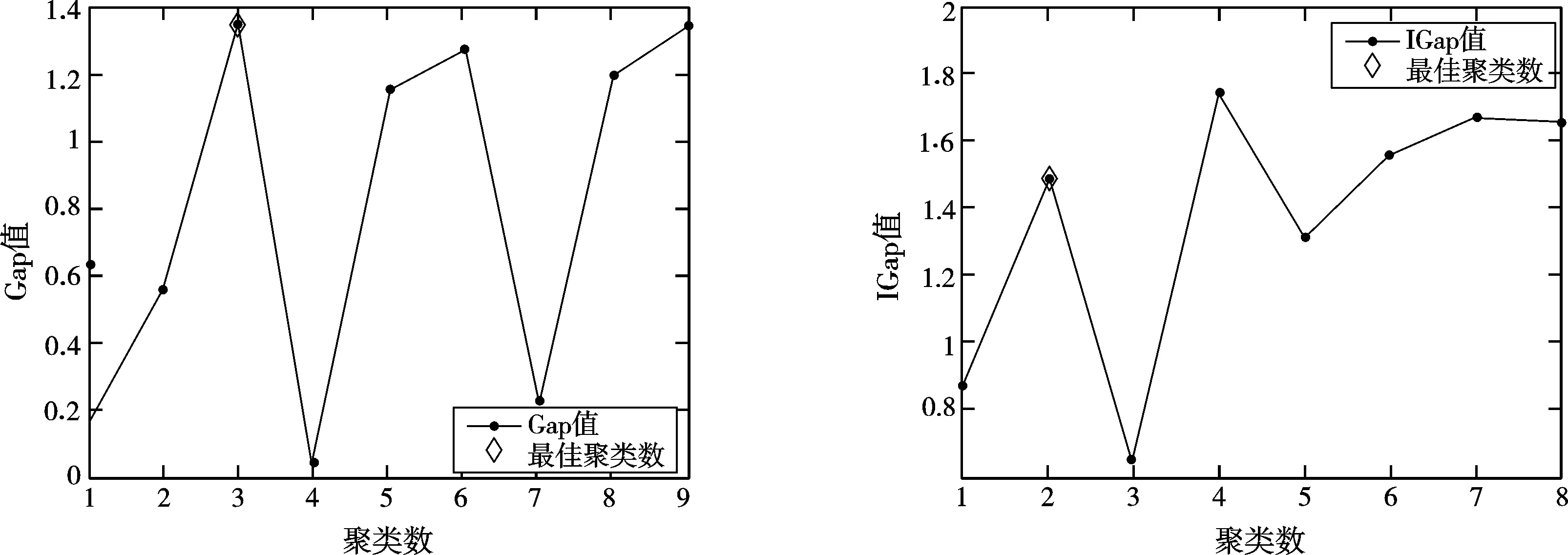
图4 Ionosphere数据集中Gap和IGap随聚类数的变化曲线Fig.4 Ionosphere data set Gap and IGap change Curve with the number of clusters

4 IGS模型与传统GS模型性能比较

实验采用2种评价指标对聚类结果进行评价：对表1中4个数据集，分别利用GS和IGS重复运行50次，估计出最佳聚类数的正确率p，算法运行时间t。

从表2中可以看出，IGS方法和GS方法对数据集聚类所用的时间差不多，但是通过表3发现IGS方法估计数据集最佳聚类数的准确率比传统GS方法要高，改进后的算法较好。

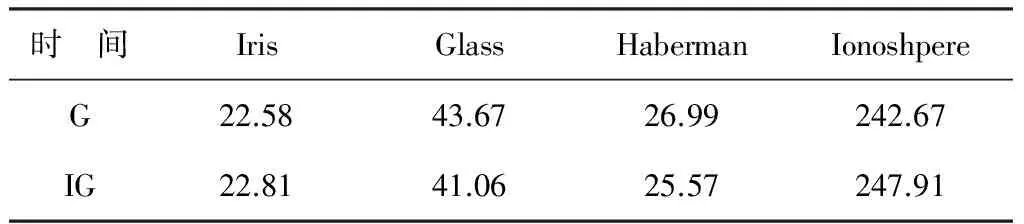
表2 数据集聚类所用的时间

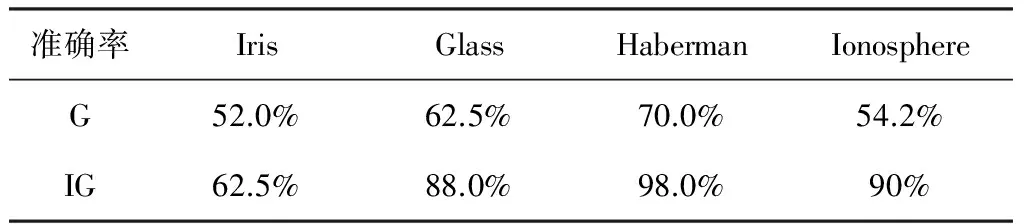
表3 数据集最佳聚类数估计的准确率

5 结论

对传统的GS模型进行改进，提出了IGS模型，运用IGS模型对数据集进行聚类，IGS方法可以实现对数据集的细分类。实证表明，通过IGS方法估计数据集最佳聚类数准确率比较高。

[1] TIBSHIRANI R, WALTHER G, HASTIE T. Estimating the Number of Clusters in a Data Set via the Gap Statistic[J]. Journal of the Royal Statistical Society, 2000, 63(2):411-423

[2] LAJBCYGIER P, ONG M Y. Estimating the Number of Mutual Fund Styles Using the Generalized Style Classification Approach and the GAP Statistic[C]//Computational Intelligence for Financial Engineering, Hong Kong, China, 2003

[3] 黄陈蓉, 张正军, 吴慧中. 图像边缘检测的多尺度灰度Gap统计模型[J]. 中国图像图形学报, 2005, 10(8):1018-1023

HUANG C R, ZHANG Z J, WU H Z. Multiscale Gray Scale Gap Statistical Model for Image Edge Detection[J].Chinese Journal of Image and Graphics,2005, 10(8):1018-1023

[4] 李娜. 基于GS方法的图像最佳分割的研究[D]. 南京:南京理工大学, 2006.

LI N.Research on image Segmentation Based on GS Method[D].Nanjing: Nanjing University of Science and Technology,2006

[5] YAN M, YE K. Determining the Number of Clusters Using the Weighted Gap Statistic[J]. Biometrics, 2007, 63(4):1031-1037

[6] YUE S H, WANG X X, WEI M M. Application of Two-Order Difference to Gap Statistic[J]. Transactions of Tianjin University, 2008, 14(3):217-221

[7] SENTELLE C, HONG S L, GEORGIOPOULOS M, et al. A Fuzzy Gap Statistic for Fuzzy C-Means[C]// Proceedings of the Eleventh IASTED International Conference on Artificial Intelligence and Soft Computing. ACTA Press, 2007

[8] ARIMA C, HAKAMADA K, OKAMOTO M, et al. Modified Fuzzy Gap Statistic for Estimating Preferable Number of Clusters in Fuzzy K-means Clustering.[J]. Journal of Bioscience & Bioengineering, 2008, 105(3):273-281

[9] 童波. 基于MFGS方法图像最佳分割数的研究[D]. 南京: 南京理工大学, 2011

TONG B.Research on the Optimal Number of Image Segmentation Based on MFGS Method[D]. Nanjing: Nanjing University of Science and Technology,2011

[10] 刘倩. 基于GS方法的图像分割估计数的多信息动态研究[D]. 南京: 南京理工大学, 2013

LIU Q.Research on Information Dynamic Estimation of the Number of Image Segmentation Based on GS Method[D]. Nanjing: Nanjing University of Science and Technology,2013

[11] 李前进, 王寅龙, 李志祥,等. 基于直觉模糊的ISODATA算法[J]. 计算机工程与应用, 2012, 48(9):176-177

LI Q J,WANG Y L,LI Z X, et al. ISODATA Algorithm based on Intuitionistic Fuzzy[J].Computer Engineering and Applications,2012, 48(9):176-177

[12] 万建, 王继成. 基于ISODATA算法的彩色图像分割[J]. 计算机工程, 2002, 28(5):135-136

WAN J,WANG J C.Color Image Segmentation Based on ISODATA Algorithm[J].Computer Engineering,2002, 28(5):135-136

[13] 康永辉, 戴激光, 王广哲. 改进的自适应模糊ISODATA灰度图像分割算法[J]. 计算机工程与应用, 2016, 52(17):198-202

KANG Y H,DAI J G,WANG G Z.An Improved Adaptive Fuzzy ISODATA Algorithm for Image Segmentation[J].Computer Engineering and Applications,2016, 52(17):198-202

[14] 张丽娜, 姜新华, 那日苏. 基于改进的ISODATA算法的大样本数据聚类方法研究[J]. 内蒙古农业大学学报(自然科学版), 2013, 34(1):133-137

ZHANG L N,JIANG X H,NA R F.Research on Large Sample Data Clustering Method Based on Improved ISODATA Algorithm[J].Journal of Inner Mongolia Agricultural University (Natural Science Edition), 2013, 34(1):133-137

[15] 黄健元. 模糊ISODATA聚类分析方法的改进[J]. 南京航空航天大学学报, 2000, 32(2):179-183.

HUANG J Y.Improvement of Fuzzy ISODATA Clustering Analysis[J].Journal of Nanjing University of Aeronautics and Astronautics, 2000, 32(2):179-183

[16] 陈平生. K-means和ISODATA聚类算法的比较研究[J]. 江西理工大学学报, 2012, 33(1):78-82

CHEN P S.Comparative Study of K-means and ISODATA Clustering Algorithms[J].Journal of Jiangxi University of Science and Technology, 2012, 33(1):78-82

Research on the Optimal Number of Classification Based on IGS Method

DOUTing,ZHANGZheng-jun

(School of Science, Nanjing University of Science and Technology, Nanjing 210094, China)

According to the problem that Gap Statistics (GS) method can get rough classification of data sets and can not get the fine classification of data sets, this paper improves GS method by introducing Gap statistic into ISODATA algorithm and proposes IGS model. Empirical research indicates that IGS model can not only realize the fine classification of data but also can estimate the optimal number of classification of the data sets through IGS model whose accuracy is obviously higher than original GS model.

Gap Statistics; IGS model; cluster number; ISODATA algorithm

TP314