基于梯形二维语言变量相似度的多属性群决策方法*

崔文利, 平轶男, 王 熠, 徐立为

(安徽大学 数学科学学院，合肥 230601)

基于梯形二维语言变量相似度的多属性群决策方法*

崔文利, 平轶男**, 王 熠, 徐立为

(安徽大学 数学科学学院，合肥 230601)

针对评价信息为梯形二维语言变量的多属性群决策问题，提出了一种新的梯形二维语言变量的相似性测度并探讨其性质；基于相似性测度最大化准则构建了两个优化模型以分别求解多属性群决策问题中的专家权重和属性权重，进而提出一种新的基于梯形二维语言变量相似性测度的多属性群决策方法；最后通过实例验证了新方法的合理性和有效性.

多属性群决策; 梯形二维语言变量；相似度；权重

0 引 言

在多属性群决策过程中，由于客观事物的复杂性和不确定性，决策信息往往以语言变量、区间语言信息来表达，但考虑决策专家的知识背景和能力，在实际给出评价值时的肯定度也有很大影响，文献[1]在传统语言评价信息的基础上，增加了一维反映决策者主观评价自信程度的第二维语言评价信息，提出了二维语言评价信息的概念.二维语言评价信息在决策过程中能够很好地反应决策者在评价时存在的不自信的心理行为，因此二维语言评价信息的研究引起了众多学者的关注[2-10].例如，文献[2]定义了二维语言Chouquet积分算子，并将VIKOR方法应用到二维语言决策问题中，文献[3]提出了基于证据推理和VIKOR的二维语言多准则群决策问题；文献[4]提出了二维语言广义依赖加权平均算子并将它们运用于决策中，文献[5]定义了二维不确定语言Power算子等.

传统意义上的二维语言变量，只是两个简单的，定性的语言评价信息，而在处理定量的评价信息中还存在不足.因此文献[6]提出梯形二维语言变量的概念，梯形二维语言变量包含二维评价信息，其中第一维语言为梯形模糊数，用来表示对象的定量评价值，第二维语言评价信息用来表示决策者定性判断的可靠性，进一步的，探讨了梯形二维语言变量运算法则、期望值与排序方法，并且提出了基于梯形二维语言的一般广义集成算子、Bonferroni算子和优先集成算子，研究了基于3种集成算子的多属性群决策方法.因梯形二维语言变量能够很好地将定性与定量语言评价信息表示出来，进而更好地表达评价信息的不确定性，而目前对于梯形二维语言变量的研究相对较少，因此对梯形二维语言变量的相关测度的研究具有一定价值和意义.

考虑在一些大型的决策问题中，往往需要多个决策者共同参与，群决策是研究的重要方面.方案排序与属性权重密切相关，合理确定属性权重也成为多属性决策的一个重要内容，但是目前关于梯形二维语言变量的相似测度的研究较为少见，因此提出了基于梯形二维语言变量的相似测度群决策方法.

1 预备知识

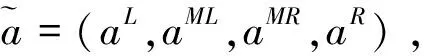
(1)

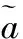
定义2[8]称S={s0,s1,…,sl-1}为含有l个语言标度的语言评价集，si为语言标度或语言变量(i=0,1,…,l-1)，l为语言标度集S中语言变量或语言标度的个数，一般取奇数.

例如，语言标度为3、5、7的语言评价集可分别表示为

S={s0,s1,s2}={差,中,好}

S={s0,s1,s2,s3,s4}={差,较差,中,较好,好}

S={s0,s1,s2,s3,s4,s5,s6}={差,较差,中下,中,中上,较好,好}

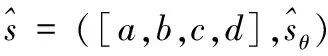
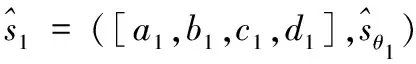
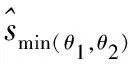
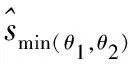
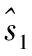
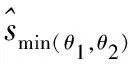
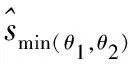
a2,b2,c2,d2≠0

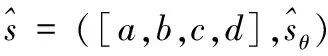
(2)

2 梯形二维语言相似性测度

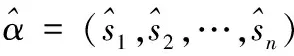
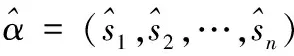
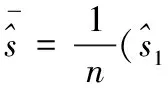
(3)

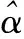
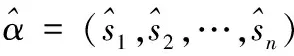
则称

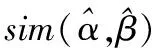
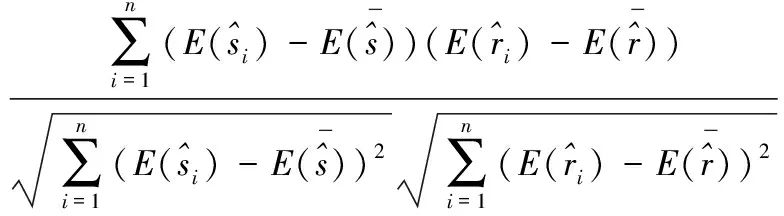
(4)

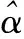
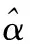
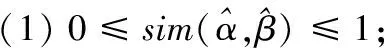
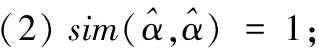
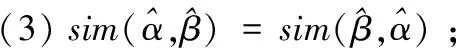
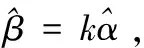
证明性质(1)、性质(2)、性质(3)易证，下证性质(4)：

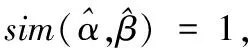
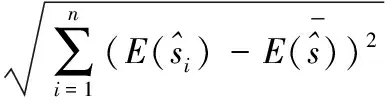
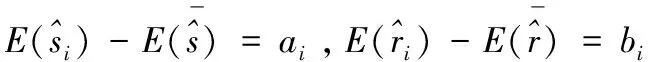
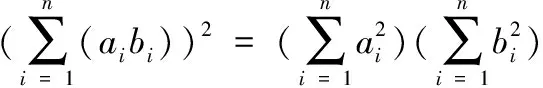
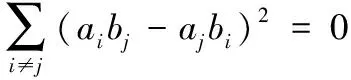
即需证明aibj=ajbi(i≠j)

故需证明bi=kai，即

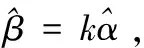
3 基于梯形二维语言相似度的模糊群决策方法

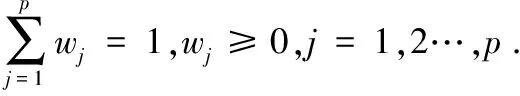
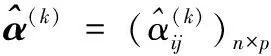
(1) 效益型属性：

其中，M=

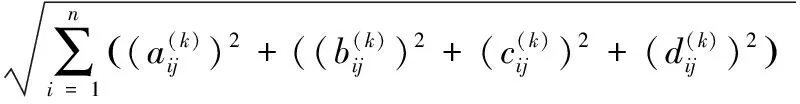
(2) 成本型属性：

(6)

其中，N=

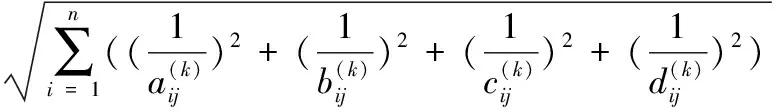
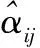
(7)

进一步，令

其中，

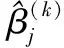
则称

(8)

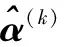
对模糊多属性群决策而言，综合决策矩阵越贴近各个专家的决策矩阵，则表明各个专家决策信息的集成效果越好，故可以最大相似度为准则建立如下模型：

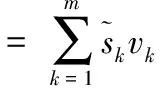
(9)

模型(9)为非线性规划模型，故可用Matlab来进行求解.

(10)

为方案xi的综合评价值.

则可以把

(11)

看成各方案的不同属性值与综合评价值之间的相似测度.各个方案的综合评价值越贴近于每个方案不同属性值的评价信息，则表明不同属性值的评价信息集成效果越好，故可以最大相似度为准则建立如下模型：

(12)

模型(12)也为非线性规划模型，可通过Matlab或LINGO软件求解.

3.4 基于梯形二维语言相似度的模糊群决策方法 基于梯形二维语言相似度的模糊群决策方法步骤如下.

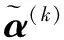
Step2 利用模型(9)求解决策专家权重向量v=(v1,v2,…,vm);

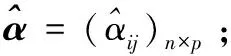
Step4 利用模型(12)求解属性权重向量w=(w1,w2,…,wp);

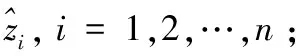
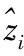
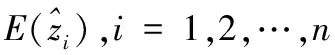
Step8 结束.

4 实例分析

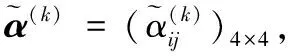
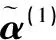
表1 d1专家的决策矩阵

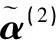
表2 d2专家的决策矩阵

表3 d3专家的决策矩阵

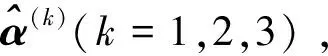
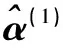
表4 专家d1标准化决策矩阵

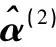
表5 专家d2标准化决策矩阵

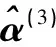
表6 专家d3标准化决策矩阵

利用模型式(9)，其中vi∈[0.1,0.4]，求出各个专家的权重向量为v=(0.4,0.2,0.4)，并利用式(7)得到群体的综合决策矩阵见表7.

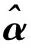
表7 群体综合决策矩阵

利用模型式(12)，其中wi∈[0.1,0.4]，求出各个属性的权重向量为w=(0.1,0.4,0.4,0.1)，并利用式(10)得到各个公司集成不同属性信息的综合评价值为

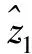
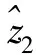
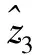
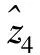
利用式(2)计算4家公司综合属性值的期望值为

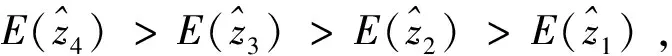
文献[6]提出的基于梯形二维语言变量的多属性群决策方法中，仅考虑专家权重和属性权重均已知多属性决策问题，而本文中提出的基于梯形二维语言相似度的群决策方法是在专家权重和属性权重未知的情况下，充分运用评价信息求出最优方案.

5 结束语

基于梯形二维语言变量，定义了一种新的相似测度，并提出了基于梯形二维语言相似度的模糊多属性群决策方法.实例表明了其方法的有效性和可行性.梯形二维语言变量同时拥有二维语言变量和梯形模糊数的优点，在处理模糊性方面更具有实用性，因此在决策领域有更好的前景.

在未来的研究中，可以进一步将该方法拓展至其他语言环境中[9-11]，例如二元语义、犹豫语言等，并做进一步的比较研究，同时，还可以应用于绿色供应商选择、组合预测研究、网络基金评审等社会活动中.

[1] 朱卫东，周广中，杨善林. 基于二维语言评价信息的群体决策方法[J]. 系统工程，2009, 27(2): 113-118

ZHU W D, ZHOU G Z, YANG S L. Group Decision Making Method Based on 2-dimensional Linguistic Evaluation Information[J]. System Engineering, 2009, 27(2):113-118

[2] 吴良刚，文丽. 基于Choquet积分和VIKOR的二维语言多准则群决策方法[J]. 模糊系统与数学，2015，29(6): 46-55

WU L G, WEN L. 2-dimension Linguistic Multi-criteria Group Decision Making Method Based on Choquet Integral and VIKOR[J]. Fuzzy Systems and Mathematics, 2015，29(6): 46-55

[3] 吴良刚，文丽. 基于证据推理和VIKOR的二维语言多准则群决策方法[J]. 计算机应用研究，2016，33(6): 1697-1702

WU L G, WEN L. 2-dimension Linguistic Multi-criteria Group Decision Making Method Based on Evidence Reasoning and VIKOR[J]. Application Research of Computers, 2016，33(6): 1697-1702

[4] LIU P D, QI X F. Some Generalized Dependent AGgregation Operators with 2-dimension Linguistic Information and Their Application to Group Decision Making[J]. Journal of Intelligent & Fuzzy Systems, 2014, 27(4): 1761-1773

[5] LIU P D, YU X C. 2-Dimension Uncertain Linguistic Power Generalized Weighted Aggregation Operator and Its Application in Multiple Attribute Group Decision Making[J]. Knowledge-based Systems, 2014, 57(2):69-80

[6] 石兰兰. 基于梯形二维语言变量的信息集成算子研究[D]. 济南:山东财经大学,2016

SHI L L. The Research on Aggregation Operators Based on Trapezoidal Two-Dimension Linguistic Numbers[D]. Jinan: Shandong University of Finance and Economics, 2016

[7] 李荣钧. 模糊多准则决策理论与应用[M]. 北京:科学出版社,2002: 23-34

LI R J. Theory and Application on the Fuzzy Multiple Attribute Decision Making [M]. Beijing: Science Press, 2002: 23-34

[8] ZADEH L A. The Concept of Linguistic Variable and Its Applications to Approximate Reasoning(Part I)[J]. Information Science,1975(8):199-249

[9] ZHOU L G, CHEN H.Y. The Induced Linguistic Continuous Ordered Weighted Geometric Operator and Its Application to Group Decision Making[J]. Computers & Industrial Engineering, 2013, 66: 222-232

[10] 吴群，吴澎，周礼刚. 基于联系数的区间二元语义模糊多属性群决策方法[J]. 重庆工商大学学报(自然科学版), 2016, 33(1): 1-8

WU Q, WU P, ZHOU L G. Interval 2-tuple Linguistic Fuzzy Multiple Attributes Group Decision-making Based on Connection Variables[J].Journal of Chongqing Technology Business University (Natural Science Edition), 2016, 33(1): 1-8

[11] 吴群，吴澎，周元元，等. 2TLCGPOWA算子及其在多属性群决策中的应用[J]. 计算机工程与应用，2017, 53(3): 47-53

WU Q, WU P, ZHOU Y Y,et al. Generalized 2-Tuple Linguistic Connection Power Ordered Weighted Average Operator and Its Application to Multiple Attribute Group Decision Making[J]. Computer Engineering and Applications, 2017, 53(3): 47-53

Multiple Attribute Group Decision Making Method Based on SimilarityDegree of Trapezoidal Two-dimension Linguistic Numbers

CUIWen-li,PINGYi-nan,WANGYi,XULi-wei

(School of Mathematical Science, Anhui University, Anhui Hefei 230601, China)

With respect to multiple attribute group decision making (MAGDM) problem where the evaluation information is in the form of trapezoidal two-dimension linguistic numbers (T-2DLNs), a new similarity measure for T-2DLNs is proposed, and its properties are discussed as well. The two optimization models are constructed to solve experts’ weight and attributes’ weight in MAGDM on the basis of maximizing similarity measure, and then a new MAGDM method via similarity measure for T-2DLNs is presented. Finally, a numerical example indicates that the proposed method is effective and feasible.

multi-attribute group decision making; trapezoidal two-dimension linguistic numbers; similarity degree; weight;

C934

A

2017-04-26；

2017-06-04.

国家自然科学基金(71371011,71301001, 71501002)；安徽省优秀青年人才支持计划； 安徽大学博士科研启动基金； 安徽省自然科学基金(1508085QG149)； 安徽省高校省级自然科学研究重点项目(KJ2015A379)； 合肥学院科研发展基金(12KY02ZD)；安徽省哲学社会科学项目(AHSKQ2016D13)；安徽大学科研训练计划项目(KYXL2016006)；安徽大学创新训练项目(201610357119，201610357347，201610357348，201610357349).

崔文利(1996-)，女，安徽宿州人，从事预测与决策研究.

**通讯作者：平轶男(1986-)，女，安徽淮南人，硕士研究生，从事预测与决策研究. E-mail: 1492021090@qq.com.

责任编辑：罗姗姗