基于层次分析法的数学专业资料订阅策略研究

2017-11-16

图书馆界 2017年5期

关键词：使用量院系分析法

(宝鸡文理学院数学与信息科学学院，陕西宝鸡 721013)

谢

燕

(宝鸡文理学院数学与信息科学学院，陕西宝鸡 721013)

专业学术资料的订阅受到资源有限，资金缺乏，主体、客体约束等因素制约，而专业学术资料的订阅在现代高校的发展中有重要作用，目前，国内针对具体学科的专业资料订阅策略极少。针对这一现状，引入层次分析法，以数学学科为例建立期刊订阅策略评价指标体系模型，从期刊价格、期刊影响因子、期刊使用量、期刊内容四个方面构建层次结构模型，进行综合质量排序分析，结合院系学科实际，得出合理的专业资料订阅策略。这个订阅策略对其他院系的专业资料订阅同样具有参考价值。

专业资料；层次分析法；订阅策略

1 引言

随着高等学校学生扩招的结束，很多院校都相继转入内涵式的发展。为提高学科的实力和竞争力，高校都在实施人才强校的战略。人才引入后都涉及一个非常重要的问题，即如何利用资源的有限性为专业人才提供尽可能多的专业方向资料，这个问题成为近年来困惑学科资料订阅的难题。首先，学科资料的订阅具有鲜明的特征：专业指向性很强、阅读者人数较少甚至寥寥无几，这决定了资料订阅如果不合理会造成资源的极大浪费。其次，专业学科资料必须订阅，现代社会飞速发展，学科的发展也是日新月异，如果没有跟踪学科前沿的学术资料，这个学科就无法在现代高校大发展中立于不败之地。再次，专业资料处在教学科研的第一线，能够直接为教师备课、教学和科研提供专业辅助，为本学科的研究生提供专业方向发展最前沿的信息，具有明显的专业性和针对性。另外，虽然现代社会网络发达，但对于专业性很强的学术性学科而言，网络的作用很有限，因为网络只能提供面向大众的公共知识或者专业基础知识，对学术前沿很难跟踪，几乎是网络出现的知识都是大众化的知识，已经不具有专业性了。

目前对国内期刊订阅策略的分析，一般都是理论分析，有用模糊决策分析的，也有从读者角度研究的“读者推荐系统”，但极少有针对具体的学科期刊给出订阅策略。本文以某师范大学数学学科的专业性特点为例，运用层次分析法给出具体的专业学术资料订阅策略。

2 基于层次分析法的数学专业资料订阅策略

层次分析法是美国运筹学家托马斯·塞蒂于20世纪70年代提出的一种系统分析方法，它将定性的方法与定量的方法相结合，将复杂问题分解为若干层次和若干因素，在各个因素之间进行两两比较，最终得到不同的问题解决方案的权重，为最佳的选择提供理论依据。此方法具有简单实用的特点，适合多目标、多准则、多时期的系统评价。

2.1 数学专业资料订阅的约束条件及评价指标体系的选择

数学学科资料室主要订阅基础数学方向、计算数学方向和应用数学方向的专业资料，另外，还有一些广义数学应用方面的资料，如系统工程、电子学报、通信学报以及各种学报。如何合理分配资源，使有限的资金订阅到最有用的期刊资料，是目前迫切需要解决的问题。专业期刊订阅和其他期刊订阅一样，受到很多约束条件。首先是经费约束，众所周知，高校图书馆、资料室最为紧缺的就是经费，为了尽可能充分地利用经费，只能根据现有资金能力尽量多地订阅那些能有效提供本院系读者群所需信息的期刊。其次是期刊订阅的客体约束，包括期刊的影响因子、质量、内容、发行量，出版及时性、区域等等。再次，期刊的主体约束因素也很重要，师范类院校数学期刊订阅的教师主体群大致分为四类：基础数学方向、计算数学方向和应用数学方向，另外还有部分研究生。

从以上期刊订阅的约束条件可以看出，价格因素具有重要影响，经费直接决定了订阅期刊的数量。期刊的影响因子决定着该期刊的阅读量和期刊的使用范围。而期刊的内容决定了该期刊是实际影响好还是人为的只为提高影响力，这一点通过调查实际阅读的一线教师和研究生可得到答案。期刊使用量和本学科的师资专业方向密切相关。因此，本文选择期刊价格、期刊影响因子、期刊内容和期刊使用量作为期刊订阅策略评价指标体系的构成要素。

2.2 评价模型的建立与检验

2.2.1 构建层次结构模型。期刊订阅策略的层次结构模型分三层：以期刊的综合质量为总目标层，以期刊价格、期刊影响因子、期刊使用量、期刊内容为准则层，以各种期刊为方案层。本文以数学学科的6种期刊(P1：《中国科学》，P2：《数学学报》，P3：《数学物理学报》，P4：《计算数学》，P5：《数值计算与计算机应用》，P6：《数学进展》)为例，给出订阅的排序策略。那么层次分析法结构如图1所示。

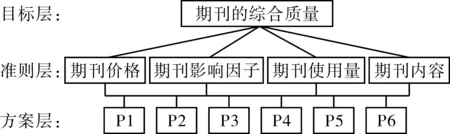
图1 层次分析法结构图

2.2.2 构造对比较阵，计算权向量并做一致性检验。通过查阅期刊价格、影响因子，利用文中赋值表的尺度(见表1)邀请院系教师和研究生填写问卷，调查这6类期刊的使用量，并结合专家打分的方法，确定各种专业期刊的准则层。各因素的得分值如表2所示。

重要性标度含义1表示两个元素相比,具有同等重要性3表示两个元素相比,前者比后者稍重要5表示两个元素相比,前者比后者明显重要7表示两个元素相比,前者比后者强烈重要9表示两个元素相比,前者比后者极端重要2,4,6,8表示上述判断的中间值倒数若元素i与元素j的重要性之比为bij,则元素j与元素i的重要性之比为bij=1bij

期刊编号及名称价格影响因子使用量内容P1(《中国科学》)1740.62258P2(《数学学报》)1000.45347P3(《数学物理学报》)600.4837P4(《计算数学》)300.73268P5(《数值计算与计算机应用》)150.45236P6(《数学进展》)200.27225

从层次结构模型的第2层(准则层)开始，用成对比较法和1-9比较尺度构造成对比较矩阵，直到最下层。首先结合经费实际情况赋予价格、影响因子、使用量以及内容四个方面的两两比较，比如，调查发现，教师普遍认为影响因子要比价格强一倍，那么价格对影响因子的比例就是二分之一，同时调查发现，价格和使用量影响不大，内容是价格的四倍。这样可构造价格对于其他三个因素的成对比较矩阵

。类似的方法可以建立其他成对比较矩阵

(

=1,2,3,4)，然后利用matlab中对成对比较矩阵进行归一化处理，并进行一致性检验。设

为一致性指标，其中，

=0,1,2,3,4)，分别计算出λmax，进一步解得

。

阶数123456789RI0.000.000.580.901.121.241.321.411.45

由于

=0,1,2,3,4)，其中，由表3知

的值，故可计算出

，从而可判断出是否通过一致性检验，若不能通过一致性检验，则需对

进行修正；若通过一致性检验，则计算λ=λmax的特征向量为

。通过计算矩阵

，得到λ=0.0813，归一化的特征向量为：

=(0.4440,0.8166,0.3340,0.1565)其中，

=0.0271，

=0.0301<0.1，故可通过一致性检验。同理可计算出成对比较矩阵

，

的权向量最大特征值λmax和一致性指标

，结果列入表4。

i1234w(6)i0.43610.23860.21740.19510.25060.10750.17390.17070.15040.14900.13040.17070.07520.22720.26090.19510.03760.17340.13040.14640.05010.10430.08700.1219λmaxi65.237066CIi00.112600CRi00.090800

由表4可知以上成对比较矩阵均可通过一致性检验。

类似的，对6种期刊的综合质量进行评估，其计算结果见表5。

权向量准则C0.4440C10.8166C20.3340C30.1565C4组合权向量P10.43610.23860.21740.19510.4916P20.25060.10750.17390.17070.2838P30.15040.14900.13040.17070.2587P40.07520.22720.26090.19510.3366P50.03760.17340.13040.14640.2248P60.05010.10430.08700.12190.1556

由表5可知，这几类期刊综合质量排序依次为：P1(《中国科学》)，P4(《计算数学》)，P2(《数学学报》)，P3(《数学物理学报》)，P5(《数值计算与计算机应用》)，P6(《数学进展》)。

类似的，对所需要订阅的期刊，我们也可以按照层次分析法进行排序，为合理订阅资料提供帮助。

3 结合实际的数学专业资料订阅策略讨论

由于期刊价格决定着院系期刊的订阅数量，期刊影响因子决定了期刊的实际阅读量以及影响力，而期刊使用量是和某个院系的实际预览数密切相关，期刊内容在院系的使用和教师与学生的学习方向息息相关。所以在评判订阅策略时我们选取这四个关键因素。

前述调查对象以基础教育和师范教育为主的院校，数学学院具有鲜明的特征，数学教育以基础教育为主，也就是以传统的基础数学为主，主要从事纯粹数学的理论研究，计算和应用数学的基础理论研究，对实际应用往往关注较少，这类院系的教师和学生的学术创作也是以基础理论为主。另一方面，许多院系在资源有限的约束下，考虑到教师和学生的单打独斗在学术上很难有较大突破，于是舍弃学术研究很弱的方向，开始整合学术研究方向，形成学术团队，增强学术竞争力，在经费预算上就优先支持学术实力更强的学术团队，这样期刊的订阅就更具有针对性，所以期刊订阅策略不单单是一个排序的问题。比如，从上述的层次分析法可以看出，尽管《数学学报》杂志在我国国内知名度遥遥领先，但是在本文调查的数学学院教师结构以及学术团队里，该杂志的使用量其实并不高，而《计算数学》杂志虽然知名度不是很高，但是教师团队中计算数学人数多而且实力强，使用量明显较多。所以，在期刊的征订方面，在经费有限的前提下，应该优先考虑教师和学生的查阅量这个因素，以查阅量为主导来订购，在查阅量排序的情况下，对于相近的期刊整合出学术团队需要的全部期刊，可能有的期刊使用量并不多，但是对整个学术团队具有一定的实用价值，也应该订阅。比如在数学学院里，吉林大学学报信息与计算科学版实际查阅量并不大，但是调查发现，该学院计算数学团队教师觉得该期刊应该订阅。

4 结论

从以上的分析研究可以看出，订阅数学专业期刊前要先调查期刊查阅量，然后对学术团队所需期刊进行整合，优先考虑学术团队的订阅，然后再对其他期刊用层次分析法进行排序，按顺序进行订阅。每年应该预留少量的经费，以便教师需要其他期刊的个别文章时，可以购买电子期刊，打印和复印给资料室留存。这样既能满足广大教师和学生的查阅量，也能较好地增强学术团队的实力，提高院系的知名度。这个订阅策略对其他院系同样具有较好的参考价值，只要调查查阅信息以及学术团队情况，应用层次分析法分析就可以给出订阅策略。

[1]电子期刊与纸质期刊比较浅析[EB/OL][2014-09-02].http：∥www.docin.com/p-543327395.Html.

[2]杨正先.谈纸质期刊与网络期刊的优缺点[J].科教导刊(上旬刊)，2013(11)：240-241.

[3]楚存坤，孙思琴，韩丰谈.基于层次分析法的高校图书馆学科服务评价模式[J].大学图书馆学报，2014(6)：86—90.

[4]扈凤梅.如何加强学校图书资料的管理[J].新课程学习，2010(1)：32.

[5]聂峰英.网络环境下的纸质期刊订阅策略[J].图书馆学研究，2003(5)：50—52.

[6]代小秋.对专业期刊订阅模式的思考[J].编辑学报，2015，27(2)：170—172.

[7]邢玲.注重期刊订阅管理为新课程教学科研服务[J].中小学图书情报世界，2006(1)：37—38.

[8]谭观音，李继宏.高校图书馆期刊选订的模糊决策[J].现代情报，2003(9)：149—151.

[9]何年琴，刘允.基于CRM的期刊报纸订阅读者推荐系统[J].图书情报工作，2005(11)：67—69.

[10]阮晓青，周义仓.数学建模引论[M].北京：高等教育出版社，2013：211—226.

G258.6

1005-6041(2017)05-0036-04