基于爆破漏斗试验的岩石可爆性研究

曹小康 刘 平 蔡向昇 杨荣强

(中国建筑第五工程局有限公司，湖南 长沙 410004)

基于爆破漏斗试验的岩石可爆性研究

曹小康 刘 平*蔡向昇 杨荣强

(中国建筑第五工程局有限公司，湖南 长沙 410004)

根据利文斯顿爆破漏斗理论，分析了影响爆破漏斗形成的相关因素，并在蒲津路爆破工程项目中设计了系列单孔爆破漏斗实验，实验收集的数据用SPSS软件进行回归分析，对现场使用的乳化炸药的特征曲线、爆破漏斗体积与埋深的关系、漏斗半径与炸药埋深的关系进行了分析研究，求出最佳埋深，应用实验结果指导工程实践，得到了较好的爆破效果。

爆破漏斗,可爆性,利文斯顿理论

0 引言

如今爆破作为破碎岩石的主要手段，在工程上得到广泛应用，比如采矿、水利、城市建设等方面都有涉及爆破；但是岩石具有复杂的内部结构，节理裂隙情况差异很大，现场的情况各不相同，使得爆破参数的选取不能完全按照经验来取；炸药在岩石内部爆炸时，会使破碎的岩石向自由面方向抛掷，形成爆破漏斗，它作为我们研究爆破作用机理的主要途径，在实施爆破作业前一般需要对岩石进行试爆，有必要的话通过爆破漏斗试验来测量岩石的可爆性，以及临界埋深、最佳孔距等参数，以保证爆破作业效果能达到预期要求。

为了减少爆破器材的耗费，指导项目的施工，提高爆破效果和经济效益，控制爆破的振动效应，对项目现场岩石进行漏斗试验的研究。

1 项目基本情况

1.1项目概况

蒲津路改造二期道路等级为城市主干路Ⅰ级，路线全长为4 640 m；桩号K1+600～K2+240段道路红线宽35 m，桩号K2+240至五合大桥段K6+240道路红线宽68 m。K1+800～K2+040段周边环境较复杂，北面约40 m为邕江，东面为开阔地，南面约17 m～60 m有村庄民房，西面约120 m为邕宁区人民医院。K1+800～K2+040段临近三条道路，北面开挖区坡下为仙鹤路、西面57 m为和平三街、南面42 m为吉祥巷。K1+800～K2+040段北侧约10 m有沿路的电线、光缆经过，K2+550附近上方约70 m有高压线横跨。

此工程采取的施工方式主要为爆破开挖，这就需要我们根据现场试验求出合理的爆破参数，以指导爆破施工，所以设计了爆破漏斗试验。

1.2项目特点及要求

本项目为C级土石方爆破，爆破施工部分区域附近300 m内有民房、电缆、道路、高压线等民用设施存在，根据《爆破安全规程》需提高一个级别，部分民房稳固性较差，房屋与山体相接，为砖结构和砖混结构，建设年代长，抗震能力差；所需开挖的岩体主要是石灰岩，厚层块状构造，岩体较完整，岩体基本质量等级为Ⅲ级，局部岩层节理裂隙较发育，分布有宽0.1 m～0.5 m不等的小裂隙。岩体表面有植被和表土覆盖，仅有少量岩石露出。

爆破作业不能影响周边民用设施的安全；爆破为松动爆破，不能产生过多飞石，需要对岩石进行可爆性研究，优化爆破参数，达到理想的爆破效果。

2 理论基础

2.1岩石的剪切破坏理论

岩石的剪切破坏理论[1]认为爆炸作用通过产生冲击波和爆生气体对周围环境产生破坏，其中以爆生气体的作用为主，在最小抵抗线方向上，岩石的阻力最小，所以朝抵抗线方向岩石受到剪切力被破坏并被抛掷，继而形成漏斗型坑洞。

爆破作用指数n是爆破漏斗半径r与最小抵抗线W之比，当n=1时为标准抛掷爆破，当n>1时为加强抛掷爆破，当n介于0.75～1之间时为减弱抛掷爆破，当n<0.75为松动爆破。

2.2利文斯顿理论

在控制爆破中，利文斯顿曾提出以能量平衡为准则的爆破漏斗理论，即炸药在岩体内爆炸时传给岩石能量的多少和速度的快慢，取决于岩石的性质、炸药性能、药包质量、炸药埋置深度和起爆方式等因素。

根据利氏理论，提出了炸药和炸药埋深的关系[2]：

Le=EbQ1/3

(1)

其中，Le为炸药埋置临界深度；Q为炸药量；Eb为岩石的变形能系数。

Eb的物理意义是在一定的装药量Q的条件下岩石表面开始破裂时岩石可能吸收的最大爆破能量。

在岩石性质、药包质量一定的情况之下，爆破作用的效果取决于药包埋置深度的大小，如果当药包的埋深达到某个深度时，形成的漏斗体积越大，而当药包埋深大于或小于埋深时产生的漏斗体积小，此时对于炸药爆破能力的利用率最高。

3 试验内容

装药量及炮孔间距和深度。

爆破漏斗的研究表明，当药包长径比不大于8时，其爆破作用与球型药包相当，本次实验装药量为200 g/孔，填入炮孔时长径比不超过8[3]。

必须保证相邻爆破漏斗不会相互影响，根据经验我们将相邻炮孔间距设计大于1.5 m，采用1.6 m为实验炮孔间距。

根据类似爆破漏斗试验的经验数据，我们设计在不同炮孔的深度下实验,炮孔垂直布置。采用1段非电雷管进行引爆。

4 数据的收集与处理

4.1爆破漏斗体积与漏斗直径的测量

以垂直炮孔轴线的平面，作为基准面，即取地面为基准面，在爆破前后，分别按10 cm×10 cm的网度测量漏斗轮廓线到基准面的距离，求出各测点的爆破深度，按抛物线法(辛卜生法)[4]计算求得漏斗各断面的面积Si。

Si=B/3[(Y0+Yn)+2(Y2+Y4+…+
Y2i+…)+4(Y1+Y3+…+Y2i+1+…)

(2)

其中，Si为漏斗某断面面积,m2；B为测点间距，B=0.1 m；Yi为第i点的爆破深度。

爆破后按相同的网度测量漏斗轮廓线距基准面的距离。求出测点的爆破深度，然后按棱台体体积计算公式计算出漏斗各断面的面积Si，最后按棱台体求得各漏斗的体积V。

(3)

4.2爆破漏斗半径的测量

爆破后，扣除漏斗口周围岩石片落部分，圈定漏斗的边界，然后以炮孔为中心，每隔45°角量取漏斗半径，取其8个测量值的平均值，再求出漏斗半径Ri作为本次爆破实验的漏斗半径。

4.3收集的数据

漏斗试验数据表见表1。

表1 漏斗试验数据表

4.4岩石可爆性的评价

利用SPSS软件将数据进行回归分析，分别对孔深L(x)与漏斗体积V(y1)、漏斗深度P(y2)与漏斗半径R(y3)和漏斗深度的数据进行拟合，得出各自的回归方程为：

y1=-816.121x2+934.573x-208.217

(4)

y2=-6.530x2+7.363x-1.489

(5)

y3=-1.621x2+1.838x-0.309

(6)

结合SPSS软件对实验数据的分析看得出，装药量一定的条件下，孔深和漏斗体积成二次关系，从拟合曲线图1～图3看出，当孔深为0.82 m时，爆破作用不产生抛掷岩石，不会形成爆破漏斗，可以认为当孔深为0.82 m时，岩体表面刚好开始破裂，所以临界埋深Ln=0.82 m。将其代入利文斯顿公式中：

Le=Eb×Q1/3

(7)

将公式变形为：

Eb=Le/Q1/3

(8)

求出Eb=1.4，由Eb的值可以看出为较难爆的岩石。

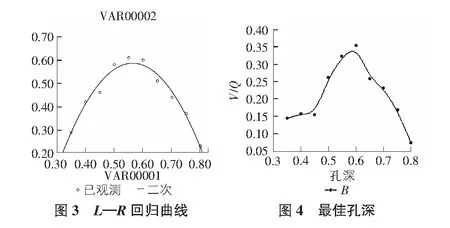
4.5最佳孔深的确定

从图1～图3中可以看出，在药包质量与岩石性质保持不变时，爆破作用所产生的漏斗体积存在最佳值，药包中心深度与V/Q的相关性呈抛物线型如图4所示，在孔深为0.65左右时，爆破效果达到最高值。在孔深为0.8 m时，岩石刚好破碎并不产生飞石，符合松动爆破的要求，所以0.8 m的孔深最佳。

5 结语

本实验将爆破漏斗试验用于研究岩石的可爆性，控制装药量不变，在不同孔深条件下对爆破漏斗的数据予以收集；利用SPSS软件进行回归分析，可得出如下经验：

1)求出Eb有助于选择合理的炸药单耗，可以为孔网参数的选择提供参考。选择合理的孔网参数及装药量，可以提高爆破的安全性，减少爆破飞石。

2)在药量一定的情况下，爆破漏斗体积的大小反映了炸药能量的利用率。爆破漏斗体积与孔深大致呈二次函数关系。

[1] 李守巨,刘迎曦,吴玉良.爆破漏斗形成过程的拉伸和剪切理论[J].岩石力学与工程学报,1996(15)：525-528.

[2] 金旭浩,卢文波.爆破漏斗理论探讨[J].岩土力学,2002(23):206-208,219.

[3] 张 生.爆破漏斗实验在中深孔爆破参数确定中的应用[J].现代矿业,2013(3)：8-10,40.

[4] 江飞飞,陈 良,李向东.爆破漏斗体积多方法测量及其比较分析[J].采矿技术,2013(13)：127-128,153.

Experimentalstudyonrockblastablitybasedonblastingcrater

CaoXiaokangLiuPing*CaiXiangshengYangRongqiang

(ChinaConstructionFifthEngineeringCo.,Ltd,Changsha410004,China)

According to the blasting crater theory preseted by Livingston, the factors influenced the formation of blasting crater are discussed, series of crater experiments of single hole blasting were performed in blasting project of Pujin road, the date from experimental design were analyzed by SPSS software, the relationship between blasting crater volume and change embedment depth, the relationship between crater vatius and charge enbedment depth have been discussed, the optimum depth has been found out. Applying the results to guide angineering practice, obtained the good blasting effect.

blasting craterl, blastablity, livingston theory

1009-6825(2017)28-0075-02

2017-07-24

曹小康(1984- )，男，工程师

刘 平(1964- )，男，工程师

TU458.2

A