RBF神经网络优化灰线性回归模型预测建模

赵亚红, 郝延锦, 丁建闯

(华北科技学院 建筑工程学院，北京 东燕郊 065201)

RBF神经网络优化灰线性回归模型预测建模

赵亚红, 郝延锦, 丁建闯

(华北科技学院 建筑工程学院，北京 东燕郊 065201)

针对建筑物地基沉降的机理以及RBF(Radial Basis Function,径向基函数)神经网络能够有效描述不确定性问题和解决复杂非线性问题等特点，通过反复试验，优化设计，建立了RBF神经网络，并用该网络优化灰线性回归预测模型，建立RBF灰线性组合预测模型。通过工程实例，比较分析了单一灰色模型、灰线性回归模型、RBF优化的灰线性回归模型的预测精度。结果表明，RBF优化后的灰线性回归预测模型精度优于灰色模型、灰线性回归模型，预测中误差达到0.0014 mm。径向基神经网络优化后的灰线性模型能更好地反映建筑物沉降的总体趋势及规律。

RBF；优化；灰线性回归模型；沉降预测

0 引言

在 工程建设的各个阶段，建筑物(或构筑物)所引发的安全问题都关系到人民的生命和财产，受到社会各界的广泛关注，因此变形监测与预测变得尤为重要[1]。为了研究建筑物变形趋势与规律，很多学者运用了各种各样的预测模型算法，有灰色理论、时序分析、马尔科夫理论、支持向量机、神经网络等，但实践证明单一的理论、方法或模型，很难对变形进行可靠性预测，因此单一模型改进以及多种组合模型广泛应用于建筑物变形预测中。组合模型可以扬长避短，兼具了各个单一模型的优点，被广泛的应用。

灰色GM(1,1)是利用最小二乘算法计算指数模型的参数，也是灰色理论中最简单的模型。很多专家学者通过大量的实践证明，灰色GM(1,1)对短期预测有较好的精度，但是对于数据中的异常情况，如跳变，难以考虑[2,3]。线性回归模型[4-6]按照事物发展规律，在各种条件相对稳定的情况下，对短期预测能够达到较理想的效果。RBF(Radical Basis Function)神经网络[7]是局部逼近型网络，“可以任意精度逼近非线性映射且结构简单、训练简洁、学习收敛速度快，它能够解决线性模型的限制问题，有效描述事物本身不确定性，多输入等复杂的非线性问题”。因此在时间序列分析、模式识别、非线性控制等领域被广泛应用。

本文以灰色GM(1,1)、线性回归模型和RBF神经网络理论为基础，建立了RBF优化的灰线性回归组合预测模型，并结合实际工程对建筑物沉降进行预测分析，验证组合模型的适用性、可靠性及精度。

1 RBF优化灰线性回归预测模型的建立

1.1 灰线性GM(1 1)

设有X(0)为一组原始观测序列

X(0)={x(0)(1),x(0)(2),x(0)(3),…,x(0)(k)}

对X(0)进行一次累加，生成新序列记作X(1)

X(1)={x(1)(1),x(1)(2),x(1)(3),…,x(1)(k)}

式中

由文献[2-4]中得到GM(1,1)预测模型方程：

(1)

式中为a发展系数，b为灰作用量，其形式可以记为：

(2)

用指数方程和线性回归方程累加进行拟合，建模过程详见文献[6、8-9],得到灰线性回归预测方程 ：

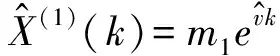
(3)

将(3)式累减得到灰色线性回归模型的预测值。由式(3)中可以看出当m1=0该模型为线性回归模型；当m2=0为传统灰色GM(1,1)模型。因此灰线性回归模型兼具了两种模型的优点。

1.2 RBF优化灰线性回归组合模型的建立

RBF神经网络是一种3层的前向网络。由输入层，带节点的隐含层和输出层三部分组成。隐含层节点视实际问题而确定，主要通过算法不断尝试调整节点个数。隐含层中神经元的变换函数即径向基函数。输出层对应输入层。由于RBF可以有效描述不确定问题，解决复杂的非线性问题[10-13]，因此可以利用RBF对灰线性回归预测模型残差进行修正、从而优化预测结果，提高预测精度。具体流程如图1所示。

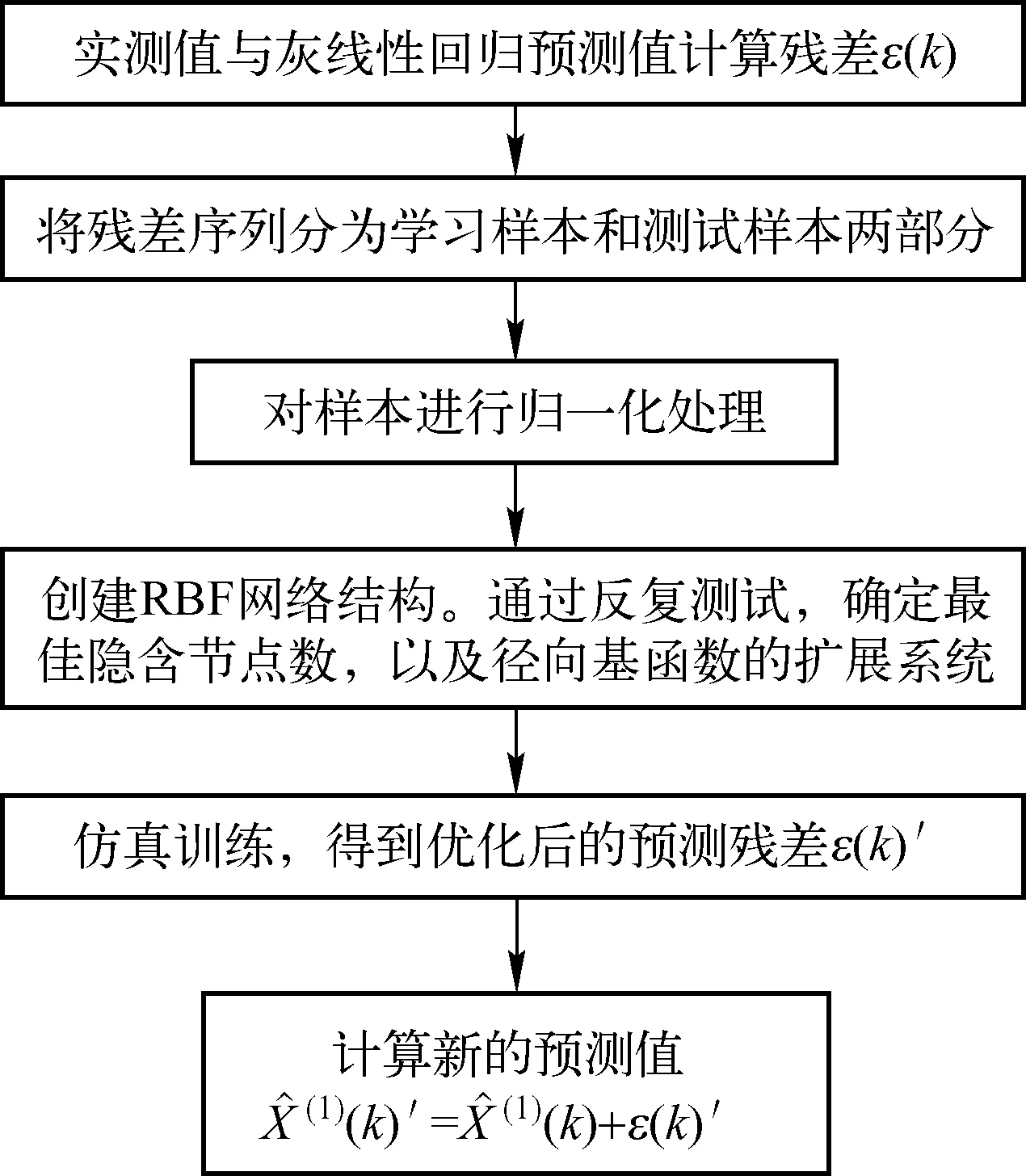
图1 RBF神经网络优化灰线性模型预测建模流程

2 预测模型的应用

为了验证模型的可靠性，以参考文献[8]中某地产开发公司新建居民楼，1#建筑物CJ1点沉降观测数据为例，分别利用传统的灰色GM(1,1)、灰线性回归、RBF修正灰线性回归模型进行建模预测，并对预测精度进行对比分析。

2.1 RBF神经网络结构的构建

在构建RBF神经网络过程中，关键就是隐含节点数以及径向基函数扩展系数SPREAD的确定。本文首先尝试创建SPREAD为1，隐含层节点数为 4，显示间隔为1的RBF网络。在创建过程中慢慢增加隐含节点数，直至网络输出误差达到预设值10-6为止，输出误差如表1所示。

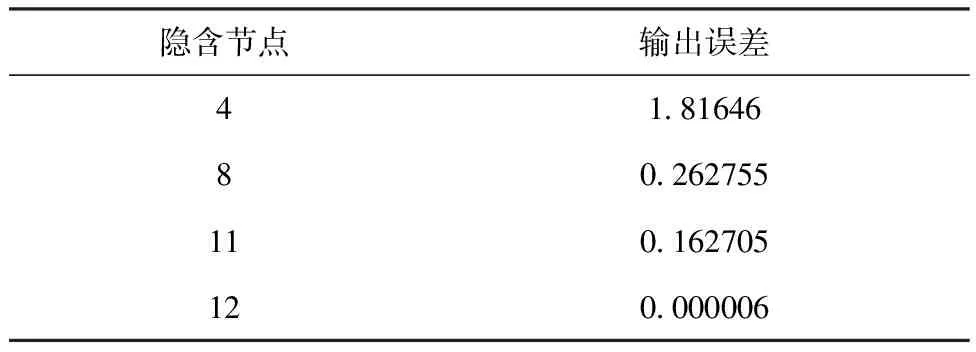
表1 不同隐含节点对应的输出误差

由表1可以看出，当隐含节点增至12时，网络输出误差达到目标值，是以最佳隐含节点数为12。接下来确定SPREAD值。SPREAD参数选择很重要，过小，可能造成过学习；过大，可能导致数值计算困难。因此在RBF神经网络设计过程中，须要确定SPREAD值就要进行反复试验以确定最优值。本文通过多次实验尝试，最终确定SPREAD为1。

2.2 RBF优化灰线性回归模型数据计算

表2 RBF修正灰线性残差结果 /mm

表3 各模型预测值及相对误差

3 整体精度评价与效果

针对灰线性回归神经网络预测模型精度，本文以平均绝对百分误差(MAPE)[14]、误差平方和(SSE)/中误差(RMSE)作为评定精度的指标。中误差反应误差分布的离散情况，在国际上也以中误差作为衡量精度的指标[15]，因此本文利用中误差评价各模型预测精度。精度分级见表4。各模型最终预测精度见表5。

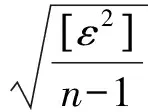
SSE=ε2

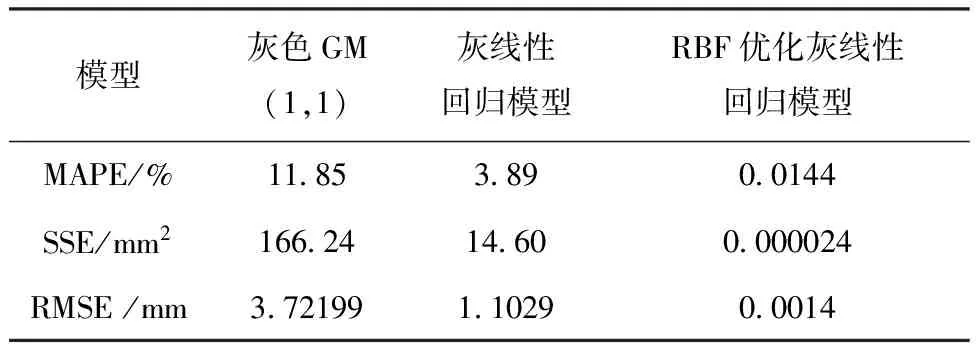
表5 模型精度比较

由表5可以看出，灰线性回归模型与RBF修正后的灰线性回归预测模型，都属于高精度拟合，但灰线性回归模型残差经RBF神经网络修正后，预测值精度得到显著提高，预测结果基本与实测值相符合。

4 结论

(1) 本文在线性回归模型、灰色GM(1,1)和RBF神经网络模型的基础上，利用RBF神经网络模型对灰线性回归模型进行了优化，构建了灰线性回归神经网络组合预测模型。

(2) 结合工程实例，利用RBF优化灰线性回归模型进行建筑物沉降预测。结果表明，优化后模型预测精度得到显著提高，优于传统的灰色GM(1,1)预模型和灰线性模型。预测中误差达到0.0014 mm，能够运用于建筑物沉降预测中。

[1] 张正禄,黄金义,文鸿雁,等.工程的变形监测分析与预报[M].北京:测绘出版社,，2007.11:6-8.

[2] 邓聚龙.灰色预测与决策[M].武汉:华中科技大学出版社，2002.

[3] 刘思峰，党耀国，方志耕.灰色系统理论及其应用[M].北京:科学出版社， 2004.

[4] CAO Wangcheng, LIU Zhiyu, ZHENG Lin. Application of gray neural network in the prediction of slope deformation[J]. International Journal of Applied Mathematics and Statistics, 2013, 51(22):196-204.

[5] GUO Youlin, ZHAO Minghua, DENG Zongwei. Tunnel surrounding rock deformation forecast analysis based onGM and FEM[J]. Electronic Journal of Geotechnical Engineering, 2014, 19:1379-1394.

[6] 高宁，崔希民，高彩云.高层建筑物沉降变形的灰线性预测[J].测绘科学,2012,37(3):96-98.

[7] Matin T.Hagan,Howard B.Demuth,Mark H.Beale.神经网络设计[M].鱿葵.北京.机械工业出版社,2002.

[8] 周毅,罗郧,贾三满,等.灰色线性回归组合模型在北京地面沉降分层预测中的应用[J].城市地质,2014 (4) :52-56.

[9] 张俊中,雷伟伟，王睿，等.灰线性回归模型在建筑物沉降分析中的应用[J].河南科学,2015,33(3):416-420.

[10] 李克昭,李志伟,赵磊杰.灰线性马尔科夫模型在建筑物变形监测中的应用[J].测绘工程,2016,25(10):5-9.

[11] 马天驰.基于灰色 RBF 神经网络模型在建筑物沉降预测中的应用[J]. 黑龙江工程学院学报, 2016, 30(2):5-7.

[12] 黄禄文,刘海卿.建筑物基础沉降径向基神经网络预测[J] .辽宁工程技术大学学报(自然科学版),2016,35(8):836-840.

[13] 崔一,杨勇辉.基于改进RBF 神经网络的巷道变形预测模型[J].金属矿山,2016(8):170-173.

[14] 赵福洪，罗志清，杨建文.七种数学模型在沉降预测中的优缺点比较分析[J].测绘工程，2014，23(3)：59-62.

[15] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础武汉大学出版社[M].武汉:武汉大学出版社，2014.

PredictionModellingofOptimizedGray-linearRegressionModelBasedonRBFNeuralNetwork

ZHAO Ya-hong，HAO Yan-jin, DING Jian-chuang

(SchoolofArchitecturalEngineering,NorthChinaInstituteofScienceandTechnology,Yanjiao, 065201,China)

According to the characteristics of the mechanism of foundation settlement and RBF neural network, which can effectively describe the uncertainty problem and solve the complex nonlinear problem, an optimized gray-linear regression prediction model based on RBF neural network was established. Through the engineering data, the prediction accuracy of single gray model, gray-linear regression model and optimized gray-linear model based on RBF were analyzed. The results showed that the fitting and forecasting accuracy of the optimized gray-linear prediction model based on RBF was better than gray model and gray-linear regression model, and the mean square error was 0.0014mm. The optimized gray linear model can well reflect the general trend and regularity of building settlement.

RBF; optimization; gray-linear regression model; settlement prediction

2017-07-19

廊坊市科技支撑计划(2016011014)

赵亚红(1982-)，女，河北衡水人，硕士，华北科技学院建筑工程学院讲师，研究方向：工程测量。E-mail：neu_zyh@163.com

TP183

A

1672-7169(2017)04-0103-04