软土地区地铁矩形隧道长期沉降规律及预测

张学华， 王怀东

(1. 南京地铁运营有限责任公司， 南京 210037； 2. 中铁隧道勘测设计院有限公司， 天津 300133)

软土地区地铁矩形隧道长期沉降规律及预测

张学华1， 王怀东2

(1. 南京地铁运营有限责任公司， 南京 210037； 2. 中铁隧道勘测设计院有限公司， 天津 300133)

针对运营中的软土地区某地铁区间矩形隧道的病害发展情况，从大量监测数据入手，分析研究隧道变形发展在各个时期的规律(结构自身应力平衡、土层固结、周边环境变化)，发现该区域隧道变形主要受软弱地质条件及周边物业开发影响。同时，针对计算结果，分析该隧道各个区段沉降发展趋势，认为在无外部影响情况下，隧道沉降呈收敛趋势。为该隧道的沉降治理提供有效的理论依据，也为类似工程提供参考。

轨道交通； 软土地区； 矩形隧道； 沉降规律； 沉降预测

1 研究背景

随着城市轨道交通的快速发展，大量地铁运营线路位于以饱和淤泥质黏土、软流塑粉质黏土等以高压缩性长江漫滩软土为主的地区，且同类地区仍有较多的地铁线路规划建设。如果高压缩性软土地区的地铁隧道基础处理不当，经长期运营后，在列车荷载作用、周边地块开挖降水影响下，极易引发隧道不均匀沉降，造成结构开裂、渗漏、道床错台及翻浆冒泥、轨面不平顺、接触网净空不够等病害[1]。理论上，可以通过日常监测所得数据分析得出隧道变形规律及病害发展，预先进行病害治理，做到“预防为主，防治结合”。但由于在软土地区中，隧道变形受外界影响较大，变形规律及病害发展不宜控制，使得判断准确性降低，实际预防效果不显著，病害产生后才治理[2]。因此，对软土地区地铁隧道长期沉降规律的分析及预测具有非常重要的现实和指导意义。

本文基于软土地区某地铁矩形隧道区间，分析研究了矩形隧道在软土地区沉降变形的原因、隧道自身变形发展规律及对未来隧道变形规律的预测，为今后预防和治理提供有效的理论依据。

2 工程概况

所研究地铁矩形隧道工程主要穿越淤泥质粉质黏土、粉土层，局部穿越粉细砂层，隧道下卧土层主要为淤泥质粉质黏土和粉细砂层。区间隧道部分区域基底加固采用抽条加固。如图1所示。

图1 矩形隧道围护横断面Fig.1 Cross section of rectangular tunnel

3 沉降规律

3.1隧道沉降及病害表现

现该项目投入运营10余年，在运营初期开始设置基标对全段隧道进行沉降监测，测点间距约20～50m，后期在沉降量较大的区间按照5m间距加密，监测周期为3个月，至2015年底已完成56期的沉降监测数据。

运营至今，根据第56期的沉降监测数据结果显示，区间已经出现较大的不均匀沉降，最大累计沉降达300.02 mm，并形成5个较明显的沉降槽。同时，区间结构也出现各种不同程度的病害，主要体现在：框架结构裂缝、框架结构渗漏水、道床翻浆冒泥等。见图2。

图2 矩形区间隧道病害表现Fig.2 Disease representation of rectangular tunnel

裂缝总体的发展方向是由下部向顶部发展。裂缝分布于整个隧道区间内，间距为0.3～8 m不等，宽度普遍在0.1～0.3 mm之间。

渗漏水出现的部位也包含了所有裂缝涉及到的部位，如拱顶、边墙、道床以及水沟。从现场情况来看，渗漏主要为裂缝处的慢渗，局部有快渗现象。

隧道内混凝土整体道床不仅有横向裂缝，还存在着较多的纵向道床与边墙的剥离缝，并长期伴有较多的翻浆、冒泥、渗漏水现象，部分区段水质腐臭发黑，并伴有气泡，水沟内亦有较多细砂和粉质淤泥状物质沉淀。

对于以上病害，如不加以治理，势必影响地铁的运营安全。但如何治理，是小成本例行维修还是大预算结构加固是一个难以抉择的问题。因此解决该问题最直接的方法是论证各项病害对隧道结构安全是否有影响，并预测不均匀沉降是否会进一步发展，从根本上分析判断隧道结构的安全性。

对于该问题， 2004—2007年先后召开了多次专家会议，论证地铁运营安全及治理措施，并多次对病害进行了治理。但随着时间的推移，区间隧道沉降一直在持续，并有多个区域形成了较大的沉降槽，相应的病害也应运而生，问题不断，这主要是因为没有结合地铁区间本身及分析周围环境问题导致。

3.2隧道沉降发展与地质的相互关系

从图3地铁区间相对运营初值的累计沉降量变化曲线图可以看出：车站沉降量相对较小，区间沉降量较大；沿线范围内形成了5个明显的沉降槽(B1～B5)，沉降槽在形成时间上有所差异，且沉降槽有向两边扩展的趋势。沉降槽均处于②-2b4淤泥质粉质黏土(流塑)地层中，沉降量较大。如图3、4所示。

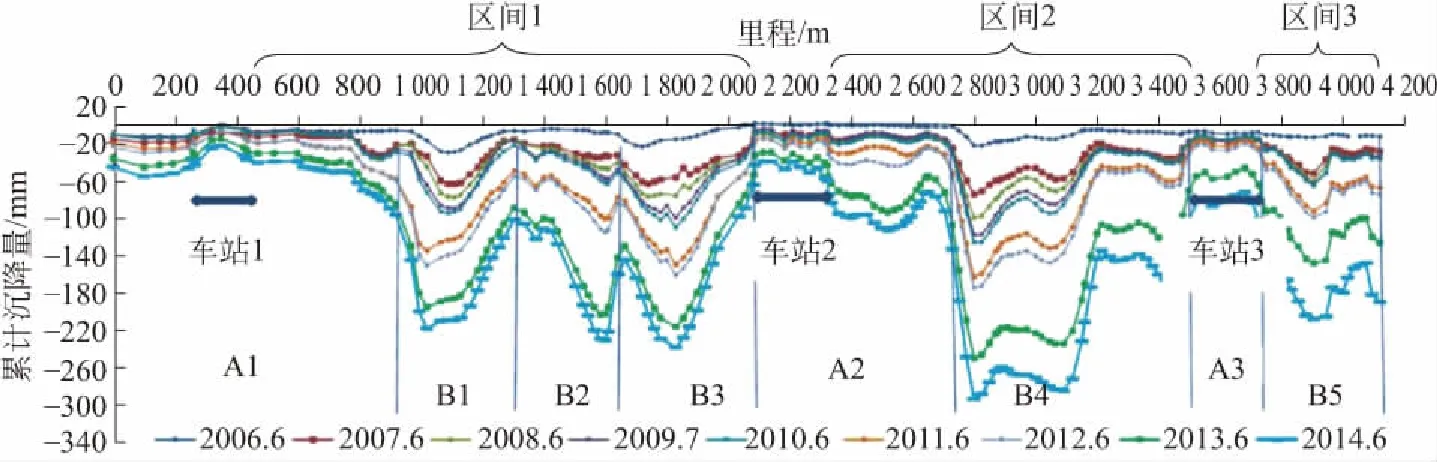
图3 地铁区间累计沉降量变化曲线Fig.3 The chart of the change curve by accumulated settlement

图4 地铁区间累计沉降量变化曲线对应地质图Fig.4 The chart of the geology which corresponds with the change curve by accumulated settlement

3.3隧道沉降发展与周边物业开发的对应关系

该工程自建成投入运营以来，线路两侧的建筑活动频繁开展，大多为深基坑的商业及居住项目。本工程沉降槽与周边建筑物的对应关系纵断面见图5。

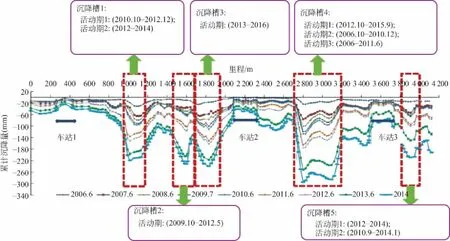
图5 区间隧道现状沉降槽分布与周边地块开发建设纵断面关系Fig.5 The relationship between the distribution of the interval tunnel and the development and construction of the vertical section of the surrounding block

由于区间隧道周边物业开发数量较多、规模较大，且多为深、大基坑，与隧道外边缘间距最小的仅为2m。在其基坑施工时间内，临近的区间隧道出现了较为明显的沉降槽，且沉降量较大。由此可判断，区间隧道除了因地层产生的沉降变形外，周边物业开发对其影响较大。现今，对于地铁保护要求，各个城市均有不同的标准，但大多数为15～25m。根据本工程所得数据，认为可根据确切地层制定相对应的地铁保护要求，扩大地铁保护范围。

通过监测数据发现，沉降槽在工程结束后并未停止变形，而是一直保持缓慢变形的状态，即沉降量一直在增大。普通维护只能采取堵漏、调校导高等措施，而不能解决隧道沉降的问题，同时随着隧道持续变形，会继续出现裂缝、渗漏等病害，增加维修成本。

此时，需对区间隧道病害进行进一步分析，判断隧道沉降的发展规律及趋势，在未进行加固措施时隧道自身是否趋缓，为治理方案提供依据。

4 沉降预测方法及结果

通过对大量文献及工程实例的研究[3-5]可以明确，当区间隧道的沉降发展到一定程度以后，势必会呈现出不同的发展趋势，或继续发展，或逐渐收敛。

国内外对沉降预测方法的研究已有了多元化的发展[6-8]，其中曲线拟合法可通过实测数据得到隧道沉降发展的规律，并通过该规律预测隧道沉降发展的趋势，这一方法在实际工程中应用较广，且研究成果较多。

监测数据通常表现为离散性较高的非线性曲线，在进行样本分析时需对监测数据进行筛选整合，并保证曲线拟合的逼近函数与监测数据的样本区间尽可能多地重合。其中，最小二乘法是曲线拟合计算最常用的一种具体方法。

由于非多项式曲线可以通过变数变换将其化为多项式曲线拟合，这里着重介绍多项式曲线拟合过程。

假设两个变量函数关系为y=f(x,b0,b1,b2,…,bn)，若拟合模型f(x,b0,b1,b2，…，bn)=b0+b1x+b2x2，…，+bnxn，则称其为多项式拟合，这里的1+n个参数(b0,b1,b2，…，bn)对应着需要1+n组监测数据yi=f(xi,b0,b1,b2，…，bn)来确定，通常采用参数(b0,b1,b2，…，bn)，使得f(x,b0,b1,b2，…，bn)在x1,x2，…，xn处的函数值与监测数据y1,y2，…，yn的偏差的平方和为最小，使得

(1)

为最小，通过对参数取偏导求极值，即

(2)

得到线性方程组

(3)

利用矩阵计算求出(b0,b1,b2,…,bn)，代入y=f(x,b0,b1,b2,…,bn)，得到其拟合曲线的函数模型，进而计算出所需要的预测值。

南京河西地区与上海地区均为高压缩性土层，可引用上海地区的经验公式[9]，即双曲线公式为

(4)

式中，Smax为隧道在不采取任何措施情况下的最终沉降量；α为计算系数；t为沉降至St的时间。

通过上述式(1)～(3)，求解出Smax、α，然后根据相应计算里程点的监测资料，将参数Smax、α，时间及沉降值代入式(4)，即可求出任意里程点需要预测的任意时刻的沉降值St。

同时，考虑到实际隧道沉降的曲线较为复杂，部分曲线段采用对数函数进行拟合[10]，有

St=Smax(a0+a1lnt)

(6)

采用相同方法,根据监测数据求出任意里程点需要预测的任意时刻的沉降值St。在对比双曲线公式和对数函数公式时，取拟合程度较高的作为拟合曲线。

通过上述对监测的数据分析，得出由于隧道周边物业开发活动频繁，隧道的沉降曲线经历了多次增大—收敛的发展过程，由此可知，沉降曲线拟合的函数应为一个分段函数，且各个时间段对应不同的分段函数。如图6可知，隧道沉降值随着时间的推移，累计沉降量虽有增大，但整体曲线符合收敛趋势，整体沉降值对应函数曲线拟合率较高。因此，只能根据近期数据未发生突变的曲线段来拟合，从而预测隧道长期的沉降数据。

图6 沉降值与时间对应关系曲线Fig.6 Relationship between settlement and time

根据以上理论分析，选取区间1特征点L029(见表1)，采用对数函数模型进行拟合预测分析，并对所选拟合模型进行反推，观察与现有监测值的相关性。

根据对数函数计算模型和L029的监测数据，推算出沉降曲线为：

y=-12.62ln(x)-23.953

(7)

式中，x为根据监测频率确定时间间隔系数；y为对应时间段的沉降值。

根据以上公式所得如表1、图7所示。预测曲线较为圆滑，监测值曲线相对离散，但两者曲线趋势都明显趋于平缓，且分布点的值也基本相近，数值相关性可达到0.98。

表1 特征点L029预测值与监测数值对比

基于以上分析,从5个典型沉降槽上选取特征点,得到相应的时间和沉降值,通过上述公式对长期沉降值进行求解,其结果如表2、3,图8、9所示。从表2、表3可知,通过对沉降速率有规律的监测数据对比分析可知,隧道在地铁运营过程中仍存在沉降,最大沉降量为238.22mm,为L200号监测点,但沉降速率有所减小,整体上沉降曲线趋于平缓。

从图8、9可知,对区间1沉降趋势采用对数函数模型进行预测,所得出的结果显示,沉降延续近两年所得监测数据结果的沉降趋势,沉降量仍然有所增大，而沉降速率继续减小。当预测时间为2020年7月，沉降量最大的点L155沉降值将达到294.49 mm，相比最后一期监测数据，增大64.58 mm，沉降速率为0.032 mm/d；当预测时间为2035年7月份，沉降量最大的点L155沉降值将达到347.4 mm，相比最后一期监测数据，增大117.5 mm，沉降速率为0.016 mm/d；由两次沉降速率相比可知，随着时间的增加，沉降速率继续减小，沉降槽成收敛趋势。

表3 区间1特征点沉降值预测

图8 区间1特征点沉降值预测Fig.8 The chart of the prediction of sedimentation value by 1st interval tunnel

图9 区间1沉降趋势预测Fig.9 The chart of the prediction of settlement by 1st interval tunnel

采用相同方式分别对区间2、3的沉降槽进行预测，如表4、5，图10～13所示。

表4 区间2特征点沉降值预测

表5 区间3特征点沉降值预测

图10 区间2特征点沉降值预测Fig.10 The chart of the prediction of sedimentation value by 2nd interval tunnel

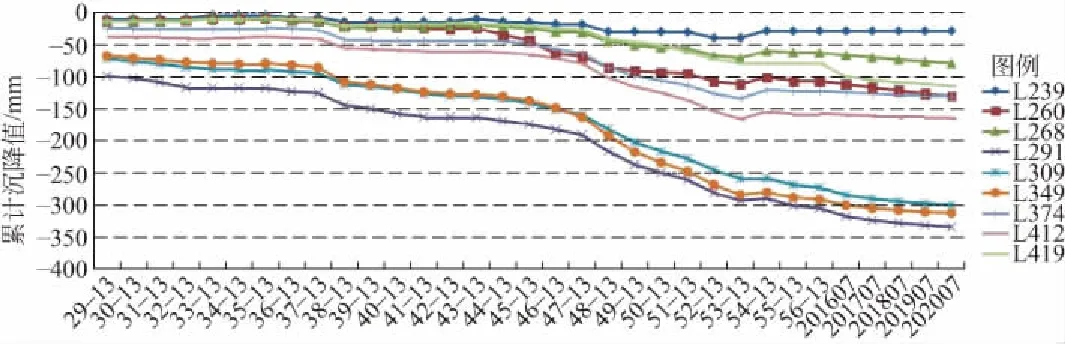
图11 区间2沉降趋势预测Fig.11 The chart of the prediction of settlement by 2nd interval tunnel

图12 区间3特征点沉降值预测Fig.12 The chart of the prediction of sedimentation value by 3rd interval tunnel

图13 区间3沉降趋势预测Fig.13 The chart of the prediction of settlement by 3rd interval tunnel

从图10～13可知，区间2、3的沉降槽随着时间的推移，沉降量均有所增大，但整体沉降速率减小，沉降曲线趋于收敛。

根据以上沉降预测值，选取区间1特征点以57-13期(201601)和58-13期(201604)的监测数据与预测值进行对比，详见表6所示。

表6 区间1沉降值与预测值对比

根据表6可知，预测值为2016年7月，而监测数据最近的为2016年4月，从表中可知，57-13期与58-13期的沉降差较小，沉降速率较小。而58-13期与预测值基本相近，个别点相差约2.2 mm，但整体数据基本相似。

同时，根据现阶段拥有的监测数据，分别对各个地铁区间运营100年时的沉降值进行预测，如图8～13所示。从图中可知，各个沉降槽在运营100年时沉降量增量较2035年小，整体趋近平缓，这与土体在自然固结状态下达到地应力平衡后地层基本不变相吻合，说明本次预测分析符合土体固结规律。

从以上结果可以得出：1) 采用双曲线及对数函数对实际监测数据进行拟合预测，其相关性系数较好(约0.98)，适用于本项目隧道的长期沉降预测；2) 区间隧道随着时间的推移，虽沉降速率减小，但总沉降量会继续增大，应加强隧道监测并对隧道采取相关治理措施；3) 本次预测计算并未考虑周边物业开发等对地层扰动的工程建设，需结合实际土层扩大地铁保护范围，严格要求工程建设相关标准。

5 结论

本文对地铁区间沉降数据分析及沉降预测方法进行探讨，同时也对预测结果进行分析，总结出以下几点：

1) 在压缩性较大的软弱地区，隧道变形受土层性质和周边物业开发的影响较大，在基坑施工过程中，应采用满堂加固的方式进行基底加固；同时应严格控制周边物业开发，必要时采取加固或隔离措施降低物业开发对区间隧道的影响。

2) 在运营期间，对区间隧道进行维护保养时，应结合监测数据，分析判断隧道沉降是否趋缓，否则需采用必要的加固措施。

3) 本文采用双曲线公式和对数函数对已有监测数据进行曲线拟合，拟合所得公式与原有监测数据相关性较好，预测所得值符合地层变形的规律，可以作为沉降治理的一个参考。

[1] 李桂华，黄腾.软土地铁隧道运营期沉降监控研究综述[J].南京:河海大学学报(自然科学版),2011，39(3)：277-284.

LI Guihua, HUANG Teng. Review on settlement monitoring of metro tunnel in soft soil[J]. Journal of Hohai University(natural sciences), 2011, 39(3): 277-284.

[2] 黄腾，孙景领.地铁隧道结构沉降监测及分析[J].东南大学学报(自然科学版),2006,36(2):262-266.

HUANG Teng, SUN Jingling. Subsidence monitoring and analyzing in subway tunnel construction[N]. Journal of Southeast University(natural sciences edition), 2006, 36(2): 263-266.

[3] 杨兵明.软土地层盾构隧道长期沉降规律及预测研究[J].铁道工程学报,2015，32(11)：87-92.

YANG Bingming. Research on the law and prediction of Long-term settlement of shield tunnel in soft soil stratum[J]. Journal of railway engineering society, 2015, 32(11): 87-92.

[4] 姜洲，高广运.软土地区地铁行车荷载引起的隧道长期沉降分析[J].岩土工程学报,2013,35(2):301-307.

JIANG Zhou, GAO Guangyun. Long-term settlement of tunnels induced by subway moving load in soft soil districts[J]. Chinese journal of geotechnical engineering, 2013, 35(2): 301-307.

[5] 赖金星，樊浩博.软弱黄土隧道变形规律现场测试及分析[J].岩土力学,2015，36(7)：2003-2012.

LAI Jinxing, FAN Haobo. In-site monitoring and analysis of tunnel deformation law in weak loess[J]. Rock and soil mechanics, 2015, 36(7): 2003-2012.

[6] 刘峰.软土地区地铁隧道长期沉降及对地铁安全的影响[D].南京:南京大学,2013.

FENG Kai. Longterm settlement of metro in soft ground and its influence on safety[D].Nanjing： Nanjing University, 2013.

[7] 韦凯，宫全美，周顺华.软土盾构隧道不均匀沉降预测的蚁群算法改进及参数选取[D].岩石力学与工程学报，2011，30(1):3022-3031.

WEI Kai, GONG Quanmei, ZHOU Shunhua. Improvement of antcolony algorithm for predicting uneven settlements of shield tunnel in soft soil and its parameters selection[N]. Chinese journal of rock mechanics and engineering, 2011, 30(1): 3022-3031.

[8] 赵春彦,周顺华,袁建议.地铁荷载作用下叠交隧道长期沉降的半解析法[J].铁道工程学报,2010，32(4)：141-145.

ZHAO Chunyan, ZHOU Shunhua, YUAN Jianyi. Semianalytical soloution for long-term settlement of overlapped tunnel under subway loading[J]. Journal of the china rail way society, 2010, 32(4): 141-145.

[9] 张震.盾构隧道结构长期沉降研究综述[J].应用技术,2013(3):134-140.

ZHANG Zhen. On the Long-term settlement of shield tunnel structure[J]. Applied technology, 2013(3): 134-140.

[10] 韦凯，宫全美，周顺华.隧道长期不均匀沉降预测的蚁群算法[J].同济大学学报(自然科学版)，2009，37(8):994-998.

WEI Kai, GONG Quanmei. Ant colony algorithms of long-term uneven settlement prediction in tunnel[J]. Journal of Tongji University(natural science), 2009, 37(8): 994-998.

Long-term Settlement and Predictive Analysis of Rectangular Subway Tunnels in Soft Soil Areas

ZHANG Xuehua1, WANG Huaidong2

(1. Nanjing Metro Operation Co., Ltd., Nanjing 210000; 2. China Railway Tunnel Survey & Design Institute, Co., Ltd., Tianjin 300133)

The development law of tunnel deformation in various periods are explored in terms of self-stress equilibrium of the structure, the liquefiable soil and changes in the surrounding environments, by using the monitoring data of the disease changes of the in-service rectangular tunnel located in soft soil areas. It is found that the problem of tunnel diseases was mainly influenced by weak geological conditions and the surrounding property development in the area. At the same time, the development of deformation in each section of the tunnel is analyzed on the basis of the calculation results. Under the condition of no external influence, the settlement of the tunnel is convergent, which provides effective theoretical basis for the settlement of the tunnel, and also presents references for similar projects.

urban rail transit; soft soil districts; rectangular tunnel; law of settlement; prediction of settlement

10.3969/j.issn.1672-6073.2017.05.013

2016-11-15

2016-12-08

张学华，男，本科，高级工程师，工程部部长，主要研究方向为轨道交通运营维修保养，2638488669@qq.com

U231

A

1672-6073(2017)05-0070-08

(编辑：郝京红)