赤道海洋Kelvin波对外强迫风场的响应
2017-11-13陈光泽卢姁张铭
陈光泽,卢姁,张铭
(1.解放军61428部队,北京 100072;2.解放军61741部队,北京100094;3.解放军理工大学气象海洋学院大气环流与短期气候预测实验室,江苏南京 211101)
赤道海洋Kelvin波对外强迫风场的响应
陈光泽1,卢姁2,3,张铭3
(1.解放军61428部队,北京 100072;2.解放军61741部队,北京100094;3.解放军理工大学气象海洋学院大气环流与短期气候预测实验室,江苏南京 211101)
采用无界理想海洋线性扰动模型,对赤道海洋Kelvin波在纬向风场异常强迫下的响应即强迫赤道海洋Kelvin波的异常做了解析求解,主要结果如下:该强迫赤道海洋Kelvin波的频率、波长和波速都与外强迫风场的相同,在赤道纬向流振幅最大并随纬度增加衰减,该风场越强,该强迫赤道海洋Kelvin波也越强,两者呈正比关系。当该风场频率和范围确定后,则该强迫赤道海洋Kelvin波被限制在一定平均水深范围内;该风场的频率越高、纬向波长越长、随纬度增加衰减越小,则该水深就越大。在所取参数下,该风场异常与该强迫赤道海洋Kelvin波流场异常的位相基本相同。在西风强迫下有东向流,反之亦然;强迫赤道海洋Kelvin波的流场与位势场则完全同位相,东向流对应于正位势,反之亦然,这也是经典Kelvin波的配置。该强迫赤道海洋Kelvin波与经典Kelvin波的不同在于:前者是频散的强迫波动,并被限制在一定水深中;后者是自由波动。将该强迫Kelvin波的解析解与热带印度洋和太平洋的实况以及诊断进行对比后知,两者总体看来一致,实际热带大洋中该强迫赤道海洋Kelvin波应确实存在。
热带大洋;Kelvin波;强迫风场;响应;解析解
1 引言
热带虽因Coriolis参数f趋于零,但其导数β=df/dy却在赤道上最大,从而使得热带运动具有特色。在热带,向东传播的有Kelvin波,向西传播的有Rossby波,此外还有高频的惯性重力波,以及向西传播的混合Rossby重力波,这些即为Matsuno波系[1],即赤道波系。该波系中的Kelvin波在大气和海洋中都具有向东传播,其流场仅为纬向流动,波振幅在赤道上最大,并随纬度增加呈指数平方衰减的特点[1]。
因海洋赤道波系中Kelvin波和Rossby波的调节,会产生年际尺度的振荡,并能够解释ENSO循环[2-3],故赤道海洋Kelvin波一直受到研究气候变化学者的关注。Hirst[4]和Yamagata等[5]从理论上证明了热带海气耦合系统中也存在向东传播的扰动,并认为这是因东传的赤道海洋Kelvin波所引起的。Zheng等[6]指出,赤道太平洋次表层暖水的快速东传使得热带中东太平洋海表温度未来明显增暖,造成厄尔尼诺事件爆发,而这与赤道海洋Kelvin波的东传密切有关。张东凌等[7]、卢姁等[8]对大气风场和海洋流场异常的联合复EOF分解结果表明,热带太平洋和热带印度洋都存在这样的现象:该分解的主要模态为赤道所俘获,仅表现为纬向流动的形态,这与赤道海洋Kelvin波的形态很相似。
在热带赤道地区多盛行纬向风,在纬向风强迫下,海洋上层的赤道Kelvin波必然会做出响应,并由自由赤道Kelvin波转变为强迫赤道Kelvin波。强迫赤道海洋Kelvin波具有何种表现形式?其与自由赤道海洋Kelvin波的性质有何异同?其与外强迫纬向风场有何联系?这些均是令人感兴趣的重要问题。这些问题的解决,有助于揭示强迫赤道海洋Kelvin波的动力机制以及海气耦合过程。解析研究能够直观地给出各物理量之间的定量联系并得到各种规律的数学表达式,这是诊断分析和数值实验难以做到的。前人有关赤道海洋Kelvin波的研究工作虽有不少[9-10],也涉及到风场对赤道海洋Kelvin波的强迫[11],但是关于强迫赤道海洋Kelvin波的解析研究则尚不多见。给出一个简化的理想海洋模型,在一定条件下,求得该模型中赤道海洋Kelvin波对外强迫风场响应的解析解,即强迫赤道海洋Kelvin波的异常,则是回答以上问题的途径之一。为此本文做了这方面的工作,并对求得的解析解做了分析讨论,试图回答上述问题。
2 数学模型和求解
考虑一个两层正压无界海洋系统,上层为受风应力驱动的风生流,下层为静止,在赤道地区,对于上层则有以下赤道β平面线性化扰动的正压原始方程组[12]:
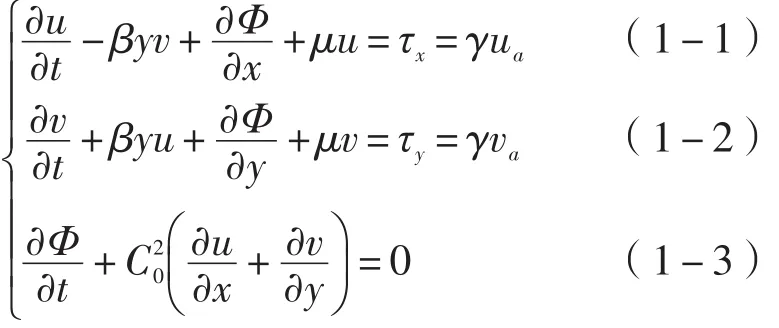
在此,不考虑背景流,但考虑了大气风应力对海洋的强迫和瑞利摩擦[13]。在方程组(1)中,τx=γua、τy=γva为外强迫风应力异常的两个分量,ua、va为外强迫风场异常的两个分量;γ为比例系数,μ为瑞利摩擦系数,两者均设为常数[13];β=(∂f ∂y)y=0,即 β 取赤道上的值;=g′Hˉ,Hˉ为上层的平均水深,即风应力异常驱动海水扰动的平均深度,在该平均深度以下流动为静止;g′=(ρ2-ρ1)·g ρ2是约化重力加速度,g 为重力加速度,ρ1、ρ2分别为上层和下层的海水密度,都设为常数[14];u,v为海洋流场扰动的两个分量,Φ为海洋位势场的扰动。在此外强迫风场以及海洋的流场和位势场均为扰动,即异常;以下为方便,在不会混淆时则略去“扰动”和“异常”的称谓。
在赤道地区盛行纬向风,故本文仅考虑纬向风的强迫。为便于求取方程组(1)的解析解而又与实际情况大致吻合,则取外强迫风场为以下波动形式:
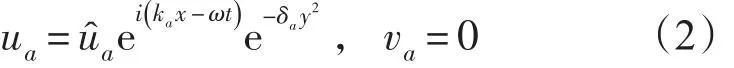
式中:ua、δa、ka和 ω均为大于0的实常数,分别为该风场的振幅、该风场振幅随纬度增加的衰减系数、该风场在纬向(x方向)的波数和频率;ca=ω ka>0为该风场向东传播的相速。在该模型中记某时某地为t=0,x=0,则此时此地则为西风强迫。因式(1)为线性方程组,叠加原理成立,该风场的演变可表示为各种振荡频率的叠加,故只须求解对某一频率ω的特解即可。
为求此时赤道海洋Kelvin波对频率为ω的风场强迫响应,即求取强迫赤道海洋Kelvin波的特解,可设v≡0。再设波解:
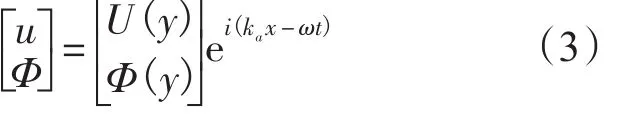
式中:认为强迫赤道海洋Kelvin波的频率也为ω,波数则为ka,它们与上面外强迫风场的相同。将式(3)代入式(1)后则有:
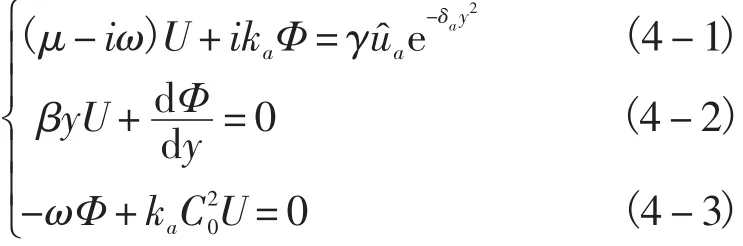
现再设该强迫赤道海洋Kelvin波振幅随纬度增加的衰减与外强迫风场的相同,两者衰减系数都为 δa,这样有:

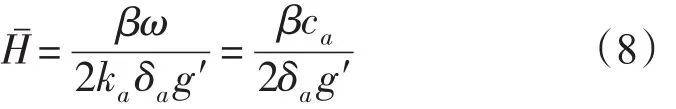
式(8)表明,当外强迫风场频率、波数和衰减系数确定后,即ω、ka和δa确定后,则此时强迫赤道海洋Kelvin波对外强迫风场的响应就被限制在平均水深Hˉ上,在Hˉ以下流动为静止,Hˉ也是强迫赤道海洋Kelvin波的平均厚度;外强迫风场的频率ω越高、纬向波长越大(波数ka越小)、衰减系数δa越小,则强迫赤道海洋Kelvin波的平均厚度Hˉ就越大。
将式(6-1)与式(6-2)联立,则可求得复常数u和Φ :
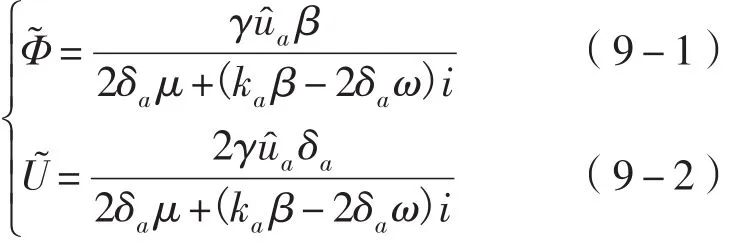
最后可得该赤道海洋Kelvin波对外强迫风场的响应,即方程组(1)的强迫赤道海洋Kelvin波特解的解析表达式:
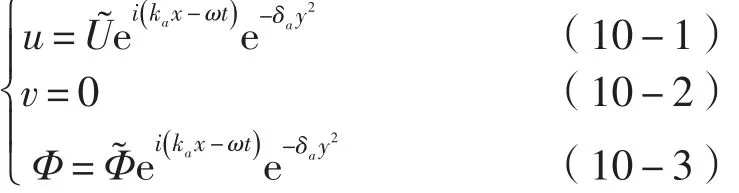
ф 、u的表达式见(9-1)、(9-2)式。该解用复数表示,有物理意义的部分是其实部。
由式(10)可见:赤道海洋Kelvin波对外强迫风场的响应即强迫赤道海洋Kelvin波振幅在赤道最大,并随纬度增加衰减。强迫赤道海洋Kelvin波的频率、波长、波速和振幅随纬度增加的衰减(衰减系数)都与外强迫风场的相同。当外强迫风场的频率和范围确定后,强迫赤道海洋Kelvin波的响应被限制在一定的水深范围以内。强迫风场越强,则强迫Kelvin波也越强,两者呈正比关系。
3 计算结果分析
3.1 季节变化
一年四季的季节变化是最基本的气候变化。通过选取各参数典型值的计算,可得到海洋赤道Kelvin波对外强迫纬向风场季节变化响应的具体情况。为考察该风场的季节变化,取其周期T=1 a,这时有ω=1.991×10-7/s。因风速典型值为10 m/s,本文取其20%作为风场异常值,即取ua=2 m/s。现取γ=1×10-6[13],μ=3×10-5[13],还取 δa=2×10-11/m2;取系数(ρ2-ρ1)/ρ2为1.704×10-5,重力加速度 g=9.8 m/s2,这种情况下约化重力加速度为g′=1.67×10-4m/s2,β则取赤道上的值,为2.289/(m·s)。取纬向风异常的纬向波长L=2 500 km,此时相应有ka=2.513 3×10-6/m,ca=ω/ka=7.922×10-2m s。这样在赤道上最大的风场、流场和位势场分别为而由(8)式知 Hˉ=271.5 m,该强迫赤道海洋Kelvin波已到达海洋次表层。
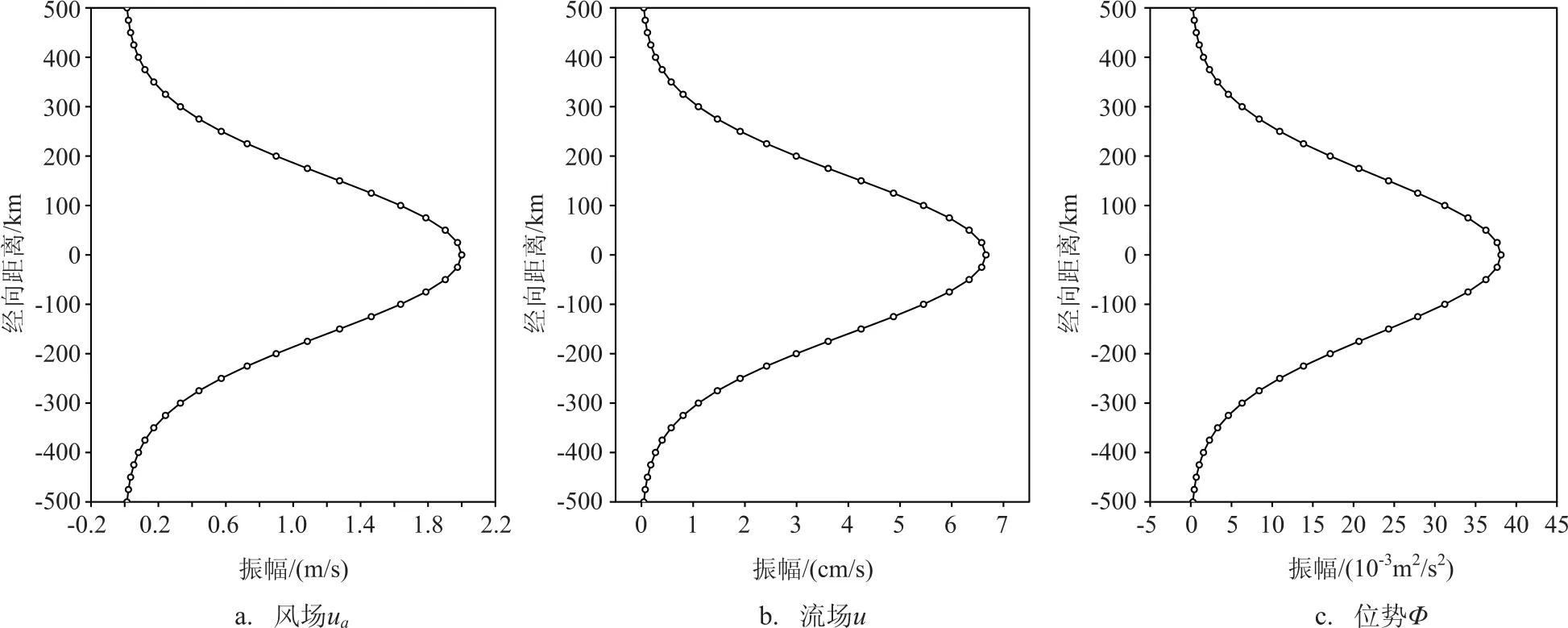
图1 各场振幅的经向分布(纵坐标0处为赤道)
图1 给出风场,该强迫赤道海洋Kelvin波流场和位势场在各经度上的振幅分布。风场振幅最大值出现在赤道,为2 m/s,并随纬度增加很快衰减(见图1a)。该强迫赤道海洋Kelvin波流场和位势场的振幅与风场一样,振幅最大值也出现在赤道上,其值分别为6.66 cm/s和38.12×10-3m2/s2,并随与赤道距离的增加而很快衰减(见图1b、c)。
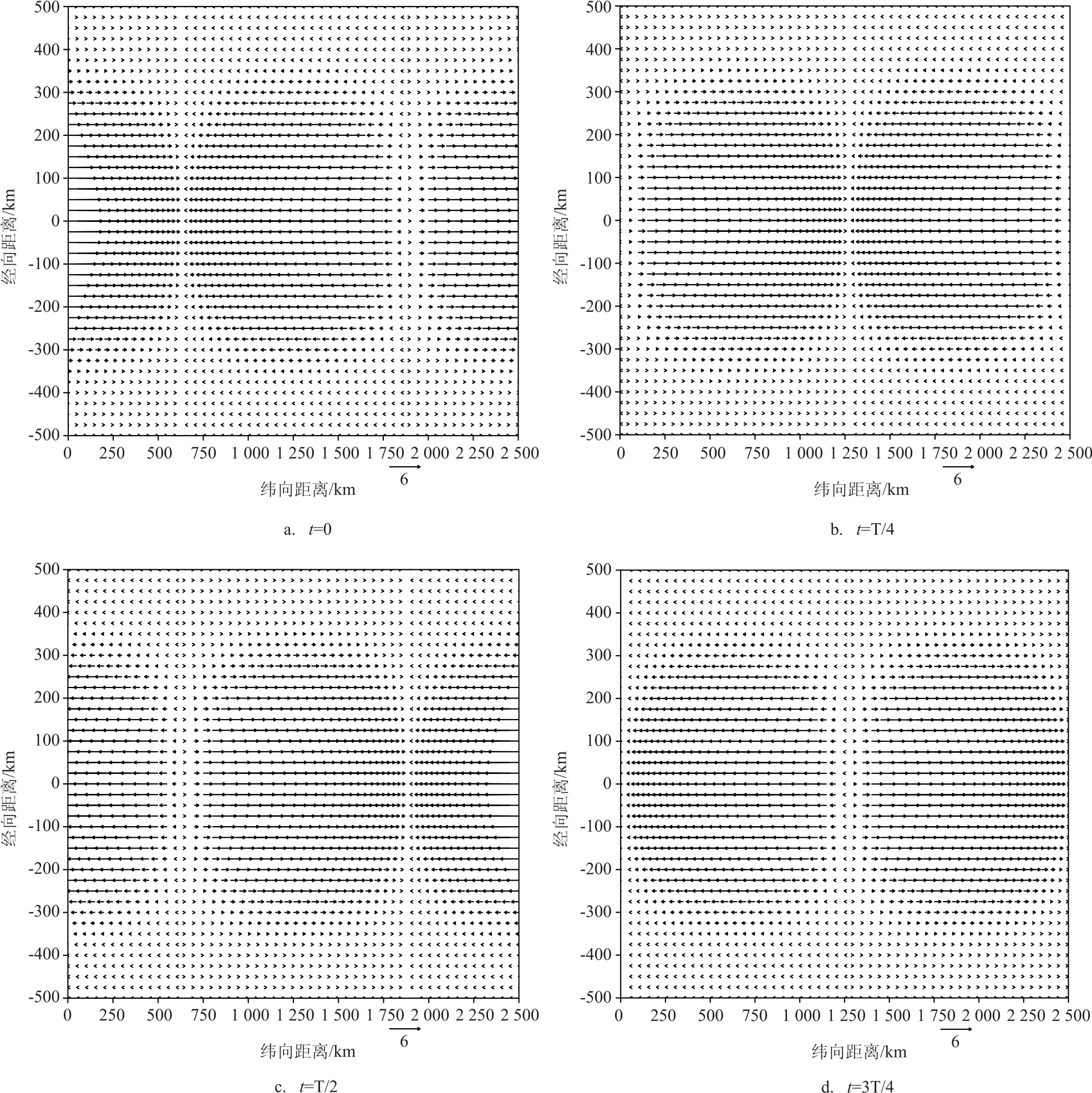
图2 各时刻流场的水平分布(周期T=1 a,纵坐标0处为赤道,图中箭矢单位:cm/s)
图2 给出了以赤道为中心,南北各取500 km计算得到的强迫赤道海洋Kelvin波流场。t=0时(见图2a),因外强迫风场的波长为2 500 km,故赤道海洋Kelvin波受到该风场强迫,在0~600 km有东向流;在650~1 850 km有西向流;在1 900~2 500 km又为东向流;该东、西向流的极值都出现在赤道上,为6.66 cm/s(见图1b),且该流场响应随与赤道距离的增加而很快衰减。当t=T 4时(见图2b),则随着该风场的东传,该强迫赤道海洋Kelvin波的流场也相应东传,东向流与西向流的交界已东移至1 250 km处。当t=T 2时(见图2c),该流场随该风场继续东传,此时该流场与t=0时恰好反位相。当t=3T 4时(见图2d),该流场仍有规律东传,此时该流场与t=T 4时也恰好反位相。当经过1个周期T即1a后,强迫赤道海洋Kelvin波的流场形态又回到t=0时(见图2a),完成了周期为1a的循环。
图3 给出了t=0时外强迫风场、强迫赤道海洋Kelvin波的流场和位势场的水平分布,图的范围同图2。该风场、流场和位势场的最大绝对值都出现在赤道上,随着与赤道距离的增加而迅速衰减。风场与流场两者位相相差不大。在东风强迫区,则有西向流,反之亦然(见图3a、b)。而流场与位势场两者则完全同位相(见图3b、c),流场的东向流对应于正位势,反之亦然,这也是正压赤道Kelvin波的特点[1,15]。为方便以下称该正压赤道Kelvin波为经典Kelvin波,Matsuno[1]首先对其做了研究。在其他时次,它们与图2相对应,均有规律的东传,1a后完成一个周期循环。
图4给出了赤道上x=0处外强迫风场以及强迫赤道海洋Kelvin波流场和位势场随时间的变化。赤道附近风场异常ua的极值为2 m/s,随时间呈余弦函数振荡(见图4a);强迫赤道海洋Kelvin波流场和位势场均与该风场有很好对应关系,流场与风场基本呈同位相变化,而位势场与流场则完全呈同位相变化。
3.2 年际变化
因ENSO有3—7a的年际变化,故考虑外强迫风场的年际变化也是很有意义的。在此风场的年际变化周期取为3—7a之间的4a即T=4a,则有ω=4.977 6×10-8/s。此外其他参数取得均与节3.1相同,不再赘述。由这些参数可得到,在赤道上最大的风场、流场和位势场分别为ua=2 m s,这些与节3.1中相应的值几无差别;然而在此有Hˉ=67.87 m,这与节3.1中的相应值差异较大,年际变化下强迫赤道海洋Kelvin波对风场响应的深度远较节3.1季节变化下的要浅,风场对海洋的影响集中在海洋表层。
因该情况下在赤道上风场、流场和位势场的振幅值与节3.1中的几无差别,且其衰减系数也相同,故此情况下该风场、流场和位势场振幅的经向分布图,各时刻流场的水平分布图,t=0时刻风场、流场和位势场的水平分布图以及赤道上x=0处风场、流场和位势场随时间的变化图,它们均与图1、2、3、4几乎相同,仅需将图2、4说明中T=1a更改为T=4a。这样年际变化的各图就不需再给出了,相应对这些图的解释也不再赘述。
3.3 MJO强迫的Kelvin波
MJO(Madden-Julian Oscillation,季节内振荡)是热带大气最强的振荡信号,其振荡周期为40—60 d,其风场异常大致为2.4~2.8 m/s,MJO活动和异常对热带气候有重要影响;MJO有4个高值区,分别位于赤道西太平洋、赤道东太平洋、南亚热带地区和赤道西大西洋;MJO与全球大气环流与热带积云对流有关,且大多表现为向东传播[16-17]。以下考察MJO强迫下的赤道Kelvin波异常;为此计算中取以下参数:振荡周期T=40 d,赤道上风场异常ua=2.4 m/s,δa=6×10-11/m2,纬向风异常的纬向波长L=3 000 km,约化重力加速度g′=6×10-4m/s2。此时相应有ω=1.818×10-6/s,ka=2.094 4×10-6/m,ca=0.868 1 m/s。除上述参数外,其他参数均同节3.1。在此δa取得较节3.1中大,是因为MJO振荡在太平洋位于赤道上,南北范围不大[17]。采用以上参数计算的结果为:赤道上最大的MJO风场、该Kelvin波流场和位势场15.24×10-3m2/s2,此时由(8)式知 Hˉ=276.0 m,这样由MJO强迫的赤道海洋Kelvin波也已到达海洋次表层。

图5 各场振幅的经向分布(纵坐标0处为赤道)
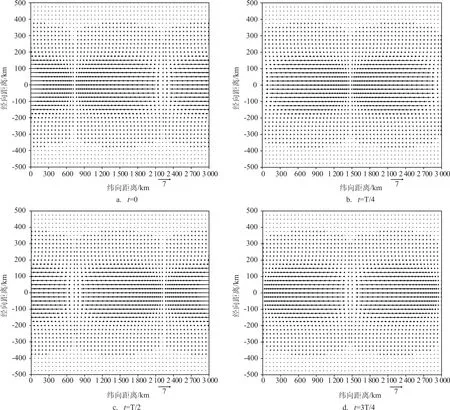
图6 各时刻流场的水平分布(T=40 d,纵坐标0处为赤道,图中箭矢单位:cm/s)
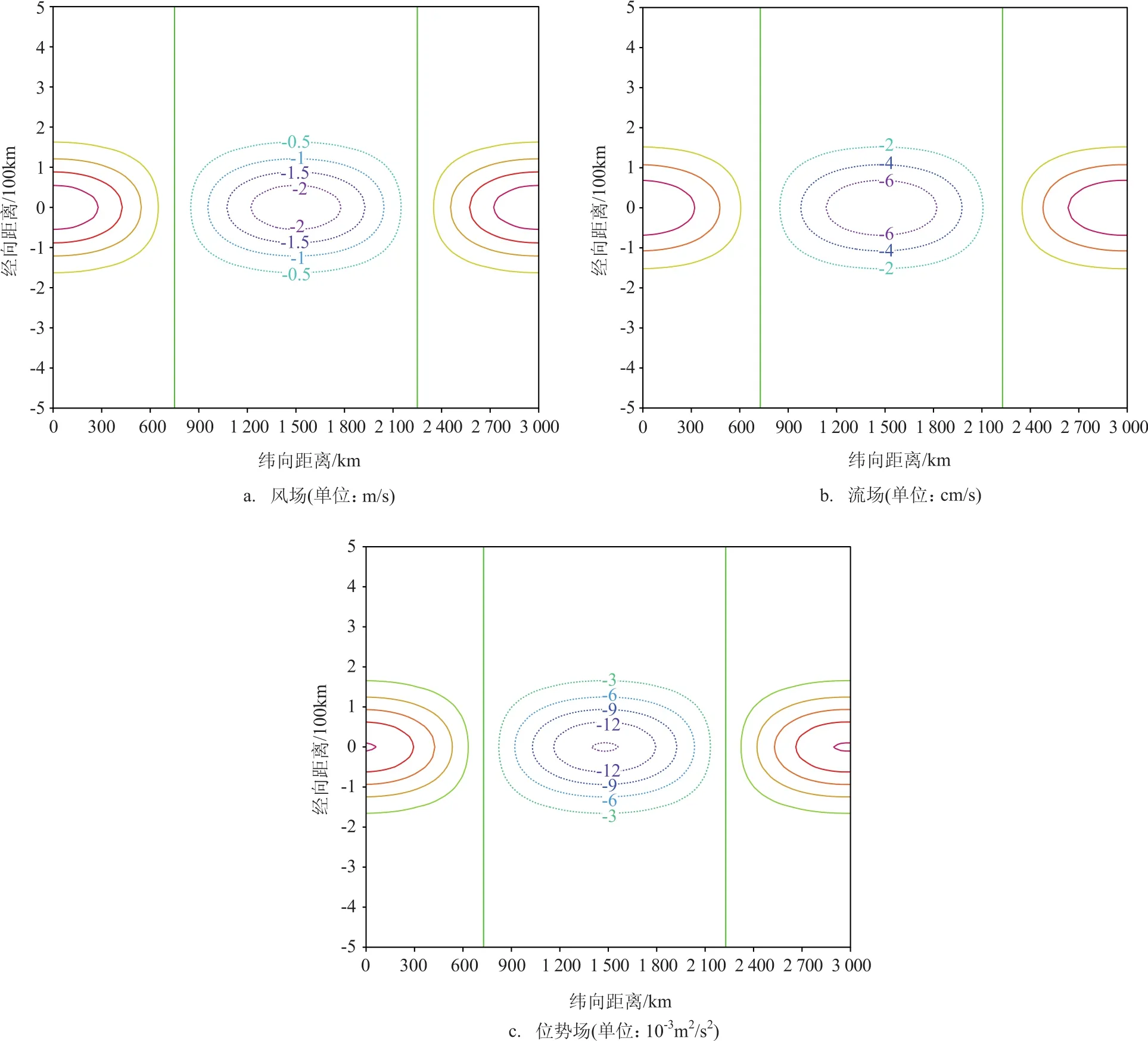
图7 t=0时刻风场、流场和位势场的水平分布(纵坐标0处为赤道)
图5 给出MJO风场,该强迫赤道海洋Kelvin波流场和位势场在各经度上的振幅分布。该风场振幅最大值出现在赤道,为2.4 cm/s,因取的δa较大,其随纬度增加衰减得较图1更快,这也符合MJO位于赤道的事实[17](见图5a)。该强迫赤道海洋Kelvin波流场和位势场的振幅与风场一样,振幅最大值也出现在赤道上,其值分别为7.99 cm/s和15.24×10-3m2/s2,并随与赤道距离的增加而更快衰减(见图5b、c)。
图6给出了以赤道为中心,南北各取500 km计算得到的由MJO强迫的赤道海洋Kelvin波流场。t=0时(见图6a),因MJO风场的波长为3 000 km,故赤道海洋Kelvin波受到该风场强迫,在0~720 km有东向流;在780~2 220 km有西向流;在2 280~3 000 km又为东向流;该东、西向流的极值都出现在赤道上,为7.99 cm/s(见图5b),且该流场随与赤道距离的增加而更快衰减。当t=T 4时(见图6b),则随着该风场的东传,该MJO强迫的赤道海洋Kelvin波流场也相应东传,东向流与西向流的交界已东移至1 500 km处。当t=T 2时(见图6c),该流场随该风场继续东传,此时该流场与t=0时恰好反位相。当t=3T 4时(见图6d),该流场仍在有规律东传,此时该流场与t=T 4时也恰好反位相。当经过1个周期T即40 d后,MJO强迫的赤道海洋Kelvin波流场形态又回到t=0时(见图6a),完成了周期为40 d的循环。
图7给出了t=0时MJO的风场、MJO强迫的赤道海洋Kelvin波流场和位势场的水平分布,图的范围同图6。MJO的风场、该赤道海洋Kelvin波的流场和位势场的最大绝对值都出现在赤道上,且其在赤道南北衰减得更快。与节3.1和节3.2类似,风场与流场两者位相相差不大;在东风强迫区,则有西向流,反之亦然(见图7a、b);而流场与位势场两者则完全同位相(见图7b、c),流场的东向流对应于正位势,反之亦然;前面已指出,这正是正压赤道Kelvin波的特点。在其他时次,与图6相对应,其均有规律东传,40 d后完成一个周期循环。
赤道上x=0处MJO风场、MJO强迫的赤道海洋Kelvin波流场、位势场随时间变化图,其图形分别与图4a、b、c十分类似,仅振幅和周期有所不同[18];在此该风场、该流场和位势场的振幅值分别为 2.4 m/s;7.99 cm/s和15.24×10-3m2/s2,周期T=40 d;故而该图不再给出,相应对该图的解释也不再赘述。
4 讨论
4.1 与经典Kelvin波的比较
现考察强迫赤道海洋Kelvin波与经典Kelvin波的相同之处。两者相同的地方有:
(1)两者的流场均为纬向流,无经向流,均向东传播;
(2)两者的振幅均在赤道上最大,都随着纬度增加呈指数平方衰减。波动为赤道所俘获,表现为赤道波系形态;
(3)两者流场与位势场的配置相同,都呈经典Kelvin波的形式,正位势对应于东向流,反之亦然。
以上这3点也是本文将求得的波动解析解称之为强迫赤道海洋Kelvin波的原因。
现再考察两者的不同之处,其表现为:
(1)经典Kelvin波是自由波动,而强迫赤道海洋Kelvin波则是受风场驱动的强迫波动,其波长、振荡频率以及随纬度的衰减都与该风场相同;
(2)经典Kelvin波是非频散的,其相速与波长无关;而强迫赤道海洋Kelvin波的相速和波长则都与外强迫风场的相同,其是否频散取决于外强迫风场的频散状况;
(3)经典Kelvin波相速确定后,其随纬度增加衰减的程度也随之确定;而强迫赤道海洋Kelvin波的衰减程度却与外强迫风场的衰减程度相同;
(4)外强迫风场的相速及该风场随纬度增加衰减的程度确定后,则强迫赤道海洋Kelvin波的平均水深也随之被确定,即强迫赤道海洋Kelvin波的平均厚度取决于外强迫风场;而经典Kelvin波的平均水深(平均厚度)则是固定的。
4.2 与实况的比较
宣莉莉等[19]指出,5月份赤道东印度洋在2°S~2°N之间出现一支东向急流,流速较大,最大流速可达0.7 m/s,此即春季Wyrtki急流(见文献[19]中图3)。研究还表明,该春季Wyrtki急流是由赤道西风直接驱动的[20]。张东凌等[7]对5月份热带印度洋的大气风场和大洋流场做了联合复EOF分解。此时该分解各模态空间场的大气部分和大洋部分有同一时间系数,它们是同步变化的,这点与强迫赤道海洋Kelvin波相同。在该分解第一模态空间场上,1 000 hPa赤道印度洋为西风控制,而海洋上层流动都被赤道所俘获,在赤道印度洋存在一支窄而强的东向急流,该东向急流与Wyrtki急流非常相像(见文献[7]中图1),也与强迫赤道海洋Kelvin波的形态类似。以上这些都表明Wyrtki急流应与强迫赤道海洋Kelvin波有关。
卢姁等[8]对10月份热带太平洋的大气风场和大洋流场做了联合复EOF分解。在该分解第一模态(ENSO模态)空间场上,1 000 hPa从140°E~130°W的热带太平洋被强西风控制,大洋上层明显流动也都被限制在5°S~5°N之内。在热带太平洋表层2.5°N处,从140°E~130°W则有一支窄而强的东向急流。在其北5°N处此东向急流已明显减弱,在其南的赤道上,此东向急流则已转为偏西向流。此东向急流具有纬向急流的形态(见文献[8]中图1)。此东向急流除其位置稍偏北于赤道外,均与强迫赤道海洋Kelvin波一致,故此东向急流也应与以上强迫赤道海洋Kelvin波有关。
于毅[17]对MJO与El Niño的关系做了研究,指出:热带西太平洋MJO事件的爆发对背景海洋的重要影响就是会强迫出与MJO相关的赤道海洋Kelvin波,其对El Niño事件发生发展有重要影响;每当赤道西太平洋发生强西风异常事件并向中东太平洋传播时,在此后约半年会发生El Nino事件,这是由于其强迫出的赤道海洋Kelvin波东传至赤道东太平洋的缘故;西风异常振幅越大,持续时间越长,之后El Nino事件强度也越强。从3.3节中可知,MJO西风异常越大,该强迫赤道海洋Kelvin波的流场异常和位势场异常也越大,这正与此文献相一致。从3.3节中还可知,MJO强迫出的赤道海洋Kelvin波其相速为0.868 m/s,赤道太平洋东西相距约160个经度,故其东西长度约17 600 km,按该相速计算,此Kelvin波从赤道太平洋西端传到东端需时0.64 a,而这也正与以上的约半年相合,这表明3.3节的结果确实是MJO强迫出的赤道海洋Kelvin波。
由于本文是理想海洋中强迫赤道海洋Kelvin波的解析解,求解时做了一些假定和近似,其与实况有些差异也是很自然的,不过从总体来看,以上强迫赤道海洋Kelvin波与实况及其诊断仍是一致的,实际大洋中该强迫赤道海洋Kelvin波应确实存在。
5 结语
本文采用理想海洋模型,对赤道海洋Kelvin波在纬向风场强迫下的响应即强迫赤道海洋Kelvin波做了解析求解,还与经典Kelvin波和热带大洋的实况和诊断做了对比和讨论,所得主要结果有:
(1)赤道海洋Kelvin波对外强迫风场的响应即强迫赤道海洋Kelvin波的频率、波长和波速都与该风场的相同,在赤道上纬向流的振幅最大,并随纬度增加呈指数平方衰减;外强迫风场越强,强迫赤道海洋Kelvin波也越强,两者呈正比关系;
(2)当外强迫风场的频率和范围确定后,强迫赤道海洋Kelvin波的平均厚度也随之而定,该平均厚度是外强迫风场能够驱动海水的平均水深;外强迫风场的频率越高、纬向波长越长、振幅随纬度增加衰减得越小,则强迫Kelvin波的平均厚度就越大;
(3)在本文所取参数下,该外强迫风场与该强迫赤道海洋Kelvin波流场的位相基本相同。在东风强迫下有西向流,反之亦然;强迫赤道海洋Kelvin波的流场与位势场则完全同位相,东向流对应于正位势,反之亦然,这也是经典Kelvin波的配置;
(4)该强迫赤道海洋Kelvin波与经典Kelvin波两者相同之处有,两者流场均为纬向流,无经向流,均向东传播,振幅均在赤道上最大,表现为赤道俘获波的形态;
(5)该强迫赤道海洋Kelvin波与经典Kelvin波的不同在于,前者是强迫波动,其波长、振荡频率、相速以及振幅随纬度增加衰减的程度均与外强迫风场相同,并被限制在一定的平均水深中,此水深也取决于外强迫风场;而后者是非频散的自由波动,其平均水深是固定的;
(6)将该强迫赤道海洋Kelvin波的解析解与热带大洋的实况以及其诊断做对比后知,两者总体看来一致,实际热带大洋中强迫赤道海洋Kelvin波应确实存在。
[1]Matsuno T.Quasi-geostrophic motions in the Equatorial Area[J].Journal of the Meteorological Society of Japan Series II,1966,44(1):25-43.
[2]Kuo H L.Long-term oscillations in the coupled atmosphere-ocean system and El Niño phenomenon[J].Journal of Climate,1989,2(12):1421-1437.
[3]Lian T,Chen D K,Tang Y M,et al.Effects of westerly wind bursts on El Niño:a new perspective[J].Geophysical Research Letters,2014,41(10):3522-3527.
[4]Hirst A C.Slow instabilities in Tropical Ocean Basin-global atmosphere models[J].Journal of the Atmospheric Sciences,1988,45(5):830-852.
[5]YamagataT,MasumotoY.Asimple ocean-atmosphere coupled model for the origin of a warm El Niño southern Oscillation event[J].Philosophical Transactions of the Royal Society A:Mathematical,Physical and Engineering Sciences,1989,329(1604):225-236.
[6]Zheng F,Zhu J.Observed splitting eastbound propagation of subsurface warm water over the equatorial Pacific in early 2014[J].Science Bulletin,2015,60(4):477-482.
[7]张东凌,曾庆存.5月热带印度洋大气大洋耦合环流的统计动力分析[J].中国科学D辑:地球科学,2007,37(12):1693-1699.
[8]卢姁,张东凌.热带太平洋10月份海气联合复EOF分析[J].海洋通报,2009,28(5):54-63.
[9]Mosquera-Vásquez K,Dewitte B,Illig S.The Central Pacific El Niño intraseasonalKelvin wave[J].JournalofGeophysical Research:Oceans,2014,119(10):6605-6621.
[10]Iskandar I,Mardiansyah W,Setiabudidaya D,et al.Equatorial oceanic waves and the evolution of 2007 positive Indian Ocean Dipole[J].Terrestrial,Atmospheric and Oceanic Sciences,2014,25(6):847-856.
[11]Roundy P E,Kiladis G N.Observed relationships between oceanic Kelvin waves and atmospheric forcing[J]Journal of Climate,2006,19(20):5253-5272.
[12]伍荣生.大气动力学[M].2版.北京:高等教育出版社,2002:256-269.
[13]张永垂,路凯程,张铭.正压准平衡海洋模型及其解Ⅰ:中纬度大尺度风场强迫情况[J].气象科学,2011,31(1):11-16.
[14]张铭.正压涡旋不稳定问题的研究[J].大气科学,1995,19(6):677-686.
[15]张铭,张立凤.球面正压大气的波谱分析[J].水动力学研究与进展,2006,21(1):130-138.
[16]李崇银,潘静,宋洁.MJO研究新进展[J].大气科学,2013,37(2):229-252.
[17]于毅.热带西太平洋大气季节内振荡与El Niño关系研究[D].青岛:中国海洋大学,2010.
[18]Liu T,Chen C C,Milo L.Accurate standard cell characterization and statisticaltiming analysis using multivariate adaptive regression splines[C]∥IEEE.International Symposium on Quality Electronic Design(ISQEP),2015:272-279.
[19]宣莉莉,邱云,许金电,等.热带东印度洋表层环流季节变化特征研究[J].热带海洋学报,2014,33(1):26-35.
[20]Han W Q,McCreary Jr J P,Anderson D L T,et al.Dynamics of the eastern surface jets in the Equatorial Indian Ocean[J].Journal of Physical Oceanography,1999,29(9):2191-2209.
Response of equatorial ocean Kelvin wave to external forcing wind
CHEN Guang-ze1,LU Xu2,3,ZHANG Ming3
(1.Unit 61428,P.L.A,Beijing 100072 China;2.Unit 61741,P.L.A,Beijing 100094 China;3.Laboratory of Atmospheric Circulation and Shortrange Climate Forecast,Meteorological and Oceanological College,P.L.A.University of Science and Technology,Nanjing 211101 China)
Based on the unbounded ideal ocean linear perturbation model,we achieved the analytical solution of anomalous forced Kelvin wave in the equatorial ocean,which was the response of the equatorial ocean Kelvin wave to the anomalies of the forcing zonal wind.The main results were as follows:the frequency,wave-length,and wave celerity of this forced Kelvin wave were the same as the external forcing wind field.The amplitude of zonal flow peaked at the equator and decayed along the meridionality.When the wind field was stronger,the forced Kelvin wave was also stronger.If the frequency and coverage of the wind field were determined,the forced Kelvin wave was limited to a certain average depth.The higher the frequency of the wind field,the longer the zonal wavelength,the smaller the meridional attenuation,then the greater the depth of the water.When the parameter was chosen,the phase of the anomalous wind field and the flow field about the anomalous forced Kelvin wave was almost the same.The forcing of the west wind would cause eastward flow,and vice versa.The phase of the flow field about forced Kelvin wave and the potential field was completely the same.The eastward flow was corresponding to the positive potential,and vice versa,which was the configuration of the classic Kelvin wave.The difference of this Kelvin wave and the classic Kelvin wave was:the former was the dispersive forced fluctuation,which was limited to a certain depth;while the latter was the non-dispersive free fluctuation,whose wavelength,oscillation frequency and the depth of the water were independently set.The analytical solution of the forced Kelvin wave was consistent with the actual and diagnostic analysis of the tropical Indian Ocean and the Pacific Ocean.The forced Kelvin wave should do exist in the actual equatorial ocean.
tropical ocean;Kelvin wave;forcing wind;response;analytical solution
P731.2
A
1003-0239(2017)05-0016-11
10.11737/j.issn.1003-0239.2017.05.002
2016-11-17;
2017-02-28。
国家重点基础研究“973”计划(2013CB956203)。
陈光泽(1983-),男,工程师,硕士,主要从事海气相互作用研究。E-mail:378093084@qq.com
