钢铁企业中具有柔性分组决策的多吊机集成调度问题

谢 谢,郑勇跃,杨文俊

(1.沈阳大学装备制造综合自动化重点实验室,辽宁 沈阳 110044;2.辽宁省标准化研究院,辽宁 沈阳 110004;3.西安交通大学 电子与信息工程学院,陕西 西安 710049)

钢铁企业中具有柔性分组决策的多吊机集成调度问题

谢 谢1,郑勇跃2,杨文俊3

(1.沈阳大学装备制造综合自动化重点实验室,辽宁 沈阳 110044;2.辽宁省标准化研究院,辽宁 沈阳 110004;3.西安交通大学 电子与信息工程学院,陕西 西安 710049)

以钢铁企业炼钢过程为背景,研究了一类具有柔性分组决策的多吊机调度问题.由于该问题是NP难的,在对该问题性质分析的基础上提出了一个启发式算法,对于问题的一个限制情况,证明了启发式的最坏性能,对于一般情况,算法的性能通过计算实验进行了估测.实验结果表明,所提出的启发式算法可以在允许的时间内产生高质量的解.

吊机调度;强NP难;启发式算法

钢铁是迄今为止最广泛使用的金属材料,至今对社会的发展至关重要.自1990年起,中国的钢铁工业取得了实质性的改变和惊人的成就.通常每个公司的钢铁生产计划包括钢包分配、吊机分配以及在生产运输协调调度过程中的吊机调度等.在钢厂的生产实际中,吊机通常和其他运输工具有联系.这些运输工具彼此相互影响.尤其吊机调度大大影响了钢铁生产的完工时间.

每个钢包里已经融化的钢水首先被台车运输,之后再由假设在台车轨道上方的吊机吊至平行放置的转炉中.这个过程对于吊机来说是一个装载移动.当吊机把钢包的钢水倒入后,吊机将空钢包移动到台车后再执行下一次移动.通常钢铁企业生产车间有多个吊机(如图1).吊机沿着区域上方的跨移动同时吊钩沿着跨间的桥移动.这种方法可以使吊钩到达区域上方的任何位置.目标函数为确定吊机的装载移动顺序以最小化所有需求钢水的最大完工时间.

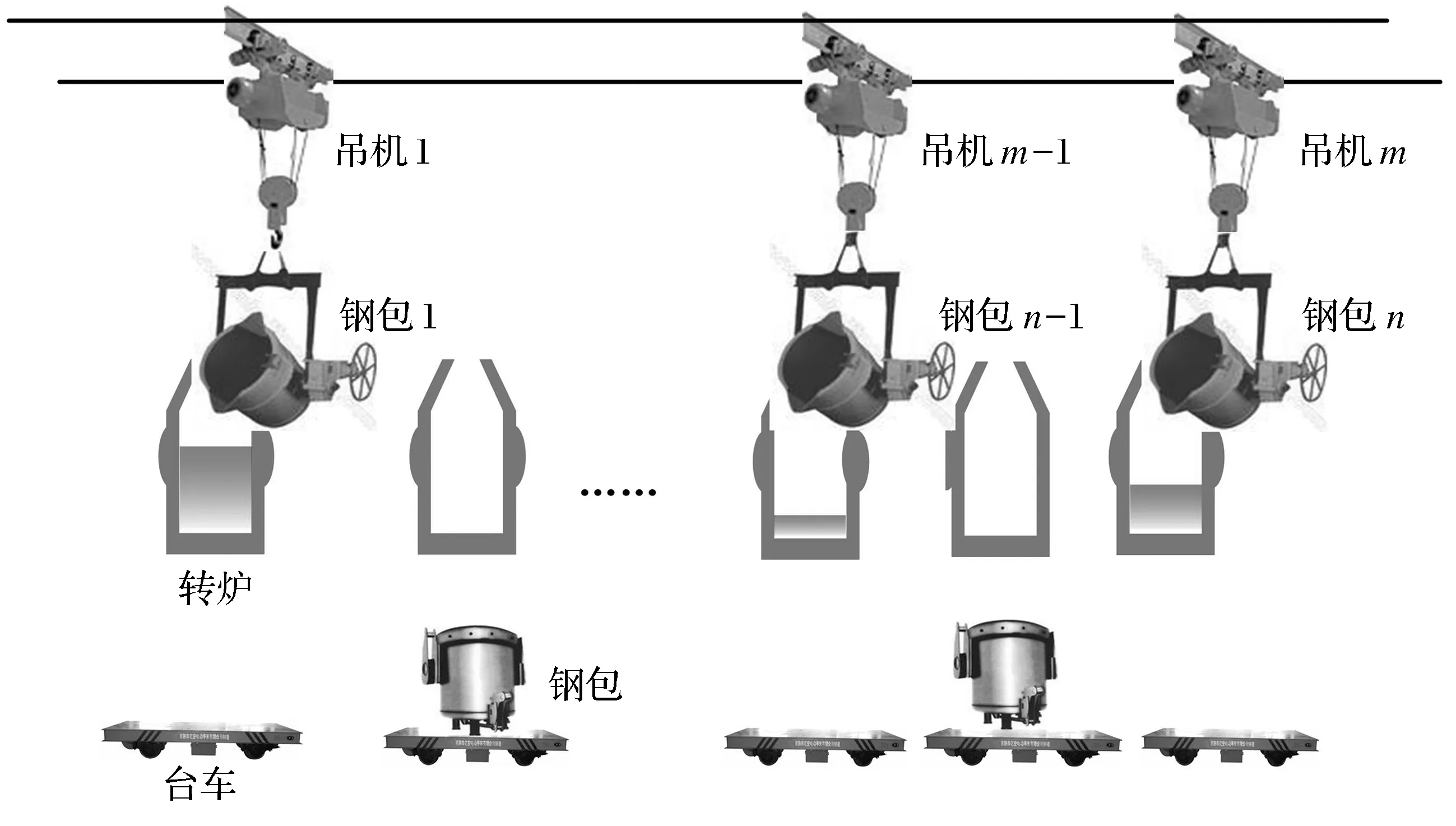
图1 炼钢车间一个区域的多吊机调度问题Fig.1 Multiple crane scheduling problem in the area of the steelmaking shop

大多数关于钢铁企业吊机调度的文献集中在仓库背景中.Zapfel和Wasner[1]首次研究了钢卷仓库中存、取钢卷的单吊机调度问题.他们将吊机调度看做经典车间调度,并建立了一个非线性整规划模型,提出基于局部搜索的启发式算法并通过计算实验测试了算法的性能.已知板卷的到达和需求时间,Rei等人[2]研究了单吊机存取板卷的调度问题以最小化吊机移动的次数.Tang等人[3]考虑了钢卷仓库中板卷倒垛与搬运集成作业的单吊机调度问题,建立混合整数规划模型并分析最优性质,对特殊情况和限制情况分别提出多项式时间最优算法和动态规划算法,对于大规模问题,设计启发式算法并证明该算法的最坏性能.Xie等人[4]设计了一个遗传算法求解该问题,并分析了算法的最坏性能.Xie等人[5]将该问题扩展为多吊机同时调度的情况,建立混合整数规划模型,分析可行性质并给出了下界,设计启发式算法并证明算法的最坏性能.Tang等人[6]对优化板坯及板卷倒垛和存取顺序的吊机调度进行研究,分别建立线性规划模型,提出有效不等式加速模型的求解,对特殊情况提出多项式时间内可解的最优算法、对一般情况提出贪婪的启发式算法并进行最坏性能分析.

对于吊机参与生产的过程,Tanizaki等人[7]研究了炼钢过程的多吊机调度问题,建立混合整数规划模型并提出混合了深度优先和广度优先的启发式算法.Dohn和Clausen[8]研究了板坯计划和吊机调度问题,建模为计划和调度两部分,分别产生吊机从当前状态到目标状态的一系列操作并设计吊机操作开始时间的精确算法.Xie等人[9]以钢卷包装过程为背景,研究了基于重入车间建模策略的吊机调度问题,证明该问题是强NP-难的,分别针对吊机与一台及多台机器衔接的情况,给出启发式算法并证明算法的最坏性能比.Sun等人[10]对炼钢连铸过程的吊机调度问题建立带有混合时间的Petri网模型,并转化为线性模型,使用标准的CPLEX软件求解小规模问题.增加有效不等式改进模型加速搜索获得大规模问题的近优解.针对罩式退火工艺,Moon,Hrymak[11]和Liu等人[12]更注重板卷轧制的过程,几乎没有考虑吊机的调度.Tang等人[13]研究了该过程的单吊机调度问题,建立混合整数规划模型,证明问题是强NP-难的,分析最优性质并设计启发式算法,对算法的绝对性能进行了理论分析,针对特殊情况,分别给出多项式时间内可解的最优算法.谢等人[14]与谢和郑[15]分别针对参与钢铁企业中不同生产活动的多吊机调度问题进行了研究,不同于本文的研究,他们并没有将吊机调度分组决策并调度.

迄今为止,以上文献只是将吊机调度分开考虑,并没有对其进行分组决策.本文研究了具有柔性分组决策的多吊机集成调度问题以最小化给定的需求钢包的最大完工时间.由于吊机都在同一跨上运行,因此需要满足不交叉约束.

1 问题定义和描述

研究了具有不交叉约束的多吊机调度问题以最小化需求钢包的最大完工时间.假设钢包从左至右依次编号1,2,…,n(见图1).一台吊机一次只能服务一个钢包.本文中,提起一个需求钢包并移动到指定转炉称为一次吊机操作.在这个操作中一个钢包需要从台车处被提起,移动到转炉位置然后将钢包内钢水倾倒其中.整个过程对于吊机来说称为一次装载移动.钢包内钢水倾倒后吊机将空包移动回台车处,之后吊机空移动到另一台车去进行下一个装载移动.对于给定的需求的钢包集合,探究了多吊机集成调度问题以确定每一台吊机装载移动的顺序.目标函数为最小化最大完工时间,也就是说,最小化所有钢包倾倒结束时的完工时间.

令A为区域内所有位置的集合,每个位置q∈A可以由它的行-列-高度坐标独一无二地表示为(rq,cq,hq).文中的其余部分,用号码或者坐标便于表示位置.由于位置可以由坐标独一无二地表示,因此每个移动可以表示为以下两种方式:toq≡trocoho,rqcqhq,eoq≡erocoho,rqcqhq.

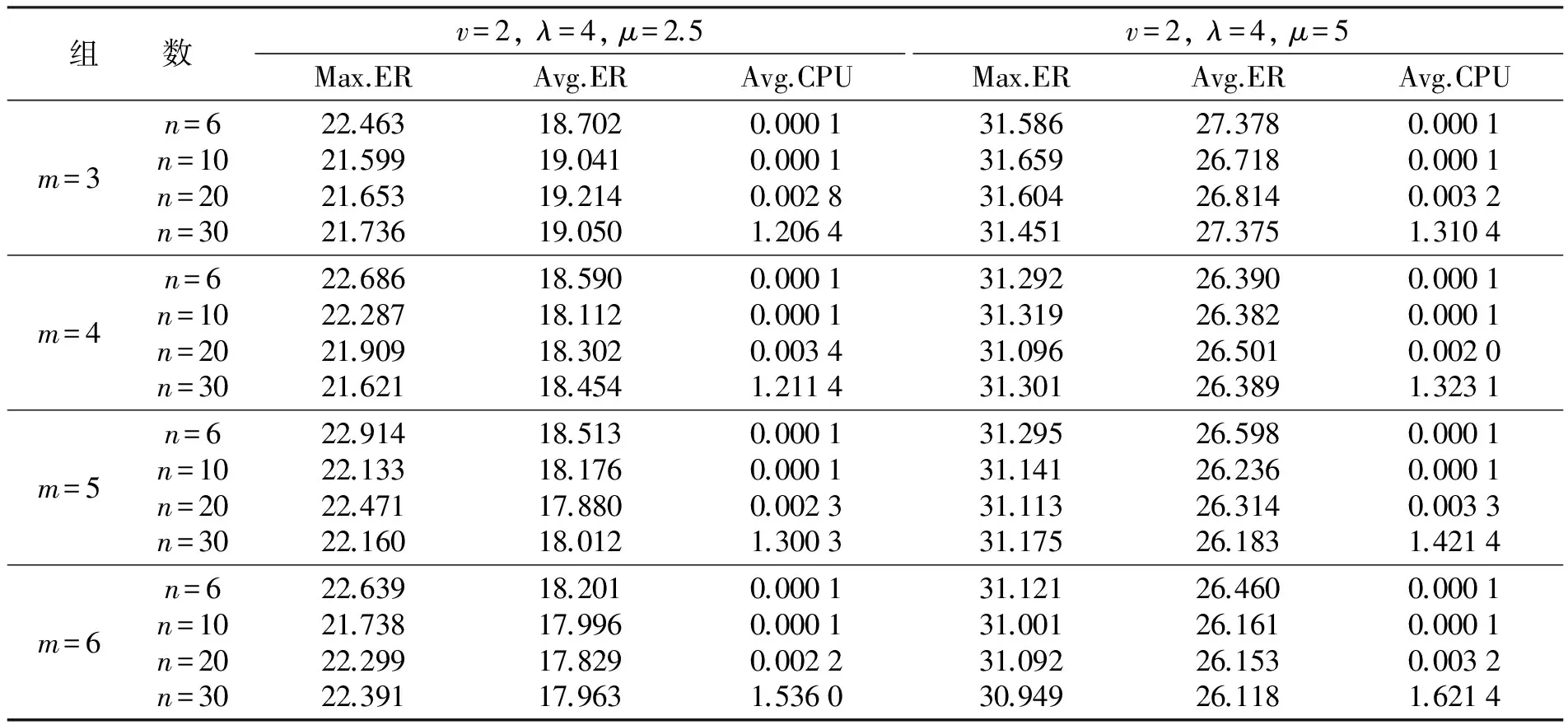
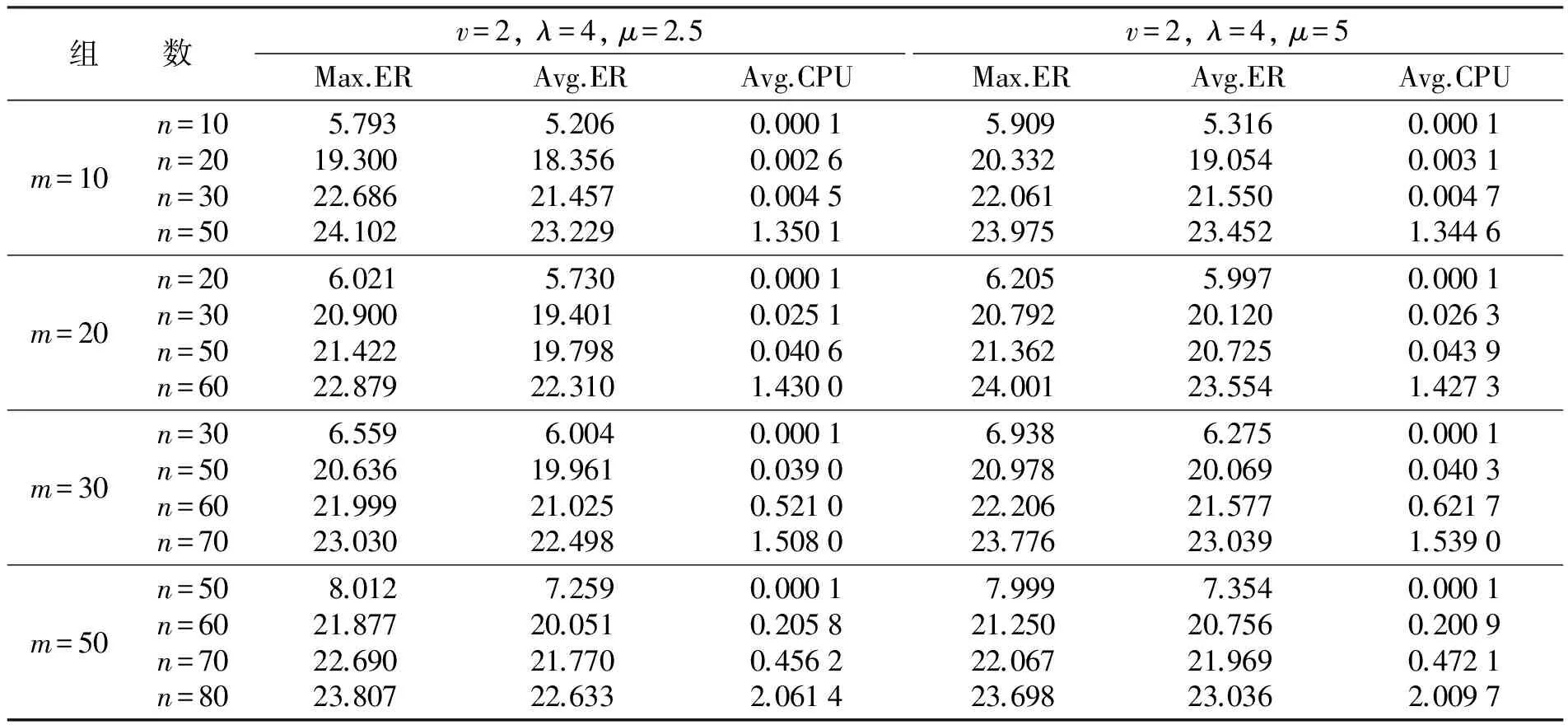
令第j个钢包的操作时间为pj>0,为方便表达,假设吊机从左至右编号为1,2,…,m(见图1).注意操作时间包括吊机上提下放的装载移动或空移动.问题就是确定一个顺序以决策每一个钢包j的开始时间sj.由于吊机的不交叉约束,策略可行是指当且仅当任意两钢包j,j′,满足j

为了便于参阅,将上下文提到的全部符号列表总结如下,一些需要进一步使用的符号将在需要的时候给予定义.

n——钢包数量,钢包从左至右依次编号为1,2,…,n;

A——区域内所有位置的集合;

q∈A——每个位置q的行-列-高度坐标(rq,cq,hq);

toq——位置o和q之间的装载移动时间,由于每个位置可以用坐标独一无二地表示,因此toq≡trocoho,rqcqhq;

eoq——位置o和q之间的空移动时间,由于每个位置可以用坐标独一无二地表示,因此eoq≡erocoho,rqcqhq;

m——吊机数量,从左至右依次编号为1,2,…,m;

sj——吊机移动钢包j的开始时间;

σ(j)——操作钢包j所分配的吊机号;

CA和C*——分别为由算法A产生的函数值和最优目标值.

基于对问题的分析,可得到如下性质:

性质1 任意时刻第i个吊机操作第j个钢包,既不存在吊机i′,其中i′>i,可以操作钢包j′满足j′≤j,也不存在吊机i″,其中i″

为了简化,令

进一步令CA和C*分别为由算法A产生的函数值和最优目标值.类似于平行机调度问题,可以得到如下性质:

性质2 最优目标值的下界LB为

即使不考虑问题的柔性分组决策,当吊机的数目m≥2时,Lim等[16]证明本文研究的问题已经是NP-难的,几乎不可能在可接受的时间内求得实际问题的例子,因此使用启发式算法是合适的,不必找到最优解,至少可以在可接受的时间内找到可行解.提出如下的启发式算法.

2 启发式算法

提出一个有效的启发式算法.该算法将钢包从左至右划分为m个子集,每个子集与其中一个吊机相独立,保证每个集合不太大.算法开始于每个吊机无排序,或已经分配了一个钢包的吊机当时正操作一个钢包,每次分配钢包给吊机,一个新的划分解则产生了.

为了表示如下提出的启发式算法,令组Ω1,Ω2,…,Ωm为调度过程m个不相交的子集.σ=(1,2,…,n)为n个钢包的顺序,将n个钢包划分为m个互不相交的子集.(rm0,cm0,hm0)为动态参数,用来表示吊机m的初始位置以及在任何阶段中吊机的当前位置.启发式过程如下:

第1步 如果Ω1=∅,计算满足如下条件的钢包号:

即从最左侧钢包开始,依次作为第一组,该组内的钢包由最左侧吊机操作.

第2步 类似地,如果Ω2=∅,计算满足如下条件的钢包号:

从第k+1个钢包起,依次作为第二组,该组内的钢包分配给左侧第二个吊机.

第3步 在每一组内,选择满足(erm0cm0hm0,rjcjhj+trqcqhq,rjcjhj)为最小的钢包j,其中trqcqhq,rjcjhj为移动钢包j到最近的空位q的时间.一旦时间相同,优先分配给最左侧的吊机.任何相同情况的产生,则选择erm0cm0hm0,rjcjhj为最小的钢包.意味着0时刻起从第一个钢包到最后一个,一旦吊机空闲,则通过尽快将每个钢包分配给吊机创建一个排序.

第4步 如果Ω1∪Ω2∪…∪Ωm=∅,则停止,否则,转第3步.

第1步、第2步钢包的划分需要耗时最多.第3步吊机的调度过程最多需要O(mnA).因此启发式的计算复杂性为O(mn2A).在下一部分中,将进一步分析算法的计算性能.

由于算法将钢包的子集分配给每个可获得的吊机,最大完工时间则由其中一个子集决定.更精确地说,可由最大总加工时间决定.如果没有划分太多的子集,并且每个子集内的总加工时间不太大,则如下的观察进一步证明了所提出算法的界在2-2/m+1之内.

性质3 如果启发式最多划分m组,则每组的全部调度时间不超过CH≤max{2P/m+1,pmax},结合C*≥max{P/m,pmax},则CH≤2(1-1/m+1)C*.

3 计算结果

对所提出的启发式算法进行实验以检验其有效性.算法采用C# 5.0语言编程,并且根据钢铁企业生产实际的数据求解了一系列问题的实例.这个算法在内存为8 192 MB RAM和i7-3770 3.4 GHz的x64位计算机上用Visual C++语言编码进行了测试.

对于每个实例,满载移动的时间在[30,180]之间离散平均分布随机生成;空载移动的时间在[10,60]之间离散平均分布随机生成;钢包和吊机的数目分别在[6,30]和[3,6]之间随机产生,吊机的装载移动和空载移动时间分别为v=2和λ=4.吊机上提或下放钢包的时间为μ=2.5.对每一组例子,偏差率定义为(Cmax-LB)/LB×100%.平均偏差(Avg.ER)和最大偏差(Max.ER)用于评估算法的平均性能.结果见表1,其中最优值由性质2的下界进行了估测.为了测试吊机上提下放时间与距离无关,将该值增加一倍又测试了各实例.为了进一步测试算法的计算性能,将问题中钢包和吊机的数目扩大,估测算法在大规模试验中的性能,随机生成了500个实例,结果见表2.

表1 启发式算法与下界比的平均偏差最大偏差Table 1 Average optimality gaps of the lower bounds with respect to the heuristic algorithm

表2 启发式算法求解大规模问题所得下界比的平均偏差最大偏差Table 2 Average optimality gaps of the lower bounds with respect to the heuristic algorithm for solving big instances

计算结果表明算法求解中小规模实例最多在1.621 4s的CPU时间内求得问题的近优解,即使求解大规模问题,平均偏差也不超过25%.因此,所提出的算法可以快速求解任意测试的实例(见表1),随着钢包数目的增加偏差逐渐减小.其中一个原因或许是钢包的数目越多,等待时间越短.当吊机的上提下放时间变大时,偏差也增大了.当增加时,意味着增加了目标函数的常数部分使得目标值与下界的比值变小了(见表2).当钢包与吊机数目相同时,算法可以在很短时间内求解大规模问题的实例,一个可能的原因是算法省略了吊机分组,随着钢包数目的增加,吊机的柔性分组过程增加了目标值,从而使算法的偏差逐渐增大.结合表1和表2,当吊机的上提下放时间很少时而仅存在移动钢包的时间,问题的求解就更有效.

4 结 论

研究了钢铁企业炼钢过程的具有柔性分组决策的多吊机调度问题.在该过程中吊机将每个装满钢水的钢包吊至并倒入转炉开始加工,目标函数为确定吊机的装载移动顺序以最小化所有需求钢水的最大完工时间.提出一个启发式算法.对于问题的一个限制情况,证明了启发式算法最坏性能比,对于一般情况,根据生产实际数据,实施计算实验.计算结果表明,所提出的启发式算法可以快速求得问题可接受的解.

[1]ZPFELG,WASNERM.Warehousesequencinginthesteelsupplychainasageneralizedjobshopmodel[J].InternationalJournalofProductionEconomics,2006,104(2):482-501.

[2]RUIJR,KUBOM,PEDROSOJP.Simulation-basedoptimizationforsteelstacking[C]∥Modelling,ComputationandOptimizationinInformationSystemsandManagementSciences,SecondInternationalConference,MCO2008,Metz,France-Luxembourg,September8-10,2008.Proceedings.DBLP,2008:254-263.

[3]TANGLX,XIEX,LIUJY.Craneschedulinginawarehousestoringsteelcoils[J].IieTransactions,2014,46(3):267-282.

[4]XIEX,ZHENGY,LIY.Geneticalgorithmanditsperformanceanalysisforschedulingasinglecrane[J].DiscreteDynamicsinNatureandSociety,2015:1-12.

[5]XIEX,ZHENGY,LIY.Multi-craneschedulinginsteelcoilwarehouse[J].ExpertSystemswithApplications,2014,41(6):2874-2885.

[6]TANGL,ZHAOR,LIUJ.Modelsandalgorithmsforshufflingproblemsinsteelplants[J].NavalResearchLogistics,2012,59(7):502-524.

[7]TANIZAKIT,TAMURAT,SAKAIH,etal.Aheuristicschedulingalgorithmforsteel-makingprocesswithcranehandling[J].JournaloftheOperationsResearchSocietyofJapan,2006,3(3):188-201.

[8]DOHNA,CLAUSENJ.Optimisingtheslabyardplanningandcraneschedulingproblemusingatwo-stageheuristic[J].InternationalJournalofProductionResearch,2010,48(15):4585-4608.

[9]XIEX,TANGL,LIY.Schedulingofahubreentrantjobshoptominimizemakespan[J].InternationalJournalofAdvancedManufacturingTechnology,2011,56(5/6/7/8):743-753.

[10]SUNLL,LIUW,CHAITY,etal.Craneschedulingofsteel-makingandcontinuouscastingprocessusingthemixed-timedpetrinetmodellingviaCPLEXoptimization[C]∥Proceedingsofthe18thIFACWorldCongress,Milano,Italy,2011:9482-9487.

[11]MOONS,HRYMAKAN.Schedulingofthebatchannealingprocess-deterministiccase[J].Computers&ChemicalEngineering,1999,23(9):1193-1208.

[12]LIUQL,WANGW,ZHANHR,etal.Optimalschedulingmethodforabell-typebatchannealingshopanditsapplication[J].ControlEngineeringPractice,2005,13(10):1315-1325.

[13]TANGL,XIEX,LIUJ.Schedulingofasinglecraneinbatchannealingprocess[J].Computers&OperationsResearch,2009,36(10):2853-2865.

[14] 谢谢,郑勇跃,李彦平.工件和工具混合搬运的多吊机调度问题[J].沈阳大学学报(自然科学版),2016,28(4):291-295.

XIEX,ZHENGYY,LIYP.Jobandtoolmixedtransportationbasedmulti-craneschedulingproblem[J].JournalofShenyangUniversity(NaturalScience),2016,28(4):291-295.

[15] 谢谢,郑勇跃.带有机器卸载不延误约束的多吊机调度问题[J].沈阳大学学报(自然科学版),2017,29(2):118-124.

XIEX,ZHENGYY.Multiplecraneschedulingwithno-delayconstraintsformachineunloading[J].JournalofShenyangUniversity(NaturalScience),2017,29(2):118-124.

[16]LIMA,RODRIGUESB,XUZ.Am-parallelcraneschedulingproblemwithanon-crossingconstraint[J].NavalResearchLogistics,2007,54(2):115-127.

Multiple-CraneIntegratedSchedulingProblemwithFlexibleGroupDecisioninaSteelmakingShop

XieXie1,ZhengYongyue2,YangWenjun3

(1.Key Laboratory of Manufacturing Industrial and Integrated Automation,Shenyang University,Shenyang 110044,China;2.Liaoning Institute of standardization,Shenyang 110004,China;3.School of Electronic and Information Engineering,Xi’an Jiaotong University,Xi’an 710049,China)

Based on the steelmaking process of iron and steel enterprises,a class of multiple-crane scheduling problem with flexible packet decision-making was studied.For this demonstrated NP-hard problem,a heuristic algorithm based on some analyzed properties was proposed.For a restrict case,the worst-case performance was analyzed.For the general case,the average performance of the heuristic algorithm was computationally evaluated.The results show that the proposed heuristic algorithm is capable of generating good quality solutions.

crane scheduling;NP-hard;heuristic algorithm

2016-05-23

国家自然科学基金资助项目(71672117);辽宁省自然科学基金资助项目(201602526);辽宁省高等学校杰出青年学者成长计划资助项目(LJQ2014133).

谢 谢(1981-),女,辽宁沈阳人,沈阳大学副教授,博士.

2095-5456(2017)05-0389-05

TG 338

A

【责任编辑:李艳】