平衡超立方体的故障容错性

2017-11-10张欣欣许力林丽美

网络与信息安全学报 2017年9期

张欣欣，许力，林丽美,3

平衡超立方体的故障容错性

张欣欣1,2，许力1,2，林丽美1,2,3

（1. 福建师范大学数学与计算机科学学院，福建福州 350007；2. 福建省网络安全与密码技术重点实验室，福建福州 350007；3. 福建农林大学计算机信息学院，福建福州 350002）

故障容错是衡量多处理器互连网络可靠性的重要方式之一。其中-限制边连通度和-限制连通度保证了剩下每个分支之间不连通且每个分支中节点的邻居数目不少于，能够更加精准地测量多处理器和多信道系统的容错性和可靠性。平衡超立方体是超立方体的一个变形，它特有的良好拓扑性质能够更好地满足多处理器系统和多种新型网络的需要。提出了维平衡超立方体的{1,2}-限制边连通度和{1,2}-限制连通度，能够丰富以平衡超立方体为拓扑结构的网络容错性和可靠性的评价体系，并为平衡超立方体的故障诊断算法打下良好基础。

故障容错性；限制连通度；限制边连通度；平衡超立方体

1 引言

连通度（边连通度）测量容错性有3个明显的缺陷：① 2个网络的连通度（或边连通度）即使相同，它们的可靠性也不一定一样，因为它们的最小点割（或最小边割）故障概率可能不同；②连通度（边连通度）不能准确地反映由于处理机（或通信信道）损坏造成的系统损坏程度；③在分析和应用这2个参数时，本文不言而喻地假定了系统的任何部件都可能同时失灵[4]。为了弥补以上缺陷，人们对传统的连通度（边连通度）概念加以推广，以适应网络容错性分析的需要。本文研究的限制边连通度和限制连通度就是连通度和边连通度的推广。

超立方体被称为并行计算系统中最流行的互连网络拓扑结构之一,Bhuyan[18]提出了各种性能优良的超立方体网络的变形，经过多年的发展，新型互连网络已经提出一系列的拓扑结构，包括折叠立方网络、交叉立方网络、交换立方网络、分层立方网络和平衡超立方网络等。由Wu和Huang[19]提出的平衡超立方体增强了超立方体的一些性质。平衡超立方体中每个点都有一个与自己邻点相同的匹配节点，故在平衡超立方网络中一个故障节点的运行任务可以转化给它的匹配节点完成[20]。迄今为止，平衡超立方体的容错性与可靠性研究尚未求出。

2 平衡超立方体的定义与性质

平衡超立方体的定义由Wu和Huang[19]用2种方式提出。

图1是一维平衡超立方体和二维平衡超立方体的结构图。

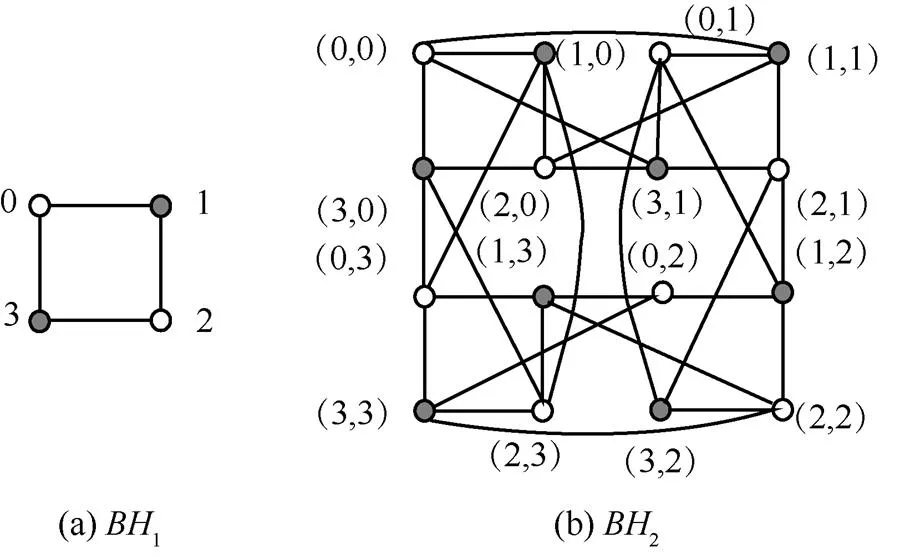
图1 一维和二维平衡超立方体结构

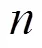
3 平衡超立方体的限制边连通度

图2 ，都不在S中

4 平衡超立方体的限制连通度

图3 圈C的邻边集

图4 圈C的邻点集

图5 F是的2-限制点割

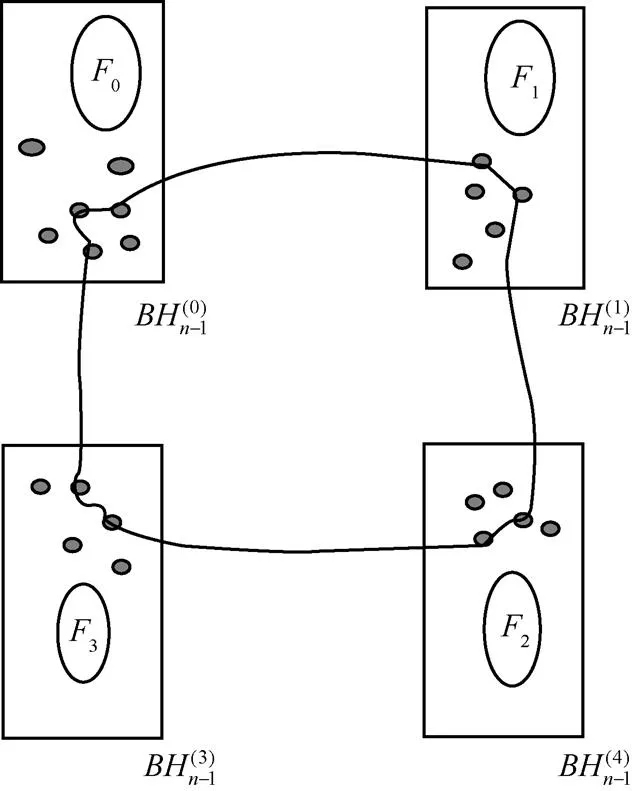
图6 是连通的

图7 是连通的

图8 是连通的

图9 是连通的

图10

图11

5 结束语

[1] 包国华, 王生玉, 李运发. 云计算中基于隐私感知的数据安全保护方法研究[J]. 信息网络安全, 2017(1):84-89. BAO G H,WANG S Y, LI Y F. Research on privacy aware data security protecting method in cloud computing[J]. Netinfo Security, 2017(1):84-89.

[2] 周涛, 柏文洁, 汪秉宏, 等. 复杂网络研究概述[J]. 物理, 2005, 34(1): 31-36. ZHOU T, BAI W J,WANG B H, et al. Overview of complex network Research[J]. PHYSICS, 2005, 34(1): 31-36.

[3] 滑楠, 曹志刚. 无线认知网络概念与实例研究[J]. 计算机工程与应用, 2009, 45(2): 1-6. HUA N, CAO Z G. The concept and examples of wireless cognitive Network[J]. Computer Engineering and Applications, 2009, 45(2): 1-6.

[4] 徐俊明. 组合网络理论[M]. 北京: 科学出版社, 2007.

XU J M, Combinatorial theory in networks[M]. Beijing: Science Press,2007.

[5] 徐俊明. 图论及其应用[M]. 合肥: 中国科学技术出版社, 2010.

XU J M, Graph Theory with Applications[M]. Hefei: Science and Technology of China Press,2010.

[6] XU J M, ZHU Q, XOU X M, et al. On restricted connecti-vity and extra connectivity of hypercubes and folded hypercubes[J]. Journal of Shanghai Jiaotong University (Science), 2005, 10(2): 203-207.

[7] LIN L M, XU L, ZHOU S M, et al. The extra, restricted connectivity and conditional diagnosability of split-star networks[J]. IEEE Transactions on Parallel and Distributed Systems, 2016, 27(2): 533-545.

[8] LIN L M, ZHOU S M. Conditional connectivity for (n, k)- arrangement graphs[J]. Journal of Mathematical Study, 2012, 45(4): 350-364.

[9] 林丽美, 周书明, 许力. 分层立方网络的/-诊断度和诊断算法[J]. 山东大学学报(理学版). 2013, 48(7):85-92. LIN L M, ZHOU S M, XU L./- diagnosability and diagnosis algorithm for hierarchical cube networks[J]. Journal of Shandong University(Natural Science), 2013,48(7):85-92.

[10] ZHOU S, CHEN L, XU J M. Conditional fault diagnosability of dual-cubes[J]. International Journal of Foundations of Computer Science, 2012, 23(8): 1729-1748.

[11] ZHOU S, XU J M. Conditional fault tolerance of arrangement graphs[J]. Inform Process. 2011, 111(21): 1037-1043.

[12] ZHU Q, XU J M. On restricted edge connectivity and extra edge connectivity of hypercubes and folded hyper cubes[J]. Journal of University of Science and Technology of China, 2006, 36(3): 249-251.

[13] PAN X F, XU J M, LV M. On restricted connectivity of some cartesian product graphs[J]. Journal of University of Science and Technology of China, 2006, 36(3):237-240.

[14] 王国亮, 师海忠. 完全对换网络的限制连通度[J]. 运筹学报, 2013, 17(3): 57-64.

WANG G L, SHI H Z. The restricted connectivity of completely switched networks[J]. Operations Research Transactions, 2013, 17(3): 57-64.

[15] 马强, 梁家荣, 熊茜, 等. 交换交叉网络的可靠性研究[J]. 高技术通讯, 2015, 25(10):919-926.

MA Q, LIANG J R, XIONG Q, et al.Research on reliability of switched cross networks[J]. High Technology Letters,2015, 25(10): 919-926.

[16] XU J M, LV M, FAN Y M. The restricted edge-connectivity of de Bruijn undirected graphs[J]. Ars Combinatoria Waterloo then Winnipeg, 2008, 83(1):321-333.

[17] 徐俊明，点可迁图的限制边连通度[J]. 数学年刊A辑(中文版), 2000, 21(5):266-272.

XU J M. Restricted edge connectivity of vertex transitive graphs[J]. Chinese Annals of Mathematics,Series A.2000, 21(5):266-272.

[18] BHUYAN L N, AGRAWAL D P. Generalized hypercube and hypercube structures for a computer network[J]. IEEE Trans Computers, 1984,32(4):323-333.

[19] WU J, HUANG K. The balanced hypercube: a cube-based systemhemat for fault-tolerant applications[J]. IEEE Transactions Comput, 1997, 46(4): 484-490.

[20] ZHOU J X, WU Z L, YANG S C, et al. Symmetric proper and reliability of balanced hypercube[J]. IEEE Transactions Comput, 2015, 64(3): 876-881.

[21] LU H Z. On extra connectivity and extraedge-connectivity of balanced hyper cubes[J]. International Journal of Computer Mathematics, 2016, 94(4): 813-820.

[22] YANG M C. Super connectivity of balanced hyper cubes[J]. Applied Mathematics and Computation, 2012, 219(3): 970-975

Fault tolerance of balanced hypercubes

ZHANG Xin-xin1,2, XU Li1,2, LIN Li-mei1,2,3

(1. School of Mathematics and Computer Science, Fujian Normal University, Fuzhou 350007, China;2. Fujian Provincial Key Laboratory of Network Security and Cryptology, Fuzhou 350007, China;3. College of Computer and Information Science, Fujian Agriculture and Forestry University, Fuzhou 350002, China)

Fault tolerance is one of the important ways to measure the reliability of multiprocessor interconnection networks.-restricted edge connectivity and-restricted connectivity can ensure every remaining component is disconnected , the number of neighbors of vertex is no less than, which can measure the fault tolerance and reliability of multiprocessor and multichannel system more accurately. Balanced hypercubes is a variant of the hypercube, which has some specific topological properties, it can better meet the needs of the multiprocessor system and many new networks. The {1,2}-restricted edge connectivity and the {1,2}-restricted connectivity of balanced hypercubes were proposed, which could enrich the evaluation system of network fault tolerance and reliability in balanced hypercubes topology and it laid a good foundation for the fault diagnosis algorithm of balances hypercube.

fault tolerance, restricted connectivity, restricted edge-connectivity, balanced hypercubes

O157.5

10.11959/j.issn.2096-109x.2017.00193

2017-06-15；

2017-08-17。

许力，Xuli@fjnu.edu.cn

国家自然科学基金资助项目（No.61771140, No.U1405255, No.61702100）；福州市科技局基金资助项目（No.2015-G-59）；福建省高校产学合作科技重大基金资助项目（No.2017H6005）；福建省教育厅基金资助项目（No.JAT160123）；中国博士后面上基金资助项目（No.2017M612107）

The National Natural Science Foundation of China (No.61771140, No.U1405255, No.61702100), Fuzhou Science and Technology Bureau Project (No.2015-G-59), University Industry Cooperation of Major Science and Technology Project of Fujian Province (No.2017H6005), Fujian Provincial Education Department Project (No.JAT160123), Post-doctoral Science Foundation of China (No.2017M612107)

张欣欣（1993-），女，河南罗山人，福建师范大学硕士生，主要研究方向为网络与信息安全。