三塔斜拉桥的动力特性研究
2017-11-09杨海涛
杨海涛
(山西省长治公路管理段,山西 长治 046000)
斜拉桥具有很强的跨越能力,且具有结构受力合理,施工技术成熟的优点。在方案对比阶段相对连续刚构及悬索桥而言具有很强的竞争力。随着我国桥梁建设中对结构的美观要求越来越高,斜拉桥索塔形式也越来越多样化[1]。在建设工程中常见的斜拉桥索塔形式有A形、门式、柱式、倒Y形及菱形等,本桥采用的海豚形索塔在国内的斜拉桥中尚属首次。而索塔的结构形式对斜拉桥动力特性有直接的影响。因此,对该种索塔的斜拉桥动力特性进行分析是十分必要的。
1 工程概况
本桥采用三塔六跨钢箱梁平行单索面的结构形式,其跨径布设为:110+129+258+258+129+110=994 m;主梁采用大悬臂倒梯形整体式钢箱梁,梁高4.5 m;3个索塔外轮廓造型一致,均为海豚型造型。大桥的桥型布置图见图1,索塔一般构造图见图2。主副塔均为圆曲线的双曲海豚塔,主塔最低端的部分采用的是钢混结构,索塔的其他部分采用钢结构,该索塔为钢混组合结构。主塔为直线,副塔为圆曲线;海豚塔采用钢结构。
该桥结构体系为三塔六跨的半漂浮体系,在竖向主梁与主塔、桥墩之间均设置拉压球形钢支座;在纵向主梁与主塔、桥墩之间设置阻尼装置;在横向1号墩、3号索塔、5号索塔、7号墩处布设横向抗风支座;4号索塔处布设阻尼装置;2号墩、6号墩设置滑动支座。

图1 桥型布置图
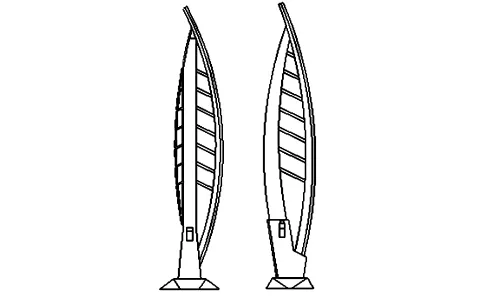
图2 索塔构造图
2 斜拉桥的有限元模型
众所周知,桥梁结构的动力响应受外界环境因素的作用以及结构本身所固有的动力特性的影响。因此分析结构在外部作用下(如地震、风等因素)的结构响应,首先应先对结构的动力特性进行计算分析[2-3]。
结构动力特性主要由结构的固有频率和结构的振型,以及结构的阻尼3部分组成,它们均是结构自身所具有的属性。主梁的截面特性、主塔和主梁刚度的比值、主塔与主梁的连接方式、斜拉索的空间布设形式、辅助墩数量及其位置等多种因素对斜拉桥的动力性能的影响都很大[4-5]。
2.1 空间有限元模型的建立[6]
结构ANSYS模型如图3所示。主梁和桥塔采用Beam4单元进行模拟,根据实际截面特性和刚度将主梁简化为单主梁模型,对于质量系统的模拟是将其主梁的质量分配到主梁单元的两端节点上,其中集中质量矩用来考虑主梁的扭转惯矩,其他的附属构造等通过集中质量元来模拟其对主梁平动质量和转动惯量;用Link10单元对斜拉索进行模拟,并采用Ernst公式对斜拉索的垂度效应进行修正[7],以确保拉索模拟的精确性;用软件中的耦合功能,采用主从节点连接的方式来模拟结构中的固定支座、横向抗风支座、滑动支座等边界条件,其他的自由度关系用节点耦合进行模拟。

图3 结构计算分析有限元模型
2.2 动力特性分析基本方程[8]
斜拉桥的结构体系具有质量和刚度连续分布的特点,且为多自由度体系,根据上述的有限元计算模型,对该桥的不同结构部分进行相应的简化处理后,将结构离散成具有有限自由度的有限元计算模型。阻尼对结构自振特性影响不大,在计算结构振型和固有频率时可不考虑阻尼的影响[4]。假设结构的自由度为n,则该体系的自由振动可用式(1)来表示[9]:

式(1)的特征方程可表示为:

由于位移是任意的,应满足:

由式(3)可求得结构的n阶自振频率,然后将自振频率代入式(2)即可得到相应的振型或固有模态。
结构动力分析求解方法众多,本文采用改进的经典Lanczos方法(Block Lanczos)方法求解系统的特征值问题[10]。
2.3 桥塔对结构动力特性的影响
在分析上述两种桥塔模型的基础上,分别计算得到双曲海豚塔和单直单曲海豚塔下斜拉桥的自振特性结果,两种塔形前15阶的结构自振频率与模态分别如表1所示。
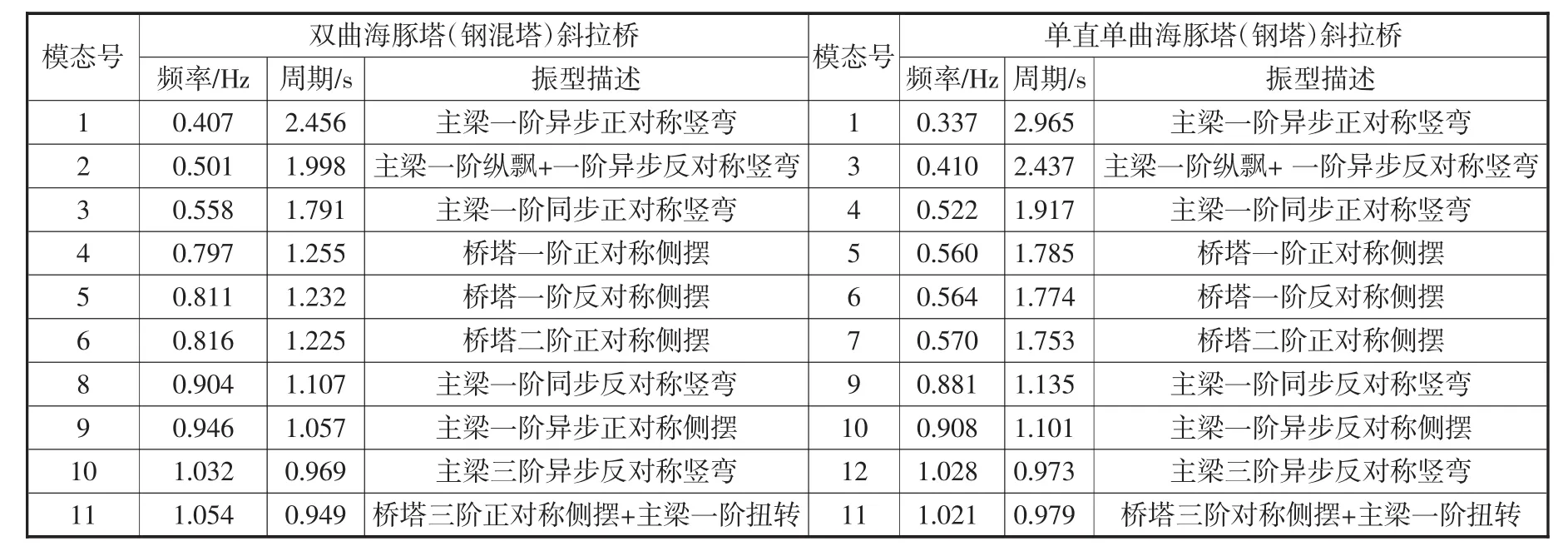
表1 自振频率和模态对比表
在本文中仅给出了双曲海豚塔(钢混结构)斜拉桥的第 1、2、3、8、9、11 阶的自振振型图(图 4)以及主直副曲塔(钢结构)斜拉桥的第 1、3、4、9、10、11阶的自振振型图(图5)。

图4 双曲海豚塔斜拉桥振型图


图5 主直副曲海豚塔斜拉桥振型图
通过对表1、图4、图5进行分析可以得到以下的几点结论:
a)上述两种海豚塔的斜拉桥,其振型模态大体相同,但相应振型的频率却相差较大。两种索塔形式的基本振型都是一阶异步正对称竖弯,一阶竖弯对斜拉桥的地震作用响应和抗风性能有很大的影响,同时对车辆的行车舒适度来说也是非常重要的。在文中,双曲海豚塔斜拉桥的主梁一阶异步正对称竖弯、一阶异步反对称竖弯、一阶同步正对称竖弯、一阶同步反对称竖弯出现在第1、2、3和8阶模态,频率分别是 0.407 Hz、0.501 Hz、0.558 Hz和 0.904 Hz,与其对应主直副曲海豚塔斜拉桥的主梁一阶异步正对称竖弯、一阶异步反对称竖弯、一阶同步正对称竖弯、一阶同步反对称竖弯出现在第1、3、4和9阶,频率分别为 0.337 Hz、0.410 Hz、0.522 Hz和 0.881 Hz。可以看出两种结构的竖向刚度在一阶异步正对称竖弯、一阶异步反对称竖弯和一阶同步正对称竖弯振型中相差较大,并且双曲海豚塔斜拉桥的竖向刚度较主直副曲海豚塔斜拉桥的大,而在一阶同步反对称竖弯中,两种结构的竖向刚度相近。
b)顺桥向的纵向漂移对主塔顺桥向地震反应的贡献占绝对的优势,双曲、主直副曲海豚塔斜拉桥的纵向漂移分别出现在第2和第3阶模态,其频率分别为0.501 Hz和0.410 Hz,并且耦合主梁的竖弯,振型比较复杂。
c)双曲、主直副曲海豚塔斜拉桥的主梁一阶侧弯分别出现在第9和第10阶模态,其频率分别为0.946 Hz和0.908 Hz,两者相差4.02%,从而表明索塔的形式对主梁侧弯刚度影响不大。
d)文中,双曲海豚塔斜拉桥主塔一阶正对称侧摆(对称横桥向振动)和一阶反对称侧摆(反对称横桥向振动)的振动频率分别为0.797 Hz和0.811 Hz,相对应的主直副曲海豚塔的频率分别为0.560 Hz和0.564 Hz,两者的差别分别为29.7%和30.5%,结论表明双曲海豚塔的横向刚度高,抵抗横向变形能力强。
e)在斜拉桥的颤振中主要的振型就是扭转振型,因此分析斜拉桥的颤振临界风速时,结构一阶扭转频率必须足够重视。扭转频率与颤振临界风速基本上呈线性关系,也就是说扭转频率越高,颤振临界风速也就越大。双曲海豚塔和主直副曲海豚塔斜拉桥两种结构形式的主梁一阶扭转振型均出现在第11阶模态,其频率大小分别为1.054 Hz和1.021 Hz,其振型比较复杂,为主梁扭转耦合桥塔的弯曲。
3 结论
分析结果表明大跨度斜拉桥的刚度较小,自振周期较长,基频较低,相邻的频率相差较小,模态比较密集。
通过对两种不同索塔斜拉桥自振特性的分析对比,发现两种不同索塔结构斜拉桥的振型基本相同;但对于相同的振型,双曲海豚塔斜拉桥的频率比单直单曲海豚塔斜拉桥的大,特别是在低阶模态下,两者差异很大;但在高阶模态下,两者的频率非常接近。
通过动力特性分析可以为结构抗风性能和抗震性能研究提供必要的基础,为结构的合理选型提供基本的资料。若要确定结构的抗风性能和抗震性能,还需进一步进行风洞试验和抗震验算,并应根据试验及计算结果,采取相应的措施进行预防。
