基于小波包能量变化率的斜拉桥损伤识别浅析

辛 晨， 周筱航， 周 彪

(西南交通大学土木工程学院， 四川成都 610031)

基于小波包能量变化率的斜拉桥损伤识别浅析

辛 晨， 周筱航， 周 彪

(西南交通大学土木工程学院， 四川成都 610031)

文章根据小波包变换基本原理，构造了小波包能量变化率指标，并将其应用于斜拉桥主梁的损伤识别中。将信息熵作为代价函数，探讨了不同小波包分解层次与小波基函数在损伤识别中的效果，给出了最优小波基和分解层次的选取方法，并将选定的小波基和分解层次运用于斜拉桥主梁损伤识别。结果表明，Daubechies小波基尤其是高阶Daubechies小波基的识别效果较好，且分解层次越大，识别效果越好，但计算量也会随之增加，因此实际工程中应综合信息熵和计算时间来确定分解层次；小波包能量变化率指标对损伤较为敏感，能够检测出损伤发生的位置。

结构损伤识别； 斜拉桥； 信息熵； 小波包能量变化率； 小波基函数

损伤识别是结构健康监测的重要内容，最早在航空航天工程、机械工程等领域得以运用，近年来越来越多的学者将其应用于复杂化、大型化的土木工程领域。结构的损伤识别旨在判定结构是否有损伤、损伤的位置、损伤的程度以及对结构的剩余寿命进行评估。在众多结构损伤识别方法中，小波分析因其优越的时频域分析能力得到了许多成功的应用。

小波分析的基本思想沿承了Fourier变换，就是将信号在一系列基函数张成的空间上进行投影。小波变换是一个时间和频率的局域变换，因而能有效地从信号中提取信息，通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析。Deng[1]等对钢梁施加冲击荷载，对采集的信号进行小波变换，识别出了冲击荷载作用的时间和位置。Liew[2]等通过建立带裂缝梁峰结构模型，推导出了结构力学变量的小波方程，将模型动力响应信号进行离散小波变换，从小波细节系数的突变来定位裂缝。Hou[3]等利用Daubechies小波对结构动力模型加速度相应进行了小波变换，从信号奇异点识别出结构损伤，并认为基于小波的损伤识别技术能很好地用于结构的实时监测。任宜春[4]等利用小波包分解得到的特征能量向量作为损伤指标，对一钢筋混凝土梁进行了损伤测试诊断。Sun[5]等以一连续梁为模型，利用小波包分解信号的能量来建立损伤指标，结合神经网络对连续梁的损伤进行了识别，并分析了测量噪声对识别结果的影响，结果表明识别效果较好。朱劲松和孙雅丹[6]等提出了小波包能量变化率平方和损伤指标，对简支梁模型进行数值模拟分析，针对单一损伤与两处损伤时不同损伤程度的情况，证明了该指标的有效性。

小波分析在结构损伤识别领域得到广泛的应用，但如何选取小波基函数和小波包分解层次，目前尚未有统一的理论准则[7]。实际研究中，选择合理的小波基和小波包分解层次，对结构损伤识别具有重要的意义。

本文对一座双塔双索面曲线斜拉桥的有限元模型进行主梁的损伤识别，通过动力时程分析得到主梁各节点的加速度响应值。将通信学中的信息熵作为代价函数，分别以不同小波基函数和不同分解层次求得主梁上某一节点的信号能量，综合计算时间，给出了最优小波基和最合适分解层次的选取方法，并将其应用于斜拉桥主梁损伤位置识别中。

1 小波包能量法的基本原理

结构发生损伤时，其动力响应信号的某些频段会发生一定的波动，导致小波包分解的信号分量中某一个或多个分量的能量发生变化。本文将小波包能量变化率作为结构损伤识别的判断指标。从数学角度来讲，数字信号f(t)的能量就是其各点幅度值的平方和。小波包分解能够对信号的低频部分和高频部分均进行分解，将信息无冗余、无疏漏并且正交地分解到各个子频带，因此，原始信号的总能量应为各子空间能量之和。

结构动力响应f(t)经过j水平的小波包分解后可表示为：

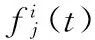
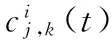
定义在j水平下的信号能量Ef为：

再考虑到小波包函数的正交特性，信号的总能量可认为是由不同频带内小波包组分能量的总和：

小波包能量变化率指标对于信号变化特征相对敏感，且能够通过具体数值判断损伤出现的位置，因此采用该指标来进行损伤识别。

2 斜拉桥主梁损伤识别

2.1 数值模拟

本文以刚果布拉柴维尔大桥试验模型桥为研究对象进行损伤识别。模型桥为双塔双索面曲线斜拉桥，桥跨形式为2.4125 m+4.05 m+14.25 m+4.05 m+2.4125 m=27.175 m。模型桥塔为菱形，采用钢材制作。主梁上设置1.987 %的纵坡，因此各墩高度略有变化，桥墩为门式，主梁采用Q235钢板制作且设置有厚度为10 mm的横隔板，并分为普通梁截面和加宽梁截面。全桥共有120根斜拉索，采用碳素弹簧钢丝模拟，拉索直径有三种，分别为3.5 mm、4 mm、5 mm(图1)。

精神分裂症主要指个性、情感以及思维等方面出现异常，临床主要表现为精神活动与周围环境协调性差，其中青壮年是高发人群[5]，极大影响了患者的身体健康以及生活质量，同时也给社会带来较大的负担。首发精神分裂症往往起病缓慢，发病早期较难引起患者及其家属的重视，若治疗、护理不及时，则会造成病情不可逆性恶化[6]。

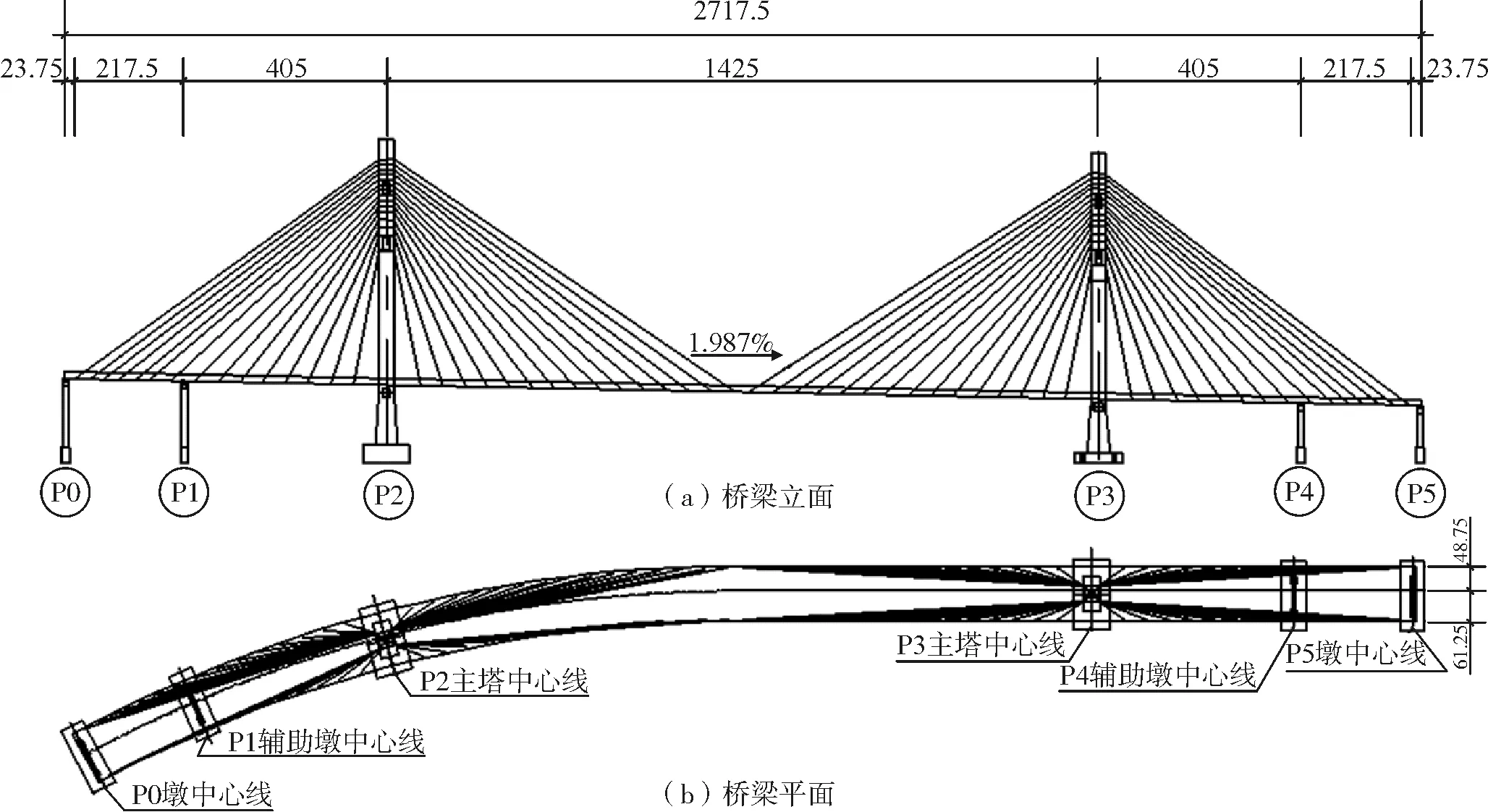
图1 试验模型桥总体布置(单位：cm)

用大型有限元软件Midas Civil2015建立了试验模型桥的有限元数值分析模型，以单元刚度折减来模拟主梁损伤工况，对有限元模型进行瞬态动力响应分析，在Midas时程分析中选择1940年EI Centro Site地震波作为输入的激励荷载，得到相应节点处的加速度信号。图2中□表示待损伤单元，其中1、5单元位于边跨跨中，2、3、4单元位于中跨四分点处。图2中●表示待提取加速度信号的节点，其中1、2和10、11号节点分别位于边跨跨中，3～9号节点分别位于中跨八分点处。

图2 损伤模拟示意

2.2 小波基函数和分解层次的选取条件

在进行小波包分析时，小波基函数并不是唯一的，所有满足小波条件的函数都可以作为小波函数。随着小波理论及各种数值方法的发展，越来越多的小波基函数得到了广泛的应用，而根据小波基函数的不同，小波包变换的结果也不尽相同。常用的小波基函数有Haar小波、Daubechies(dbN)小波系、双正交小波Biorthogonal(biorNr.Nd)小波系、Coiflet(coifN)小波系、SymletsA(symN)小波系、Morlet(morl)小波、Meyer函数等等。选择小波基函数时应综合考虑以下几个因素。

2.2.1 支撑长度

对于函数f(x)，如果自变量x在0附近的取值范围内，f(x)能取到值；而在此之外，f(x)取值为0，那么这个函数就是紧支撑函数，具有该性质的小波成为紧支撑小波。如果当自变量x→∞时，函数快速衰减或具有指数规律衰减，那么这个函数就是急衰或急降的。紧支撑性和衰减性是小波的重要性质，但一个函数无法满足在时域和频域内同时紧支，最多一个是紧支的，一个是急衰的。一般希望小波函数能在时域上具有紧支撑性，且紧支撑特性越明显，其检测奇异信号的能力越强。

2.2.2 消失矩阶数

消失矩表明了小波变换后能量的集中程度，用消失矩大的小波函数分析突变信号时，能更有效地检测出奇异点。但一般情况下，消失矩越高就意味着支撑长度越长，所以二者需权衡折中处理。

2.2.3 正则性

小波函数的正则性就是其光滑程度的一种描述，也是其频域能量集中的一种度量，正则性阶数越大，意味着函数越光滑，其频域的能量就越集中。正则性可表现为小波函数的可微性，这对于在小波变换中有效地发现信号奇异点是必要的。对大部分正交小波函数而言，正则性越高，其消失矩也就越高。另外，正则性也与支撑长度有关，支撑长度越大，正则性就越好。因此，实际应用中往往选择正则性较大的小波函数。

2.2.4 对称性

对称性对小波函数而言是非常重要的，具有对称性的小波函数可用来构造紧支的正则小波基，而且具有线性相位。Daubechies证明除了Haar小波基，不存在对称的紧支正交小波基。但对于双正交小波基，可以合成具有对称或反对称的紧支小波基。

2.2.5 正交性

实际应用中，我们往往希望小波基函数是有限支集且是对称或反对称的，但除了Haar小波外，紧支集的小波一般都不具有对称性。因此可放松对正交性的要求而采用双正交小波基。

表1为常用小波基的主要性质。

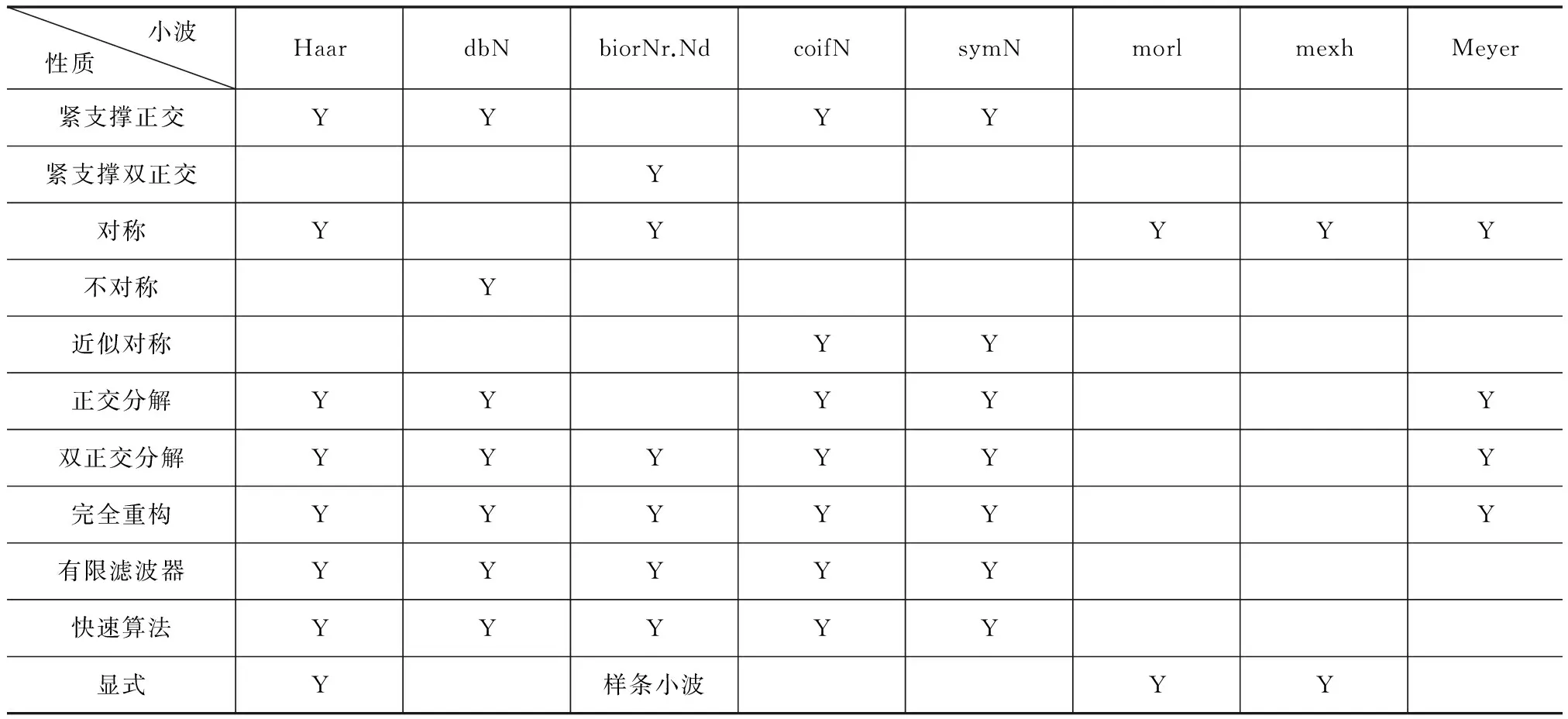
表 1 常用小波基的主要性质

注：Y表示小波基具有此性质，空白表示不具有此性质。

综合考虑上述性质，本文重点考察采用Daubechies和SymletsA小波的损伤识别效果。Daubechies小波是离散正交小波，一般写作dbN，N为小波的阶数。SymletsA小波是近似对称的小波函数，它是对db函数的一种改进，通常写作symN的形式。对于dbN小波来说，N的取值理论上没有上限，当N=1时，dbN小波就是Haar小波；对于symN小波来说，N最大可取为8。

2.3 最优小波基和分解层次的选取

信号的小波包分解实质上就是信号在小波基函数上的投影，从而可求得一系列用来表达原始信号特性的系数。当这些系数差别很大时，那么仅用少数系数就可以完整地刻画原始信号的特性，显然这样的小波基是最优小波基；当这些系数彼此接近时，就难以刻画原始信号的特性，与之相对应的小波基就不是最优小波基。

通过刻画这些系数的性质来评定小波基函数的优劣，需要定义一个代价函数M，使得M在小波包系数序列u={uk}上满足：

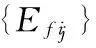
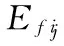
将分解层次取为3～7，小波基选择db15、db20、db25、db30、db35和sym2、sym4、sym6、sym8。分析时，先确定小波包分解层次，计算并比较不同阶次小波基函数的代价函数，通过比较代价函数值确定小波基函数。确定小波基函数后，再用相同的方法，分析比较选择合适的分解层次。选择出最优小波基和合适的分解层次后，即可对结构动力响应信号实施小波包分解。

以完好工况下5号节点测得的时程信号为例。首先确定分解层次为7，利用不同小波基函数对信号进行小波包分解，计算信息熵，结果见表2。

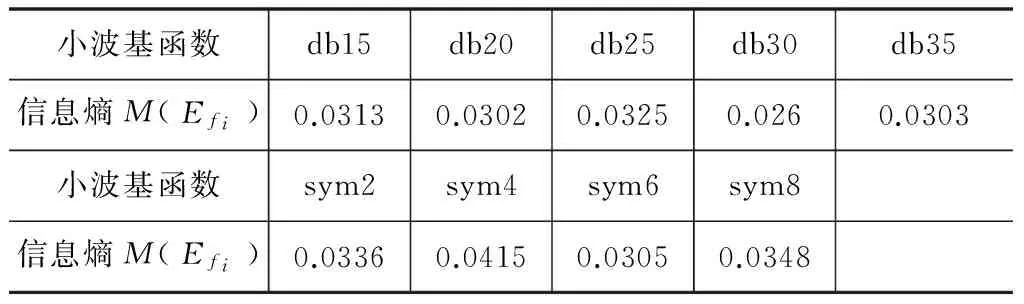
表 2 不同小波基函数的信息熵

由表2可知，当小波基函数选为db30时，信息熵值仅为0.026，相对其他结果较小，因而小波基函数可选为db30。确定小波基函数后，分解层次取3～7。

由于信号经第j层小波包分解后，有2j个子频带，因此随着分解层次增加，计算负担也会加重。因此，在确定小波基函数后，分解层次取3～7，计算不同分解层次下的信息熵值并记录计算时间，结果见表3。

表 3 不同分解层次的信息熵

由表3可知，当分解层次为8时，代价函数值为0.0152，计算时间为1 s，两个参数相对其他分解水平均较小，因此，后文采用分解层次为8的db30小波基函数对信号进行小波包分解。

2.4 主梁损伤位置的识别

在进行主梁损伤位置识别过程中，理论上需要对斜拉桥主梁全部节点进行加速度响应测试，通过小波包变换求得每个节点处的损伤指标，从而准确地进行损伤识别。这就意味着实际应用中需要大量的传感器，无论从经济性还是实际操作来讲都是很难实现的，因此本文选用上一节提到过的11个节点进行损伤识别。

用小波包能量变化率指标计算这11个节点在不同损伤工况下的值，并将节点编号和损伤指标值绘成柱状图。本文选择两种损伤工况，分别为1号单元损伤和2号单元损伤，损伤程度均为50 %(图3)。

(a) 1号单元损伤

(b) 2号单元损伤图3 损伤指标

从图3中可看出，1号单元损伤情况下，2号节点处的指标值较其他节点发生了明显的变化，即损伤可能发生在2号节点附近，在有限元模型中2号节点与1号单元最为接近，理论上1号单元发生损伤时2号节点的损伤指标值应最大，因此识别效果较好。2号单元损伤情况下，4号节点的指标值最为突出，理论上2号单元发生损伤时4号节点的指标值应最大，因此识别效果较好。

3 结束语

小波包分析时所采用的分解层次和小波基函数具有多样性，不同的选择会产生不同的结果，因此，选择最优分解层次和最优小波基是小波包能量法应用于结构损伤识别中的一个关键问题。本文介绍了小波基函数选取时需要考虑的因素，采用双塔斜拉桥模型桥有限元模型数据，通过定义信息熵为代价函数，考察了不同小波基和分解层次的损伤识别效果并选出了最优小波基和分解层次。以小波包能量变化率为损伤指标，成功对数值模型桥主梁进行了损伤位置的识别。得到如下结论：

(1)以信息熵作为代价函数来选取最优小波基和分解层次，可通过具体数值进行判理论上小波基函数的阶次越大越好，分解层次也越高越好，本文通过信息熵最终选择db30小波基，再综合计算时间将分解层次取为8，说明以信息熵作为代价函数的方法可行。

(2)将选择的小波基和分解层次应用于斜拉桥主梁损伤位置的识别，以小波包能量变化率为损伤指标，可以很好地判断出损伤的位置，说明小波包能量变化率指标对损伤较为敏感。

[1] Deng X, Wang Q, Giurgiutiu V. Structural health monitoring using active sensors and wavelet transforms[A]. Proc. SPIE[C]. Newport beach, 3668:363-370.

[2] Liew K.M, Wang Q. Application of Wavelet Theory for Crack Identification in Structures[J]. Journal of Engineering Mechanics, 2014, 124(2):152-157.

[3] Hou Z.K. etc.. Wavelet-based approach for structural damage detection. Journal of EM, ASCE, Vol.126(7),2000:677-683.

[4] 任宜春，张杰峰，刘哲峰. 钢筋混凝土梁损伤的小波包识别方法[J]. 震动、测试与诊断，2011，31(5)：605-609.

[5] Sun Zhi, Chang Chih-Chen, Wavelet packer signature: A novel structural condition index, China-Japan Worksho P in Vibration Control and Monitoring of Structure and Third Chinese Symposium on Structure Vibration Control, Shanghai, China, Dec, 2002:1-10.

[6] 朱劲松，孙雅丹. 基于小波包能量的桥梁损伤识别指标[J]. 振动、测试与诊断，2015，35(4):715-721.

[7] 丁幼亮，李爱群，邓扬. 面向结构损伤预警的小波包能量谱识别参数[J]. 东南大学学报： 自然科学版，2011，41(4):824-828.

U441+.4

A

[定稿日期]2017-05-11

中国路桥集团重大科技项目(编号：2014C008)

辛晨(1993～)，男，硕士研究生，研究方向为结构健康监测；周筱航，男，博士研究生，研究方向为结构健康监测与施工控制。