图形中的有趣规律

◎ 邵子坤

图形中的有趣规律

◎ 邵子坤

对于一些较复杂或数目较大的问题，如果一时感到无从下手，我们不妨把问题尽量简单化，在不改变问题性质的前提下，考虑最简单的情况（化大为小），从中分析探寻出问题的规律，以获得问题的答案。这就是解数学题常用的一种方法，我们不妨称之为“化大为小找规律”。

例1：如果在一条直线上做出35个点，这些点将把直线分为多少个部分？如果有n个点呢？

思路点睛：如果你想在一条直线上画出35个点，再数出直线一共被分成了多少个部分，当然是可以的，但是，这样做显然比较麻烦。换个思路，先从简单的情形想起，看看能不能从中找到规律。

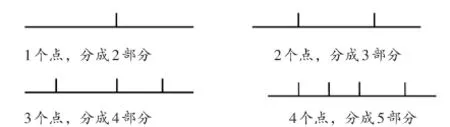
不难发现，这条直线被分成的部分数应该比点数多1。可见，35个点将把这条直线分成35+1=36个部分；而n个点将把这条直线分成n+1个部分。

例2：下面的每个图形都是由边长1厘米的小正方形拼成的。照这样排列的第n个图形中，阴影正方形和非阴影正方形的个数各可以怎样表示？

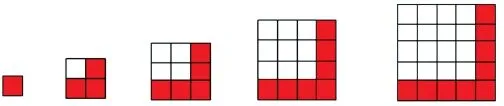
为了便于发现规律，我们不妨列个表试试：

从表中很容易看出，阴影正方形的个数按1、3、5、7、9……这样的规律排列，那么第n个图形中，阴影正方形的个数可以表示为2n-1。而非阴影正方形的个数是按0、1、4、9、16……的规律排列的，第n个图形中，非阴影正方形的个数可表示为（n-1）2。

你还能发现什么规律呢？