径流及盐度对瓯江口滞留时间影响的数值模拟研究
2017-11-09聂学富
聂学富
(滁州学院 后勤管理与基建处,安徽 滁州 239000)
径流及盐度对瓯江口滞留时间影响的数值模拟研究
聂学富
(滁州学院 后勤管理与基建处,安徽 滁州 239000)
采用动边界改进的ECOMSED模式对瓯江口滞留时间对于径流及盐度密度流的响应进行了数值模拟研究,并对淡水比率法、潮棱体模型以及修正的潮棱体模型等多个方法进行了对比研究.研究认为,瓯江口滞留时间随径流量的增加而减小,二者呈现较好的函数关系.瓯江口盐度对瓯江口存在重要影响,但盐度对滞留时间的影响相对径流而言较小.相同的径流量在考虑盐度和不考虑盐度的情况下冲刷率不同,不考虑盐度时的冲刷率略小于考虑盐度时的情况.
瓯江;滞留时间;ECOMSED;盐度
1 相关研究现状
河口是海洋与河流的交汇段,兼具河流和海洋的某些特征.河口水体受到淡水上游径流及涨潮海水进入的双重影响,由于密度的差异、径流、潮汐和地形的作用,盐水和淡水发生混合.同时,河口是盐水和淡水的交汇地带,河口出现的多种物理、化学、生物过程,如河口环流、细粒泥沙絮凝沉降、最大浑浊带等都与盐水入侵密切相关,盐水入侵及其进一步恶化[1].河口物质输运时间尺度是将河口物理过程与生态过程联系起来的一个重要指标,越来越引起人们的关注.输运时间尺度经常与生物化学过程的时间尺度进行比较以量化水动力过程在污染物输入及演化过程中的重要性.以滞留时间为例,如果滞留时间小于河口内生物化学过程的时间或二者基本相当,即可认为河道内的物质基本上可以排出;相反,如果滞留时间大于生物化学过程的时间尺度,则有理由认为河口内的生态环境是易受到负面影响的.瓯江下游是我国重要的经济区,该地区经济高速发展的同时环境保护问题也日益凸显.因此,为有效控制瓯江口海洋环境的污染以及对海洋的其它合法利用,开展瓯江口输运过程及物质交换的时间尺度的研究具有现实和长远的意义.
滞留时间可以将河口生态系统研究的许多方面统一起来,它反映了水动力过程和生态过程间最根本的联系.滞留时间是水体微团或其它要素如盐、污染物等从其进入某一水体至被输运到水体以外滞留在水体中的平均时间,在稳态条件下,可以根据河口内某变量与其在边界处的交换速率的比值来估算.由于空间差异和河流过程的时间依赖性及许多重要物质的非线性行为,使得滞留时间十分复杂[2-3],所以仅了解滞留时间的平均值是不够的,还应考虑它的时空变化等特征.Awaji and Signell等使用水体示踪法对潮汐交换机理进行了有益的探讨[4-6].漂流物示踪技术的进步为记录河口拉格朗日运动和交换提供了前所未有的机会.随着采样技术的发展,精确的示踪物将为流体交换过程提供了更精确的信息[7].数学模型的优化和更全面的验证使得模型方法成为评价河口净化速率的重要途径.Zimmerman[3]给出的滞留时间的定义为:水体中某一个物质微团的滞留时间为它在到达水体的出口前在水体中的停留时间.可以看出,滞留时间也是时间和空间要素的函数.不同空间位置的物质微团在不同时刻排放将会导致其在水体中具有不同的滞留时间.Takeoka[8]给出的滞留时间的定义和计算方法,为通过数学模型手段研究滞留时间问题奠定了基础.随着河口环境问题越来越引起重视,河口输运的时间尺度方面的研究在近几年也取得了很大进展[9-12].SWAT模型在国外的应用非常广泛,近几年来,在国内也逐步被推广起来,很多研究者开始应用SWAT模型[13].鉴于理论适用性和运用性,本文将利用改进的ECOMSED模式对径流、盐度对瓯江口滞留时间的影响进行研究.
2 瓯江口数值模拟及滞留时间计算
ECOMSED是一个比较全面的河口海岸数学模型,但ECOMSED无动边界处理.作为一个河口海岸模型,固定岸边界的处理方式对于浅滩及附近的海域可能导致相当的误差甚至不能进行模拟,需要进行相应的改进.本文动边界的处理采用干湿网格法.数值试验表明,该方法推广至三维海洋模型中,能够取得预期的效果[14].在盐度等变量的计算中,由于干湿网格法的引入,可能导致在落潮过程中湿变干的网格的周围的网格连续方程得不到满足,虽然这种误差是微小的,并不对水动力方程的求解带来本质的影响,但是这种误差对于盐度等标量计算的影响是必须考虑的.对于干变湿网格的前一时刻的值,Oey Li[15]在研究中采用了背景值的处理方法,但事实上,背景值是很难准确获得的.所以本文将采用与该点水位一样的处理方法,即采用其周围湿点的平均值.为了适应复杂地形,涨潮时干变湿的最小水深略大于落潮时最小水深.
将改进后的ECOMSED模式应用于瓯江口及其邻近海域(见图1).数学模型的计算范围上游边界位于瓯江干流圩仁站附近,采用流量控制,外海边界取在飞云江口~南麂~坎门一线,边界给定潮位过程.计算采用曲线正交网格总共包括230×236个网格,网格步长为20~1 000 m.模型采用的地形数据梅岙以下为2005年6月的实测数据.验证资料为2005年6~7月的同步测量水文资料,垂向分7层,盐度的边界条件上游取为零,下游表层取31、底层取33,初始条件由实测数据插值得到.滞留时间计算过程中,河口内污染物质的输运采用改进的原模式中TRACE模块,并在模式中加入滞留时间的计算,滞留时间的计算方法采用Takeoka方法[8].经验证模型能够复演瓯江口水动力即物质输运过程.
2.1 计算方案
滞留时间的研究区域为梅岙以下至河口口门的整个河段,南口不考虑物质的排放,积分区域上游梅岙至下游的南、北口口门.模型控制条件上游径流量分别取Q80、Q50、Qm、Q20及Q5,外海边界取大、中、小潮的混合形式.
2.2 计算结果分析
河口是径流淡水与海水的过渡区域,水动力状况复杂,盐度梯度对河口混合及物质输运有重要影响.图2和图3分别给出了不考虑盐度和考虑盐度情况下瓯江口滞留时间与径流量的关系.可以看出瓯江河口的滞留时间随着流量的增加而减小.不考虑盐度的情况时,Q80流量下滞留时间约为106 h,Q50流量下滞留时间约为88 h,Qm流量下滞留时间约为72 h,Q20流量下滞留时间约为67 h,Q5流量下滞留时间约为45 h.考虑盐度的情况时Q80流量下滞留时间约为96.3 h,Q50流量下滞留时间约为80.4 h,Qm流量下滞留时间约为64.4 h,Q20流量下滞留时间约为61.6 h,Q5流量下滞留时间约为43 h.从图2与图3中分别对数据点进行了幂函数及对数函数拟合.可以看出,滞留时间与流量呈现良好的函数关系,定义参数:

图1 瓯江河口地形
(1)
式(1)中,Rtimef和Rtimes分别为不考虑盐度及考虑盐度的情况的滞留时间.图4为R随流量的变化.可以看出R的值恒小于1,其平均值约为0.9,并随着流量的增加而增大.
表1统计了瓯江河口有、无盐度影响下的滞留时间、冲刷率、盐度和径流的影响.总体看来,瓯江河口的滞留时间呈现随着流量的增加而逐渐减小的变化趋势.在正压情况下,上游流量为0 m3/s时,滞留时间为118.4 h,冲刷率为0.008 4 kg/h;而在考虑盐度的情况下,相应的滞留时间为108.3 h,冲刷率为0.009 2 kg/h.此二数值代表了仅潮汐动力因素的冲刷作用,可以看出盐度导致的密度变化使潮流的冲刷率有一定的增大.将上游流量取Q80、Q50、Qm、Q20和Q5时的冲刷率分别减去流量取为0情况下的冲刷率,所得结果可以认为是不同的径流量的对于冲刷率的影响.分别列于表1的第6列和第7列.可以看出,在考虑盐度情况下,在上游径流分别取量Q80、Q50、Qm、Q20和Q5时,相对于潮流的单一影响(上游径流量取0 m3/s)冲刷率分别增加0.001 2 kg/h、0.003 2 kg/h、0.006 1 kg/h、0.007 kg/h和0.014 0 kg/h.在不考虑盐度作用的情况下相应值分别为0.001 1 kg/h、0.003 0 kg/h、0.005 6 kg/h、0.006 5 kg/h和0.014 0 kg/h.图5给出了径流的冲刷率随径流量大小的变化情况.图中显示冲刷率随着流量的增加而增大.不论是考虑盐度的斜压情况还是不考虑盐度影响的正压情况下,径流的冲刷率的变化均与上游流量呈现极好的规律性.图中对两种情况的数据给出了线性函数拟合,可以看出R2均超过了0.99.图中的两条横线分别为冲刷率取0.008 4 kg/h和0.009 2 kg/h,代表了考虑盐度和不考虑盐度情况下的仅潮流作用的冲刷率.二者与前述的拟合线相交.在不考虑盐度影响的情况下,交点(A)位于Q≈720 m3/s处,说明当不考虑盐度的潮流冲刷率与上游来水为Q≈720 m3/s的径流冲刷率相当.而交点(B)说明在考虑盐度的情况下,潮流的冲刷作用与径流量为Q≈750 m3/s的冲刷率相当.图中的另两个交点(C)和(D)分别位于Q≈690 m3/s和Q≈800 m3/s位置.C点说明690 m3/s的上游径流来水在考虑盐度因素情况时的冲刷率即可以达到不考虑盐度的单纯潮流冲刷作用.而D点则表明的是若要达到盐度因素作用下的潮流的能力,在不考虑盐度时需要的上游流量为Q≈800 m3/s.相同的径流量在考虑盐度和不考虑盐度的情况下,其冲刷率是不同的.不考虑盐度时的冲刷率略小于考虑盐度时的情况.

图2 滞留时间与径流量的关系1(左:正压;右:斜压)

图3 滞留时间与径流量的关系2(左:正压;右:斜压)

图4 R随径流量的变化

图5 冲刷率与流量的关系
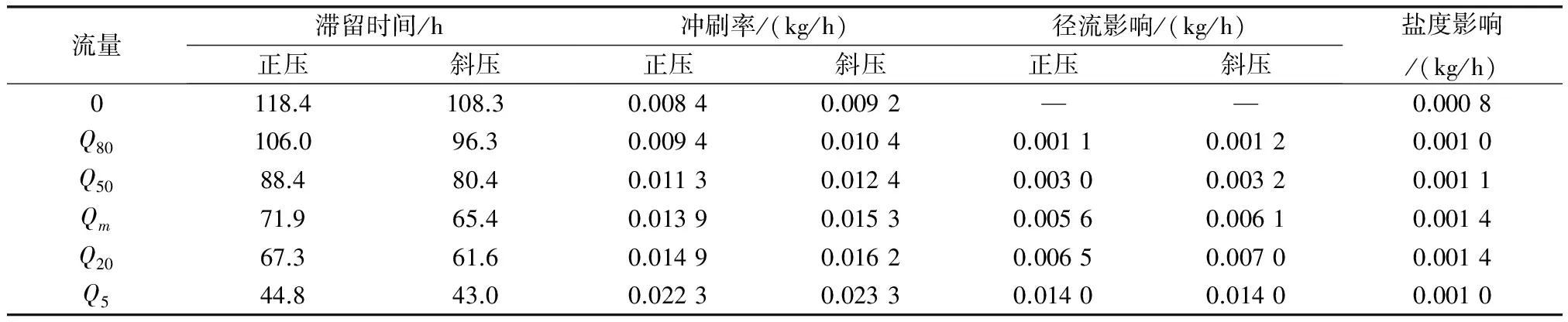
流量滞留时间/h正压斜压冲刷率/(kg/h)正压斜压径流影响/(kg/h)正压斜压盐度影响/(kg/h)0118.4108.30.00840.0092——0.0008Q80106.096.30.00940.01040.00110.00120.0010Q5088.480.40.01130.01240.00300.00320.0011Qm71.965.40.01390.01530.00560.00610.0014Q2067.361.60.01490.01620.00650.00700.0014Q544.843.00.02230.02330.01400.01400.0010
导致河口重力环流的压强梯度力包括正压和斜压两部分.落潮过程中,这两个压力场方向相反,表层正压力大于斜压力,而在底层则表现为斜压力大于正压力,二者之和在表层指向口外,而在底层则指向上游.在涨潮阶段,正压力和斜压力均指向上游,但相对于其垂向平均值,仍表现为表层指向外海,而底层指向上游.在整个潮周期的平均结果来看,底层压强梯度力指向上游,维持一个向上游的余流,而表层则相反,维持一个向海的余流.图6、图7分别给出了正压和斜压情况下瓯江口内表层和底层的欧拉余流场.可以看出,在正压情况下瓯江河口的余流不论表层与底层均指向口外,这一结果与理论解是一致的.盐度的影响导致底层余流方向改变为指向上游,表层余流指向口外.不考虑盐度的影响下,整个水体可以认为不存在密度差异.考虑盐水的影响的情况下,盐度将导致密度梯度的出现.另一方面,垂向上来看,深槽中的余流总体至向口外.盐度导致的密度差异有利于河口重力环流的产生和发展,从而有利于口内污染物的向外海的输运,导致河口滞留时间的减小.

图6 欧拉余流(正压;上:底层;下:表层)

图7 欧拉余流 (斜压;上:底层;下:表层)
对于水库或非潮汐河口,水流是单向的,甚至可以近似为定常的,水流结构相对简单,其水体交换的时间尺度的计算也相对容易.而对于潮汐河口,传统的潮棱体方法或淡水组分法等有可能导致较大的误差,采用修正的潮棱体方法计算河口滞留时间涉及到的一个关键的因素:回流系数.Sanford[16]等在其研究中将回流系数定义为落潮时流出河口、在涨潮时又返回河口的水体占整个涨潮水体的体积比.由于随落潮流挟带至口门外的水体中的部分污染物质在下一个涨潮过程中会随涨潮流重新进入河口内,进而影响河口内污染物向口外输运的平均时间,所以在滞留时间计算过程中,由于这部分物质的参与,考虑回流的影响是必须的.在计算小型河口或海湾的输运时间时应结合实际选取相应的回流系数(b)的值.Sanford等指出,b是3个长度因子(羽流扩散宽度、羽流中心线离岸距离、扩散特征长度)和1个时间因子(潮周期)的函数.一般可认为取值在0~0.5之间.也有文献将b值当作一个常量(b=0.5)来处理.Wang C.F.的研究中b值是通过率定的方法选取,将径流量为0情况下某滞留时间计算方法(如Takeoka法)所得的计算值作为参考以确定b的取值.在理想河口情况下,考虑物质输运的对流输运和扩散输运两种机制,本文将回流系数通过下式计算.

(2)
式(2)中,α为系数,取0.5;Vflood和Vebb分别为涨潮及落潮过程中通过口门的潮量.采用潮棱体方法或修正的潮棱体方法以及淡水比率法计算的瓯江河口的滞留时间及冲刷时间(见表2),可以看出采用淡水组分法计算的冲刷时间与其它方法计算的滞留时间有较大差距.冲刷时间随径流量的变化在大径流量变化较小,而在低流量时变化幅度很大.这是由于其计算公式中以径流量做分母所决定的.另一方面,淡水组分法所计算的冲刷时间远大于其它方法所得的滞留时间,主要有两方面的原因:一是在冲刷时间的计算中未考虑潮流的冲刷作用;二是因为冲刷时间与滞留时间的定义存在着差异.冲刷时间是将河口水体中的污染物质全部冲刷掉所需要的时间,而滞留时间依照定义则为污染物在水体中停留的平均时间.所以可以认为,对于瓯江这样的强潮河口,由于潮汐动力很强,淡水组分法不适用.由表2列出的通过潮棱体方法计算的瓯江口的滞留时间可以看出,滞留时间基本不随上游径流量的变化而变化,各流量下均约为43 h.其原因是在此方法滞留时间的计算未考虑上游径流的影响,由其计算公式中也可以看出径流的因素并未体现.另一方面,瓯江口属强潮河口,潮棱体巨大,径流量对潮棱体的影响较小,所以各流量下的值相差不大.另外,在此方法中回流因素同样未考虑,所以采用潮棱体方法计算的滞留时间与其它方法(Takeoka法、Luketina法)相比均偏小.表2给出了Luketina法计算的滞留时间,回流系数的确定方法分别为通过式(2)、率定法和0.5.可以看出,总体而言相对于应用Takeoka方法的数学模型计算值,由于考虑了潮汐的因素采用式(2)得出的回流系数计算的滞留时间的误差较采用率定法或取常值0.5的情况要略有减小,但是最大误差仍接近30%.所以可以认为,由于天然河口情况的复杂性以及潮棱体方法、修正的潮棱体方法、淡水比率法等简单模型自身过多的假设,计算误差一般比较大.

表2 瓯江口滞留时间与冲刷时间
注:表中带*代表率定值.
3 结 语
通过采用干湿网格法改进的ECOMSED模式研究了径流及盐度对瓯江口滞留时间的影响规律,并将淡水比率法、潮棱体模型以及修正的潮棱体模型等方法应用于瓯江口进行了对比研究.研究认为,瓯江口盐度密度流对瓯江口存在重要影响.瓯江口滞留时间随径流量的增加而减小,二者呈现较好的函数关系.盐度对滞留时间的影响变幅在10 h左右.相同的径流量在考虑盐度和不考虑盐度的情况下冲刷率不同,不考虑盐度时的冲刷率略小于考虑盐度时的情况.河口内污染物主要经由深槽向外海运移.对潮棱体模型等方法进行的对比研究显示,由于过多假设和简化,淡水比率法、潮棱体模型以及修正的潮棱体模型用于情况复杂河口效果不理想.
[1] 章 洁,卢 勇,张红武.钱塘江河口盐度入侵二维数值模拟研究[J].浙江水利水电学院学报,2016,28(4):14-18.
[2] OLIVERIA A., A. M. BAPTISTA. Diagnostic modeling of residence time in estuaries[J]. Water Resources Research,1997(33):1935-1946.
[3] ZIMMERMAN J. T. F., Estuarine residence times. In: Kjerfve, B. (Ed.), Hydrodynamics of Estuaries 1, Estuarine Physics. CRC Press, Inc., Boca Raton, Florida,1988:76-84.
[4] AWAJI T., N. IMASATO, H. KUNISHI. Tidal Exchange through a Strait: A Numerical Experiment Using a Simple Model Basin[J]. Journal of Physical Oceanography,1980,10(10):1499-1508.
[5] SIGNELL R. P., W. R. GEYER. Numerical simulation of tidal dispersion around a coastal headland, Residual currents and long-term transport [J]. Coastal and Estuaries Series,1990:210-222.
[6] SIGNELL R. P., Butman. Modeling tidal exchange and dispersion in Boston harbor[J].JGR:1992(97):1591-1606.
[7] HITCHCOCK G.L., D. B. OLSON. A GPS-tracked surface drifter with cellular telemetry capabilities[J]. Marine Technology Society Journal,1996(30):40-49.
[8] TAKEOKA H., Fundamental concepts of exchange and transport time scales in a coastal sea[J]. Continental Shelf Research 1984,3(3),322-326.
[9] SHEN J., LIN J., Modeling study of the influences of tide and stratification on age of water in tidal James River. Estuarine[J]. Coastal and Shelf Science,2006(68):101-112.
[10] DELHEZ E.J.M., Heemink.Residence time in a semi-enclosed domain from the solution of an adjoint problem[J]. Estuarine, Coastal and Shelf Science,2004(61):691-702.
[11] SHELDON J.E., ALBER M., A comparison of residence time calculations using simple compartment models of the Altamaha River estuary, Georgia[J]. Estuaries,2002,25(6B):1304-1317.
[12] HILTON A.B., MCGILLIVARY D.L. Residence time of freshwater in Boston’s inner harbor. Journal of Waterway[J]. Port, Coastal, and Ocean Engineering,1997,124(2):82-89.
[13] 张徐杰,朱 聪,程开宇,等.SWAT模型在兰州江流域未来径流模拟中的应用[J].浙江水利水电学院学报,2016,28(2):13-16.
[14] 陈长胜.海洋生态系统动力学与模型[M].北京:高等教育出版社,2005.
[15] OEY LI. An OGCM with movable land-sea boundaries[J]. Ocean Modeling,2006(13):176-195.
[16] SANFORD L.P., BOICOURT W.C., RIVES S.R..Model for estimating tidal flushing of small embayments[J]. ASCE Journal of Waterway,Port, Coastal and Ocean Engineering,1992,118(6):635-654.
[17] WANG C.F., HSU M.H., KUO A.Y.. Residence time of the Danshuei River estuary, Taiwan. Estuarine[J]. Coastal and Shelf Science,2004(60):381-393.
NumericalSimulationonInfluenceofRiverDischargeandSalinityinResidenceTimeinOujiangEstuary
NIE Xue-fu
(Logistics Management and Infrastructure Department, Chuzhu University, Chuzhou 239000, China)
ECOMSED modified by Wet/Dry moving boundary method was applied in the Oujiang estuary to investigate the influence of river discharge and salinity in residence time. Numerical simulations show that the residence time is mainly affected by river discharge. The residence time increases as the fresh flow decreases. The variety of residence time due to salinity-induced density circulation is relatively small. The same river flow results in larger flushing rate under baroclinic conditions than barotropic conditions. Comparative researches exhibit that because of significant assumptions and implications, simple prism model, revised prism model and fresh water rate method can not give satisfied estimates in complex estuaries
Oujiang estuary; residence time; ECOMSED; salinity-induced circulation
10.3969/j.issn.2095-7092.2017.04.003
TV131
A
1008-536X(2017)04-0012-08
2017-04-20
聂学富(1979-),男,安徽六安人,硕士,工程师,研究方向为项目管理.
