基于能量法的船用气囊爆炸模型及破坏研究

赵殿华，段青灵

（山东南海气囊工程有限公司，山东 济南 250101）

基于能量法的船用气囊爆炸模型及破坏研究

赵殿华，段青灵

（山东南海气囊工程有限公司，山东 济南 250101）

针对船舶上排下水橡胶气囊的爆炸问题，建立分析计算模型，将爆炸能量分为储存的内能和囊体变形产生的变形能。采用TNT当量模型，利用“虚拟距离”计算冲击波超压强度，并从爆炸冲击波影响的超压特点和囊体多种爆炸破坏方式2方面定量评估爆炸的危害性。通过改进气囊的结构形式来避免不利爆炸破坏形式的产生，界定爆炸的安全空间，为船用气囊的设计计算及工程施工安全评估提供分析方法。

船用气囊；爆炸；压缩气体；虚拟距离；TNT当量模型

0 引 言

船舶上排下水橡胶气囊（简称船用气囊）广泛应用于船舶上排下水、沉箱起重移运、其他重物搬运及水下安装工程的助浮等领域中，其因受场地限制少、无需大型的机械设备而具有缩短工程周期、节省大量资金的优势。20多年的发展实践证明，船用气囊具有安全高效、绿色环保和机动灵活等特点。由于船用气囊在使用过程中内部会充满压缩气体，属于具有一定弹性的压力容器，必然会受橡胶材料老化、超压及强度降低等因素影响而发生物理爆炸事故，造成严重的财产损失和人员伤亡。船用气囊的爆炸与传统的压力容器相似，由于囊体的材质橡胶具有柔性和弹性，其爆炸碎片释放的能量和残余变形能量占总爆破能量的比重很小，爆炸能量主要以冲击波的方式向外释放，产生大量空气冲击波。该冲击波可将建筑物摧毁，使设备及管道遭到严重的破坏。因此，合理地分析计算船用气囊发生物理爆炸时所产生的冲击波的强度具有十分重要的实践意义。

目前，对金属材质的压缩气体容器的物理爆炸冲击波超压强度的计算方法主要有TNT当量模型、AICHE模型和计算流体力学（Computational Fluid Dynamic，CFD）等3种。由于这些方法的适用条件不同，本文从各种计算理论在实际现场应用的特点出发，采用TNT当量模型对船用气囊的爆炸冲击波超压强度进行分析。

1 爆炸模型

1.1 储存的能量

船用气囊爆炸时不存在化学变化（如燃烧、化学反应等），爆炸产生的最大能量应与其储存的最大能量相等，储存的能量主要包括内能和变形能2部分。

1.1.1 内能

储存的能量来自于增大空气压缩机（以下简称空压机）的压力所做的功，空压机将空气压入到船用气囊内部，船用气囊内的空气量不断增多并被压缩，气压逐渐增大，使得船用气囊的内能随之增大。

1.1.2 变形能

船用气囊的材质为橡胶，并用尼龙线做骨架。这2种材料都具有大弹性特征，尤其是骨架材料具有很大的弹性变形量，其扯断伸长率达21%。船用气囊在持续充入空气至理论上的稳定状态后，继续充入空气会使骨架材料受到内压的作用，囊体继续膨胀，囊体壁发生较大的弹性变形，储存为变形能。

船用气囊的爆破与钢制压力容器的爆破是不同的，主要表现在以下2方面：

1) 钢制压力容器爆破时的变形量微小，其变形能可忽略，容积基本为固定值；

2) 橡胶气囊的变形量和体积随着压力的增加而增大，储存的能量也很大，又因在爆破时其体积无法测量，只能通过经验公式模拟得到，这是在总的爆炸能量中对弹性能进行单独处理的主要原因。

1.2 模型的能量计算

在TNT当量模型计算法中，压力容器的内部压力和体积是固定不变的，是能计量的标准状态，而船用气囊的体积，随着内部压力的增加而增大，直至爆炸瞬间，这是船用气囊采用TNT当量模型计算法不同的前提条件。基于这种特性，可将总的爆炸能量E0分为包含理论参数、固定体积条件下的TNT当量模型计算的能量E1和因弹性膨胀变形而增加的能量E2，即

1.2.1 压缩气体能量

热力学有效方法认为，压缩气体的物理爆炸能等于物质进入环境时所需的等效最大机械能，采用公式法计算物理爆炸能，可得

式(2)中：1P为船用气囊爆炸时的压力；0P为环境压力；V1为压缩气体的体积。

1.2.2 弹性变形能量

船用气囊因弹性变形而储存的能量E2是空压机充气做功产生膨胀变形所转换的能量。设船用气囊的内力为F，活塞移动距离为Δs，则空压机所做的功为

式(3)中：A为活塞面积；ΔV为单位体积。从开始充气至船用气囊爆破，空压机所做的功为

本文压力与体积的关系为P=P( V)，实际可表示为

式(5)中：a和b可采用实际测量统计分析数据的方法来确定。

表1为直径1.5m，长度5m的船用气囊在不同压力下的外形尺寸、推算的理论体积及体积的变化情况，根据体积累计变化数据ΔV进行线性回归分析（见图1），得出压力的趋势线关系式为

表1 实测数据

实际上，经常以压力P作为参数进行线性回归分析（见图2），则得出体积的趋势线关系式为

图1 ΔV-P关系图

图2 P-ΔV关系图

由此可得空压机所做的功为

1.2.3 总能量

船用气囊的总能量为

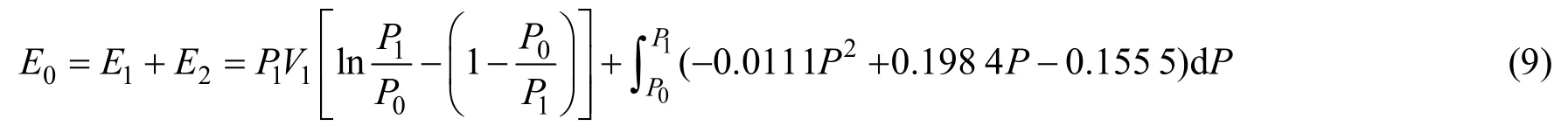
此时船用气囊的总体积为

1.3 当量模型参数的计算

由于船用气囊具有一定的体积，其爆炸不是点源爆炸，直接将气体的物理爆炸能类比为TNT爆炸能不合适，基于Prugh提出的“虚拟距离”TNT当量模型定义船用气囊表面最大超压与TNT爆炸超压相等时的超压距离和船用气囊半径的差值并进行修正，利用TNT爆炸曲线预测超压，计算步骤[1]如下。

1) 计算TNT当量质量WE为

式(11)中：ETNT为TNT的爆炸热，取4.7×106J/kg；WE为爆破能量E0的TNT当量质量。2) 计算容器表面冲击波压力Pj为

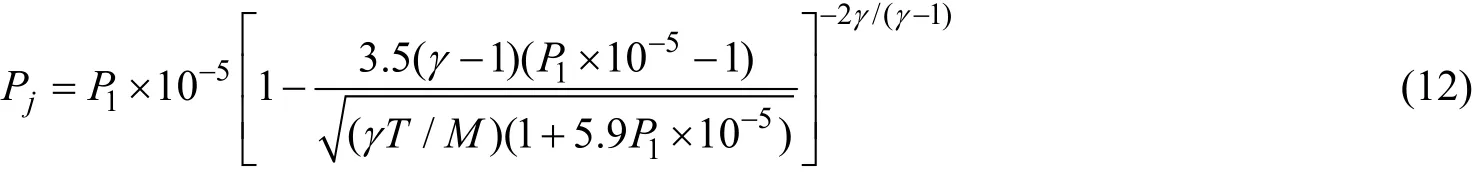
式(11)中：γ为气体绝热指数，空气为γ=1.4；T为膨胀气体的初始温度；M为膨胀气体的相对分子量。

3) 计算比拟距离ZS为

式(13)中：a，b，ci为常数；a=-0.21436；b=1.350；ci的取值见表2。

表2 ci的取值

4) 计算虚拟距离Rx为

式(14)中：n为船用气囊的当量半径。

5) 计算目标与容器中心距离对应的比拟距离ZR为

式(15)中：R为目标点与船用气囊爆破中心的距离。

6) 计算目标与船用气囊爆炸中心对应的比拟距离下的冲击波超压PZR为

例如，对于直径为2m，圆筒身部长度为6m的船用气囊，爆炸时内部的压力为1.75MPa，其TNT爆炸当量质量为25.8kg，计算得到的超压值对应的超压半径见表3[2]。

表3 超压计算结果

2 爆炸波及半径的快速估算

船用气囊爆炸造成人员伤亡和财产损失主要是冲击波所致，根据超压冲量的准则对爆炸波及半径（包括死亡半径和重伤半径）进行快速估算[3]。

2.1 死亡区

假设起点为爆炸中心，则以该点为中心，半径为Ra的区域为死亡区，Ra称为死亡半径。处于该区域内的人员无防护时因爆炸冲击波致死的概率为50%。

2.2 重伤区

假设起点内径为Ra，外径为Rb，则由内径和外径围成的环形区域为重伤区。该区域内的人员因冲击波而导致耳膜破裂的概率为50%，此时的冲击波超压为44kPa。

例如，对于直径为2m，圆筒身部长度为6m的船舶上排下水气囊，爆炸时其内部的压力为1.75MPa，死亡半径为3.5m，重伤半径为4.9m，对比表3中的超压数据结果，快速估算的结果具有一定的参考价值。

3 爆炸破坏的形式

船用气囊本体爆炸与金属罐类物理爆炸不同，后者在形成冲击波的同时，罐体被炸裂并有部分碎片等[4]。经过多次试验，前者的爆炸破坏形式主要有以下4种。

3.1 开裂

这种爆炸形式的破坏性较小，囊体没有因断裂而飞溅出去，对外界影响较小。从安全性和可靠性考虑，符合设计的破坏形式常表现为“一”字爆裂和“十”字爆裂2种（见图3）。

3.1.1 “一”字爆裂

爆炸时沿船用气囊的周向在身部爆裂开来，局部开裂或贯穿整个圆筒身部。这种爆炸形式的主要原理是骨架材料的周向强度低于轴向强度，是一种比较安全的爆炸形式。但是，由于2个方向上的强度不一样，在设计生产时骨架材料的轴向强度过剩，有浪费材料、利用率降低的缺点，对节约材料成本不利。

3.1.2 “十”字爆裂

爆炸时沿船用气囊的周向和轴向同时爆裂，爆裂开口形成十字状或丁字状。由于这种爆裂开口能形成大的压力释放空间，其爆裂长度有限，不会导致气囊沿周向破坏断裂成2节。从骨架材料的强度分析，周向和轴向的强度相当，强度均匀性较好，能最大限度地发挥骨架材料的强度性能，表明对材料的利用效率和性价比较高。这种爆炸形式是设计制造追求的目标。

3.2 断裂

3.2.1 能量估算方法

这种爆炸形式与开裂相比，破坏性增强，囊体断裂后可能形成一定体积、一定质量的飞溅物及碎片等，属于不安全的爆炸破坏形式。爆炸后残余囊体断裂成2节，对此进行能量估算的方法有气压做功估算法和部分爆炸能转换法2种。

3.2.1.1 气压做功估算法

在爆破瞬间，考虑内部压力对囊体轴向截面的作用，采用气体做功的原理估算爆炸后断裂成2节的囊体的瞬间动能和速度。

在身部断裂，其气压作用的截面为囊体的圆形横截面，设气囊直径为D，在爆破的瞬间气压为P，作用的行程为ΔL，则压力所做的功为

若断裂后的某部分的质量为m，则根据气压做功转换为囊体的动能W=E，即

由此可计算出断裂部分的瞬间速度为

3.2.1.2 1%爆炸能转换方法

通过将部分爆炸能转换为动能进行爆炸残余囊体的能量估算，即假设有1%的爆炸能转换为残余体的动能能量，其原理是根据Brode方程来计算爆炸能，即

假设有1%的爆炸能转换为动能，在身部断裂成2节，其中一节质量约为m，则该部分断裂囊体获得的动能为

将数据代入到式(23)中，可得每节的初始速度为

根据实际爆破情况及上述估算公式可知：

1) 在圆筒状断裂部位越靠近两端，爆破质量较小的参与体获得的动能越大，飞溅出去的破坏力越大；

2) 从圆筒状中间位置断裂形成对称的爆破残余体，其对外的破坏力较弱。

利用上述2种方法估算断裂后囊体残余部分的速度和动能，以此为参考评估破坏风险。

3.2.2 身部断裂

爆炸导致囊体圆筒部位沿周向一圈发生裂口，从而使船用气囊囊体断裂为2节（见图4），爆炸的巨大能量会使2节残余体以较大的速度向两侧反向移动或飞出，从而形成对外撞击，破坏风险大，破坏程度严重。这种形式的爆炸主要是囊体骨架材料的轴向强度小于周向强度，沿轴向的骨架材料强度先失效所致，相对来说也是周向强度余量较大所致，存在性能成本匹配的问题。

图4 断裂方式示意

3.2.2.1 速度估算

若囊体直径D=1m，圆筒身部长度为3m，自重为3000kg，则容积V=2.88 m3。若爆炸时的压力设为P1=2 MPa ，按照1%爆炸能转换法估算，可得

若囊体在身部中间形成对称的2节，则每节的质量m≈150kg，爆炸瞬间每节囊体获得初始速度为

若采用气压做功估算法来计算，假设做功距离ΔL=150 mm，则爆炸残余囊体的瞬间速度为

由上述2种估算方法可知，其结果相差不大，表明2种估算方法具有一致性。

3.2.2.2 安全距离估算

从飞溅距离的角度分析，爆炸发生时，囊体在断裂成2节后，高速向外飞溅，因内部气体急速释放，内部压力减小，下部接触地面的部位因摩擦而受到减速作用，上部因压力外泄而出现向上的翻转弯矩，导致断裂后的残余体在滑行的同时有翻滚的趋势，向上倾斜着飞溅出去，直至静止。该过程中的作用时间非常短，假设作用时间为0.1s，则可估算滑行的减速度和滑行距离分别为

式(29)中：s=2.8m为估算值，实际上飞溅滑出的距离可能更大。

若爆破位置在圆筒和锥头的过渡区（如图4b）所示），此时较小端囊体的质量约为50kg，则按1%能量转换法估算的爆破瞬间的速度可达98.5m/s，按气压做功方法估算的爆破瞬间的速度为95.0m/s。由此可见，其飞溅出去的速度约为囊体居中断裂飞溅速度的2倍，滑出距离至少有5m，这也是在不考虑爆炸超压情况下对安全距离的最低要求。

3.2.2.3 能量估算

爆炸残余囊体瞬间速度达到56m/s，动能约为235kJ，相当于一个重100kg的人从240m高空坠落到地面所产生的动能。

若在爆破的囊体周围安装防护屏障挡板，则在不考虑空气冲击波对挡板的影响的情况下，以冲量的方式估算屏障挡板受到的冲击力为

3.3 气嘴钢制件脱离

气嘴钢制件脱离是最危险的一种爆炸形式，气嘴受强大的内部压力作用从囊体的橡胶层中压裂迸出，破坏后果可能表现为气嘴钢制件瞬间脱离后高速飞出击中物体及脱离后橡胶残余口的高速气流引发冲击破坏。

图5 气嘴钢制件脱离飞出示意

在嘴断脱离囊体部位，采用气压做功的估算方法估算气嘴的飞出速度和飞出距离，暂不考虑气流的冲击影响。

以上述参数为例，设爆炸时的压力P=2 MPa ，根据气嘴与橡胶的结合体的结构特征参数，常规气嘴的质量m=2.5 kg ，气嘴上气压作用圆直径D=200 mm，从橡胶体脱离的距离（即气压所做功的距离）ΔL=100mm，则气嘴脱离的瞬间速度为

气嘴为金属钢制件，爆炸瞬间具有的动能约为6300J，相当于步枪子弹发射能量的6倍以上，一旦击中人体，会当场击穿并致命。此外，经估算，其在空中飞出的距离最少为23m，若考虑落在地面后可能滑行一段距离，其飞出的距离会更大。上述计算假设气囊直径为1m，若按直径为2m估算，则其飞出的距离将达到32m以上。因此，气嘴轴向爆炸很危险，要有足够大的安全距离。

4 安全空间的定量界定

根据上述对船用气囊爆炸的冲击波分析和破裂形式分析，应通过同时改进产品的结构和界定安全空间来降低或避免爆炸造成的人员伤亡与财产损失。

4.1 结构改进

通过改变船用气囊的骨架结构形式，对危险部位进行局部加强，避免各种不利的爆破形式，减少爆破的影响空间，从而提高可靠性和安全性。采取的主要措施有：

1) 轴向强度大于周向强度，避免身部断裂发生飞溅；

2) 对锥部与圆筒部位过渡处进行加强，避免该部位发生断裂；

3) 对气嘴与橡胶体结合部位进行局部加强，避免气嘴脱离飞出。

4.2 界定安全空间

对爆炸产生的冲击波超压影响空间和囊体断裂造成的影响空间进行综合分析，根据超压半径及危险程度的不同绘制影响空间区域图（见图6），界定安全空间[5]。

图6 影响空间区域图

图6b)为图6a)的俯视图，在图6中：

1) A区域为死亡区域，在该区域内会导致人员死亡；

2) B区域为重伤区域，在该区域内会导致人员重伤；

3) C区域为轻伤区域，在该区域内会导致人员轻伤；

4) D1区域和D2区域为危险区域，在该区域内会因气嘴或囊体的残余体飞出而导致人员重伤或轻伤；

5) S区域为安全区域，在该区域内不会危及人身安全。

在对船用气囊进行充气测压检验、施工操作时，根据爆炸超压的理论计算结果绘制区域分布图，对界定安全工作空间、执行安全范围的警戒具有重要的现实指导意义。

5 结 语

本文通过为船用气囊的爆炸建立分析计算模型，提出从爆炸冲击波影响的超压特点和囊体多种不同爆炸破坏形式2方面来定量评估爆炸的危害性，并通过对船用气囊的结构改进，避免不利爆炸破坏形式产生；综合绘制和界定爆炸的安全空间，为船用气囊的设计计算提供分析方法，对提高气囊产品的安全可靠性和工程应用实践操作、安全评价具有很大的参考价值。

[1] 党文义，刘昌华. 压缩气体容器物理爆炸计算模型[J]. 大庆石油学院学报，2010, 34 (2): 104-107.

[2] 李铮. 空气冲击波作用下人的安全距离[J]. 爆破与冲击，1990, 10 (2): 135-144.

[3] 刘鹏，王志全，贺红霞. 二氧化碳储罐物理爆炸能量及波及半径的定量评价[J]. 天然气化工，2004, 29 (3): 76-77.

[4] 陈汝训. 纤维缠绕压力容器爆破压强计算[J]. 宇航材料工艺，2000, 30 (6): 28-31.

[5] 张卫强，焦强，崔锋. 压力容器爆炸伤害事故后果分析及评价[J]. 科技信息，2009 (15): 493.

Study on Marine Airbag Explosion Model and Damage Based on Energy Method

ZHAO Dian-hua，DUAN Qing-ling

(Shandong Nanhai Airbag Engineering Co., Ltd., Jinan 250101, China)

A calculation model is established to solve the explosion problem of marine airbag during ship landing and launching. It divides the explosion energy into two sorts - the energy stored internally and the deformation energy due to the deformation of air sac. Based on the TNT equivalent model, the overpressure of shockwave is calculated according to“virtual distance” to evaluate the harmfulness of the explosion from two aspects, i.e., the overpressure characteristics of the shock wave and the explosion damage type of the sac. Thus adverse explosion damages can be avoided by improving the sac structure, and the safe space of explosion could be defined. This study provides an analysis method for the design calculation and an evaluation for safe construction of marine airbags.

marine airbag; explosion; compressed gas; virtual distance; TNT model

U671.5

A

2095-4069 (2017) 05-0015-08

10.14056/j.cnki.naoe.2017.05.003

2017-01-19

山东省技术创新项目（201630101046）

赵殿华，男，高级工程师，1977年生。2001年毕业于山东农业大学机电一体化专业，现从事气囊及打捞产品技术研究工作。