敏感器故障诊断与容错控制一体化设计*

刘细军，刘成瑞，刘文静

(北京控制工程研究所,北京 100190)

*国家自然科学基金资助项目(61203093、61573060、61640304).

敏感器故障诊断与容错控制一体化设计*

刘细军，刘成瑞，刘文静

(北京控制工程研究所,北京 100190)

针对卫星敏感器故障情况下的故障诊断与容错控制一体化设计问题，本文将敏感器有效性因子和控制器增益作为整体，利用区域极点配置方法设计综合输出反馈控制律，保证了良好的系统性能；再利用敏感器偏差的最优估计方法进行实时估计敏感器有效性因子，反解即可得到控制器增益，保证了控制的实时性和快速性；最后通过仿真验证了所提方法的有效性.

故障诊断；容错控制；航天器；有效性因子；区域极点配置

0 引 言

卫星正朝着复杂化和大规模化发展，对卫星控制系统的可靠性和自主运行能力的要求也大幅度提高.卫星的姿态确定是卫星稳定运行的基础，而恶劣的太空环境使得姿态敏感器故障难以避免，目前的应对策略主要是敏感器备份，而这会大大加重系统的负担.另一方面，一些故障诊断方法需要积累一定时间的数据才能诊断出故障，这段时间内卫星仍按照原有控制律运行，这会浪费有限的燃料，严重的会导致卫星姿态发散，甚至卫星解体.如何摆脱对硬件冗余的依赖，充分利用星上的有限资源实现快速有效的故障诊断与容错控制一体化是亟需解决的问题.

目前关于敏感器故障的诊断方法已有一定成果.文献[1]提出一种利用奉献观测器诊断敏感器故障的方法，该方法能克服能观性条件的限制，但该方法建立在已知控制系统只有敏感器发生故障的前提下.文献[2]针对单敏感器故障提出了一种基于卡尔曼滤波器的对新息均值和方差变化敏感的故障诊断方法并应用于无人机平台.文献[3]利用高频率输出的星敏感器姿态信息和卫星动力学方程获得高精度估计信息，用角速度估计值与不完整配置的陀螺进行比对达到故障诊断的目的.文献[4]利用星敏感器与陀螺输出值之间的解析冗余关系，通过设计两个滤波器实现对不同星敏感器的故障隔离，采用最小方差估计器得到包含目标星敏感器故障信息的残差，通过检验残差评价值是否超过阈值实现对目标星敏感器故障的检测.文献[5]用二级卡尔曼滤波器诊断出故障敏感器并隔离，并根据控制重构策略重新设置反馈控制器参数；但是这些方法旨在检测出故障部件以便切除，而要真正摆脱硬件冗余还需要研究如何充分利用未完全失效的部件完成控制任务.目前针对故障诊断与容错控制一体化的文献较少，且集中于面对执行器故障.文献[6]用测量有效性因子描述敏感器故障，然后用二级卡尔曼滤波算法进行估计出测量有效性因子并用于后续的容错控制.文献[7]针对敏感器故障设计了动态输出反馈控制器，用动态部分补偿故障诊断结果；文献[8]针对无陀螺卫星姿态自主确定系统提出了基于残差加权平均和的故障诊断算法与相应的系统重构方法.

本文以卫星姿态控制系统为研究对象，考虑敏感器故障情况下的故障诊断与容错控制一体化设计方法.首先将有效性因子和控制器增益作为整体，通过区域极点配置的方法将闭环系统极点配置在合理的区域内来设计综合控制律，然后通过基于测量偏差的最优估计方法进行有效性因子估计，根据估计结果与综合控制律结合进行反解得到控制器增益.由于闭环系统极点始终落在扇形稳定区域内，可以保证系统有良好的性能，同时通过有效性因子的实时估计来实时调整控制律，这又保证了控制的实时性和快速性.最后通过仿真验证了所提方法的有效性.

1 故障诊断与容错控制一体化设计

对于线性定常系统

(1)

式中，x∈Rn×1为状态变量，u∈Rp×1为控制量，y∈Rm×1为测量输出，w和v为线性互不相关的高斯白噪声，分别为系统噪声和敏感器测量噪声.

由于长时间工作及部件老化的影响，敏感元件易失效而产生输出异常波动以及输出端的未知偏差，即发生敏感器故障.敏感器故障的表示方法有加性故障和乘性故障两种，采用乘性故障的表示方法为

(2)

γi取值与故障的对应情况如下：

4)γi=1时正常输出.

当敏感器出现故障时，将式(2)代入式(1)中可得包含故障的线性系统模型

(3)

式中，w、v为彼此不相关的零均值白噪声，对应的方差阵分别为W、V.

考虑到实际的控制系统多采用计算机控制，对上述系统模型进行离散化，采样周期为T.离散后的模型为

(4)

对于系统(3)要设计输出反馈控制器

u=K(y+Δy)，K∈κ

(5)

使得闭环系统

(6)

的极点位于图1所示的扇形区域S(α,θ,r)内，可以保证系统衰减度不小于α，阻尼比不小于ζ=cosθ，自然频率不大于ωn=rsinθ，进而保证最大超调、上升时间、调节时间等过渡过程指标.式(5)中κ为给定的有界矩阵集，由执行器的物理特性决定.

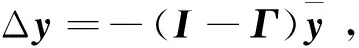
引理1：闭环系统(6)的所有特征值均在区域S(α,θ,r)中的充要条件是存在一个正定对称阵X使

(7)

由式(7)可知，KΓ可以作为一个整体进行求解，定义为K*=KΓ.通过求解式(7)可以得到综合控制律K*，再通过一定的估计方法估计出Γ就可以通过K=K*Γ-1反解得到控制器增益K.这样做

的好处是可以离线设计综合控制律，卫星在轨只需实时估计有效性因子，然后调整控制律，可以大大减少计算量，并且保证良好的系统性能.

2 基于BMI的综合控制律求解

由于式(7)不是标准的线性矩阵不等式，无法利用线性矩阵不等式工具箱进行求解，需要通过以下迭代步骤[10]进行求解上述双线性矩阵不等式.

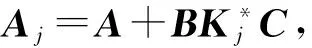
mint:t,X1,X2,X3满足

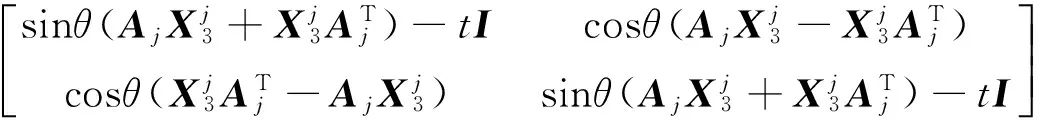
(8)

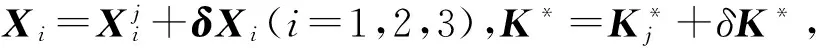
mint:δX1,δX2,δX3,δK*满足

(9)

3 敏感器有效性因子估计

为便于估计，需将含有效性因子的乘项转化为已知项.需要对输出方程作以下处理.由系统(4)的输出方程易得

(10)

从而式(3)可化为

(11)

再作如下变换：

=Cx+Eγ+Γ-1v

由于正常情况下噪声的系数矩阵为单位阵，且一定的噪声增大不影响增益型故障估计，可假设噪声系数矩阵为单位阵.则系统(4)变为

(13)

基于测量偏差的最优估计方法[11]，将有效性因子γ作为测量偏差进行估计，估计结果与前述控制律结合组成所需的容错控制.有效性因子的迭代过程如下：

状态量的无偏估计

(14)

偏差估计

(15)

最优状态估计

(16)

通过以上迭代过程可以得到乘性故障的敏感器有效性因子，进而可以反解得到所需的容错控制律.

4 仿真验证

考虑卫星刚体模型，其姿态动力学方程可表示为

(17)

其中，H=Ibω为卫星转动角动量，Ib=diag{Ix,Iy,Iz}为卫星转动惯量矩阵.Td为干扰力矩，u为星体所受控制力矩，记为u=[uxuyuz]T.展开为

(18)

轨道坐标系在空间中的转速为(0,-ω0,0).基于小角度假设，卫星姿态运动学方程为

(19)

其中，φ,θ,ψ分别为星体的滚动角、俯仰角和偏航角.

将(19)代入(18)中得以欧拉角描述的卫星姿态动力学方程

(20)

取状态变量为

根据式(20)建立线性系统状态方程

(21)

选取星敏感器和陀螺作为敏感器，考虑八面体构型陀螺系统[12]，其相应的输出方程为

y=Cx+v

(22)

其中，

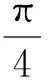
通过上述算法，仿真得到

对应的闭环极点为λ1,2=-1.507 6±0.347 4i，λ3,4=-1.507 6±0.323 8i，λ5,6=-1.509 7±0.010 7i.

针对以上的卫星控制系统，设置了两种故障模式，增益型故障和输出卡死故障，分别进行仿真.

故障模式一：增益型故障，有效性因子矩阵为Γ=diag{1,1,1,1,0.8,1,1,1,1}.若不采取容错控制策略，卫星的姿态角及角速度变化如图2所示.采取上述的故障诊断与容错控制策略后，姿态变化如图3所示.

故障模式二：输出饱和故障，有效性因子矩阵为Γ=diag{1,1,1,1,0.01,1,1,1,1}.若不采取容错控制策略，卫星的姿态角变化如图4所示.采取上述的故障诊断与容错控制策略后，姿态输出如图5所示.

仿真结果分析：当卫星敏感器出现增益型故障时，如不采取容错控制策略，卫星姿态将出现较小偏差；当卫星敏感器出现输出卡死故障时，卫星姿态将出现较大偏差.当然，在实际中出现输出卡死故障时，应当及时切除故障敏感器，避免故障的闭环传播，本文针对的主要是未完全失效的敏感器.仿真结果表明，采用上述故障诊断与容错控制一体化设计策略，可以有效估计偏差，消除姿态偏差，从而验证了上述算法的有效性.

5 结 论

本文基于区域极点配置和敏感器偏差的最优估计方法设计了卫星姿态控制系统的故障诊断与容错控制一体化设计.利用摄动线性化的方法能有效求解双线性矩阵不等式，保证了闭环系统的良好的系统性能.该容错控制算法将故障诊断过程和控制器的设计过程结合起来，保证了控制的实时性和快速性.同时，闭环系统的控制律的设计可以提前设计，只需实时估计有效性因子，大大减少了星上计算机的计算量.仿真验证了该方法的可行性和有效性.

[1] 江耿丰，邢琰，王南华.利用奉献观测器诊断红外地球敏感器故障的新方法[J].航天控制，2007，25(3)：38-42.

JIANG G F,XING Y,WANG N H. A new fault diagnosis approach for infrared earth sensor based on dedicated observers[J].Aerospace Control, 2007, 25(3): 38-42.

[2] CHINGIZ H. An innovation approach based sensor fault detection and isolation[J]. IFAC-PaperOnLine, 2016,49(17):420-425.

[3] 张云，王培垣.基于星敏感器角速度估计的陀螺故障诊断[J].航天控制，2004,22(3)：93-96.

ZHANG Y, WANG P Y. Fault diagnosisof gyroscope based on estimated angular rate using star sensor[J].Aerospace Control, 2004, 22(3):93-96.

[4] 袁泉，何英姿，邢琰，等.基于线性最小均方差估计的星敏感器故障诊断[J].空间控制技术与应用，2013，39(2)：30-35.

YUAN Q, HE Y Z, XING Y, et al. Fault diagnosis for star sensors based on linear minimum mean square filter[J].Aerospace Control and Application, 2013, 39(2):30-35.

[5] FIKRET C, CHINGIZ H. Reconfigurable control of an UAV against sensor/actuator failures[J]. IFAC-PaperOnLine, 2015, 48(9):7-12.

[6] 陈雪芹. 集成故障诊断与容错控制研究及其在卫星姿态控制中的应用[D].哈尔滨：哈尔滨工业大学，2008.

CHEN X Q. The research of integrated fault detection and diagnosis and fault-tolerant control with its application in satellite attitude control[D]. Harbin: Harbin Institute of Technology, 2008.

[7] 胡芳芳. 卫星姿态H∞鲁棒容错控制与D-稳定性分析研究[D].哈尔滨:哈尔滨工业大学，2014.

HU F F. Research on H∞robust fault-tolerant control and d-stability analysis[D]. Harbin: Harbin Institute of Technology, 2014.

[8] 李钧.地球同步轨道卫星容错定姿定轨研究[D].西北工业大学硕士学位论文，2005.

LI J. Research on fault-tolerant attitude and orbit determination for geosynchronous satellite[D]. Master Dissertation of Northwestern Polytechnical University, 2005.

[9] 贾英民.鲁棒H∞控制[M].北京：科学出版社，2007: 165-166.

JIA Y M. RobustH∞Control[M]. Beijing: Science Press, 2007: 165-166.

[10] 王远钢.基于BMI方法的扇形极点配置输出反馈[J].自动化学报，2008，34(9):1192-1195.

WANG Y G. BMI-Based output feedback control design with sector pole assignment[J]. Acta Automatica Sinica, 2008, 34(9):1192-1195.

[11] WIILLIAM S. AGEE, ROBERT H. Turner. Optimal estimation of measurement bias[J]. National Technical Information Service, 1972.

[12] ARTHUR L. SATIN, et al., Evaluation of parity equations for gyro failure detection and isolation[J]. Journal of Guidance Control and Dynamics, 2015,1(1):14-20.

IntegratedDesignofSensorFaultDiagnosisandFaultTolerant

LIU Xijun, LIU Chengrui, LIU Wenjing

(BeijingInstituteofControlEngineering,Beijing100190，China)

A method for integrated design of fault diagnosis and fault tolerant is proposed for a class of sensor fault. First, the sensor effectiveness factor and the controller gain are taken as a whole, so we can construct a combined output feedback controller via the theory of regional pole assignment. Then an optimal estimation method is given to estimate the sensor effectiveness factor in real time, which can be used to solve the controller gain. The well designed combined controller can ensure the system achieving a good performance while the real-time estimated sensor effectiveness factor can ensure the control is real-time and rapid. Finally, numerical simulations demonstrate the effectiveness of the proposed approach.

fault diagnosis; fault tolerant; spacecraft; effectiveness factor; regional pole assignment

2017-01-12

V448.2

A

1674-1579(2017)05-0031-06

10.3969/j.issn.1674-1579.2017.05.005

刘细军(1992—)，男，硕士研究生，研究方向为故障诊断与系统重构技术；刘成瑞(1978—)，男，高级工程师，研究方向为航天器故障诊断与可靠性研究；刘文静(1980—)，女，高级工程师，研究方向为卫星控制系统故障诊断.