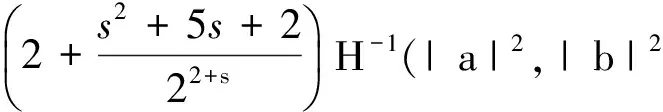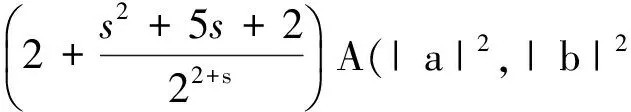关于Riemann-Liouville分数积分的Hermite-Hadamard型不等式
2017-11-08邱克娥彭长文
邱克娥, 彭长文
(贵州师范学院 数学与计算机科学学院, 贵州 贵阳 550018)
关于Riemann-Liouville分数积分的Hermite-Hadamard型不等式
邱克娥, 彭长文
(贵州师范学院 数学与计算机科学学院, 贵州 贵阳 550018)
主要建立2个关于已知函数导数的重要Hermite-Hadamard型Riemann-Liouville分数积分恒等式,进而得到关于某些特殊凸函数有意义的Riemann-Liouville分数积分的Hermite-Hadamard型不等式,如s-凸函数、m-凸函数、(s,m)-凸函数等.这些结果改进了一些文献中的有关结果,并结合几个常用的平均值给出应用.
Riemann-Liouville分数积分; Hermite-Hadamard型不等式;s-凸函数;m-凸函数; (s,m)-凸函数
1893年,Hermite和Hadamard给出了著名的Hadamard不等式(也叫Hermite-Hadamard不等式):若f(x)是闭区间[a,b]上的连续凸函数,则有
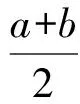
等号当且仅当f(x)为线性函数时成立.近些年来,Hermite-Hadamard不等式受到广泛关注并应用于生产实际及计算机领域,参见文献[1-3].更有许多学者对Hermite-Hadamard不等式做了大量的改进和推广,M.Z.Sarikava等在文献[4]的定理2中得到:设0≤a 其中 显然Hermite-Hadamard不等式是Riemann-Liouville分数积分的一种特殊形式,只需要α=1.对于分数积分的有关结果,参看文献[5-7].ZhuC.等在文献[8]定理2.3中得到如下结果: 定理1[8]设a 受上述不等式的启发,本文主要建立关于s-凸函数、m-凸函数、(s,m)-凸函数的左Riemann-Liouville分数积分的Hermite-Hadamard不等式,其中某些结果改进了上述不等式的结果. 为了方便,首先给出一些记号、凸函数的有关概念以及本文所需要的2个重要引理.记I是实数集R的一个子集,即I⊂R. 定义1[9]设函数f(x)在区间I⊂R+上有定义,若对任意x,y∈I和λ∈[0,1],都有 f(λx+(1-λ)y)≤λsf(x)+(1-λ)sf(y), 其中s∈(0,1],则称f(x)是I上的s-凸函数. 定义2[10]设函数f(x)在区间I⊂R+上有定义,若对任意x,y∈I和λ∈[0,1],都有 f(λx+m(1-λ)y)≤λf(x)+m(1-λ)f(y), 其中m∈[0,1],则称f(x)是I上的m-凸函数. 定义3[10]设函数f(x)在区间I⊂R+上有定义,若对任意x,y∈I和λ∈[0,1],都有 f(λx+m(1-λ)y)≤λsf(x)+m(1-λs)f(y), 其中(s,m)∈[0,1]×[0,1],则称f(x)是I上的(s,m)-凸函数. 不少学者关于s-凸函数、m-凸函数、(s,m)-凸函数得到许多Hermite-Hadamard不等式,可以参看文献[10-12].关于其他类型凸函数如MT-凸函数、Schur-凸函数、GA-凸函数的相关不等式,参看文献[13-15]. 引理1设a 证明 I1+I2-I3-I4-I5+I6. (1) 分别积分得 (2) (3) 且 (4) 且 (5) (6) 且 (7) 所以将(2)~(7)式代入(1)式可得 (8) 注1在引理1中,令α=1,则有 引理2设a 证明利用引理1,并注意到区间[a,mb]⊂[a,b],则该引理易得.证毕 2.1主要结果通过引理1和引理2得到如下结果,其中定理2中的分数积分不等式是定理1中不等式的加细. 定理2设a 其中,0<α≤1,B是贝塔函数; 其中α>1. 定理4设a 当α≥1时,下列分数积分不等式成立 2.2定理2的证明对任意t∈[0,1],由引理1及基本不等式(1+t)α<2α有 由于|f′(x)|是定义在[a,b]上的s-凸函数,则对任意t∈[0,1],对某些固定的s∈(0,1]有 且 因此 通过简单计算得到 由于对任意t∈[0,1],s∈(0,1],有不等式(1+t)s≤1+ts,所以 另一方面,对任意t∈[0,1],当α∈(0,1],有不等式(1+t)α≥2α-1(1+tα),所以 当α∈(1,∞)有不等式(1+t)α≥1+tα,所以 综上所述,当α∈(0,1]时 当α∈(1,∞)时 因此 其中 K′= 定理2得证. 注2在定理2中取α=s=1,则 得到文献[11]中的结果.该结果改进了文献[8]中的结果. 且 与定理2证明类似可得,定理3结论成立.证毕. 2.4定理4的证明由于|f′(x)|是定义在[a,b]上的可测(s,m)-凸函数,对任意t∈[0,1],对某(s,m)∈(0,1]2, 且 与定理2证明类似可得,定理4结论成立.证毕. 对任意实数α,β,α≠β,考虑文献[12]中的以下平均值: 命题1设a,b∈R,a 证明设f(x)=xn,α=1,应用定理2即可证.证毕. 命题2设a,b∈R,a 证明设f(x)=1/x,α=1,应用定理2即可证.证毕. 命题3设a,b∈R{0},a 同时 证明在命题1及命题2中,做替换a→b-1,b→a-1即可证.证毕. 致谢2015年省级本科教学工程建设项目(黔教高发[2015]337号)和基于ACM/ICPC问题驱动的《数据结构》课程教学改革项目(黔教高发[2015]337号)对本文给予了资助,谨致谢意. [3] CAL J, CARCAMOB J, ESCAURIAZA L. A general multidimensional Hermite-Hadamard type inequality[J]. J Math Anal Appl,2009,356(2):659-663. [4] SARIKAYA M Z, SET E, YALDIZ H, et al. Hermite-Hadamard’s inequalities for fractional integrals and related fractional inequalities[J]. Math Comput Model,2013,57(9/10):2403-2407. [5] DAHMANI Z. New inequalities in fractional integrals[J]. Nonlinear Sci,2010,9(4):493-497. [6] DAHMANI Z. On Minkowski and Hermite-Hadamard integral inequalities via fractional integration[J]. Ann Funct Anal,2010,1(1):51-58. [7] Dahmani Z. On some new fractional integral inequalities[J]. Inter J Math Anal,2010,4(4):185-191. [8] ZHU C, FECKAN M, WANG J. Fractional integral inequalities for differentiable convex mappings and applications to special means and a midpoint formula[J]. J Appl Math:Statistics and Informatics,2012,8(2):21-28. [9] HUDZIK H, MALIGRANDA L. Some remarks ons-convex functions[J]. Aequationes Mathematicae,1994,48(1):100-111. [10] TUNC M. On new inequalities form-convex functions via Riemmann-Liouville fractional integration[J]. Filomat,2013,27(4):559-565. [11] KIRMACI U S. Hermite-Hadamard type inequalities fors-convex functions[J]. Appl Math Comput,2007,19(3):26-35. [13] CHU Y M, KHAN M A, KHAN T U, et al. Generalizations of Hermite-Hadamard type inequalities for MT-convex functions[J]. Nonlinear Sci Appl,2016,9(6):4305-4316. [14] CHU Y M, WANG G D, ZHANG X H. Schur convexity and Hadamard’s inequality[J]. Math Ineq Appl,2010,13(4):725-731. [15] ZHANG X M, CHU Y M, ZHANG X H. The Hermite-Hadamard type inequality of GA-convex functions and its application[J]. J Ineq Appl,2010,11(1):1-11. On Hermite-Hadamard-type Inequalities for Riemann-Liouville Fractional Integrals QIU Ke’e, PENG Changwen (InstituteofMathematicsandComputerScience,GuizhouNormalUniversity,Guiyang550018,Guizhou) In this paper, we explore two important Hermite-Hadamard-type fractional integral identities including the first-order derivative of a given function. With the help of the fractional integral identities, some interesting and important Hermite-Hadamard’s inequalities involving Riemann-Liouville fractional integrals fors-convex,m-convex, (s,m)-convex functions are established, respectively. The results obtained in this paper provide a refinement of previously known results in the literature and some applications to special means of real numbers. Riemann-Liouville fractional integrals; Hermite-Hadamard type inequalities;s-convex functions;m-convex functions; (s,m)-convex functions 2016-02-15 贵州省科学技术基金(黔科合J字[2014]2142)、贵州省教育厅自然科学研究项目(黔教合KY字[2015]422号)和卓越工程师教育培养计划项目(黔教高发[2013]446号) 邱克娥(1986—),女,讲师,主要从事函数论的研究,E-mail:qke456@sina.com O122.3 A 1001-8395(2017)05-0644-07 10.3969/j.issn.1001-8395.2017.05.014 2010MSC:26A15; 26A51 (编辑 李德华)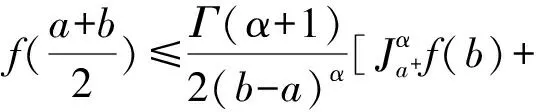

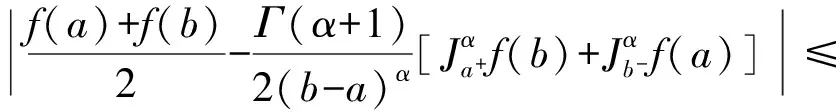

1 定义和引理

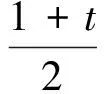

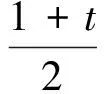













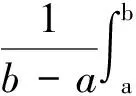
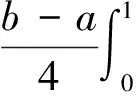
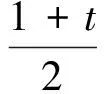
2 主要结果及证明
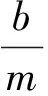

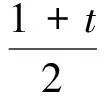
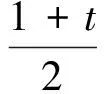
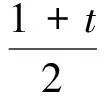
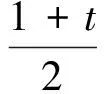





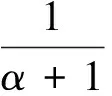









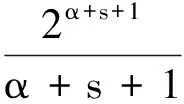


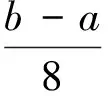

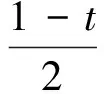
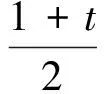
3 应用