一种新型开关耦合电感准Z源逆变器
2017-11-08宋奇吼刘文安
宋奇吼,刘文安,陈 莉,杨 飏
一种新型开关耦合电感准Z源逆变器
宋奇吼,刘文安,陈 莉,杨 飏
提出一种新型开关耦合电感准Z源逆变器,实现相同输入电压和直通占空比条件下逆变器输出电压的大幅提升。分析了新拓扑的工作机理、升压特性和控制策略,采用简单升压控制方法,通过Matlab仿真试验验证了新拓扑的可行性。
准Z源逆变器;开关耦合电感;升压能力
0 引言
传统电压源逆变器属于降压型逆变器,输出电压低,难以满足分布式发电系统的升压需求。为防止传统逆变器上下桥臂直通,传统电压源逆变器需要引入死区控制,不仅增加了输出电压的谐波含量,还增加了系统控制的复杂性[1,2]。
与传统逆变器相比,Z源逆变器具有可直通、控制简单、升压能力强的优点,能有效克服传统逆变器的不足,适应新能源发电的需求。文献[3]在Z源逆变器的基础上提出了准Z源逆变器。与Z源逆变器相比,准Z源逆变器具有输入电流连续、电容电压应力小的优点,但准Z源逆变器同样无法在不影响系统稳定性的前提下,通过控制直通占空比获得足够大的直流增益[4]。
1 准Z源逆变器技术发展现状
针对Z源/准Z源逆变器升压能力有限的问题,许多文献通过改进电路拓扑提升Z源逆变器直流升压能力,先后提出了开关电感Z源逆变器、扩展升压Z源逆变器、抽头电感Z源逆变器、耦合电感Z源逆变器等拓扑结构[5~20]。
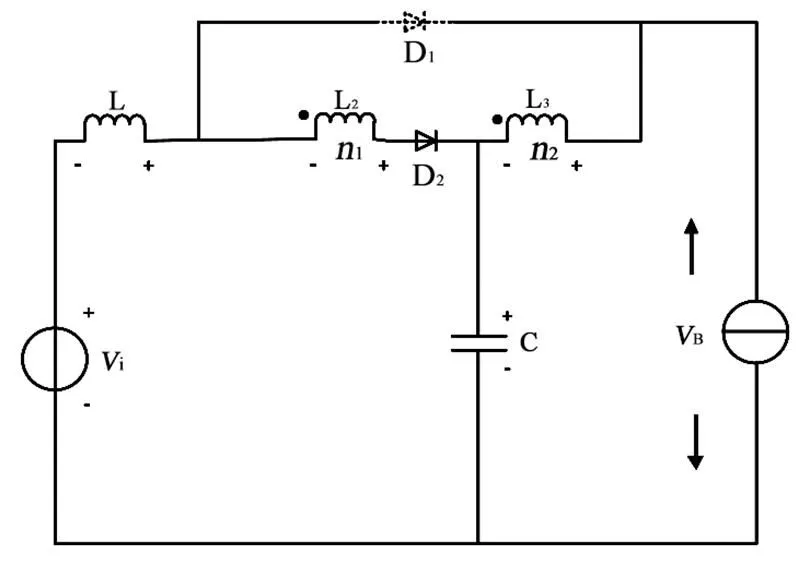
其中文献[11]以准Z源逆变器为基础,引入开关耦合电感升压思路,提出开关耦合电感准Z源逆变器(SCL-qZSI),其拓扑结构如图1所示。SCL-qZSI的升压比可表示为
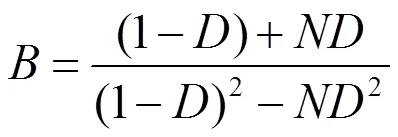
式中,为直流占空比;为耦合电感变比。
图1 开关耦合电感准Z源逆变器拓扑结构
与开关耦合电感相比,SCL-qZSI具有母线负极与输入电源负极共地、输入电流连续的优点,但也存在一些不足:SCL-qZSI升压能力有限,拓扑结构比较复杂,开关损耗较大。
为改进开关耦合电感准Z源逆变器拓扑结构,本文提出一种新型开关耦合电感准Z源逆变器(New Type Switched Coupled Inductor Quasi- Z- Source Inverter ,NTSCI-qZSI)。新拓扑结构简单可靠,具备更强的升压能力。
2 新型开关耦合电感准Z源逆变器
2.1 拓扑结构
以传统准Z源逆变器为基础,提出2种开关耦合电感准Z源逆变器:输入电流连续型开关耦合电感准Z源逆变器(图2 a)和输入电流断续型开关耦合电感准Z源逆变器(图2 b)。与传统准Z源逆变器相比,新型开关耦合电感准Z源逆变器以耦合电感替代Z源网络中的1个电感,在耦合电感之间插入1个二极管,同时以二极管代替Z源网络中的1个电容,利用工作模态变化提升直流链电压。
与图1所示拓扑结构进行比较,图2(a)所示输入电流连续型开关耦合电感准Z源逆变器具有输入电流连续、输入输出电压共地的优点,为此本文选取该电路拓扑为分析对象。
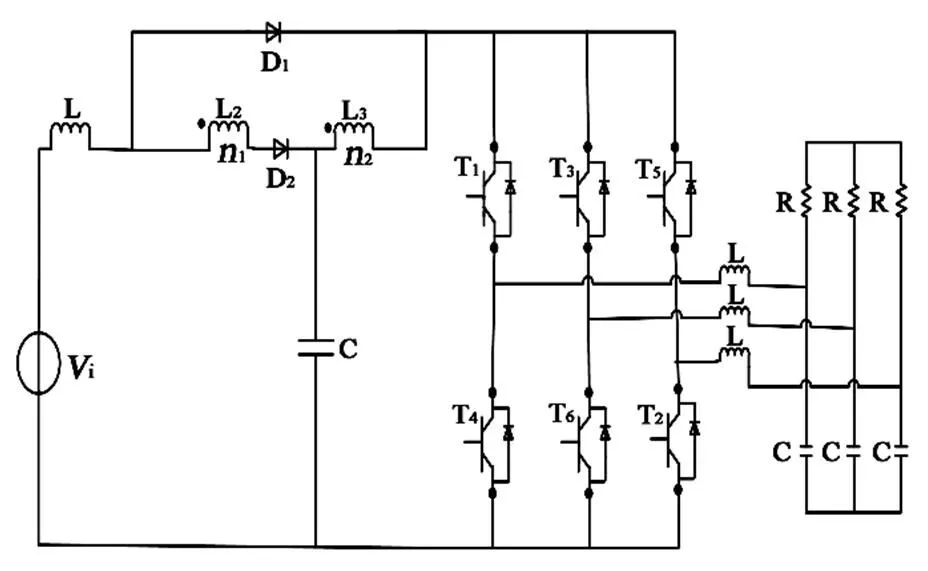
(a)输入电流连续型
(b)输入电流断续型
图2 新型开关耦合电感准Z源逆变器拓扑结构
为简化分析,将图中的耦合电感等效为理想状态,忽略漏感影响,耦合系数为1。原边匝数为1,副边匝数为2,定义耦合电感匝比为,耦合电感原、副边电压分别为Ln1、Ln2,则有1∶2,Ln1Ln2。
2.2 稳态情况下的工作原理
稳态情况下的开关周期包括1个直通零矢量状态、2个传统零矢量状态、6个有效矢量状态。为方便分析,可简化为直通零矢量状态、传统零矢量状态和有效矢量状态3种工作模态。
(1)模态I:直通零矢量状态。等效电路如图3(a)所示。该状态下,控制逆变桥上下桥臂直通,直流链电压为零。二极管D1承受正向电压导通,输入电源通过D1和逆变桥给电感L储能。电容C通过耦合电感副边和逆变桥线性放电,耦合电感副边储能。耦合电感副边承受电容电压,极性左正右负,耦合至原边后电压极性相同,因此二极管D2承受反向电压关断,此时系统满足:
(2)
(2)模态Ⅱ:传统零矢量状态。等效电路见图3(b)。该状态下,逆变桥开路,直流母线电流为零。耦合电感电压极性左负右正,二极管D1承受反向电压关断,D2承受正向电压导通,电容充电,电感L及耦合电感原边储能,此时系统满足:
(3)
(3)模态III:有效矢量状态。等效电路如图3(c)所示。该状态下,逆变桥等效为电流源,二极管D1关断,D2导通,输入电源、电感、耦合电感原边、耦合电感副边串联向负载供电,提升逆变桥直流链电压,此时系统满足:
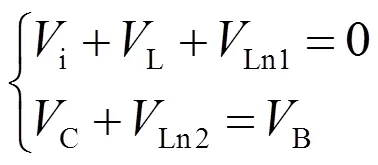
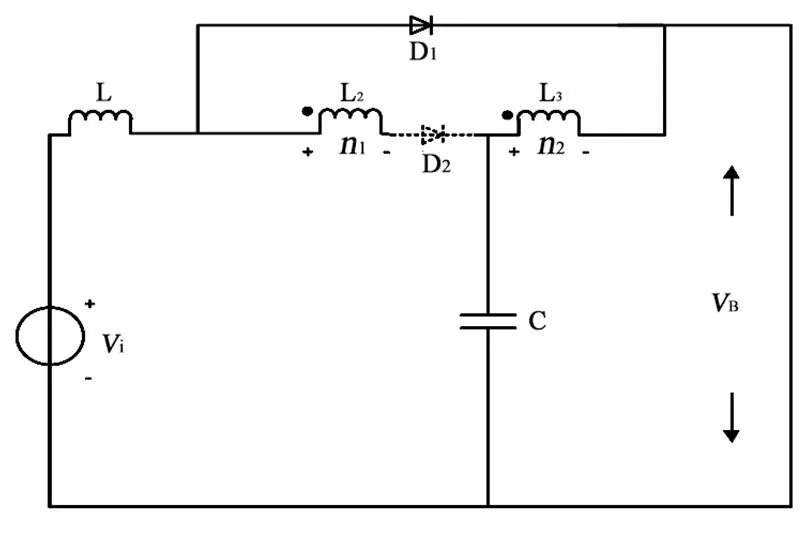
(a)直通零矢量状态
(b)传统零矢量状态
(c)有效矢量状态
2.3 升压特性分析
一个开关周期内,直通零矢量状态时间为0,传统零矢量状态时间为1,有效矢量状态时间为2。由式(2)、式(3)可见,传统零矢量状态和有效矢量状态下电感L与耦合电感承受电压相同。系统稳态时根据电感L及耦合伏秒平衡可得
-i+ (1-)[(1 +)C-i-B] = 0 (5)
-C+ (1-)(B-C) = 0 (6)
两式联立,可解得
(7)
结合式(3)可得直流链电压峰值B为
(8)
新拓扑的升压因子为
(9)
从式(9)可以看出,升压因子与耦合电感变比及直通占空比有关。图4为2时,准Z源逆变器(qZSI)、开关耦合电感准Z源逆变器(SCL-qZSI)及新型开关耦合电感准Z源逆变器(NTSCL-qZSI)的升压因子与直通占空比的关系曲线,可以看出,升压因子均随直通占空比的增大而增大,相同直通占空比条件下,新型开关耦合电感准Z源逆变器升压能力更强,且其直通占空比必须满足<1/(1)。图5为0.2时,开关耦合电感准Z源逆变器和新型开关耦合电感准Z源逆变器的升压因子与变比的关系曲线,从图中可以看出直通占空比确定后,随的增大而增大,且相同变比条件下新拓扑结构升压能力更强。
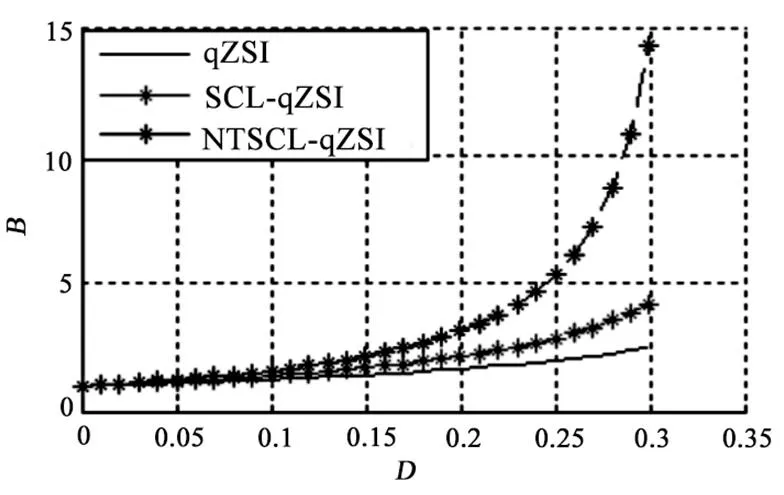
图4 升压因子B与直通占空比D的关系

图5 升压因子B与耦合电感变比N的关系
3 开关耦合电感准Z源逆变器控制策略
目前适于Z源逆变器的控制方式有:简单升压控制、三次谐波注入控制、最大升压控制等控制方式[12,13]。简单升压控制方式原理简单、易于实现;三次谐波注入控制通过在调制波中注入基波的三次分量实现直通占空比增大,提高升压范围;最大升压控制策略将逆变器的传统零矢量状态全部变为直通零矢量状态,可获得最大升压。为更好地体现新拓扑结构在提升直流链电压方面的能力,本文分析所采用的是简单升压控制策略,其原理如图6所示。
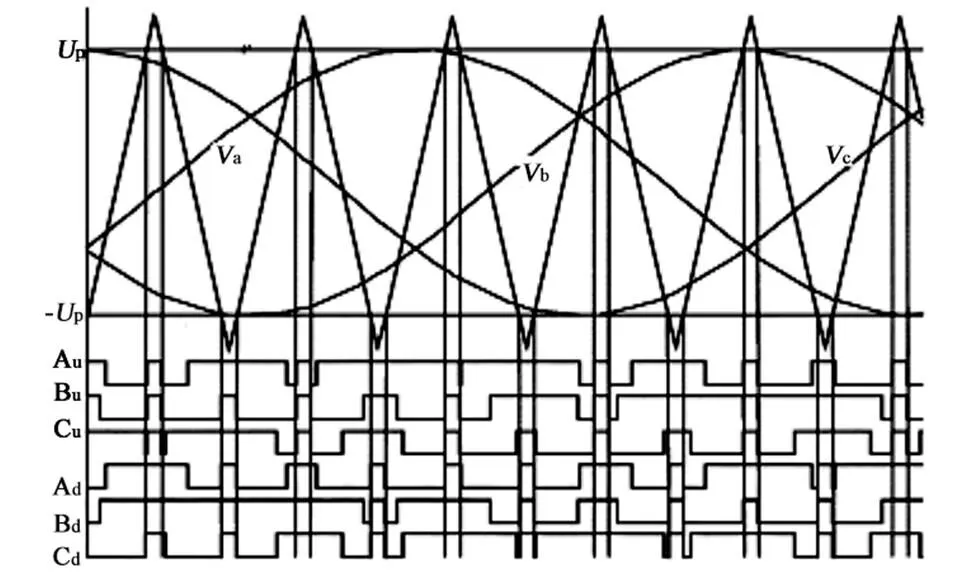
图6 简单升压调制原理
正弦调制度为,则输出电压基波幅值为
(10)
4 仿真验证
通过简单升压控制,利用Matlab/Simlink工具搭建新型开关耦合电感准Z源逆变器模型,电路参数如下:Z源电感1 mH,Z源电容=800mF,耦合电感变比2,耦合电感原边2200mH,耦合电感副边3200mH,输入电源电压i100 V,开关频率10 kH,直通占空比0.2,调制度0.8。实验结果如图7所示。
从仿真结果可以看出,开关耦合电感准Z源逆变器直流链电压为316 V,Z源网络电容电压为244 V,逆变器输出电压为120 V,与理论分析一致。
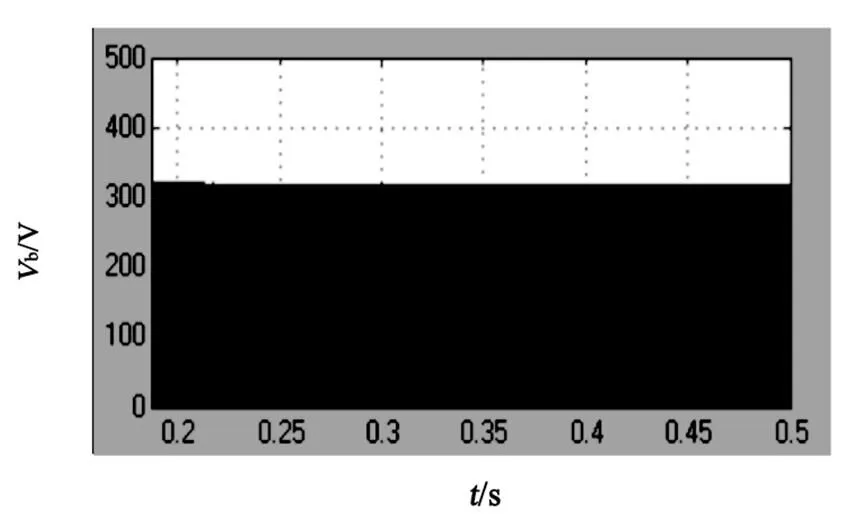
(a)直流链电压波形
(b)Z源网络电容电压

(c)逆变器输出电压波形
5 结语
本文基于准Z源逆变器,通过改变电路拓扑结构,提出新型开关耦合电感准Z源逆变器。新拓扑结构简单可靠,能大幅提升逆变器直流链电压,更好地满足分布式电源并网发电的需求。
[1] N. Mohan, T. M. Undeland, and W. P. Robbins, Power Electronics: Converters Application and Design. New York: Wiley, 2003.
[2] 吴茂刚,赵荣祥,汤新舟. 正弦和空间矢量PWM逆变器死区效应分析与补偿[J]. 中国电机工程学报,2006,26(12):101-105.
[3] Wei Qian, Fang Zhengpeng, Honnyong Cha. Trans- Z-source Inverters[C]. Proceedings of Power Electronics Conference, 2010, 1874-1881.
[4] N. Mohan, T. M. Undeland, and W. P. Robbins, Power Electronics: Converters, Application and Design. New York: Wiley, 2003.
[5] Miao Zhu, KunYu, Fang Lin Luo, IEEE transactions on power electronics: Switched Inductor Z-Source Inverter[J]. 2010,25(8),2150-2158.
[6] 石季英,刘文安,李春玲. 扩展升压Z源逆变器及其控制策略的研究[J],电气传动,2012,42(8):29-33.
[7] Chandana Jayampathi Gajanayake,Fang Lin Luo,Hoay Beng Gooi,Ping Lam So,Lip Kian Siow. Extended-Boost Z-Source Inverters[J].IEEE Transactions on Power- electronics, 2010, 25(10):2643-2645.
[8] LiD, Loh PC, ZhuM, et a1. Cascaded Switched Inductor and tapped-inductor Z-source inverters[C] IEEE Applied Power Electronics Conference.IEEE,2011:1661-1666.
[9] 周玉斐,黄文新,赵健伍,等. 抽头电感准Z源逆变器[J]. 中国电机工程学报,2012,32(27):126-134.
[10] Se-Jin Kim, Young-Cheol Lim, Switched Trans Z-source inverter using two isolated two-winding transformers[C], Proceedings of Power Electronics Conference,2014,677-681
[11] 周玉斐,黄文新,赵健伍,等. 开关耦合电感准Z源逆变器[J]. 电工技术学报,2014,29(6),31-39.
[12] Miaosen Shen , Jin Wang ,Alan Joseph , Fang Z. Peng. Maximum Constant Boost Control of the Z-Source Inverter[c]. IEEE IAS, 2004:143-144.
[13] 张超华,汤雨,谢少军. 改进Z源逆变器的三次谐波注入控制策略[J]. 电工技术学报,2009,24(11):116-117.
[14] 宋奇吼,刘文安,陈莉,等. 三电平Z源逆变器SPWM调制策略的研究[J]. 电测与仪表,2014,(14):83-87.
[15] 宋奇吼,陶红华,陈莉,等. 地铁牵引变电所综合电源监控系统研究[J]. 电测与仪表,2014,(11):107-113.
[16] 宋奇吼,刘文安,陈莉,等. 开关电感Z源三电平中点钳位逆变器的研究[J]. 电测与仪表,2014,(18):104-107+111.
[17] 宋奇吼,刘文安,陈莉,等. 新型三相Z源逆变器的研究[J]. 电源技术,2014,(12):2346-2348+2395.
[18] 宋奇吼,杨飏,童岩峰,徐百钏. 一种模糊电流预测控制算法在永磁同步电机矢量控制上的应用[J]. 微电机,2015,(11):81-84.
[19] 宋奇吼,陈志辉,施树荣. 四相双凸极发电机的相磁链模型仿真方法研究[J]. 微电机,2015,(4):34-37.
[20] 宋奇吼,陈莉,杨飏. 一种新型Z源逆变器拓扑结构的研究[J]. 电气化铁道,2016,(6):17-20.
A new type of switch coupled induction quasi-Z-source inverter is put forward, with realizing of dramatic increase of inverter output voltage under conditions of same input voltage and shoot-through duty ratio. The paper analyzes the working mechanism, boosting characteristics and control strategies of new topology, verifies the feasibility of new topology by means of simple boosting method and by application of Matlab simulation test.
Quasi-Z-source inverter; switch coupled inductance; voltage boosting capability
10.19587/j.cnki.1007-936x.2017.05.007
U223.5
A
1007-936X(2017)05-0026-05
宋奇吼.南京铁道职业技术学院电力工程学院,教授;刘文安.国网山东省电力公司淄博供电公司,工程师;陈 莉,杨 飏.南京铁道职业技术学院电力工程学院,助教。
(江苏省高等职业院校专业带头人高端研修资助项目,2016TDFX005。)
2016-12-29
