飞行器质心横偏量测量方法及误差分析
2017-11-08卢江仁石成英王国亮
卢江仁,石成英,王国亮
(火箭军工程大学,西安 710025)
飞行器质心横偏量测量方法及误差分析
卢江仁,石成英,王国亮
(火箭军工程大学,西安 710025)
基于一体式质量特性参数测量平台,通过对横向质心和形心的测量计算,推导了飞行器质心横偏量的计算方法,分析了设备初始不平衡量、刀口摩擦系数、传感器刚度、主轴回旋精度及侧向间隙对测量精度的影响,并对其所引起的测量误差进行了计算。结果表明,主轴回转精度及侧向间隙是影响系统误差一个较重要的参数,减小产品质心高度与主支撑轴承跨度比及提高轴承侧隙与回转精度是减小该项误差的有效途径,而传感器刚度对测量误差影响可以忽略。
质心横偏量测量;形心测量;误差计算
在航空航天、武器工程等领域飞行器的质量特性参数对飞行器在飞行过程中的姿态控制、飞行轨迹规划及再入精度等有着至关重要的作用;为了实现飞行器飞行过程中高精度的姿态控制,需要对其质量特性参数进行准确测量。其中质心参数为飞行器的设计、计算、飞行轨道控制、姿态控制等提供了重要参考,是性能评价的核心指标。对于具有规则外形的中、小型产品测量来说,现有的测量手段和测量设备基本能够满足要求;然而,对于质量大、外形不规则的物体来说,现有测量结果却不尽如人意[1-4]。随着服役环境越来越苛刻,飞行器的飞行姿态及稳定性的要求不断提高,内部布局越来越复杂、精密,对其整体质量特性参数的理论计算难以达到实际需求,对其质量特性参数进行实测成为研制、生产环节中必须的内容[5]。
1 质心横偏量的测量方法与设计
质心横偏量是指产品横向质心相对于横向形心的距离在垂直于产品轴线的平面上的投影长度[6]。该参数的精确测量,对于提高飞行器产品性能及飞行可靠性是十分重要的。质心横偏量的测量分为横向质心测量和形心测量两个部分。对于质心的测量,目前主要用三点法进行测量,而形心的测量主要是采用类似于圆度仪的测量方法[7]。在已有的测量方法中,质心和形心的测量一般放置在两个测量设备上进行,这种测量方法最大的误差来源在于测量基准不同。要解决此问题,需在原有的质心测量设备基础上,加装一个形心测量设备,使两者的测量基准重合且不发生移动。这样,产品一次安装到位后,便可分别测量质心和形心,且计算得到的横偏量更为精确可靠。
本文基于一体式质量特性参数测量平台分析其质心横偏量的测量与计算,其测量在设备转轴坐标系下进行,首先进行横向质心测量,然后进行形心测量,将测量结果在设备转轴坐标系进行矢量合成,转换到产品坐标系中,即可求得产品坐标系下产品质心横偏。
1.1 横向质心测量
横向质心测量原理如图1所示,OX为旋转轴,转台带动产品转动并沿两侧刀口线摆动,G为弹头质心,M为弹头质量,A、B为两传感器支点,OA=OB=R。
对旋转轴取矩可得:

图1 横向质心测量原理图
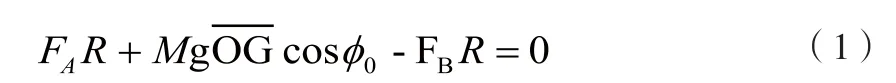
该转台以起始角0φ为起点旋转,每转过一个φ,都可以得到对应的一个:

联立公式(1)、(2)得:
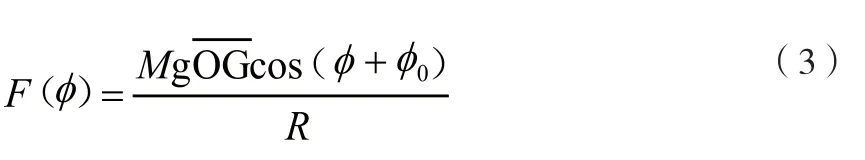
由于质心偏离旋转轴会导致载物盘向单侧倾斜,此时产品已不处于水平摆置,上式求得质心方位会存在一个偏离误差,为消除该误差,通过配平使载物台重新恢复水平状态,使两传感器读数一致,即使配平后的综合质心移回到旋转轴,根据公式(3)找出质心方位后,在对应φ间隔180°处放置相应砝码,使砝码对旋转轴产生的矩等于。考虑到配平砝码的质量和放置方位等因素的影响,需要多次重复上述方法使得最终的配平质量小于某个我们可以接受的误差值。
图2给出了砝码配平过程示意图,设配平时共放置了N块砝码,每块砝码重量为WPi,与OY轴夹角为iφ,配平半径为Ri,按静矩等效可求出等效质量和等效位相(承物盘设计有专用配平槽,使,依据等效质量及位相可以计算出被测体质心相对于旋转轴的位置
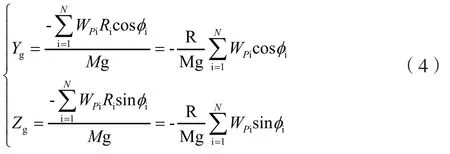
1.2 形心测量
形心测量采用圆度仪测量原理,测量原理图如图3所示。待测产品固定在主旋转台轴系上,轴系绕中心轴转动,位移测量尺测出待测工件表面转动一周的变化量,绕中心轴一周均匀取N组采样值利用最小二乘法拟合圆的圆心位置。
图中不规则截面为待测产品的某一截面,O1为旋转中心轴,O2为该截面的拟合圆心,其直角坐标为(a,b),极坐标为(c,α)。
假设待测产品在该截面拟合圆的半径为R0,则测得的该截面圆周上任一点的值为:
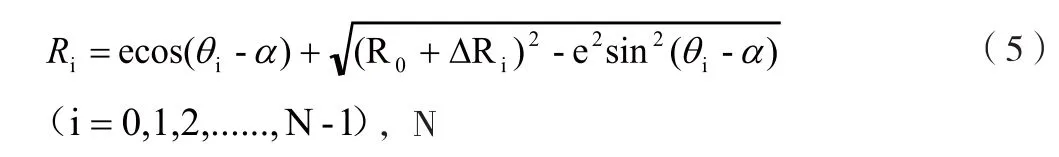
利用以最小二乘法原理为基础的主轴平均回转轴线公式,可解得:
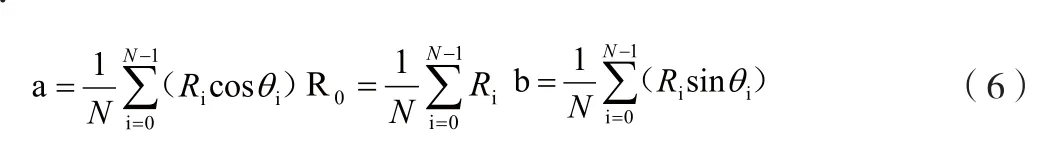
(a,b)即为该圆的圆心。

图2 砝码配平示意图
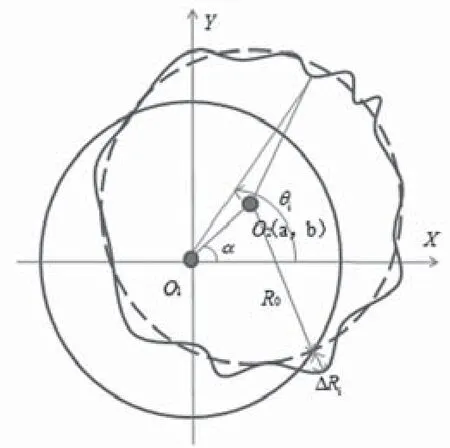
图3 形心测量原理图
选取N个截面进行形心测量,测量特定截面的形心坐标后,就可以用最小二乘法拟合得到整个物体的形心轴线,设物体顶点坐标为O(x0,y0,z0)则:

式中:l、m、n分别为拟合形心轴线L的方向余弦。假设:

形心轴线的拟合可转化为两个平面的拟合,利用最小二乘法拟合原理[8],可先求得两个平面各自的残差平方和:
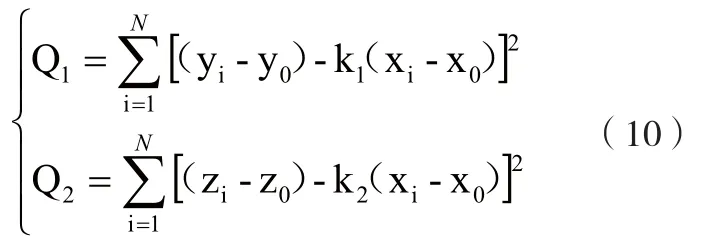
N为沿物体纵轴线方向测量的截面面数。要使残差的平方和最小,只需使:
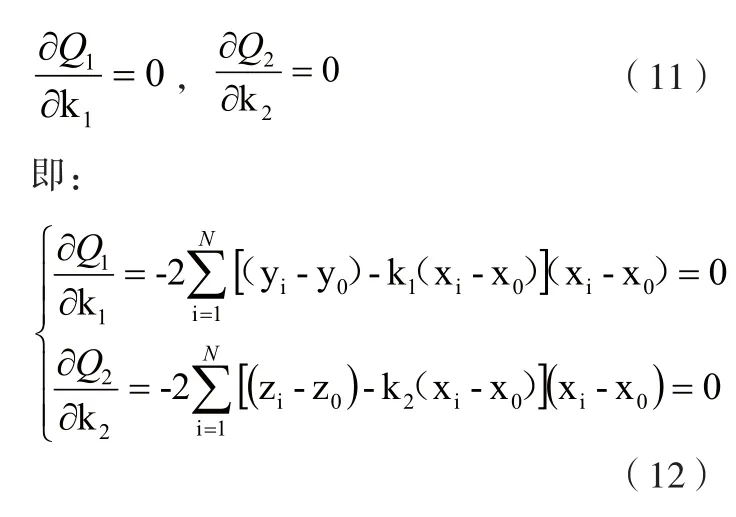
对于特定高度形心的坐标,即可求得测量坐标系中与之对应的特定截面的形心坐标

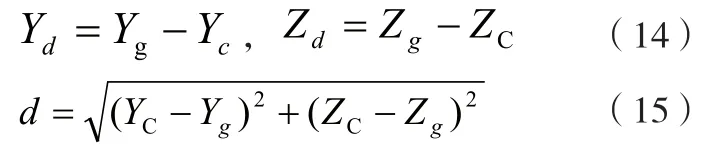
2 误差分析
在实际测量过程中由于设备设计工艺、配平时的不平衡、回旋精度及间隙及传感器本身刚度、刀口摩擦等都会对质心横偏参数的测量带来影响,存在系统测量误差,本文对影响横向质心和形心的误差进行简要分析。
2.1 横向质心误差分析
在本测量台上进行横向质心测量时,其误差来源主要受传感器刚度、设备初始不平衡、刀口摩擦系数和主轴回转精度及侧向间隙影响。
1)配平时剩余不平衡量影响
在分析配平法原理的时候,我们知道了配平最后会留下一个剩余不平衡量ΔWP,它会使横向质心坐标减少一个增量,结合公式(4)分析得其造成的绝对误差为:

经查阅相关数据资料[9],ΔWP为15 g,假设R为600 mm,M为200 kg,可估算得:

从上式中可以看出,减小承力点到承力中心距离和提高配平砝码精度是减小该项误差的有效途径。
2)传感器刚度影响[10]
由于传感器刚度的限制,上述剩余不平衡量ΔWP会引起传感器变形,增加一个偏量。设产品质心高hG,传感器满量程位移ω,量程为Pω,则误差为:

假设 hG为700 mm,ω为1 m,Pω为2940 N可估算得:

适当增大传感器的刚度可以有效降低测量误差量,一般来说,传感器刚度引起的误差很小,一般可以忽略。
3)设备初始不平衡影响
设备测量原理要求设备本身的质心和旋转轴应当重合,即保证测量质心和形心的测量基准相同,实际应用中由于设备不可能绝对平衡,将给结果带来误差。该不平衡量同样涉及到前面论述的传感器刚度和剩余不平衡量,故:

4)刀口摩擦系数影响
由于两刀口会产生一定摩擦力,将形成一定摩擦力矩,设刀口半径为R1,摩擦系数为f,则对的影响为:

减小摩擦系数和刀口半径是减小该项误差的有效途径。
5)主轴回转精度及侧向间隙影响
旋转轴线作为质心的测量基准,若旋转过程中轴线不是理想直线,其摆动量将对测量结果产生影响[9]。设主轴两支撑轴承跨度为hz,轴承侧隙与回转精度造成的轴端跳动为D,产品质心高度为hG,则此项引起的最大误差为:要的参数,减小比和提高轴承侧隙与回转精度是减小该项误差的有效途径。
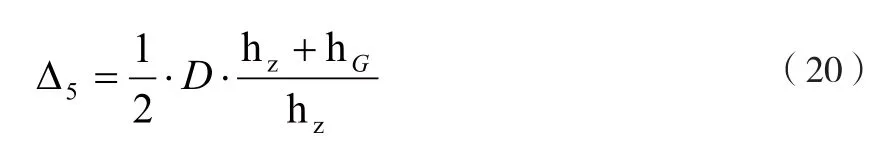
对于被测产品,质心测量误差还应考虑产品质心基准和设备测量基准不重合引起的误差。由于文中主要描述质心位置测量,关注的是测量设备基于自身测量基准的测量精度,这里仅讨论设备自身测量误差。
2.2 形心测量的误差
形心测量的误差来源主要有旋转轴回转精度及轴系侧向间隙、测量尺测点及方向偏离起始轴(OX轴)、测量角度α、测量尺读数精度等。其中主轴回转精度及侧向间隙对形心测量误差的相关影响与对横向质心测量的影响是一致的,其误差计算可以沿用式(20),在此不再详叙,下面主要分析测量点及测量角度及测量尺读数精度对测量的影响。
1)测量尺测点及方向偏离起始轴(OX轴)
这种偏离是在立柱系统直线导轨、丝杠与水平面的
主轴回转精度及侧向间隙是影响系统误差一个较重垂直度、相互平行度以及测量尺的平行度共同作用下引起的,分为两种典型情况,如图4所示:
由于测量尺与OX轴夹角很小,其误差主要由测点处偏离OX轴的偏离量引起,设偏离量为δ,则由δ引起的测量误差为
,设该截面处半径为R,有:
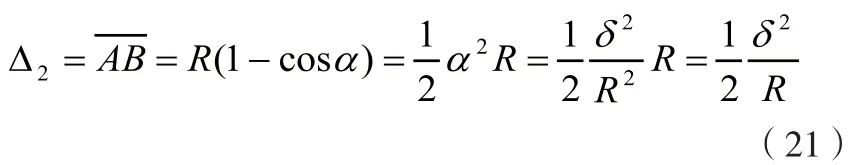
2)角度测量影响
角度有一个初始值的误差,即读的零点与OX轴不重合,该影响其实质同样可以等同测量头产生一个系统偏差δ,初始读数误差为‘α。

在测量系统中,角度测量引起的误差较小,可通过减小转盘精度来减小误差,效果明显。
3)测量尺读数精度影响
在本质量特性参数测量系统中,测量尺主要用光栅尺作为传感元件,其误差为,形心总误差为:

横偏量误差不大于上述质心误差和形心误差之和,即:

3 结语
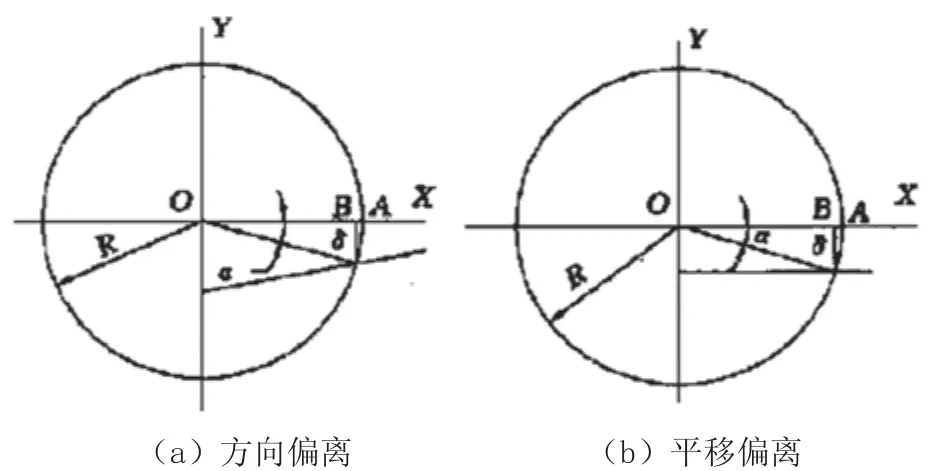
图4 测量尺引起的误差示意图
从质心横偏量测量方法的设计思路入手,以测量方法和测量原理相结合的方式,推导横向质心坐标,通过圆度仪原理推出形心坐标,给出了质心横偏量的计算公式。对影响横向质心测量和形心测量的误差因素进行了分析,计算了横向质心测量误差、形心测量误差和横偏量误差,并给出了减小误差的方法,分析认为该质量特性参数测量仪在测量质心横偏量时,误差满足设备精度要求。
[1]王秋晓,王迎.飞行器质量特性参数测量[J].重庆大学学报, 2011,34(12):23-28.
[2] Gobbi M, Mastinu G, Previati G, et al. A method for measuring the inertia properties of rigidbodies[J].Mechanical Systems and Signal Processing,2011,35:305-318.
[3] 候悦民,季林红,金德闻.小卫星动平衡研究——质心偏差对姿态控制精度的影响[J].导弹与航天运载技术,2003,(4):12-16.
[4] 吴斌,王海峰,马贵贤.大质量飞行器质心测量方法.[J].宇航计测技术,2007,27(6):28
[5] 鲁四平.导弹产品质量特性参数测量方法的研究[J].机械强度,2002,24(4):623-625.
[6] 李顶根.新型立式动平衡机的研制与工件动不平衡的测量[D].湖北:华中科技大学,2004.
[7] 张立明.质量质心及转动惯量一体化测试系统设计[D].哈尔滨工业大学:航天学院,2013:3-6.
[8]薛丽红.三维空间点中基于最小二乘法的分段直线拟合方法[J].齐齐哈尔大学学报,2015,31(4):84-85.
[9]张磊乐,卢志辉,孙志扬,李祥云,费星如.大长径比构件转动惯量卧式测量及误差分析[J].计量与测试技术,2008,35(8):67-68.
[10] 严晖.主轴回转误差理论中几个问题的探讨[J].西安交通大学学报,1983,5(17):85-89.
Error Analysis and Measurements for the Lateral Eccentricity of the Aircraft's Barycenter
Lu Jian-gren, Shi Cheng-ying, Wang Guo-liang
(The Rocket Army Engineering University. Xi'an 710025)
The calculation methods for lateral eccentricity of barycenter on the aircraft was deduced by calculating the lateral center of mass and centroid of the aircaft on the special appliance for the mass property of some kind of strategic missile warhead made by ZhengZhou Research Institute of Mechanical Engineering. The factors which influencing measurement accuracy was researched such as the initial unbalance of the equipment, the friction coefficient of the knife edge, the sensors'stiffness, the cyclotron accuracy of the mainshaft and the lateral gap and so on. The error which induced by above factors was calculated at the same time. The research indicated that the cyclotron accuracy of the mainshaft and the lateral gap are the important parameter which effect the systematic error, reducing proportion of the axial center of mass to the span of the mainshaft and improving the cyclotron accuracy of the lateral gap were effective method to reduce the error. however, the influence of the sensor's stiffness can be neglected.
the Lateral Eccentricity of Barycenter; Centroid Measurment; Error Analysis
TH69
A
1004-7204(2017)04-0113-05
卢江仁,(1980-),研究领域为战斗部工程技术。
