永磁直线同步电机滑模控制系统*

车志远, 陈军强, 杨春雨, 卜淑萍

(1. 中国矿业大学 信息与电气工程学院，江苏 徐州 221008；2. 国网青海省电力公司 海南供电公司，青海 海南藏族自治州 813000)

永磁直线同步电机滑模控制系统*

车志远1, 陈军强2, 杨春雨1, 卜淑萍1

(1. 中国矿业大学 信息与电气工程学院，江苏 徐州 221008；
2. 国网青海省电力公司 海南供电公司，青海 海南藏族自治州 813000)

设计了一种基于滑模变结构的永磁直线同步电机(PMLSM)矢量控制系统。从直线电机的基本工作原理出发，通过坐标变换，建立PMLSM在两相同步旋转正交坐标系上的数学模型。基于滑模变结构和李雅普诺夫稳定性理论设计转速调节器，组成PMLSM滑模控制系统。为了验证该控制系统的有效性，在MATLAB/Simulink平台下搭建系统的模型并进行仿真。仿真表明，该控制系统具有很强的鲁棒性。

永磁直线同步电机；滑模变结构；李雅普诺夫稳定；鲁棒性

0 引 言

与旋转电机相比，三相交流永磁直线同步电机(Permanent Magnet Linear Synchronous Motor,PMLSM)因具有结构简单、过载能力强和进给加速度大等特点而被广泛应用于高速、超高速和精密加工等场合[1]。此外，直线电机无需中间传动装置便能产生直线运动，因此取代了传统的“旋转电机+滚轴丝杆”的形式[2]。但是，PMLSM的数学模型是一个非线性、高阶和强耦合的多变量系统，其分析与求解相当复杂，需进行简化并对其研究新的控制方法[3]。

矢量控制的基本思想就是通过坐标变换[4]，先在两相同步旋转正交坐标系中得到直线电机的动态方程。然后，仿照直流电机的控制方法，将三相电枢电流解耦为互不影响的直轴和交轴分量，并对电机输出的电磁力矩进行控制。传统的PID闭环控制方法虽然可以使伺服系统获得一定的控制精度，但系统的响应速度较慢且对参数摄动及外部扰动的鲁棒性不强[5]。滑模变结构作为一种特殊的非线性控制技术[6]，在系统的动态运行过程中，根据当前的偏差及其各阶导数等，使控制量有目的地切换，迫使系统按照期望的状态轨迹运动。将其应用到电机控制领域后，控制系统具有动态响应速度快、对参数摄动及外部扰动鲁棒性强，以及易于设计与实现等诸多优点[7]。

本文从直线电机的基本工作原理出发，通过坐标变换得到PMLSM在两相同步旋转正交坐标系中的数学模型。之后，应用滑模变结构和李雅普诺夫稳定性理论设计转速控制器，构成了PMLSM滑模控制系统。最后，通过MATLAB/Simulink平台搭建系统的模型并进行仿真，从而验证该控制系统的有效性和鲁棒性。

1 PMLSM的数学模型

PMLSM的物理结构是由永磁同步旋转电机演变而来的，其数学模型也可由其得到。

1.1PMLSM的基本工作原理

将永磁同步旋转电机径向剖开，并沿着圆周展开成直线，便得到PMLSM。相应地，旋转电机的定子和转子分别变成直线电机的初级和次级。由稀土永磁材料钕铁硼组成的次级(定子)永磁体产生励磁磁场，当初级(动子)电枢绕组通以三相对称正弦交流电后，形成气隙行波磁场(呈正弦分布)，永磁体产生的励磁磁场与行波磁场相互作用便会产生电磁推力，从而驱动电机的动子作直线运动。其工作原理图如图1所示。

图1 PMLSM工作原理图

1.2PMLSM数学模型

PMLSM的动态模型由磁链方程、电压方程、电磁推力方程和运动方程组成，通过坐标变换，可以得到三相PMLSM在两相同步旋转正交dq坐标系上的数学模型。

在旋转坐标系dq中，初级磁链方程如式(1)所示:

式中:Ld、Lq，id、iq——d、q轴的电感和电流；

ψf、ψd、ψq——永磁体磁链和d、q轴磁链。

电压方程如式(2)所示：

式中:ud、uq——d轴和q轴的电压值；

R——定子绕组的电阻值；

ω——转子的角速度；

p——微分算子,p=d/dt。

电磁推力如式(3)所示：

式中:Fe——电磁推力；

p——电机的磁极对数；

τ——磁极的极距。

PMLSM的运动方程如式(4)所示:

式中:M——载体质量；

v——直线电机的速度；

Fe——电磁推力；

B——粘滞摩擦因数；

FL——负载转矩(假设为恒转矩负载)。

由于PMLSM的气隙较大，所以在理想条件下假设直轴和交轴电感相等，以简化电机的数学模型，即假设Ld=Lq=L。同时，为了实现变量间的解耦，应用矢量控制的思想，使电磁推力正比于交轴电流分量的大小。此外，由于励磁磁场是由次级永磁体产生的，并且其大小几乎恒定，故将直轴电流分量的给定值设定为零[8]。最终，简化后的PMLSM在旋转正交dq坐标系下的状态方程如式(5)所示:

其中:

式中:KF——电磁推力系数。

2 PMLSM滑模控制系统设计

由于滑模变结构控制是根据系统状态误差及其导数设计滑模面(滑动模态的设计与被控对象的参数和外部扰动无关)，并通过控制量的来回切换迫使系统状态始终沿着滑模面滑动，所以可应用于电机控制系统中。

2.1PMLSM滑模控制系统原理

传统的PMLSM矢量控制系统是通过反馈获取电机的实际信号，并根据给定值和系统输出的偏差计算控制量，进而消除其误差，属于PID闭环控制[9](基于误差来消除误差)。本文从直线电机的数学模型式(5)出发，应用滑模变结构设计控制器，构成了PMLSM滑模控制系统。其原理图如图2所示。

图2 PMLSM滑模控制系统原理图

图2中，根据给定转速与直线电机实际转速之间的误差，滑模控制器计算得到交轴电流的给定值。同时，经过电流互感器和坐标变换得到的直轴和交轴电流值分别与给定值比较，并通过励磁电流调节器和力矩电流调节器分别得到直轴和交轴的电压值，再经过由旋转向静止的坐标变换得到空间矢量脉宽调制器的输入电压，最后将驱动信号输入到逆变器便能产生直线电机所需的供电电压，从而实现对直线电机转速的控制。

2.2滑模变结构控制器的设计

基于滑模变结构在PMLSM矢量控制中的应用，其控制器设计如下。

假设给定速度vd为常值，定义如式(7)所示的跟踪误差e(t)。

针对跟踪系统，设计滑模函数s(t)如式(8)所示。

式中： 参数c必须满足Hurwitz条件，即c>0。当系统状态达到进入滑模面后，满足s(t)=0，那么，根据式(8)可得，误差e将以1/c为时间常数而指数趋近于零。

为了满足滑模变结构控制的基本条件(滑动模态存在、滑动模态能达和滑动运动稳定)，定义李雅普洛夫函数V(s)如式(9)所示。

则

由直线电机数学模型式(5)的第3和第4个方程可得式(11)。

联立式(10)和式(11)可得式(12)。

滑模变结构控制采用等效控制法，控制量u(t)的表达式如式(13)所示。

式中:ueq(t)——滑模等效控制部分，用于控制系统的确定部分。

因此，根据式(12)可得式(14)。

为了削弱滑模变结构固有的抖振现象，采用指数趋近律[10]，选择式(15)所示的滑模切换量us(t)，进而控制系统的不确定部分。

式中： sgn(s)为符号函数，η>0且k>0，切换项ηsgn(s)为鲁棒项，通常用于克服外部干扰FL，从而使控制系统具有很强的鲁棒性。

联立式(13)～式(15)，可得控制量u(t)的表达式如式(16)所示。

联立式(12)和式(16)，可得式(17)。

由式(8)和式(17)可知，该控制系统满足稳定性条件，且系统是渐进稳定的。

3 系统建模与仿真

为了验证PMLSM滑模控制系统的有效性，本文利用MATLAB/Simulink仿真平台搭建系统模型并进行仿真。PMLSM的参数和图2中控制器的参数设置如表1和表2所示。

表1 电机参数设置

表2 控制器参数设置

PMLSM滑模控制系统的仿真结果如图3～图5所示。图3为PMLSM三相定子电流。由图3可知，当直线电机进入稳态后，其电流大小接近零，加上负载后，其变化曲线为三相对称正弦交流电。图4为给定转速(虚线)和电机的实际转速(实线)。从图4可知，在0.35 s给定转速从5 r/min变化到10 r/min，而直线电机的实际转速可以实现无超调地跟随给定值的变化而变化。为了验证该控制系统的鲁棒性，在0.75s时刻，给直线电机增加一个2 000 N·m的负载扰动。由图4可知，采用滑模变结构控制的PMLSM系统在0.75 s时刻，其转速稍微出现超调，之后很快进入稳态，并且不存在稳态误差。可见，该控制系统对外部扰动具有很强的鲁棒性。PMLSM的电磁推力变化曲线如图5所示，根据电机的运行特性及图5可知，当对电机不施加负载而进入稳态时，其电磁推力保持为零。在外加负载扰动时，电磁推力可以克服其对电机系统性能的影响。

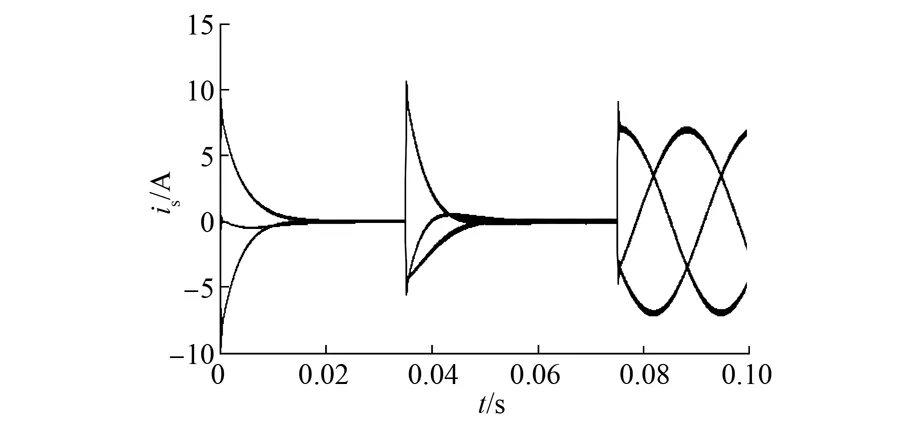
图3 定子电流

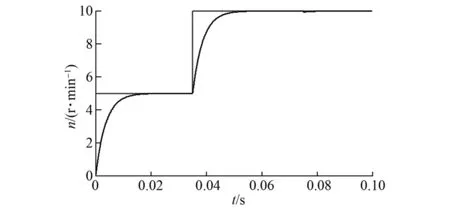
图4 电机转速

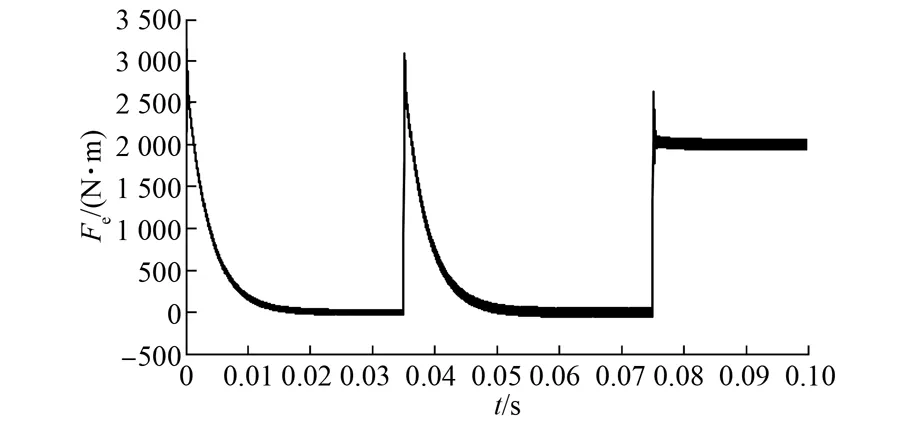
图5 电磁转矩

4 结 语

本文介绍了一种将滑模变结构控制应用到PMLSM矢量控制系统中的方法。该方法使用滑模变结构控制器作为转速调节器，同时，为了削弱滑模变结构控制固有的抖振现象，采用了指数趋近律和李雅普洛夫稳定性理论设计控制量。仿真结果表明，PMLSM滑模控制系统不仅动态响应速度快，而且对外部扰动具有极强的鲁棒性，具有很强的工程实用价值。

[1] ROTARIU I, STEINBUCH M, ELLENBROEK R. Adaptive iterative learning control for high precision motion systems [J]. IEEE Trans on Control Systems Technology,2008,16(5): 1075-1082.

[2] 韩明文,刘军.基于积分分离的永磁同步直线电机PID控制系统[J].电机与控制应用,2013,40(1): 22-24.

[3] SUN X C, QIN H C, CHEN J K. Research on application of fuzzy PID control in linear servo system[J]. Applied Mechanics & Materials,2013,389: 556-562.

[4] 陈伯时,阮毅.电力拖动自动控制系统[M].北京:机械工业出版社,2012.

[5] 金建勋,郑陆海.基于SVPWM的PMLSM控制系统仿真与实现[J].智能系统学报,2009,4(3): 251-257.

[6] 朱晓虹,张广明,梅磊,等.基于滑模速度控制器的PMSM无速度传感器控制研究[J].电机与控制应用,2016,43(1): 1-6.

[7] 赵信杰,李锐华,胡波.无速度传感器的永磁同步电机滑模控制[J].电机与控制应用,2012,39(1): 22-25.

[8] 孙立香,单秀文,靖文.基于SOA的PMLSM进给系统PID参数优化[J].微特电机,2016,44(11): 62-65.

[9] CHEN P, ZHENG J. PMLSM servo system design and implement based on DSP28335[J].Modular Machine Tool & Automatic Manufacturing Technique,2013,4(1): 80-83.

[10] 刘金锟.滑模变结构控制MATLAB仿真[M].3版,北京:清华大学出版社,2015.

PermanentMagnetLinearSynchronousMotorControlSystemBasedonSlidingModeVariableStructure*

CHEZhiyuan1,CHENJunqiang2,YANGChunyu1,BUShuping1

(1. School of Information and Electrical Engineering, China University of Mining and Technology,Xuzhou 221008, China;2. Hainan Power Supply Company, Qinghai Provincial Power Company of State Grid,Tibetan Autonomous Prefecture of Hainan 813000, China)

A permanent magnet linear synchronous motor (PMLSM) vector control system based on sliding mode variable structure was designed. Proceeding from the basic work principle of the PMLSM, and then according to the coordinate transformation, the mathematical model of it is established in the two phase synchronous rotating orthogonal coordinate system. The speed regulator was designed based on the sliding mode variable structure and Lyapunov stability theory, which was composed of the PMLSM vector control system based on sliding mode variable structure. In order to demonstrate the effectiveness of the control system, the model of whole system was built and carried out based on the MATLAB/Simulink. Simulation results verified the control system had strong robustness.

permanentmagnetlinearsynchronousmotor(PMLSM);slidingmodevariablestructure;Lyapunovstability;robustness

国家自然科学基金项目(61374043)

车志远(1993—)，男，硕士研究生，研究方向为电机控制系统设计。

TM 301.2

A

1673-6540(2017)10- 0008- 05

2017 -03 -06