电力系统连锁故障预警模型研究
2017-11-07余剑波
余剑波
电力系统连锁故障预警模型研究
余剑波
(福建泉州亿兴电力有限公司,福建泉州 362000)
由于连锁故障是电力系统大规模停电事故的主要原因,所以对电网连锁故障的原理和特性进行深入研究,预警和预防系统可能发生的大事故,对促进电网运行可靠性的提升意义重大。本文通过总结前人的经验,将分裂技术应用域电网大规模连锁故障的蒙特卡洛仿真中,提高了系统的仿真效率。可以快速地发现电网中的重点负荷线路,从而可以进行有针对性的扩容,也为电网调度运行调整提供了依据。
电力系统;联锁故障;预警模型
电力系统的轻故障极少造成严重的停电事故,严重的事故往往都是电网的连锁故障导致事件逐步升级而造成。连锁故障出现的可能性虽然微乎其微,但其造成的损失却无法估计,因此,在进行系统可靠性评估过程中必须对小概率事件发生的可能性进行评估[1]。故障的连锁会导致系统故障不断升级,可能导致某些线路或设备的负荷过高,这种情况下一些小概率故障发生的可能性会明显提高。如果调度监控人员对系统的实际运行状态认识不清,忽略了不正常的系统扰动,则很容易导致严重的停电事故,而如果对一些正常情况采取的措施过于保守,则系统的经济运行难以保证。因此提前对连锁故障发生的系统状态进行分析,通过仿真评估大规模停电事故的概率,是十分关键的[2]。蒙特卡洛仿真是连锁故障评估的有效手段,传统的蒙特卡洛仿真需要大量的仿真循环才能获得理想的大规模停电事故的结果,这个过程耗费了大量的系统资源。本文用分裂技术对蒙特卡洛仿真进行了改进,使小概率事件的仿真速率大大提高,从而可以快速地发现重点线路,采取必要措施进行预防[3]。
1 分裂技术的模型
1.1 分裂技术的概述
分裂技术将小概率事件看作若干条件概率事件的集合。在确定的事件仿真中,小概率事件发生的概率等于这些条件概率相乘的结果[4]。分裂技术的原理如图1所示。

图1 分裂技术的原理示意图
如图1所示,轴为系统发生故障的等级。从0=0进行仿真,表示发生小概率事件的阈值。把仿真过程按照故障等级划分,即0=0<1<…<L=共个区间。将每个级别进行独立仿真,从分裂点为起点模拟运行。



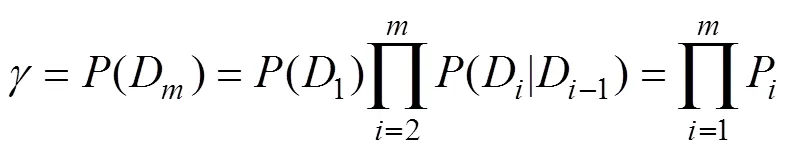
分裂就是对事件D在D-1条件下进行反复仿真,对每个条件单独计算概率。
1.2 分列技术的最优解
分裂样本数量和分裂层级的选择是分离技术的重点。对于样本数量的选择,可以通过最优分裂进行解决[5]。


选取每区间仿真的最优次数N,使得小概率事件的发生概率获得最小方差,即

则最优次数的解为
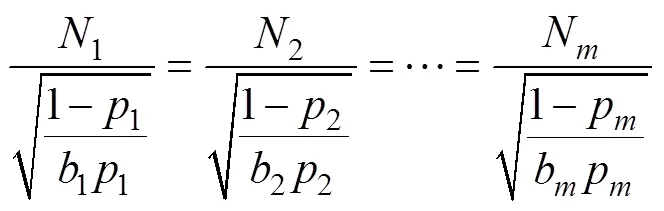
b和决定了N的最优解。当偏小时,仿真次数应相应增加,这样可以降低仿真成本。
对于仿真层级的选择,假定L是最高等级的故障,在每层仿真到下层的概率和每层的仿真次数都相等时,则可获得最优的层级选择方式。设定仿真初始阶段到最终层级的概率为=(D)。求取使得估计值方差最小的层级数的值。
由于
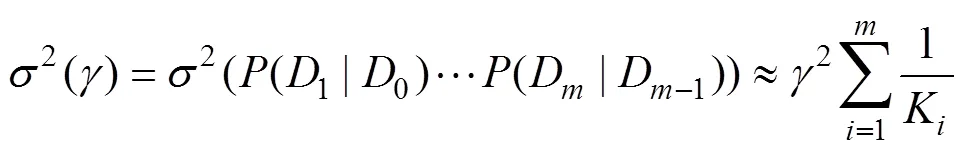
式中,K是层仿真中出现等级L故障的次数,由于L和=(D)都是固定的,则有

限定条件为
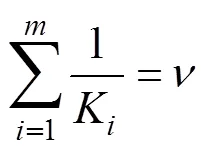
其中,是常数,则有

其限定条件为
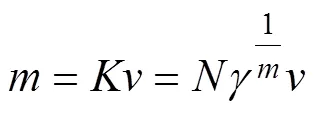
则有

对上式的进行微分,则有

因此,采用四舍五入的方法对取整则可得出最佳分裂层数。
2 分裂技术在电力系统连锁故障预警的应用
在连锁故障预警模型中,不仅要关注不同负荷情况下系统临界状态的变化趋势,还要分析重要的小概率事件。本文将故障严重程度用切负荷量来衡量,研究利用最优潮流的蒙特卡洛仿真模型对切负荷量进行仿真[6]。
2.1 大规模停电事故概率和故障链的仿真
研究IEEE 30节点系统利用分裂技术进行大规模连锁故障的仿真,IEEE 30系统结构如图2所示。负荷削减量和总负荷的比值是分析故障严重程度的重要标准,假设层数为5,限定值设为L=[0.01 0.10 0.20 0.35 0.50]。假设仿真数量为104,每层仿真概率和计算成本均相同,则每层的仿真次数相同。IEEE 30系统的装机总容量为350MW,其负荷起始值为200MW,占装机总容量约57.14%,下面我们对负荷削减量超过50%的连锁故障概率进行计算。
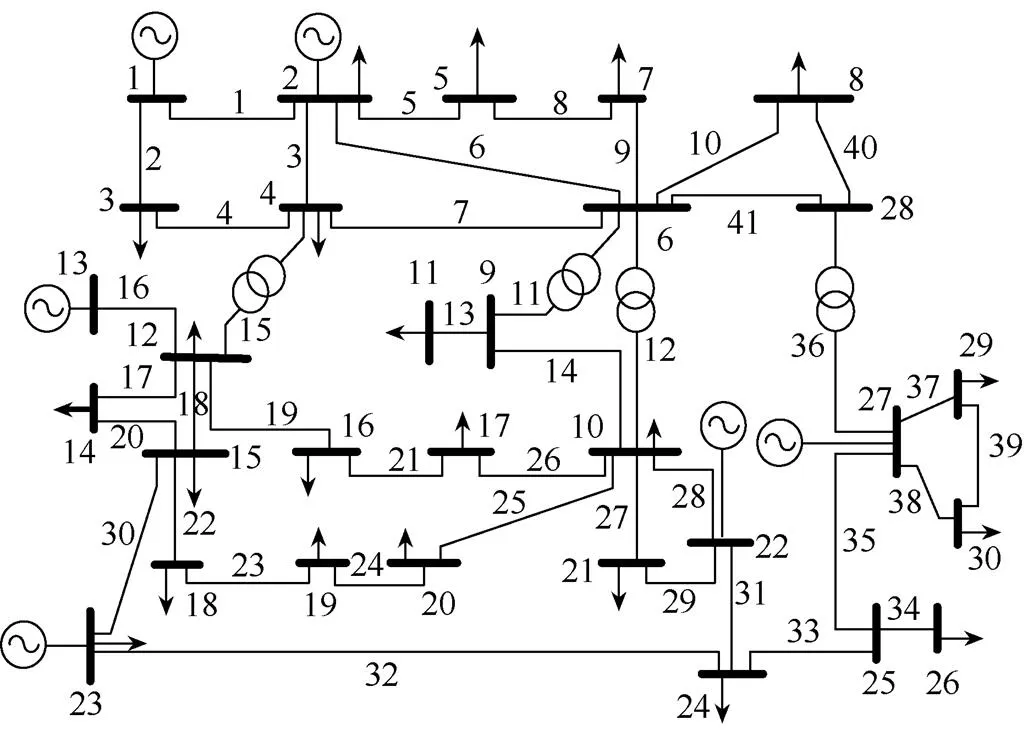
图2 IEEE 30系统结构
首先对第一层级进行仿真,产生初始故障并导致重负荷线路连锁故障的线路自由选取,仿真2000次,负荷削减量超过限定值并可能导致大规模停电故障的次数为29,数据信息见表1。

表1 第一层级仿真切负荷量达到阀值的部分故障
表1记录了部分故障情况,从表中数据可以看出,线路31,32,33出现了初始故障,且负荷削减量为22.05MW,高于层级限定值,同时造成线路41负荷过大,有几率导致严重的连锁故障,因此选择这一状态当成下层仿真的起始状态元素进行保存。表中的“→”表示故障发生的次序,如线路10的故障引起线路40负荷达到限定值,线路发生故障的概率加大,虽然线路10的切负荷在限定范围以内,但其连锁故障仿真的切负荷达到34.861,超过限定值。
我们将以上全部故障状态作为下一层仿真初始状进行执行连锁故障仿真,得出超过第二层阀值的故障状态为157次。用相同的方法利用仿真求得3、4、5层超过阀值的次数分别为10、583、12,则系统出现切负荷超过50%的连锁故障的概率为

可见在使用分裂技术后,只仿真了105次,就发生了12次切负荷超过50%的连锁故障,而理论上需要仿真108次才会发生一次该类故障,仿真效率得到极大改善[7]。最后得出大规模连锁故障链见 表2。

表2 切负荷量达到50%的故障链
以第二条故障链为例,可以采用将其在IEEE 30结构图中进行分析。可以看出,初始故障在线路15、16中出现,造成13节点的发电机无法继续向系统供电,为维持系统负荷平衡,其他发电机会提高功率输出,导致13线路的潮流过大引起线路故障,随后其他线路也因此陆续过载断开。当线路10和40断开后,节点8作为系统中负荷最大的节点,失去供电电源,整个系统受到严重影响,线路15、16、21、23、30陆续断开,节点12、14、15、16、18也先后失去负荷。导致最终的负荷削减量达到117MW,超过总负荷的60%。同时可以发现,节点8负荷比较大,当线路10和40中的任何一个出现问题都会导致另一条线路过负荷,线路的连锁故障发生的可能性相当高[8]。
2.2 系统负荷情况对系统大规模连锁故障概率的影响
设定外循环次数为40,外循环每次只提高负荷,系统发电机的有功功率最大值335MW,系统总负荷从190MW逐步增加到500MW,内循环取104次,切负荷超过50%的概率趋势图如图3所示。

图3 负荷水平不同严重连锁故障的概率
从图3中可以发现,当线路负荷在300MW以下时,发电机的有功功率充足,即使一些线路断开,也轻易不会造成线路过载的情况出现,切负荷超过50%的概率几乎为0。线路此时的故障多为个别线路故障造成部分负荷节点断开。而当线路负荷超过300MW后,发电机过载,此时个别线路的故障会导致其他线路出现过负荷,这时系统出现严重连锁故障的概率依旧不高,但概率在缓慢升高,逐渐接近临界值。而当系统负荷超过450MW后,系统严重连锁故障的概率随系统负荷的上升快速升高,线路的断开很容易导致切负荷量超过50%。因此,维持系统适当的负荷率,对提高系统运行可靠性和经济运行效益是十分必要的[9]。
2.3 重点线路对系统大规模连锁故障概率的影响。
对仿真中出现大规模连锁故障最多的线路进行统计发现,故障次数最多的重点线路为29、28、10、30、40、31、6,出现次数依次为4469、3759、3077、2725、2460、2410、2184。采用任意选取7条线路扩容和对7条重点线路进行扩容两种方式进行仿真,其结果如图4所示。

图4 扩容方式不同大规模连锁故障的概率
从图4中可以发现,任意选取7条线路扩容,线路严重连锁故障的概率变化不明显,而对重点线路扩容改造,可以使严重连锁故障的概率大大降低。主要原因在于重点线路容量增加可以对连锁故障的发生产生抑制作用[10],这一规律可以作为系统调度决策的重要依据。
3 结论
电网的连锁故障是大规模停电的重要原因,对电网连锁故障原理进行深入研究,预防系统大规模停电事故的发生意义重大。本文将分裂技术应用于电网大规模连锁故障的蒙特卡洛仿真中,使仿真效率大大提高。通过系统连锁故障模型,可以快速有效的发现系统中的重点线路,可以通过有针对性的线路扩容,从而有效地提高系统运行的可靠性。
[1] 甘德强, 胡江溢, 韩祯祥. 2003年国际若干停电事故思考[J]. 电力系统自动化, 2004, 28(3): 1-5.
[2] 黄晓晴, 黄勇, 刘辉, 等. 基于动态权重德尔菲法的电力生产事故根本原因重要度分析[J]. 电气技术, 2017, 18(3): 89-93.
[3] 石立宝, 史中英, 姚良忠, 等. 现代电力系统连锁性大停电事故机理研究综述[J]. 电网技术, 2010, 34(3): 48-54.
[4] 刘秋华, 董丹丹, 韩韬. 基于层次分析法的配电网风险评估指标体系研究[J]. 电气技术, 2016, 17(9): 39-42.
[5] 林伟芳, 孙华东, 汤涌, 等. 巴西“11.10”大停电事故分析及启示[J]. 电力系统自动化, 2010, 34(10): 1-5.
[6] 葛少云, 季时宇, 刘洪, 等. 基于多层次协同分析的高中压配电网可靠性评估[J]. 电工技术学报, 2016, 31(19): 172-181.
[7] 印永华, 郭剑波, 赵建军, 等. 美加“8·14”大停电事故初步分析以及应吸取的教训[J]. 电网技术, 2003, 27(10): 8-11.
[8] 丁理杰, 曹一家, 刘美君. 复杂电力网络的连锁故障动态模型与分析[J]. 浙江大学学报: 工学版, 2008, 42(4): 641-646.
[9] 王涛, 李渝, 顾雪平, 等. 电网关键线路序元搜索方法[J]. 电工技术学报, 2016, 31(2): 153-162.
[10] 谭玉东, 李欣然, 蔡晔, 等. 基于电气距离的复杂电网关键节点识别[J]. 中国电机工程学报, 2014, 34(1): 146-152.
Study on Early Warning Model of Cascading Failures in Power System
Yu Jianbo
(Fujian Quanzhou Yixing Electric Co., Ltd, Quanzhou, Fujian362000)
Cascading failure is the main reason for large-scale power system blackout, so the principle and characteristics of the cascading failure of in-depth research, accident early warning and prevention system may occur, to promote the operation reliability of power grid improvement is of great significance. By summarizing the previous experience, the splitting technology is applied to the Monte Carlo simulation of large-scale cascading failures in regional power grid, which improves the simulation efficiency of the system. The key load lines in the power grid can be quickly found, so that targeted expansion can be carried out, and also provides a basis for grid operation adjustment.
power system; interlocking fault; early warning model
余剑波(1981-),男,福建泉州人,本科,工程师,主要从事电气设计及技术服务工作。
