求解多目标最优潮流的改进粒子群优化算法

张 勤 张健美 马 强 王先洪



求解多目标最优潮流的改进粒子群优化算法

张 勤1张健美2马 强1王先洪1

（1. 四川省电力公司南充供电公司，四川南充 637000；2. 四川省电力公司技能培训中心，成都 610071）

本文对多目标最优潮流算法进行了研究，通过运用改进粒子群算法对考虑发电费用和有功网损的多目标最优潮流进行了计算。首先运用模糊集理论对多目标函数进行了处理，使其转化成单目标问题；其次对粒子群算法进行了改进，通过对加权系数和粒子位置变量的改变，避免粒子群在寻优过程中陷入局部最优；运用C均值聚类算法对解集作了聚类处理，使解满足均一化的要求。通过对IEEE系统的测试，证明了本文算法的正确性。

多目标；最优潮流；粒子群优化算法；模糊集理论；C均值聚类算法

最优潮流（OPF）是指当系统的结构参数和负荷都已给定时，调节可利用的控制变量（如发电机输出功率、可调变压器抽头等）找到能满足所有运行约束条件的，并使系统的性能指标（如发电成本或网络损耗）达到最优值的潮流分布。它是典型的多目标非线性规划问题。由于系统中的各个目标大多是相互冲突的，因此要找到绝对的最优解是很困难的。对最优潮流的研究很多[1-7]，这些研究方法大致可以分为两类：①传统的优化算法；②现代智能优化算法。文献[2]对最优潮流模型进行了改进，运用内点法进行最优潮流问题的求解。文献[3]运用改进的粒子群算法进行潮流的最优化求解。文献[4]针对多目标最优潮流问题提出了一种基于Pareto解集的改进粒子群算法，用最优值评估选取法求取粒子和全局最优位置，解决目标函数间可能存在的 冲突。

本文对多目标最优潮流算法进行了研究。首先对目标函数进行模糊化处理，使其转化成求解单目标问题。针对传统的粒子群算法容易陷入局部最小问题，对粒子群的属性更新公式进行了改进，并运用C均值聚类算法对解作均一化处理，提出了求解最优潮流的粒子群算法。

1 多目标最优潮流模型

最优潮流是指在满足电力约束条件下目标函数最小的一种稳定运行状态。根据研究目的和环境的不同，建立的目标函数也有所不同。本文以发电费用最小和有功网损最小建立最优潮流的目标函数。

系统中发电机发电费用为

系统有功网损为

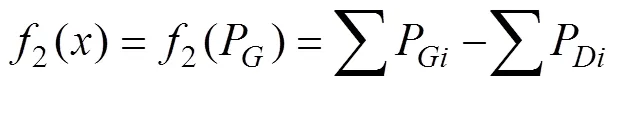
最优潮流的目标函数可以表示为

为了使系统能在安全稳定的环境中运行，系统中的参数还必须满足一定的约束条件，包括等式约束和不等式约束。其中等式约束为电力系统潮流方程，只要潮流计算收敛，等式条件就能得到满足。

不等式约束条件主要指控制可调变量在一定的容许范围内变动，满足电力系统运行的安全性，其中主要的不等式约束包括功率，电压等的约束。

通过以上分析，最优潮流问题即转化为在满足等式和不等式约束条件下，求解目标函数最小值问题。本文将结合粒子群算法对最优潮流模型求解。

2 粒子群优化算法

2.1 粒子群算法的基本模型

在粒子群算法的每一次迭代过程中，粒子群中所有粒子的属性都会根据以下两个式子进行更新，即

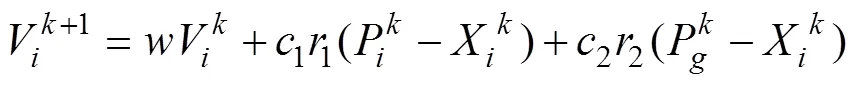
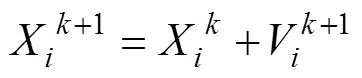
在传统的粒子群算法中，通过改变粒子群的位置和速度不断寻优以找到全局最佳位置。当某个粒子找到当前粒子群所处的最优位置时，其他的粒子将会迅速向它靠拢，这样容易陷入局部最优，使粒子群无法继续在整个空间寻找最优位置。因此，必须采取方法提高粒子群的全局搜索能力。

2.2 加权系数的改变与扰动量的引进

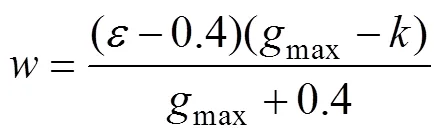
多目标最优问题是一个多峰值的全局最优问题。在寻优的过程中，当粒子群陷入局部最优时，可以对局部最优变量加入新的扰动量，使局部最优量跳出局部的最优点，进行新的全局范围内搜索。

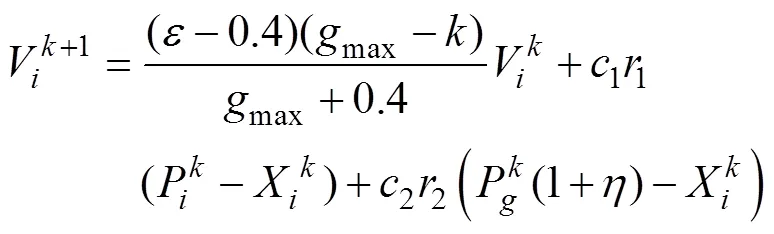
2.3 最优解集的均匀分布性

在粒子群算法解的性能评判标准中，解的多样性和分布的均匀性是评判其性能的标准之一。为了达到这一评判标准，本文采用C均值聚类算法[11]对解作均一化处理。该算法通过反复的迭代计算来修正聚类中心，并以欧式距离作为判断样本隶属的依据。当达到某一个特定的条件或者阀值的时候，结束迭代过程并完成分类。

运用C均值法实现粒子群解集的均匀分布步骤如下：

1）初始化聚类C。

2）根据C均值算法对解集进行分类，并根据式（16）计算出它们的欧式距离。

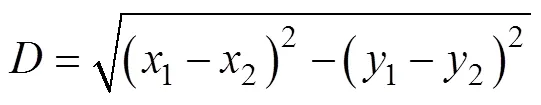
3）对于欧式距离相近的聚类进行合并。

4）反复进行迭代计算，直到聚类数小于需要的聚类数M为止。

5）在各个解的聚类中选择最能代表该聚类的解（即与其他解的欧式距离最小的解）组成新的非支配解集。

3 多目标最优潮流算法

在求解多目标最优潮流问题时，优化的目标不止一个，很难得到一个使各个目标函数都达到最优的解。在运用粒子群优化算法求解时，需要先对目标函数进行单目标处理，而不能直接求解。

根据以上分析，多目标最优潮流的计算步骤如下所示：

1）确定最优潮流的目标函数并运用模糊化处理方法得到隶属函数。

3）在约束条件范围之内随机生成个解。赋予每个粒子在约束范围之内的初始速度和初始位置。

4）根据式（11）和式（12）更新粒子群的速度和位置向量。

5）根据式（19）计算目标函数。

7）判断是否达到了计算的精度或达到循环的最大次数，若未达到，则转入第4）步，否则进入下一步。

8）根据C均值聚类算法对得到的优化解进行均一化处理，并得到最终解的结果。

4 实例分析

为了验证本文所提方法的实用性，文中对IEEE 30节点系统进行了最优潮流计算。系统的基本参数见表1。

表1 测试系统基本数据

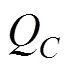
以发电费用和有功网损为优化的目标函数，运用本文算法对潮流进行优化计算，并对比文献[13]的优化结果，最终结果见表2。

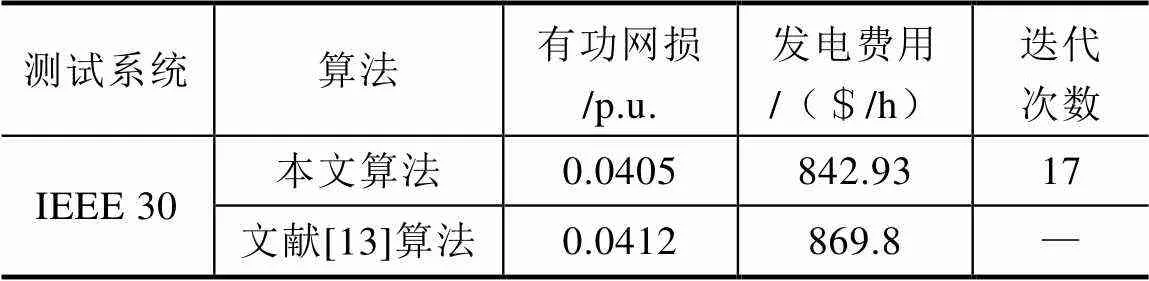
表2 两种优化方法计算结果比较

从表2中的结果可以看出，本文的算法具有较强的寻优能力是可行的。

为了比较单目标最优潮流与本文中的多目标最优潮流的优化性能，文中分别以综合考虑有功网损和发电费用的优化目标和只考虑发电费用最优或只优化有功网损的不同情况进行了优化计算，其计算结果见表3。

表3 系统优化计算结果

根据表3的计算结果可以看出，当单独考虑某一个优化目标时，该目标的优化效果较好，但是非目标项的表现却不是很好。多目标系统兼顾考虑了不同的目标函数，虽然单个目标函数并未达到最优，但是整体的优化效果较好，这样得到的结果将更加有助于网络优化。

从优化过程中迭代的次数来看，多目标系统的迭代次数比单目标系统的迭代次数要多，这是由于多目标系统比单目标系统的变量要多，同时多目标系统在运用粒子群算法求解之前，需要把目标函数进行模糊化处理，转化成单目标系统进行计算，因此其迭代次数比单目标系统有所增加。

5 结论

本文运用改进的粒子群算法对考虑发电费用和有功网损的多目标系统最优潮流进行了计算。把多目标系统目标函数进行了模糊化处理，使其转化成单目标系统。对粒子群算法进行了改进，避免其陷入局部最优，并对最优潮流的算法进行了研究。最后通过对IEEE系统的测试，证明了本文算法的正确性。

[1] 苏申, 阮玉斌, 刘庆珍. 配电网三相潮流计算方法研究[J]. 电气技术, 2017, 18(2): 1-4.

[2] 江全元, 黄志光. 基于功率电流混合潮流约束的内点法最优潮流[J]. 电力系统自动化, 2009, 33(12): 32-37.

[3] 杨波, 赵遵廉, 陈允平, 等. 一种求解最优潮流问题的改进粒子群优化算法[J]. 电网技术, 2006, 3(11): 6-10.

[4] 胡德峰, 张步涵, 姚建光. 基于改进粒子群算法的多目标最优潮流计算[J]. 电力系统及其自动化学报, 2007, 19(3): 51-57.

[5] 刘林, 王锡凡, 丁晓莺, 等. 一种恢复最优潮流可行性的实用方法[J]. 电力系统自动化, 2009, 33(19): 36-42.

[6] 覃智君. 最优潮流的原对偶内点法矢量化实现[J]. 电力系统及其自动化学报, 2009, 21(5): 68-74.

[7] 崔鹏程, 陈明榜, 向铁元. 基于粒子群优化算法与混合罚函数法的最优潮流计算[J]. 电网技术, 2006(30): 192-195.

[8] 马草原, 孙展展, 尹志超. 基于双重混合粒子群算法的配电网重构[J]. 电工技术学报, 2016, 31(11): 120-126.

[9] 赵志刚, 顾新, 李陶深.求解双层规划模型的粒子群优化算法[J]. 系统工程理论与实践, 2007(8): 92-98.

[10] 刘淳安. 一种求解动态多目标优化问题的粒子群算法[J]. 系统仿真学报, 2011, 23(2): 288-293.

[11] 陈柔伊, 张尧, 武志刚, 等. 改进的模糊聚类算法在负荷预测中的应用[J]. 电力系统及其自动化学报, 2005, 17(3): 73-77.

[12] 刘明波, 段晓军. 一种求解多目标最优潮流的模糊优化算法[J]. 电网技术, 1999, 23(9): 23-27.

[13] 乐秀, 覃振成, 尹峰. 基于自适应模拟退火遗传算法的多目标最优潮流[J]. 继电器, 2005, 33(7): 10-15.

[14] 任洲洋, 颜伟, 项波, 等. 考虑光伏和负荷相关性的概率潮流计算[J]. 电工技术学报, 2015, 30(24): 181-187.

[15] 娄刘娟, 金光, 张玲. 基于Matlab的动态潮流研究[J]. 电气技术, 2016, 17(5): 41-44.

The Improved Partical Swarm Optimization Algorthim for Multiobjective Optimal Power Flow

Zhang Qin1Zhang Jianmei2Ma Qiang1Wang Xianhong1

(1. Nanchong Power Supply Company of Sichuan Electric Power Corporation, Nanchong, Sichuan 637000;2. Skill Training Center of Sichuan Electric Power Corporation, Chengdu 610071)

The multiobjective optimimal power flow algorithm is researched in this paper. Using the improved partical swarm optimization algorthim to calculate power flow considering the cost and network loss. The fuzzy set theory is used in multiobjective function processing to make it a single objective. And the partical swarm optimization algorthim is improved through adjusting and particle position variable to avoid being into a local optimal. Using C means clustering algorithm for set esterase processing, and making the solution more satisfying the requirements of the homogenization. The correctness of the algorithm researched in this paper is proved through the IEEE system test.

multiobjective; optimal power flow; partical swarm optimization algorthim; fuzzy set theory; C means clustering algorithm

张 勤（1987-），女，四川省广元市人，工程师，主要从事二次系统检修工作。