认知无线电中下变频信号处理的频谱研究

梁 爽，伍小芹

(1.西安电子科技大学 通信工程学院，陕西 西安 710071；2.海南大学 信息科学技术学院，海南 海口 570028)

认知无线电中下变频信号处理的频谱研究

梁 爽1，伍小芹2

(1.西安电子科技大学 通信工程学院，陕西 西安 710071；2.海南大学 信息科学技术学院，海南 海口 570028)

针对认知无线电中下变频处理中的信号抽取过程对信号频谱的影响进行了研究，信号抽取由积分梳状(CIC)滤波器、半带(HB)滤波器及多相滤波器级联而成，利用傅里叶变换对各环节处理后的信号频谱进行理论推导，得出各级抽取后信号频谱的变化规律及各参数选择要注意的问题。通过实验仿真，对整个抽取系统进行测试，仿真结果表明，采样率为fs的信号经过3级抽取，且抽取倍数为DCIC·DHB·D多相时，输出信号的采样率变为fs/(DCIC·DHB·D多相)，与理论推导结果一致，实现了多速率信号处理。

认知无线电；积分梳状滤波器；半带滤波器；多相滤波器；频谱分析

0 引言

数字下变频技术是认知无线电实现信号多速率处理的关键技术[1]，主要工作是将中频载波上携带的有用信号搬移到基带[2]，频谱搬移是利用信号抽取完成的，先让信号通过积分梳状(CIC)滤波器和半带(HB)滤波器，降低信号的采样率，必要时还要经过多相滤波器，以实现整数倍[3]或非整数倍的采样率变换[4]。

针对采样信号的抽取、内插、抽取和内插结合的分数倍采样率变换的研究有很多[5]，大都是根据多采样率信号处理理论进行相应的讨论，没有讨论多个抽取滤波器的级联。文献[6]给出了一种典型的多速率信号处理结构图，对各环节进行了讨论，但没有形成整个抽取系统，缺少整体可行性分析。文献[7]利用窗函数法和特征滤波器法分别设计半带滤波器，讨论半带滤波器的优化设计问题。根据对文献的分析，缺少对整个多速率信号处理系统整体的设计，单个滤波器容易实现，但在级联时需要考虑相应的问题[8]。本文从认知无线电下变频技术入手，讨论了利用CIC滤波器、HB滤波和多相滤波器级联来实现整数倍或非整数倍采样率变换的结构，结合各滤波器的特征，对各抽取器的关键参数的选择进行了分析，实现了整个系统的整体仿真，完成了多采样率的变换。

1 认知无线电中的下变频技术

认知无线电中数字下变频技术原理[9]如图1所示，硬件处理是对接收到的射频模拟信号进行预处理，得到模拟中频信号，对该模拟信号进行A/D转换，采样得到数字中频信号，假设A/D转换后采样率为fs[10]。将数字中频信号与数控振荡器产生的复向量在正交数字混频器中相乘，产生的信号包含低频和高频频率成分[11]。由于信号采样频率可能会过高，后面的模块无法达到这种速率，所以可以先让信号通过CIC抽取和HB抽取滤波器，降低信号的采样速率，再利用FIR滤波器对信号进行整形，得到基带信号进行后续处理[12]。

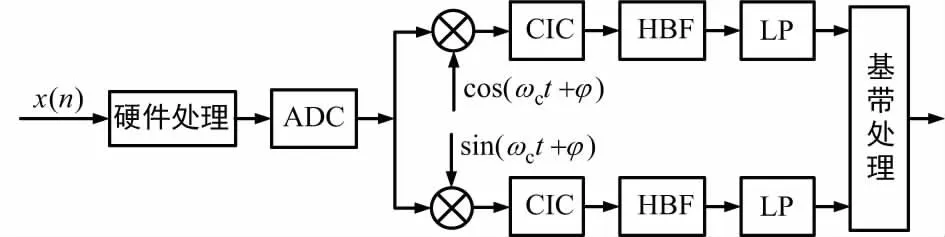
图1 数字下变频技术原理

通过对数字下变频原理及结构的分析，将其中多速率信号处理部分单独整理出一种多速率信号处理结构，为实现整数倍或非整数倍抽取，在结构中加入多相滤波器，如图2所示，整个结构包括CIC滤波器、HB滤波器、FIR滤波器以及多相滤波器，它们在系统中分别有着不同的作用，一起完成信号抽取任务。

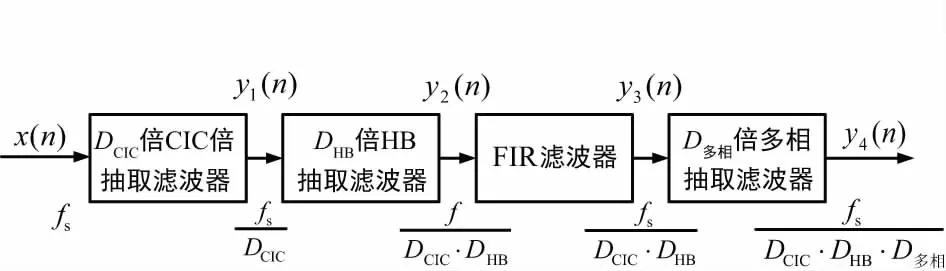
图2 多速率信号处理结构图

2 各滤波器设计及频谱分析

CIC滤波器可实现整数倍抽取，HB实现2N倍的采样率变换，FIR滤波器用来去除HB滤波器过宽的过渡带造成的残留频率[13]，多相滤波器采用分数倍采样率转换，实现非整数倍抽取。下面对CIC滤波器、HB滤波器、多相滤波器的设计及其频谱进行分析。

2.1 CIC滤波器设计及其频谱分析

CIC滤波器的冲激响应为[14]：

(1)

式中，M为滤波器的长度,对应的系统幅频特性为：

(2)

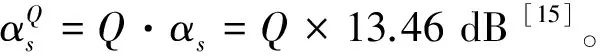
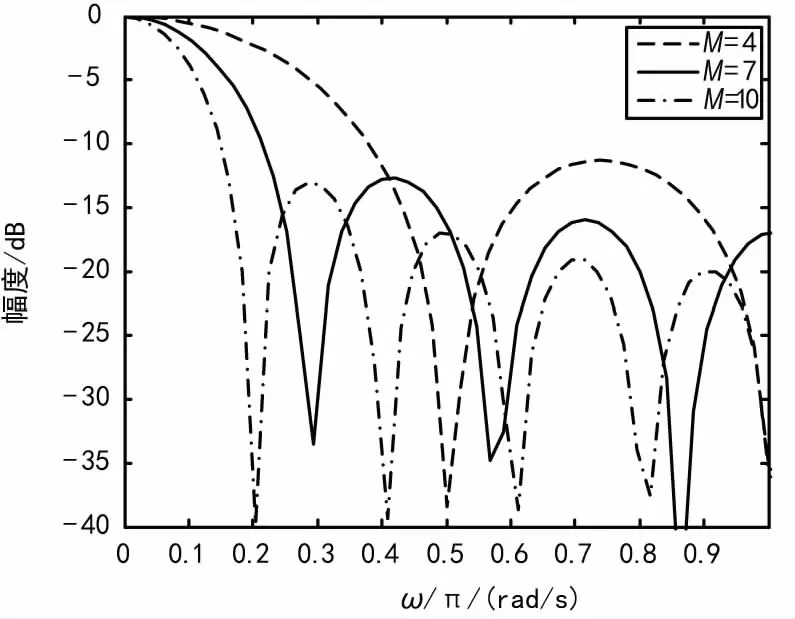
图3 CIC滤波器长度对幅频特性的影响

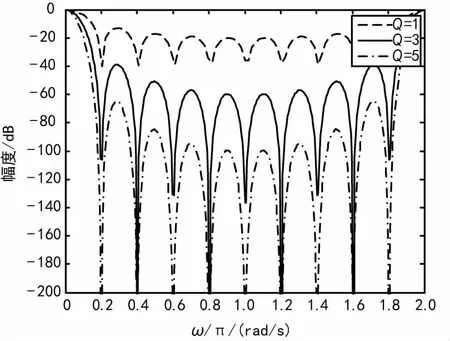
图4 CIC级数对幅频特性的影响

2.2 HB滤波器

HB滤波器是一种特殊的FIR滤波器，要求抽头数N满足N+1是4的整数倍[16]，且其冲击响应在偏移中心点的偶序号点上系数都取零，奇序号点上的系数关于滤波器的中心点呈现偶对称[17]，这些特性使得在实现此类滤波器时节省近一半的乘法器数量。

不同阶数的HB滤波器的幅频特性如图5所示，HB滤波器的过渡带宽与其阶数成反比，阶数越小，通带衰减快，同时过渡带越宽，在多采样率系统中会加大频谱混叠影响。

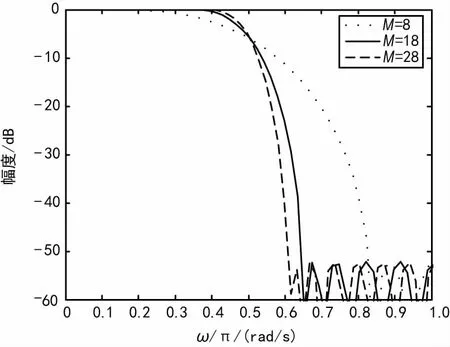
图5 不同阶数的HB滤波器幅频特性

2.3 CIC滤波器与HB滤波器比较

作为抽取滤波器，CIC滤波器与HB滤波器都能够完成整数倍抽取，但是2种滤波器各有优点。CIC滤波器只有加法器没有乘法器，与一般的线性滤波器、非线性滤波器相比节省计算存储存储空间。HB滤波器节省一半的计算量，适合实时性处理[18]。利用Matlab仿真比较两滤波器的计算效率，相同输入信号，相同倍数抽取，Matlab仿真结果和仿真所用时间分别如图6和图7所示。

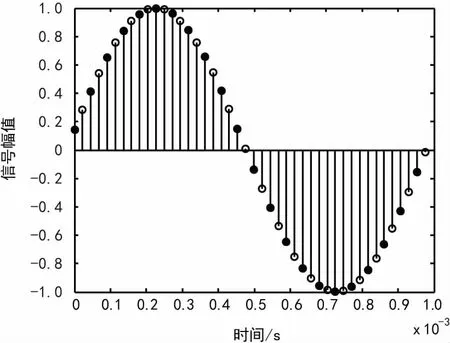
(a) CIC两倍抽取时域结果

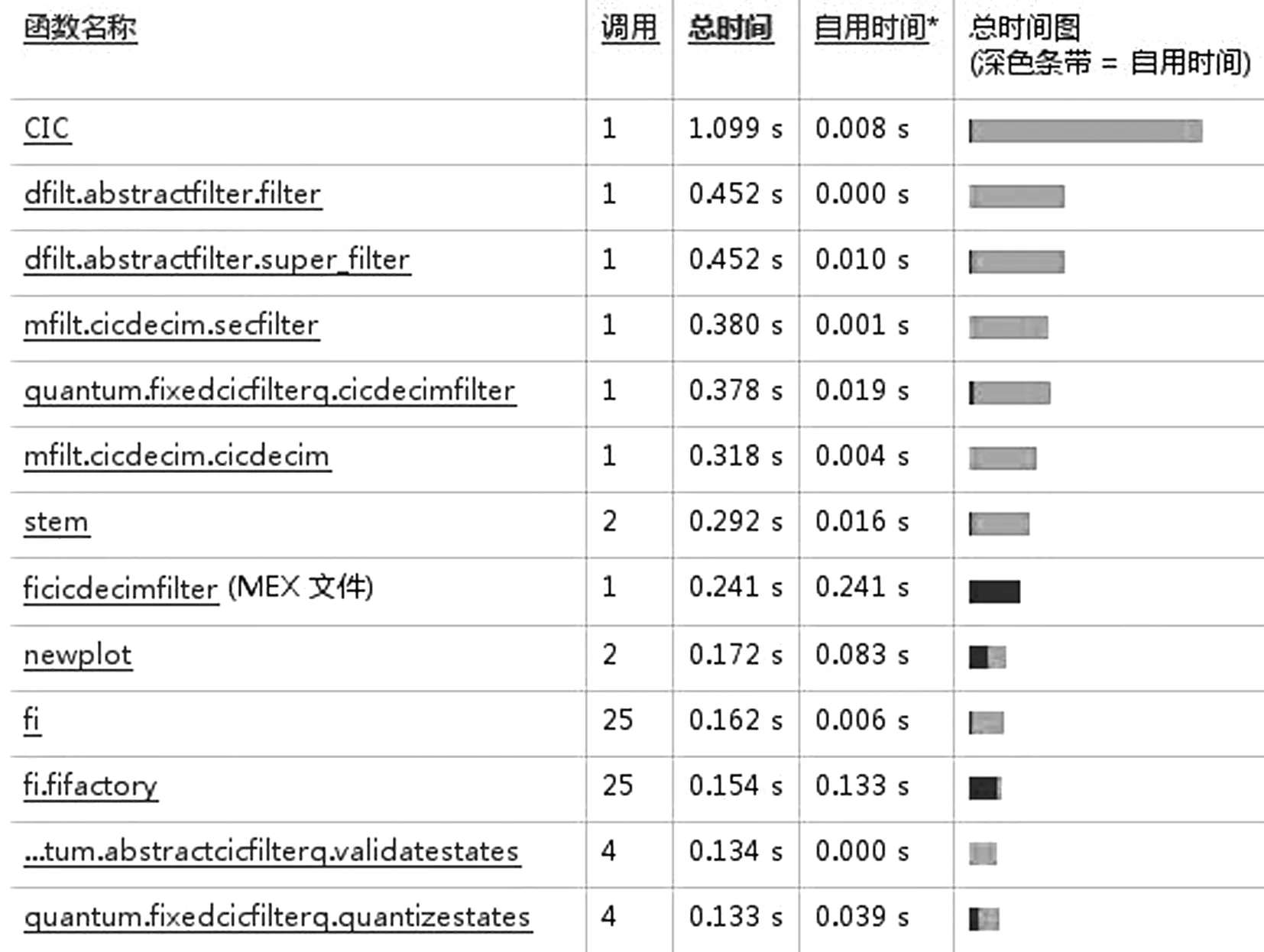
(b) CIC滤波器计算所用时间图6 CIC两倍抽取滤波器抽取结果与计算效率

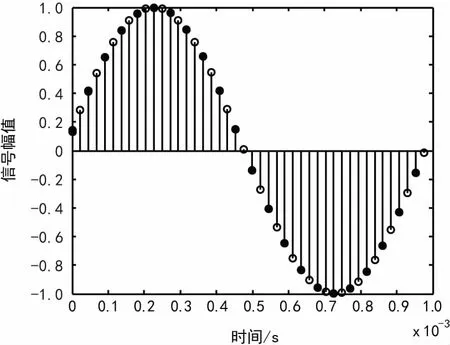
(a) HB两倍抽取时域结果

(b) HB滤波器计算所用时间图7 HB两倍抽取滤波器抽取结果与计算效率

图6(a)和图7(a)显示2种滤波器都能实现2倍的采样率变化，图6(b)与图7(b)分别是2种抽取滤波所用时间，通过对比可以发现HB抽取滤波器总时间为0.590 s，CIC抽取滤波器总时间为1.099 s，HB滤波器比CIC滤波器用时短，计算效率高。所以一般在信号变速率时，首先考虑的是利用HB滤波器。虽然HB滤波器具有上述优点，但是HB滤波器只能完成2N倍采样率变换，实际采样率变换并不一定2N倍，使得在很多环境下无法只利用HB滤波器完成采样率变换，通常会与CIC滤波器相结合，抽取滤波器系统就可以完成任意整数倍的高效抽取频率变换。

2.4 分数倍采样率转换多相滤波器

为实现信号的分数倍采样率转换，可先对输入信号进行整数I倍内插，再进行整数因子D倍抽取来实现[19]。为避免产生不必要的计算量，通常采用的采样结构如图8所示，将下采样过程省略，只需要控制多相内插后的输出转向开关的位置即可。如果旋转开关旋转时，每隔D-1个端口切换一次，就能够得到I/D的采样率变换[20]。

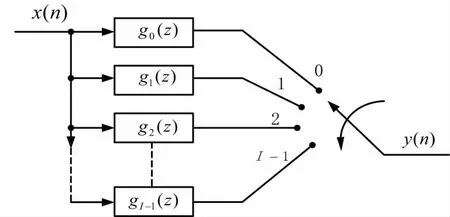
图8 分数倍多相滤波器结构

3 多速率信号处理系统的Matlab仿真

根据多速率信号处理系统中各个滤波器特性以及设计要点的分析，对图2所示系统进行仿真实现。假设输入SINC信号，采样频率fs=4 kHz，选择DCIC=5，DHB=4，多相滤波器I=3,D=5，从抽取倍数看即D多相=5/3，每个环节采样率变化如图9所示，最终输出信号的采样频率为:

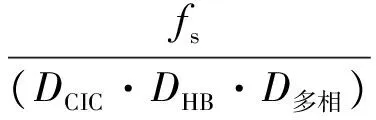
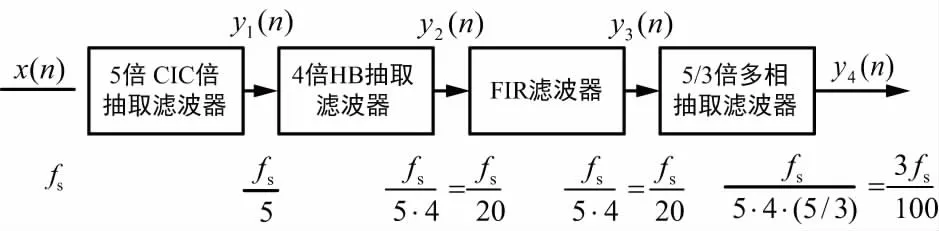
图9 多速率信号处理系统各环节采样率变化

在Matlab环境下，对整个多速率信号处理系统各环节频域进行了仿真，仿真结果如图10～图13所示。

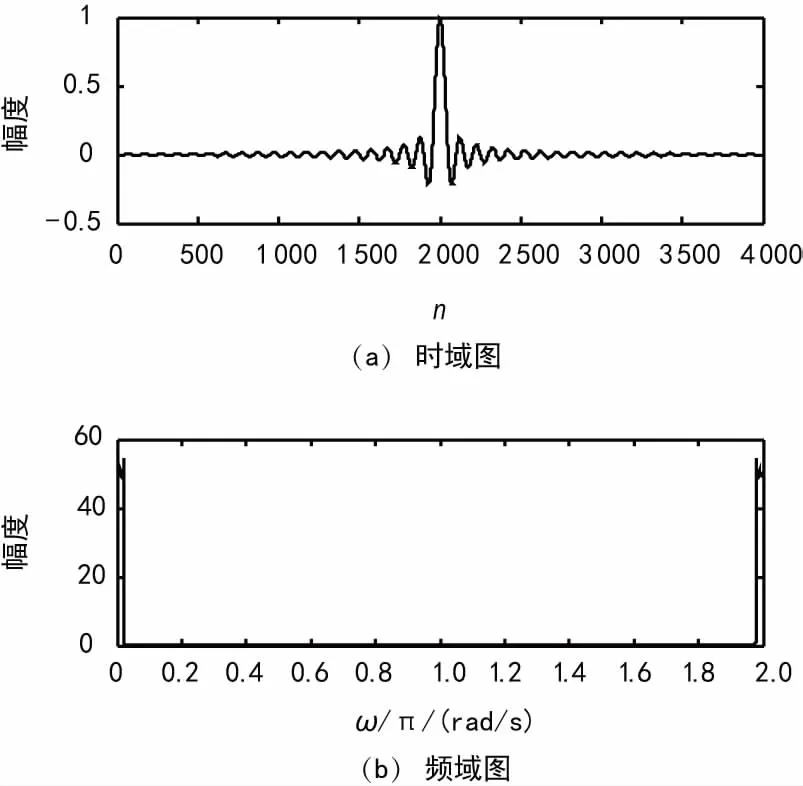
图10 输入信号的时域、频域图

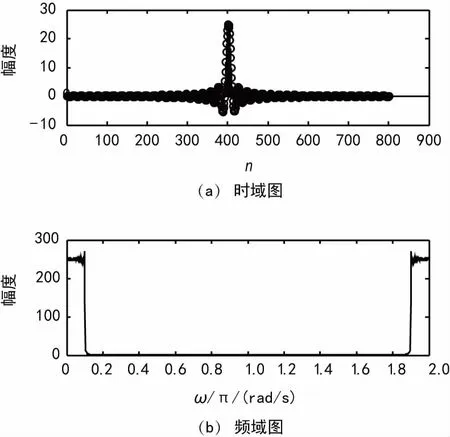
图11 经过CIC后信号的时域、频域图

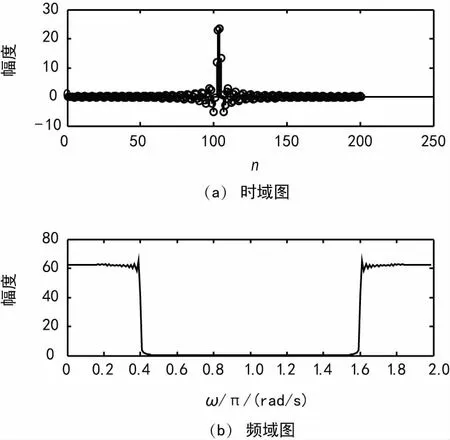
图12 经过HB后信号的时域、频域图

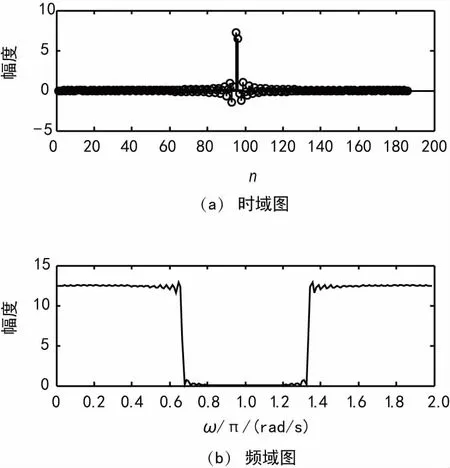
图13 经过多相滤波器后的时域、频域图

由仿真结果可知，抽取使得信号的时域缩短，从而导致频域的展宽，理论上说信号进行了N倍抽取之后，信号的频谱也会对应地展宽N倍。信号通过5倍CIC滤波器抽取后产生信号y1(n)，其幅频特性的频域相比输入信号展宽了5倍，同理有了不同采样率的输出信号y2(n)，FIR滤波器只是对信号进行整形，没有对信号进行抽取，因此y3(n)采样率和y2(n)一样，经过多相滤波器后得到采样率为3fs/100的信号y4(n)。

4 结束语

针对认知无线电中下变频处理中的信号抽取过程对信号频谱的影响进行了研究，对各抽取滤波器的设计及参数选择进行了分析。实验仿真结果表明，CIC滤波器、HB滤波器及多相滤波器都能实现采样率的变换，但每种滤波器有各自的特点，CIC滤波器的长度会影响频谱的主瓣宽度，级数会影响阻带衰减，HB滤波器计算效率高，但只能完成2N倍采样率变换，实际应用时通常会与CIC滤波器相结合，多相滤波器可以高效实现分数倍采样率转换。采样率为fs的信号经过3级抽取，且抽取倍数为DCIC·DHB·D多相时，输出信号的采样率变为fs/(DCIC·DHB·D多相)，因此，这种多级抽取系统能够实现认知无线电中信号的下变频技术，完成信号的多速率转换。

[1] 杨小牛,楼才义,徐建良.软件无线电原理与应用[M].北京:电子工业出版社,2001:57-63.

[2] TUTTLBEE W.软件无线电技术与实现[M].杨小牛,邹少丞,楼才义,等译.北京:电子工业出版社,2005.

[3] 李静,彭华,葛林东,等.用于软件无线电中的整数倍采样率转换技术[J].无线电通信技术,2000,26(3):28-29.

[4] 彭华,李静,葛临东.软件无线电中的非整数倍采样率转换研究[J].电讯技术,2000,40(3):18-23.

[5] 蔡光君,任菊.多速率信号处理技术的实现研究[J].科技创新与生产力,2009(4):65-66.

[6] 陈亦欧,李广军.多速率信号处理的设计与实现[J].实验科学与技术,2006(6):113-116.

[7] 韩治国,王红梅,许辉，等.基于窗函数和特征滤波器的半带滤波器设计[J].计算机仿真,2013(8):181-184.

[8] HARRIS F J.通信系统中的多采样率信号处理[M].王霞,张国梅,刘树棠，译.西安:西安交通大学出版社,2008.

[9] 韩韬.软件无线电数字下变频的研究及系统仿真[D].长春：吉林大学,2006：21-23.

[10] 张茂磊.无线信号多速率接收处理器的设计[D].哈尔滨：哈尔滨工程大学,2011：13-15.

[11] MITOLA.The Software Radio Architecture[J].IEEE Communications Magazine,1995,33(5):26-38.

[12] 栗欣,徐希斌.软件无线电原理与技术[M].北京:人民邮电出版社,2010.

[13] 理查德.数字信号处理与应用[M].北京:机械工业出版社,2015.

[14] DOLECEK G J，CARMONA J D.A New Cascaded Modified CIC-Cosine Decimation Filter[J].IEEE Circuits and Systems,2005(4):218-333.

[15] DOLECEK G J，MITRA S K.On Design of CIC Decimation Filer with Improved Response[J].IEEE International Symposium on Communications,Control and Signal Processing,2008:1072-1076.

[16] 刘益成,林其伟.半带滤波器原理与设计:一种抽取因子为2的FIR滤波器[J].石油管材与仪器,1995,9(1):36-40.

[17] 韩治国,王红梅,许辉.基于窗函数和特征滤波器的半带滤波器设计[J],计算机仿真,2013,30(8):181-184.

[18] RAMSTED T A.Digital Methods for Conversion between Arbitrary Sampling Frequencies[J].IEEE Trans.On Acoust.Speech and Signal Processing,1984,ASSP-232:577-591.

[19] 苟晓刚,周红彬.一种新的多相滤波器结构在FPGA中的实现[J].无线电通信技术,2004,3(4):53-54.

[20] 张志勇.基于多相滤波器原理的多通道软件无线电跳频收发信机的设计与实现[D].北京：北京邮电大学,2013.

TheSpectrumStudyofDigitalDownConversioninCognitiveRadio

LIANG Shuang1,WU Xiao-qin2

(1.CollegeofTelecommunicationsEngineering,XidianUniversity,Xi’anShaanxi710071,China; 2.CollegeofInformationTechnology,HainanUniversity,HaikouHainan570028,China)

The impact of signal decimation on the signal spectrum during the digital down conversion in cognitive radio is studied.The digital signal decimation is composed of cascaded integrator comb (CIC) filter,half-band (HB) filter and poly-phase filer.In order to get the rule of the signal spectrum and know the matters of the parameter selection,the paper gives the theoretical derivation of the signal spectrum in each step by use of the Fourier transform.The test of the whole decimation system is carried by simulation.Both theoretical analysis and simulation results show that the three-stage cascaded decimation system can make the sampling ratefsof the input signal fall tofs/(DCIC·DHBD多相),which is consistent with the theoretical derivation,and the multi-rate conversion can be achieved.

cognitive radio;CIC filter;HB filter;poly-phase filter;spectrum analysis

10.3969/j.issn.1003-3106.2017.12.04

梁爽，伍小芹.认知无线电中下变频信号处理的频谱研究[J].无线电工程,2017,47(12):15-19.[LIANG Shuang,WU Xiaoqin.The Spectrum Study of Digital Down Conversion in Cognitive Radio[J].Radio Engineering,2017,47(12):15-19.]

TN914.3； TN911.72

A

1003-3106(2017)12-0015-05

2017-06-25

国家自然科学基金资助项目(61561017)；海南省自然科学基金资助项目(20166214)。

梁爽女，(1995—)，硕士研究生。主要研究方向：无线通信。

伍小芹女，(1975—)，博士，副教授。主要研究方向：无线通信、数字信号处理。