风向对航母甲板风影响的大涡模拟

袁书生，赵元立，丁伟锋

(海军航空工程学院，山东 烟台 264001)

风向对航母甲板风影响的大涡模拟

袁书生，赵元立，丁伟锋

(海军航空工程学院，山东 烟台 264001)

采用低速气流运动控制方程组和湍流大涡模拟方法，研究了来风风向对航母甲板风的影响，得到了不同来风风向条件下，艏艉对称面附近、甲板上方低场及航母后方某点处压力和垂向速度随时间的变化关系。结果表明：航母有一定角度的侧向风对舰载机起飞有利，右舷风比左舷风有利；从有利于舰载机着舰角度看，右舷来风较左舷来风有利；从舰载机着舰下滑稳定性上看，来风风向角度越小越有利。

航空母舰；甲板风；大涡模拟；舰载机；来风风向

Abstract: The control equations of air flow with lower velocity and the large eddy simulation method of turbulent flows are used to study the effect of the wind direction on the wind over the deck of aircraft carrier. The variety process of pressure and vertical velocity of air motion with time are conducted at some positions over the deck and in the air-wake of aircraft carrier for different directions of wind. When the coming wind has some wind angle, it is propitious to the take off of airplanes from the aircraft carrier, and the effect of right side coming wind is better than that of the left side. On the point of view to facilitate the landing of airplanes, the effect of the right side coming wind is better than that of the left side too. The smaller is the angle of coming winds and the better is the stability for airplanes during descending to aircraft carriers.

Keywords: aircraft carrier；wind over deck；large eddy simulation；shipboard aircraft；head-on wind direction

舰载飞机与陆基飞机的最大区别在于其起降的场域是运动的航母甲板，即使是现代大型航母，其甲板也仅约340 m长、76 m宽[1]。飞行甲板不大，加上航母的运动，及大气绕流航母诱导出的甲板风和尾流，不仅增大了舰载机精确保持下滑轨迹的难度，而且会引起较大的着舰偏差，严重时甚至导致着舰失败[2-3]。

舰载飞机的进舰着舰时，航母尾流和甲板风是精确保持航迹十分重要的影响因素[4-5]。国内外对航母甲板风和尾流效应开展了一些研究，彭兢等人[6]利用工程湍流模型，研究了舰载飞机进舰着舰过程中航空母舰尾流的影响；贲亮亮等人[7]利用雷诺平均湍流模型，研究了不同风速和风向角条件下，舰载飞机进舰轨迹上的流场特性；Polsky[8]利用雷诺平均湍流模型，研究了非稳态甲板风和航母尾流特性；Rajagopalan等人[9]采用模型航母进行了风洞试验，并采用层流假设对试验对象进行了数值模拟；Ryan等人[10]利用雷诺平均湍流模型，模拟了已有的模型航母风洞试验对象，检验了数值模拟的精度。这些成果对舰载机安全起飞与着舰具有重要的参考意义。不过，模拟采用了雷诺平均方法或层流假设，试验则采用了小尺寸模型，所得信息量和结果精度仍不能满足实际需要，雷诺平均模拟是将所有尺度的物理量进行时间平均，并对时间平均的物理量建立守恒方程，脉动量对时均量的影响则采用模型模拟，在相同网格和算法下，其计算精度低于大涡模拟[11]，因为大涡模拟对流动控制方程采用滤波处理，对大尺度的物理量进行直接计算，而仅对小尺度的物理量进行模型模拟[12]；模型风洞试验存在着两个致命的弱点[13]：一是航母模型需要缩小100倍以上，满足相似雷诺数的流动条件难以建立；二是全尺寸舰船的风扰动频率远大于缩比模型，不能真实地反映航母甲板风的瞬间特性。

由于航母体型巨大，加上在海上实际测量不便，数值模拟将成为研究的主要手段。湍流大涡模拟方法相对于雷诺平均模拟方法，具有信息量多、精度较高的优点。本文应用低马赫数气流运动控制方程组和大涡模拟方法，对不同来风风向引起航母甲板风和尾流的变化进行了数值模拟，研究了甲板上方低场和尾流内流动行为具有的特殊性。在低马赫流动假设下，将流体压强和速度解耦[14]，大大地降低了计算工作量，国外已经较多地用于风工程研究中[15-17]；同时本文大涡模拟采用了Deardorff亚格子动力学模型[18]，计算精度是目前多用的亚格子模型中较高的，计算量适中。

1 大涡模拟控制方程组

大气绕流航母是一个典型的冷态、低速空气流动问题。对描述无化学反应、无辐射、浮力作用的气体低速流动过程的湍流瞬时控制方程组，应用盒式滤波器作Favre滤波运算，可得到大涡模拟的控制方程组为：

由于气流速度较低，可采用低马赫数假设[14]，将气流压强分解为背景压强和速度诱导压强之和：

考虑大气分层，大气温度随高度变化为：

式中：Ta为海面处大气温度，Γ为大气温度变化率。

大气密度随高度变化为：

大气背景压强随高度变化为：

计算时不直接求解方程(2)和方程(3)，变化为：

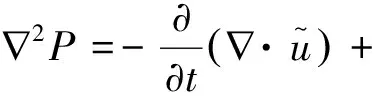
在交错网格系上将上述大涡模拟控制方程组离散，时间上采用显式的二阶精度的预测-校正格式，空间上采用二阶精度的差分格式，对流项则采用基于Superbee通量限制器的TVD格式[21]，扩散项则采用中心差分格式。对压力Poisson方程(11)采用FFT方法直接求解[22]。

2 模拟对象与工况参数

选取图l所示的计算域，长600.0 m、宽300.0 m、高100.0 m。航母模型位于计算域垂直对称面(y=0)上，甲板前沿距离计算域入口80.0 m。航母模型选取与美国“企业”号近似的外形，甲板长333.0 m、宽78.0 m，距离水面20.0 m，舰岛采用长宽高分别为20.0、12.0和20.0 m立方体代替，其几何中心距离甲板前沿200.0 m。

计算中不考虑海浪的影响，假设海面为水平的固体壁面。在计算域入口(x=0 m、y=±150 m)，给定风速条件，出口采用自由边界条件，上表面采用滑移边界条件。在计算域的开口表面上，如果法向速度分量指向域外，则各变量取为自由边界条件，反之各变量则取为外界环境空气的参数。为模拟进口处的扰动，对速度边界条件加上随机噪声[23]，并取随机噪声为均匀分布。

在各坐标方向上分别采用均匀网格划分，网格结点数目取为600×300×100。计算时间取为100.0 s，时间步长由CFL数确定。

本文计算采用大涡模拟软件FDS6.0[24-25]，计算中不考虑舰体与空气之间的热交换。取海面处大气温度为20C，Γ为-0.005 K/m。

为了研究不同风向对航母甲板风和尾流影响的特点，计算时保持来风速度20 m/s，只改变风向。计算工况分为4个，各工况参数如表1所示。

图1 计算区域与航母模型示意Fig. 1 Sketch map of the calculated zone and model carrier

工况12345风向/(°)30150-15-30

注：风矢量与航母艏艉线的夹角定义为正号为风从左舷向后斜向指向右舷，负号为从右舷向后斜向指向左舷。

3 结果分析与讨论

计算选取初始条件为正向来风，速度为10 m/s，压力为环境大气压，只给出了t=40～100 s时均稳定期间的计算结果。

为了分析风向对航母舰载机起飞与降落的影响，本文选取了航母甲板起飞跑道起点、终点和舰尾进场点，研究风向对这些位置低场风的影响，这些位置处具有航母甲板风的典型特征[2]。图2为航母甲板中心线上距离舰首5 m、高度2.5 m位置处的压力与垂向速度随时间的变化。由图2(a)看出，风向对该位置的压力有着较大的影响。风向为±15°时，甲板中心线上距离舰首5 m、高度2.5 m处的压力为正，尽管航母甲板几何不对称，但是该点处的压力差别不大，风向为-15°时略大于风向为+15°时的；而风向为0°和±30°时，该点处的压力均为负，而且风向为0°时压力最低，风向为+30°时的压力比风向为-30°时的要高一点。这一结果说明，由于航母为细长体，且不完全对称，±15°的来风空气扰流航母时，在甲板前端上方产生了有利于起飞的正压力；而来风风向为±30°时，尽管甲板前方的压力仍为负值，但是比正向来风时有所提高。由图2(b)看出，计算的5个来风风向在该位置产生的垂向速度均为有利于起飞的正向速度，不过不同风向来风产生的效果有较大差异。计算结果表明，风向为±15°和±30°时，该点处的垂向速度均大于正面来风时，而且负向来风的垂向速度均大于正向来风的，风向绝对值越大，垂向速度也越大。结合图2的结果分析, 从舰载机起飞角度看, 航母有一定角度的侧向风有利, 风向为负向好于风向为正, 即右舷风比左舷风对起飞有利。比较本文计算的5个工况, 负15°的来风对起飞较为有利。

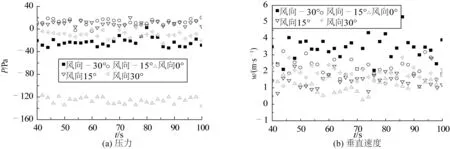
图2 t=40～100 s时航母甲板中心线上距离舰首5 m、高度2.5 m位置处的压力与垂向速度随时间变化模拟结果Fig. 2 The simulated pressure and vertical velocity varieties with respect to time at the point on the bow-stern line of deck 5 m from the bow and 2.5 m over the deck during the time t=40～100 s

图3给出了航母甲板中心线上距离舰首100 m、高度2.5 m位置处的压力与垂向速度随时间的变化。由图3(a)看出, 风向对该位置的压力有一定影响。风向为-30°、-15°和+15°时, 该点处的压力均为正, 并且波动不大；风向为0°, 该点处的压力为负, 波动也不大；但是当来风为+30°时, 平均压力接近零, 可是最大波动达到了250 Pa。显然, 在来风风向为+30°时, 对舰载机的降落存在不利影响。由图3(b)看出, 计算的5个来风风向中, 平均垂向速度均接近0, 但是当来风为+30°时, 垂向速度波动非常明显, 波动的最大值达到了20 m/s, 而当来风为0°、±15°和-30°时, 该位置产生的垂向速度波动非常小。此位置靠近舰载机降落跑道终点, 从有利于舰载机降落角度看, 负向来风较正向来风有利。

图3 t=40～100 s时航母甲板中心线上距离舰首100 m、高度2.5 m位置处的压力与垂向速度随时间变化模拟结果Fig. 3 The simulated pressure and vertical velocity varieties with respect to time at the point on the bow-stern line of deck 100 m from the bow and 2.5 m over the deck during the time t=40～100 s

图4给出了航母甲板中心线上距离舰尾后70 m、海面高度70 m位置处的压力与垂向速度随时间的变化。由图4(a)看出, 风向对该位置的压力也有一定的影响。在所计算的5个工况中, 风向为0°时, 该点的压力最低, ±15°和±30°时, 该点处的压力有所提高, 风向绝对值越大, 压力提高越多, 尽管航母不完全对称, 该点处的压力受风向正负号影响不大。从压力波动值上看, 计算的5个工况中, 风向为±15°时, 波动最明显。由图4(b)看出, 在所计算的5个工况中, 风向对该点的垂向速度平均值影响不大, 但对其波动具有不同的影响。风向为0°和±30°时, 该点处的垂向速度波动较小；风向为±15°时, 该点处的垂向速度波动较大。从舰载机下滑稳定性上看, 来风风向角度越小越有利。

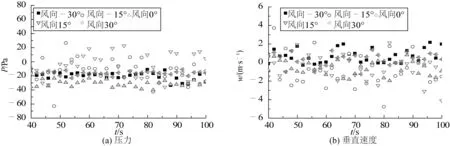
图4 t=40～100 s时航母甲板中心线上距离舰尾后70 m、海面高度70 m空间位置处的压力与垂向速度随时间变化模拟结果Fig. 4 The simulated pressure and vertical velocity varieties with respect to time at the point on the bow-stern line of deck 70 m after the stern and 70 m above sea level during the time t=40～100 s

4 结 语

采用低速气体流动控制方程组和湍流大涡模拟方法, 保持风速不变, 对不同迎面来风风向下的航母甲板风和风尾流行为进行了数值模拟研究, 得到如下结论：

1) 不同迎面来风时, 舰载机起飞离舰点附近的压强差异不大；侧向来风时该区域的垂向速度均大于正向来风, 且右舷来风时的垂向速度高于左舷来风；航母有一定角度的侧向风对舰载机起飞有利, 右舷风比左舷风有利。

2) 迎面来风风向对舰载机着舰点附近区域的垂向速度平均值影响不大, 但是左舷来风时垂向速度的波动幅度较大；右舷来风时该区域的压强明显高于左舷来风；从有利于舰载机着舰角度看, 右舷来风较左舷来风有利。

3) 在0°至左右15°风向之间, 风向角度越小, 风尾流内压强和垂向速度的波动幅度越小；从舰载机下滑稳定性上看, 来风风向角度越小越有利。

[1] 邵开文, 马运义. 舰船技术与设计概论[M]. 北京：国防工业出版社, 2009: 498-497. (SHAO Kaiwen, MA Yunyi. The conspectus about design and technology of ship[M]. Beijing：National Defence Industry Press, 2009: 498-497. (in Chinese))

[2] POLSKY S, NAYLOR S. CVN airwake modeling and integration: initial steps in the creation and implementation of a virtual burble for F-18 carrier landing simulations[C]//AIAA Modeling and Simulation Technologies Conference and Exhibit. 2005: AIAA 2005-6298.

[3] 石明, 屈香菊, 王萌辉. 甲板运动对舰载机人工着舰的影响和补偿[J]. 飞行力学, 2006, 24(1)：5-8. (SHI Ming, QU Xiangju, WANG Menghui. The influence and compensation of deck motion in carrier landing approach[J]. Flight Dynamics, 2006, 24(1)：5-8. (in Chinese))

[4] 许东松, 刘星宇, 王立新. 变化风场对舰载飞机着舰安全性影响[J]. 北京航空航天大学学报, 2010, 36(1)：77-81. (XU Dongsong, LIU Xingyu, WANG Lixin. Influence of changeful wind on landing safety of carrier-based airplane[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(1)：77-81.(in Chinese))

[5] 许东松, 刘星宇, 王立新. 航母运动对舰载飞机着舰安全性的影响[J]. 北京航空航天大学学报, 2011, 37(3)：289-294. (XU Dongsong, LIU Xingyu, WANG Lixin. Influence of carrier motion on landing safety for carrier-based airplanes[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(3)：289-294.(in Chinese))

[6] 彭兢, 金长江. 航空母舰尾流数值仿真研究[J]. 北京航空航天大学学报, 2000, 26(3)：340-343. (PENG Jing, JIN Changjiang. Research on the numerical simulation of aircraft carrier air wake[J]. Journal of Beijing University of Aeronautics and Astronautics, 2000, 26(3)：340-343.(in Chinese))

[7] 贲亮亮, 魏小辉, 刘成龙, 等. 航母甲板风对舰载机进舰轨迹流场影响分析[J]. 舰船科学技术, 2014, 36(1)：27-30. (BEN Liangliang, WEI Xiaohui, LIU Chenglong, et al. Effects of air flow on the landing track of the carrier aircraft[J]. Ship Science and Technology, 2014, 36(1)：27-30.(in Chinese))

[8] POLSKY S A. A computational study of unsteady ship airwake[C]//Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit. 2002: AIAA 2002-1022.

[9] RAJAGOPALAN G, SCHALLER D, WADCOCK A J, et al. Experimental and computational simulation of a model ship in a wind tunnel[C]//Proceedings of the 43th AIAA Aerospace Sciences Meeting & Exhibit. 2005: AIAA 2005-1347.

[10] CZERWIEC R M, POLSKY S A. LHA airwake wind tunnel and cfd comparison with and without bow flap[C]//Proceedings of the 22nd Applied Aerodynamics Conference and Exhibit. 2004: AIAA 2004-4832.

[11] 张兆顺, 崔桂香, 许春晓. 湍流理论与模拟[M]. 北京：清华大学出版社, 2006: 260-262. (ZHANG Zhaoshun, CHUI Guixiang, XU Chunxiao. Theory and modeling of turbulence[M]. Beijing：Tsinghua University Press, 2006: 260-262. (in Chinese))

[12] 张兆顺, 崔桂香, 许春晓. 湍流大涡数值模拟的理论和应用[M]. 北京：清华大学出版社, 2008: 57-58. (ZHANG Zhaoshun, CHUI Guixiang, XU Chunxiao. Theory and modeling of turbulence[M]. Beijing：Tsinghua University Press, 2008: 57-58. (in Chinese))

[13] POLSKY S A. A computational study of unsteady ship airwake[C]//Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit. 2002: AIAA 2002-1022.

[14] REHM R G, BAUM H R. The equations of motion for thermally driven, buoyant flows[J]. Journal of Research of the NBS, 1978, 83：297-308.

[15] REHM R, MCGRATTAN K, BAUM H, et al. An efficient large eddy simulation algorithm for computational wind engineering: application to surface pressure computations on a single building[R]. NISTIR 6371, 1999.

[16] REHM R G, MCGRATTAN K B, BAUM H R. Large eddy simulation of flow over a wooded building complex[J]. Wind & Structures, 2002, 5(2)：291-300.

[17] CHANG C H, MERONEY R N. Concentration and flow distributions in urban street canyons：wind tunnel and computational data[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91：1 141-1 154.

[18] DEARDORFF J W. Numerical investigation of neutral and unstable planetary boundary layers[J]. Journal of Atmospheric Sciences, 1972, 29：91-115.

[19] DEARDORFF J W. Stratocumulus-capped mixed layers derived from a three-dimensional model[J]. Boundary-Layer Meteorol, 1980, 18：495-527.

[20] WERNER H, WENGLE H. Large-eddy simulation of turbulent flow over and around a cube in a plate channel[C]//Proceedings of the 8th Symposium on Turbulent Shear Flows. 1991, 34：155-168.

[21] ROE P L. Characteristics-based schemes for the Euler equations[J]. Ann. Rev. Fluid Mech., 1986, 18：337-340.

[22] SWEET R A. Direct methods for the solution of poission’s equation on a staggered grid[J]. Journal of Computational Physics, 1973, 12：422-428.

[23] BAUM H R, REHM R G, BARNETT P D, et al. Finite difference calculations of buoyant convection in an enclosure, part i: the basic algorithm[J]. SIAM Journal of Scientific and Statistical Computing, 1983, 4(1)：117-135.

[24] FLOYD J, FORNEY G, HOSTIKKA S, et al. Fire dynamics simulator(version 6)-technical reference guide[M]. NIST Special Publication 1018, 2014.

[25] FLOYD J, FORNEY G, HOSTIKKA S, et al. Fire dynamics simulator(version 6)-user`s guide[M]. NIST Special Publication 1019, 2014.

Large eddy simulation to the effect of wind direction on wind over the deck of aircraft carrier

YUAN Shusheng，ZHAO Yuanli，DING Weifeng

(Naval Aeronautical and Astronautical University，Yantai 264001，China)

1005-9865(2017)02-0001-06

V211.3

A

10.16483/j.issn.1005-9865.2017.02.001

2015-12-08

袁书生(1963-)，男，河北武邑人，教授，博士生导师，从事湍流多相流与燃烧研究。E-mail：yuanshusheng@tsinghua.org.cn