基于转子分段斜极的齿槽转矩优化设计

李卫民，刘 阳，陈 静，井天尧

（辽宁工业大学 机械工程与自动化学院，辽宁 锦州 121001）

基于转子分段斜极的齿槽转矩优化设计

李卫民，刘 阳，陈 静，井天尧

（辽宁工业大学 机械工程与自动化学院，辽宁 锦州 121001）

通过理论计算和数值仿真，确定了有槽永磁同步电机的合理设计方案，有效地削弱了齿槽转矩。推导出了分段斜极最佳斜极角度与分段数的关系式，根据实际永磁同步电机设计出实现分段斜极的结构方案，通过Maxwell16对不同分段数进行仿真分析来确定最佳分段斜极的分段数，实现优化设计的目的。

永磁同步电机；齿槽转矩；转子分段斜极

随着永磁电机的广泛应用，对其性能要求也越来越高。在有槽永磁电机中，齿槽转矩的存在，是引起电机振动及噪音的关键因素。在永磁电机的设计过程中通常会采用各种方法来削弱齿槽转矩[1-3]，比如斜槽与斜极、磁极不对称分布、磁极偏移等。王秀和[4]等人以外转子永磁电机做了详细的分析总结，而针对内置式永磁电机的研究较少。文献[5]和[6]通过几何矢量关系的方法推导出了分段斜极的最佳斜极角度，没有进行深入的理论推导计算。本文将以一台内置式永磁同步电机模型为例，通过对齿槽转矩的傅里叶级数展开式推导出分段斜极的最佳斜极角度,并设计出分两段及多段斜极的斜极结构方案,最后结合有限元仿真软件 Maxwell16的仿真结果确定了最佳的分段斜极的分段数，从而实现以最优的设计方案有效地削弱齿槽转矩。

1 基于分段斜极的齿槽转矩理论分析

根据现有的研究成果，在不考虑定子斜槽时的齿槽转矩[4]Tcog可表示为:

式中：p为磁极对数；z为定子槽数；α为某一个特定的定子齿的中心线与特定转子中永磁体中心线夹角；μ0气隙磁导率；Brπz/2p为永磁体产生的气隙磁密平方的傅里叶分解系数；La为转子的轴向长度；R1、R2分别为转子外半径和定子轭内半径；n为满足nz/2p为整数的整数。

齿槽转矩产生的机理是：在永磁电机绕组不通电的情况下，永磁体与定子齿槽间产生相对转动而引起的磁场能量变化所产生的相互作用力的切向分量引起的转矩。采用分段斜极的方法可以有效地削弱齿槽转矩。图1（a）为一般的磁极结构。图1（b）为分段斜极结构，即为把永磁体沿轴向分为尺寸相同的若干段，并在圆周方向排布时依次错开一定的斜极角度。

图1 永磁体磁极结构

设分段数k为定值，相邻两段转子铁芯沿圆周方向的斜极角度为Nsθs1,其中Ns为定子所斜的槽数，θs1为用弧度表示的两个定子齿间的齿距。分段斜极相当于将永磁电机转子的铁心与永磁体同时沿轴向均等分成k段，这k段转子分别产生的齿槽转矩分别为：

永磁电机的总齿槽转矩为这k段转子所产生的齿槽转矩之和，即

2 分段斜极削弱齿槽转矩的方法研究

2.1 电机模型

以下研究内容均是以8极48槽内置式永磁同步电机展开的。根据电机模型的主要参数如表 1，在Maxwell16.0电磁场分析软件中建立电机截面模型如图2所示。

表1 电机模型的主要参数 (mm)

图2 电机截面模型

2.2 最佳斜极角度的确定

采用分段斜极的方法来削弱齿槽转矩时，斜极的角度直接影响着齿槽转矩的削弱效果。理想状态下，当分段斜极的分段数k→∞时，即可理解为连续斜极；而连续斜极对齿槽转矩削弱原理和效果与定子斜槽是相同的；定子斜槽角度为一个齿距θs1时，对齿槽转矩的削弱效果是最佳的[7]。所以在一个齿距范围内存在一个最佳的分段斜极角度，能达到最佳削弱齿槽转矩的效果。

由式（3）可以看出：

(1)当nNs=1，2，3…时，分k段斜极的总齿槽转矩表达式为：

可见齿槽转矩式（4）与不考虑斜槽时的齿槽转矩表达式（1）是完全一样的，这就说明当满足nNs=1，2，3…时，分段斜极对齿槽转矩谐波并没有起到削弱的效果。

(2)当nNs≠1，2，3…时，分k段斜极的总齿槽转矩表达式为：

可知，当nNs≠1，2，3…时，存在条件

即满足

即

上述中，Np表示转子相对于定子旋转一个齿距，齿槽转矩变化的周期数，即为：

其中，F(z，2p)表示槽数z与极数2p的最大公约数。

依据所采用的电机模型参数，Np=1。将式（8）代入到式（2）中可知，当采用分k段斜极时，以第一段转子铁心为基准，第k段转子铁心相对于第一错开的斜极角度θk为：

式（9）是在nNs≠1，2，3…条件下得到的，因此斜极角度θk即为采用分k段斜极时的最佳斜极角度，采用此斜极角度对齿槽转矩的削弱效果是最好的。

2.3 实现分段斜极的结构方案

实现分段斜极的方法有很多种，比如文献[8]中提出的在转子铁心叠片上设置定位孔或键槽，每段转子铁心叠片上定位孔的相对位置不同，通过定位孔来实现斜极。文献[9]也是通过在转子铁心上设置定位键槽来实现分段斜极，以上这些方法行之有效；由于转子铁心叠片的数量很多，在每片叠片上都设置这种定位孔或定位槽时很难控制其位置精度，而且这样的转子铁心叠片也不具有通用性。为此，本文提出了一种新型的分段斜极结构，不仅能够很好地控制分段斜极角度的位置精度，而且此类的转子叠片也可以作为不斜极转子铁心叠片，具有很好地通用性。

以分两段斜极为例如图3、4所示，转子铁芯5和铁芯7上开有永磁体槽1和键槽3；转子转轴8上有两组不对称的左面齿9和右面齿11，转轴中间设有轴肩10。两个转子铁芯通过键槽2与转轴上的左面齿9和右面齿11相配合，在轴肩10上安装有隔磁垫片6。转轴8左齿中心线12与右面齿中心线13形成θ角。当转子的两部分铁芯安装到转轴8上时，转子铁芯5永磁体槽1中心线4与转子铁芯7永磁体槽1中心线3之间也形成了θ角，从而实现转子分段斜极。

图3 分段斜极转子结构示意图

图4 转轴示意图

此结构的优点在于，通过转子转轴上两组相互错开的齿来实现分段斜极的斜极角度，只要准确控制这两组齿错开的角度，就能保证精确的斜极角度；而在转子铁心叠片上只需要在固定的位置加工与转轴相配合的键槽即可。若采用分三段及以上转子斜极，则依然可以采用此方案，此时转子转轴需要采用阶梯轴来实现，实施原理与分两段斜极相同；以分三段为例阶梯轴如图5所示，其他不在赘述。

图5 分三段斜极转轴示意图

2.4 分段斜极后的有限元仿真

分段斜极的分段数越多，对齿槽转矩的削弱效果越明显[9]，但转子铁心生产制造工艺性难度也越高。因此采用分段斜极方案时，要选择合适的分段数来达到优化效果的同时还要保证其具有良好的工艺性。本文利用Maxwell16.0采用2D有限元分段分析法解决3D问题[10-11]，分别进行了分2、3、4段斜极仿真分析。

不分段时的齿槽转矩如图6所示。根据式（9）可知，分两段斜极时的最佳斜极角度为θ2=3.75°，齿槽转矩如图7所示；分三段斜极时的最佳斜极角度为θ3=5°，齿槽转矩如图8所示；分四段斜极时的最佳斜极角度为θ4=5.625°，齿槽转矩如图9所示。

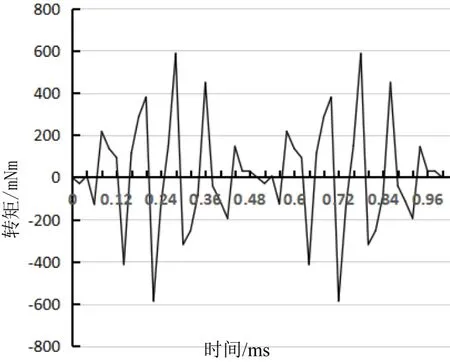
图6 不分段时的齿槽转矩

图7 分两段时的齿槽转矩

图8 分三段时的齿槽转矩

图9 分四段时的齿槽转矩

2.5 仿真结果分析

通过仿真结果可看出，分段斜极后的齿槽转矩相对于不分段时的削弱程度，如表2所示。

表2 齿槽转矩削弱程度对比

从优化结果看出，采用分段斜极可以有效地削弱齿槽转矩效应，当采用分 2段斜极时削弱了67.9%；采用分3段斜极时削弱了88.5%，相对于分2斜极削弱了 20.6%；采用分 4段斜极时削弱了93.8%，相对于分3段斜极削弱了9.5%，削弱幅度较小。实际上对齿槽转矩的要求是越小越好，综合齿槽转矩的削弱效果，并考虑到转子铁心的生产制造工艺性，采用转子分三段斜极为最佳方案。

3 结束语

通过对齿槽转矩傅里叶级数展开式的分析，理论推导了转子最佳斜极角度与分段数的关系式，并设计出了工艺性能较好的分段斜极结构方案，结合有限元仿真，分别对分2、3、4段斜极进行仿真分析，从分析结果对比，结合实际生产工艺性要求，确定分3段斜极为最佳的分段斜极方案。综上所述，采用此分段斜极方案能有效地削弱齿槽转矩，实现优化设计的目的。

[1]HWANG S M,EOM J B,HWANG G B,et al.Cogging torque and acoustic noise reduction in permanent magnet motors by teeth pairing[J].IEEE Transactions on Magnetics,2000,36(5): 3144-3146.

[2]THOMAS M J,WEN L S.Pulsating torque minimization techniques for permanent magnet AC motor dreves: a reciew[J].IEEE Transactions on Industry Electronics,1996,43(2): 321-330.

[3]NICOLA B,SILVERIO B.Design techniques for reducing the cogging torque in surfacee-mounted PM motors[J].IEEE Transactions on Magnetics,2002,38(5): 1259-1265.

[4]王秀和.永磁电机[M].北京: 中国电力出版社,2007.

[5]应红亮,张舟云,曲家骐,等.转子分段斜极在永磁同步电动机中的应用分析[J].微特电机,2009(7): 10-13.

[6]彭俊,符敏利,陈致初,等.永磁同步电机转子分段斜极的分析研究[J].大功率变流技术,2012(1): 50-53.

[7]李华,龚天明,祝令帅.定子斜槽结构对永磁同步电动机影响的分析[J].防爆电机,2012,47(4): 6-10.

[8]蒋卿正,张跃冬.单一冲片构成的分四段斜极永磁电机转子: 中国,201420 277294.8[P].2014-05-28.

[9]彭俊,李益丰,符敏利,等.一种分段斜极的永磁电机转子: 中国,201110330939.0[P].2011-10-27.

[10]黄燕涛,郭新华,项雷军.内置式永磁电机齿槽转矩的优化设计[J].华侨大学学报: 自然科学版,2016,37(5):536-540.

[11] Eastham J F,Ionel D M,Balchin M J,et al.Finite element analysis of an interior-magnet brus-hless DC machine,with a step-skewed roror[J].IEEE Transactions on Magnetics,1997,33(2): 2117-2117.

Optimal Design of Cogging Torque Based on Step Skewing of Rotor

LI Wei-min,LIU Yang,CHEN Jing,JING Tian-yao
（College of Mechanical Engineering & Automation,Liaoning University of Technology,Jinzhou 121001,China）

By theoretical calculation and numerical simulation,the reasonable design scheme of slot permanent magnet synchronous motor is determined,and the cogging torque is effectively weakened.The relationship between the optimum step skewing angle and the number of segments is derived.According to the actual permanent magnet motor,the structure scheme of the step skewing is designed.Through Maxwell16 simulation analysis of the number of different segments is made to determine the best segment number of the step skewing,and the purpose of optimization design is achieved.

permanent magnet synchronous motor(PMSM)；cogging torque；step skewing of rotor

TP391

A

1674-3261(2017)05-0307-05

10.15916/j.issn1674-3261.2017.05.007

2017-07-05

辽宁省科技攻关计划项目资助（2014106008）

李卫民(1965-)，男，辽宁朝阳人，教授，博士。

责任编校：刘亚兵