半主动悬架的自适应滑模控制

王 新，孙丽颖

（辽宁工业大学 电气工程学院，辽宁 锦州 121001）

半主动悬架的自适应滑模控制

王 新，孙丽颖

（辽宁工业大学 电气工程学院，辽宁 锦州 121001）

针对外部干扰及不确定参数对汽车悬架的影响，基于1/4车辆二自由度半主动悬架系统的非线性模型，设计了自适应滑模控制器。该方法采用滑模控制来减小外部干扰对系统的影响，并使用双曲正切函数改善抖振现象。同时采用自适应Backstepping方法跟踪不确定参数。仿真结果表明了该方法所设计控制器的有效性。

车辆；半主动悬架；滑模控制；自适应Backstepping

悬架系统作为汽车的重要组成部分，对车辆行驶的操纵稳定性、平顺性和乘坐舒适性有着重要影响。传统的被动悬架系统无须外部能量输入，结构简单，因而获得广泛应用，但不能适应变化的行驶工况和任意道路激励[1]。主动悬架能获得一个优质的隔振系统，实现理想悬架的控制目标，但能量消耗大、成本高、结构复杂。能量、成本和可靠性是限制主动悬架发展的瓶颈[2]。半主动悬架通过调节减振器阻尼，可适应不同道路和行驶状况，从而提高乘坐舒适性和操纵稳定性。由于半主动悬架结构简单、能耗低，而控制品质接近主动悬架，因此受到了广泛的关注和研究。

文献[3]考虑了液压装置的动力学特性，提出了线性二次型指标下最优控制与反演控制结合的内外环控制策略，但忽略了悬架系统参数的不确定性。文献[4]通过配置极点和利用等效控制设计了滑模切换面函数和滑模控制器，并利用光滑函数消除抖振，也未考虑系统的不确定性及外部干扰。文献[5]考虑了系统中各种参数的不确定性，采用自适应Backstepping方法设计控制器，能自动调节控制器参数，适应系统参数在一定范围内的变化，但设计过程比较复杂。

本文充分考虑半主动悬架系统的非线性特性、参数不确定性以及外加干扰的影响，采用滑模控制与自适应Backstepping方法相结合的控制策略设计控制器，保证了车辆在不同的行驶状况下悬架系统的稳定性，同时改善了乘坐的舒适性和安全性。

1 半主动悬架模型

为方便研究，本文选取1/4车辆二自由度半主动悬架系统作为研究对象，其简化模型如图1所示。

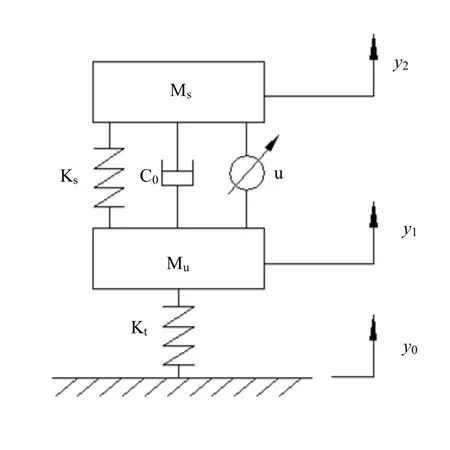
图1 悬架模型

该系统运动学方程可描述为[6]：

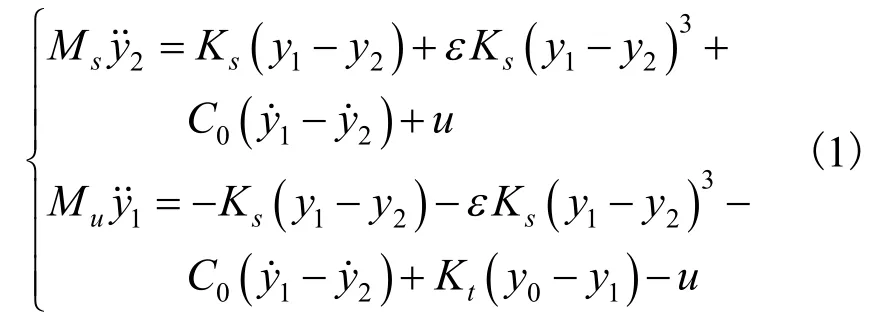
式中：ε＞0代表悬架刚度的非线性程度；Ms和Mu分别为车身质量和轮胎质量；y2和y1分别为车身垂向位移和轮胎垂向位移；y0为路面激励；Ks和C0分别为悬架系统刚度和阻尼系数的不可调部分；Kt为轮胎刚度系数；u为半主动悬架的控制力。

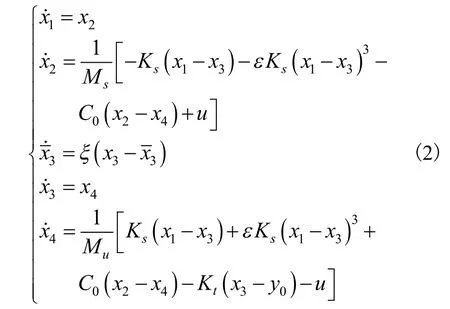
在半主动悬架系统中，车辆的运动状态及工作环境会发生变化，现定义不确定参数θ1=Ks，θ2=C0，同时考虑可能存在的外部扰动，将式(2)改写为：

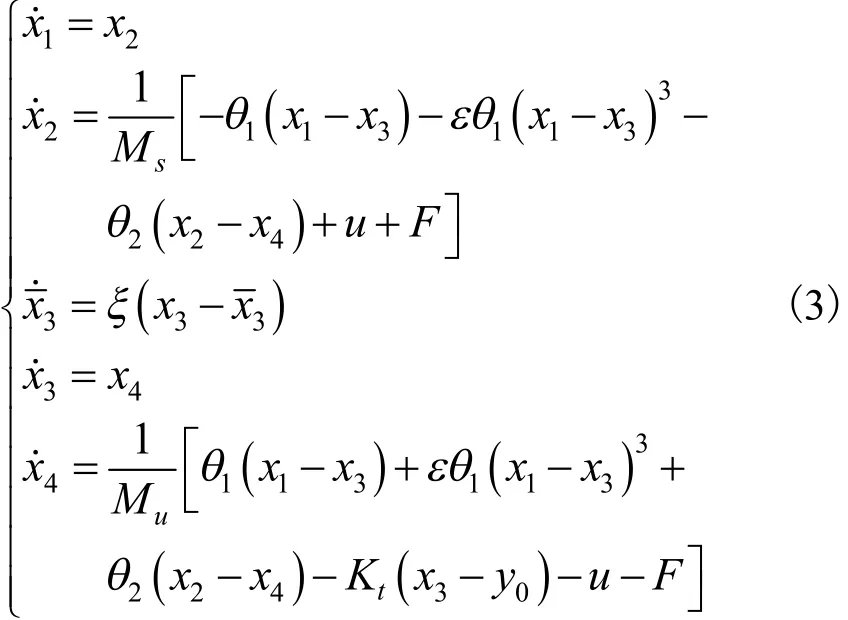
其中F为不确定的外部干扰，且F有界。现假设∣F∣≤D，D＞0为常数，不确定参数θi有界，即i=1,2。下面给出控制器设计过程中需要用到的引理。

引理 1[8]取η＞0，对于任意χ∈R，存在常数η＞0，如下不等式成立：

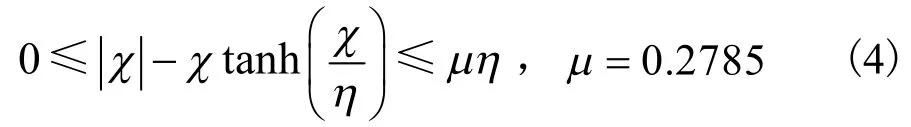
引理2[9]针对V：不等式方程的解为：

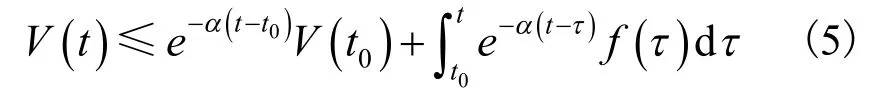
其中，α为任意常数。

2 控制器设计

针对悬架系统中存在的不确定参数及未知扰动，采用自适应Backstepping与滑模控制相结合的方法设计控制器，使得系统对干扰具有鲁棒性。

首先，考虑误差变量：

对式(6)求导得：

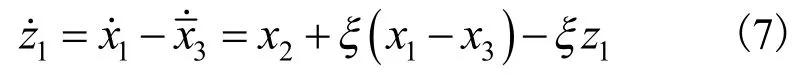
定义第一个Lyapunov函数为：

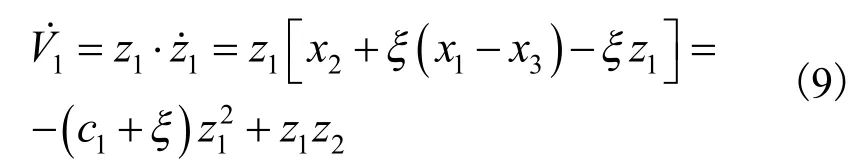
对式(10)求导可得：

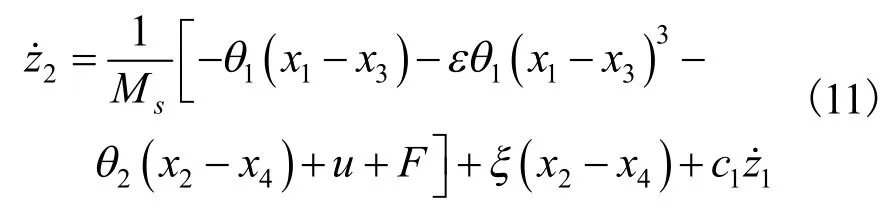
现取控制律为：

其中c2＞0为常数，为iθ的估计值，i=1,2。

定义第二个Lyapunov函数：

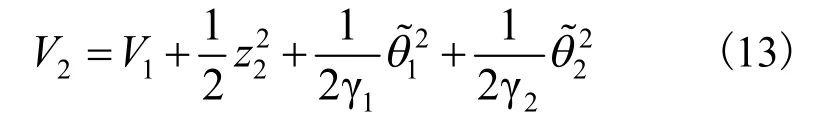
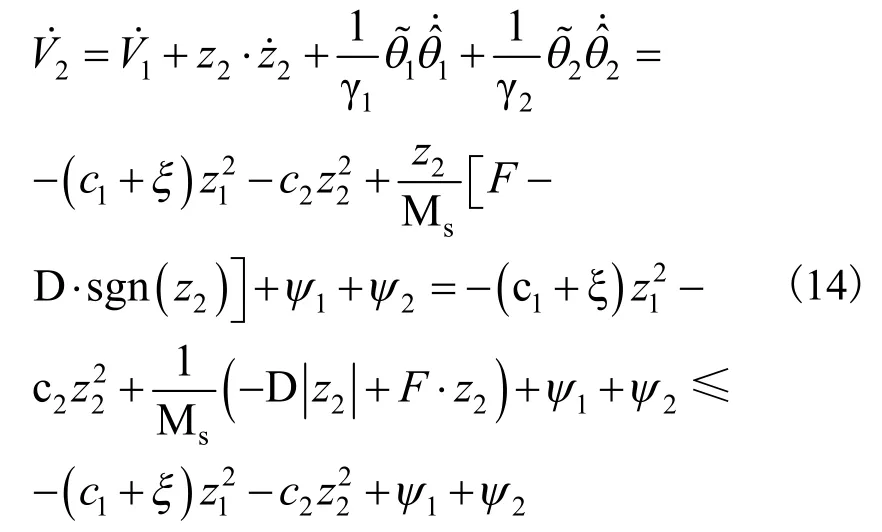
其中：

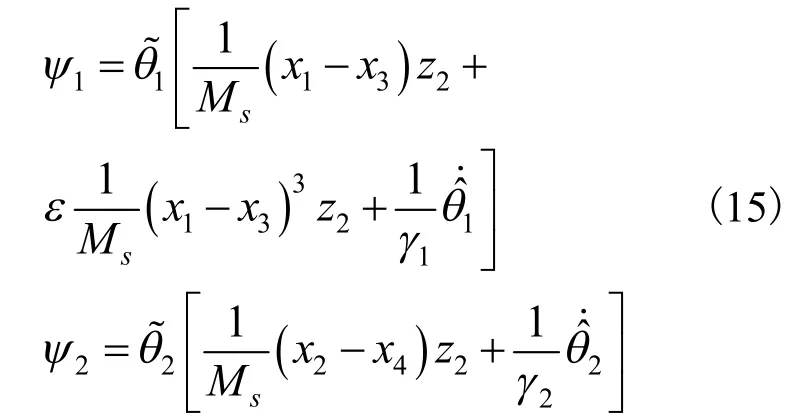
取投影自适应律[10]为：

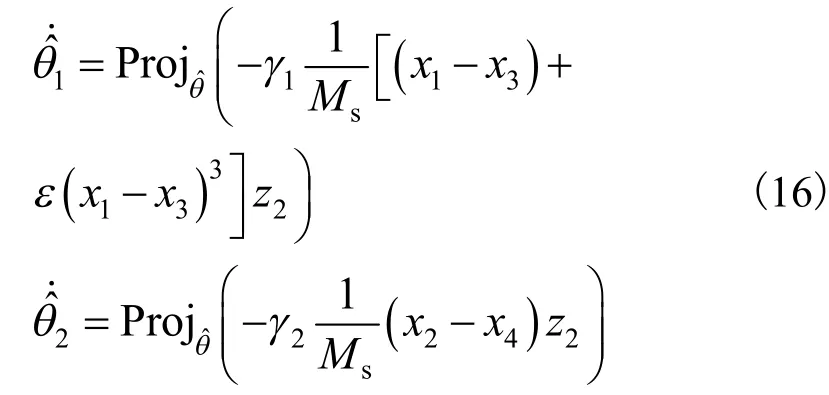
其中：

则有：

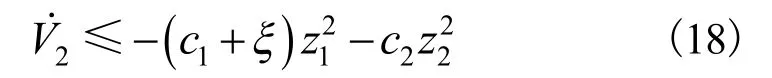
通过选择c1，c2可使得半负定，误差渐进稳定，从而在给定的控制律下系统是渐进稳定的。但是，当系统的外加干扰较大时，切换项增益D也会变得很大，会造成较大的抖振[11]。为了有效降低抖振，在控制器设计中采用双曲正切函数η＞0代替符号函数sgn(z2)，即：

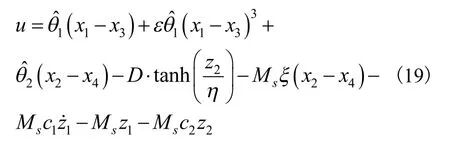
由引理1可知：

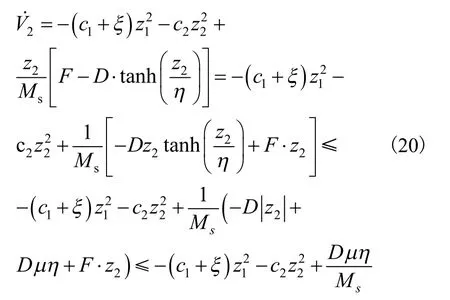
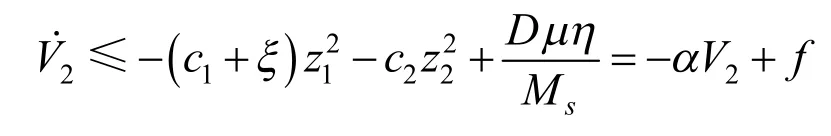
令输出y≡0，得到系统的零动态：

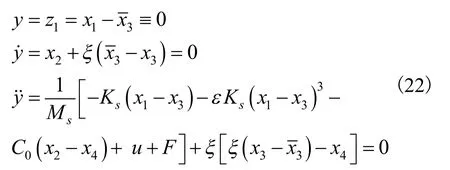
将

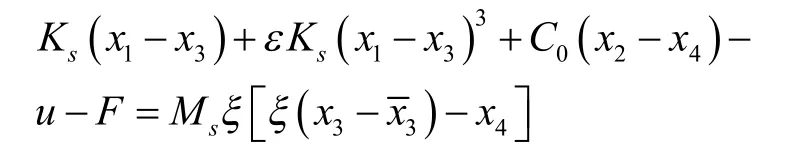
代入零动态可得：

改写为矩阵形式：

当且仅当ξ＞0时，此3阶矩阵是Hurwitz的，零动态渐进稳定。

3 仿真实验

采用 MATLAB进行仿真以检验设计的控制算法

的有效性。仿真中悬架模型的参数[12]为：Ks=13 720 N/m，Kt=1.76×105N/m，C0=282 N⋅ s/m，Ms=215 kg，Mu=36 kg 。控制器及滤波器参数为：ε=0.4，ξ=1，c1=100，c2=0.1，η=0.02。自适应律参数为：γ1=8.4×108，γ2=1.5×107，θ1min=1.3×104，θ1max=1.4×104，θ2min=260，θ2max=300。仿真中考虑两种路面信号，分别为凸起路面信号和正弦信号，而外加扰动信号为一正弦信号。

凸起路面信号：y0=0.04（1-cos8πt） 0.5≤t≤0.75

正弦路面信号：y0=0.06sin6πt

扰动信号：F=80sin8πt1.5≤t≤1.75

路面及扰动信号如图2所示。

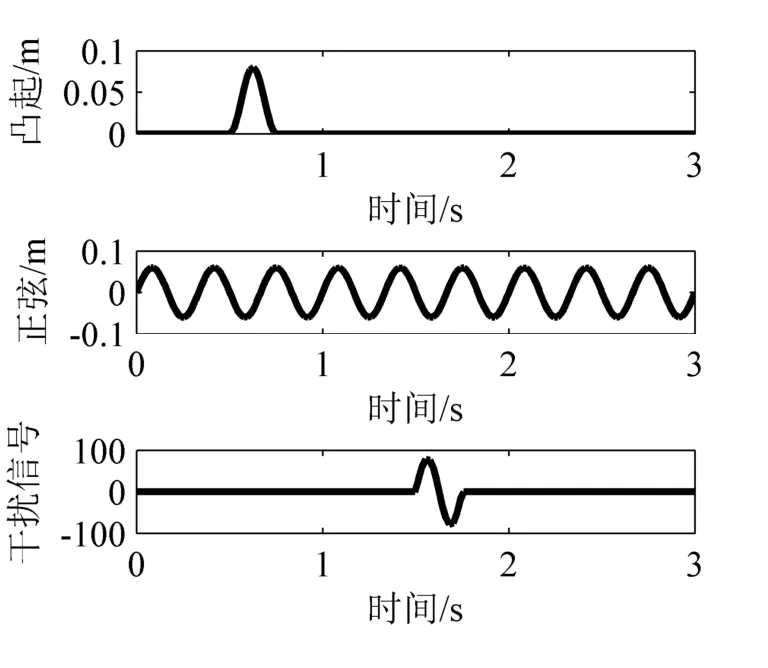
图2 路面及扰动信号

在凸起路面信号作用下，车身垂直加速度、悬架动行程曲线分别如图3、图4所示。控制输入曲线及自适应曲线如图5、图6所示。由仿真结果可以看出，相比于被动悬架，所设计的控制器明显提高了悬架的减振效果，而且有效地降低了外加干扰对系统的影响。同时，采用双曲正切函数代替符号函数，很好地解决了滑模控制中出现的抖振现象。

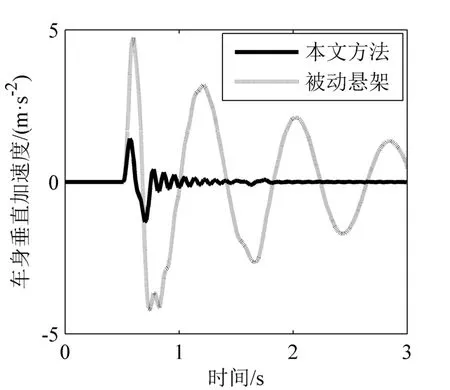
图3 凸起信号下车身垂直加速度曲线

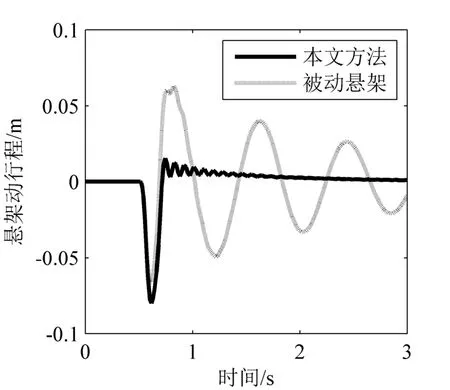
图4 凸起信号下悬架动行程曲线

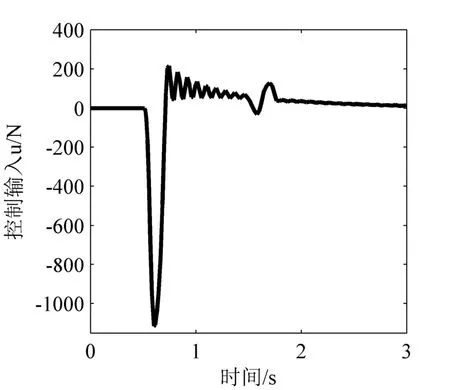
图5 凸起信号下控制输入曲线

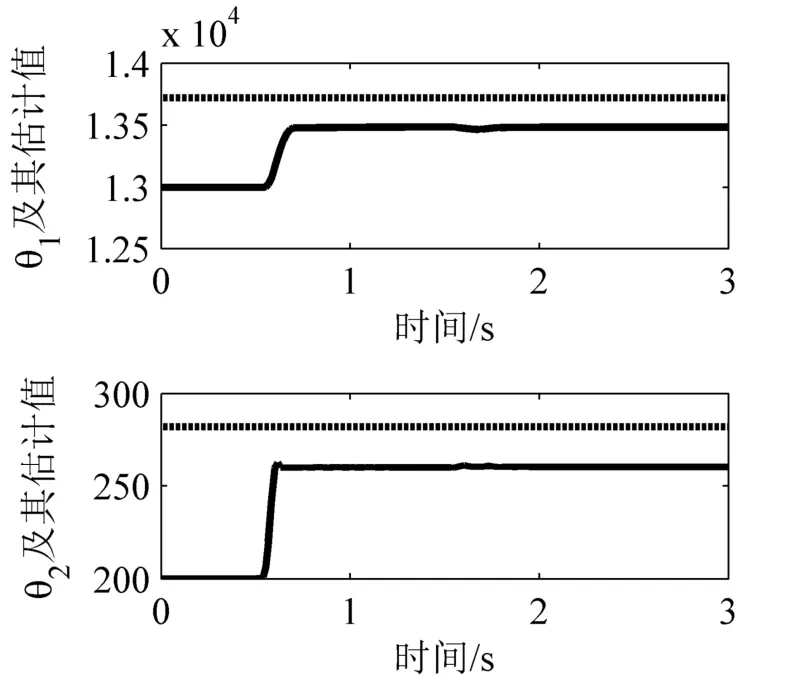
图6 凸起信号下自适应曲线

图7和图8为正弦信号下的车身垂直加速度曲线和悬架动行程曲线。图9为控制输入曲线，图10为自适应参数的变化曲线。比较可以看出，在正弦激励信号下，设计的半主动悬架依然保持良好的性能，当输入干扰信号时，车身加速度没有明显的变化，而自适应参数可以快速恢复到实际值附近。

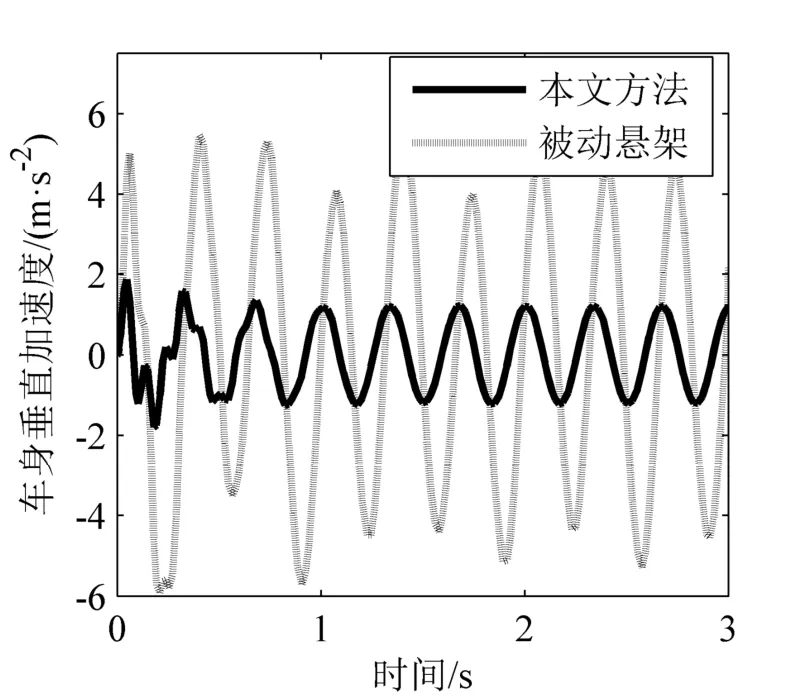
图7 正弦信号下车身垂直加速度曲线

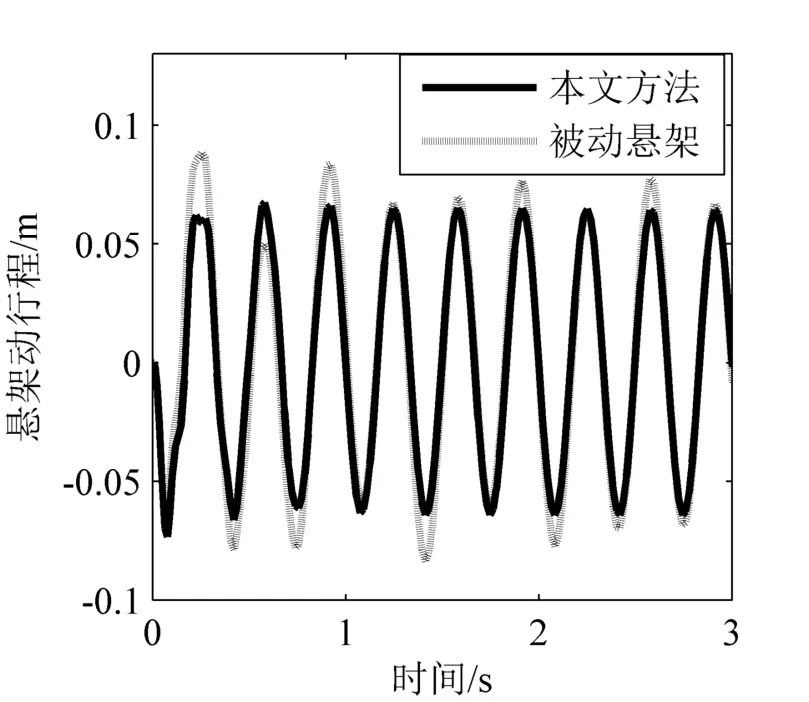
图8 正弦信号下悬架动行程曲线

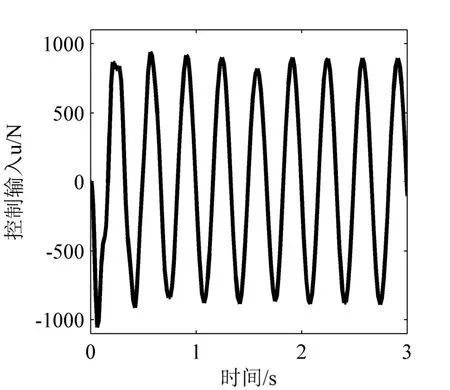
图9 正弦信号下控制输入曲线

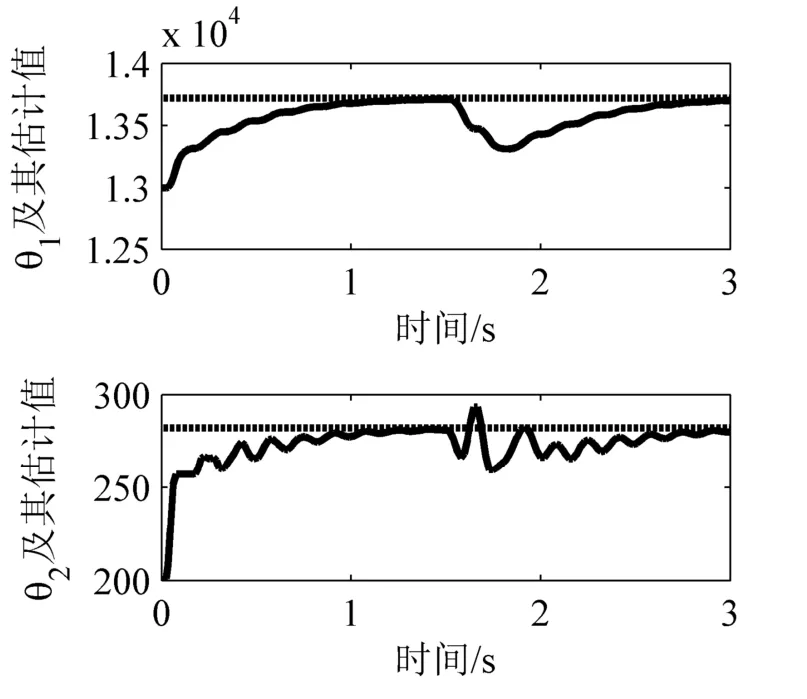
图10 正弦信号下自适应曲线

4 结论

基于半主动悬架系统模型，充分考虑系统的非线性特性以及悬架减振器阻尼力的变化情况，采用自适应Backstepping方法设计控制器，使用滑模控制方法抑制系统中可能存在扰动的问题，并以双曲正切函数代替切换函数消除抖振现象，改善了控制品质。仿真结果表明，设计的控制器保证了半主动悬架系统的稳定性和鲁棒性。

[1]姚嘉伶,蔡伟义,陈宁.汽车半主动悬架系统发展状况[J].汽车工程,2006,28(3): 276-280.

[2]方子帆,邓兆祥,郑玲,等.汽车半主动悬架系统研究进展[J].重庆大学学报,2003,26(1): 104-108.

[3]刘震,吴冰,胡德文.基于 Backstepping方法的液压主动悬挂最优控制及仿真[J].系统仿真学报,2007,19(3):616-619.

[4]郑明军,张晓磊,吴文江.半主动空气悬架的滑模变结构控制[J].机械设计与制造,2015,(1): 87-90.

[5]赵海英,邝钰,吴忠强.汽车主动悬架的自适应Backstepping控制[J].制造业自动化,2013,35(8):113-117.

[6]赵和平,黄宏成,习纲,等.非线性弹簧汽车悬架动态特性研究[J].机械强度,2001,23(2):165-167.

[7]Jung-Shan Lin,Ioannis Kanellakopoulos.Nonlinear Design of Active Suspensions[J].IEEE Control Systems,1997,17(3): 45-59.

[8]Polycarpou M M,Ioannou P A.A robust adaptive nonlinear control design[M].Pergamon Press,lnc.1996.

[9]Petros A Ioannou,Jing Sun.Robust Adaptive Control[M].PTR Prentice-Hall,1996: 75-76.

[10]Xu L,Yao B.Adaptive Robust Control of Mechanical Systems with Non-linear Dynamic Friction Compensation[J].International Journal of Control,2008,81(2): 167-176.

[11]刘金琨.滑模变结构控制MATLAB仿真：基本理论与设计方法[M].北京:清华大学出版社,2015: 62-66.

[12]孙建民.一种汽车主动悬架系统模糊控制器设计及试验[J].振动与冲击,2005,24(1): 13-17.

Adaptive Sliding Mode Control for Semi-active Suspension

WANG Xin,SUN Li-ying
（School of Electrical Engineering,Liaoning University of Technology,Jinzhou 121001,China）

An adaptive sliding mode controller is designed based on vehicles’ semi-active suspension system containing parameter uncertainties and external interference.This method uses sliding mode control to reduce the influence of external disturbance and improves the chattering by using hyperbolic tangent function.The adaptive Backstepping method is used to track the uncertain parameters.The simulation results show its effectiveness.

vehicles; semi-active suspension; sliding mode control; adaptive Backstepping

TP273

A

1674-3261(2017)05-0296-06

10.15916/j.issn1674-3261.2017.05.005

2017-06-20

辽宁省教育厅重大科技平台项目(JP2016012)

王 新(1991-)，男，山东潍坊人，硕士生。

孙丽颖(1972-)，女，辽宁抚顺人，教授，博士。

责任编校：孙 林