风险指引型PSA应用的不确定性分析方法研究
2017-11-07黄志超初永越李虎伟钱晓明徐海峰
黄志超,初永越,李虎伟,钱晓明,依 岩,徐海峰
(环境保护部核与辐射安全中心 北京 100082)
风险指引型PSA应用的不确定性分析方法研究
黄志超,初永越,李虎伟,钱晓明,依 岩,徐海峰
(环境保护部核与辐射安全中心 北京 100082)
不确定性是这个世界上所有事物与生俱来的特征,本文深入探讨了核电厂PSA不确定性的来源及其分类,研究了参数的不确定性、建模的不确定性以及模型的不完备性的处理方法。结合风险指引型PSA应用相关技术导则、法律法规等文件中对不确定性的相关要求,分别给出了在风险指引PSA应用中此三类不确定性的分析方法和相关可接受准则。风险指引PSA应用的不确定性分析是应用申请中不可或缺的重要组成部分,可为综合决策者提供足够的技术支持。
参数不确定性;建模不确定性;模型不完备性;风险指引型PSA应用
1 引言
这个世界是确定的还是不确定的?这无论在科学界还是哲学界,都是一个长期争论的问题。爱因斯坦曾说“上帝不会和我们掷骰子”,以牛顿为代表的确定论科学,创造了给世界以精确描述的方法,只要知道初始条件,就能决定未来的一切,描绘的都是一幅幅完全精确的科学世界场景。但也没有完全拒绝所有的不确定性,只不过认为这是对初始条件的测量误差、人类认知的局限性和知识的不完备而造成的。也有科学家发出了不同的声音,玻耳兹曼则认为世界是概率演算的极致,麦克斯韦将随机性观点引入物理学,建立了统计力学;量子力学的出现更是极大地冲击了对原有世界的认知。这意味的不确定性是一种客观存在,与人类意识到与否并无关联。
在现实世界里,大部分现象都是不确定的,所谓确定的、规则的现象,只是在一定的前提和特定的边界条件下发生的,在局部或者较短时间内存在。不确定性也正是这个世界的魅力所在,只有不确定性本身是确定的,在这样的背景下,混沌科学、复杂性科学和不确定性人工智能才得以蓬勃发展。
随机性也称为偶然性,是指事件发生的条件与结果没有决定性的关系,事件的出现与否表现出不确定性质,可以用随机数学作为工具进行分析。随机性的意义我们在生物进化、遗传规律、概率论、贝叶斯理论和证据理论上可以很清晰地感受到。概率安全分析(PSA)正是基于概率论的发展演绎的系统分析工具,本文对PSA应用过程中的不确定性进行初步探讨,以期抛砖引玉。
2 不确定性的来源与分类
目前,在PSA的不确定性讨论中有两个术语,即随机不确定性和认知不确定性。尽管统计意义上的不确定性可以很精确的定义,但专家认为PSA中的随机不确定性和认知不确定性只是偶然性和不确定度的代名词。
偶然这个词源于拉丁词根,意思为运气游戏,大数据样本固有的随机性构成了PSA基本事件的参数不确定性。认知则是希腊知识单词的词根,认知的不确定性是由于知识匮乏所引起的。在PSA中认知不确定性反映了分析人员对模型预测的自信程度和对该模型本身的认知水平,因此通常分为建模的不确定性和模型的不完备性。因此,在PSA的不确定性分析中,一般将其分为如下三类:
• 参数的不确定性;
• 建模的不确定性;
• 模型的不完备性。
2.1 参数不确定性
PSA模型的基本参数如设备失效率、始发事件频率和人员失误概率等的数值与不确定性有关,并用这些参数来量化评价事故序列,它们都有一个典型特征,即这些参数都符合某一种特定的概率分布,这些分布参数表征了分析人员对这些数值在现有技术水平的置信程度。这些参数还体现了所有类似设备类的通用或电厂特定数据的潜在相互关系特征,这些参数的不确定性贡献也被描述为模型的不确定性。
2.2 建模不确定性
在PSA中,建模或认知的不确定性往往不能显化处理,模化PSA场景和现象的数学模型的不确定性来源主要如下:
1) 仅能对系统简化建模分析;
2) 建模的边界可能并不完整或准确。
模型通常是建立在大量的假设基础之上,尽管可采用不同的技术或方法对模型进行完善,对一个物理模型而言,模型的不确定性是一个可大或可小的研究领域;方法不成熟、数据缺乏测试和验证、网格大小和步进周期的近似处理也构成了不确定性的重要来源。
建模不确定性与参数不确定性的主要区别在于是否使用一个数值恒定或变化的数据代入模型计算,分析人员可用多种科学方法来评估参数的不确定性。PSA模型不仅包含了参数的不确定性,还包括这些参数本身的相互关系,这意味着建模不确定性远比参数的不确定性要复杂且更重要,但遗憾的是,目前尚无分析工具来量化分析建模不确定性。
通过更大范围的对建模的不确定性的统计学处理方法的调研,也有不少理论和方法可供参考,但尚无在核电厂PSA建模的不确定性分析中予以应用的案例。
2.3 模型不完备性
在我们试图对经常遇到的不确定性划分一个高级别的分类时,通常将认知的不确定性分为建模的不确定性和模型的不完备性。不完备的不确定性即是指未知的,尚未在模型中考虑,换句话说,模型的不完备性所指的不确定性是更无法用参数的不确定性和建模的不确定性来进行描述和评价,它更涉及分析范围的局限性以及玄乎未知的问题。
因范围问题引起的模型不完备的不确定性可以通过选择特定的评价范围来解决,可适当定义分析范围和详细程度加以控制,如采用技术标准、借鉴行业实践经验以及应用PSA模型开发和应用的技术手册等,这些手段可在一定程度上对PSA模型的不完备性给予较好的诠释。
3 RI-PSA应用对不确定性的要求
3.1 RG1.174(NNSA-0147)
在RG1.174中,PRA结果和可接受准则所用的都是点估计值,概率分布则来自输入参数和模型的不确定度的传递。
在对复杂系统建模时必须对随机不确定性和认知不确定性分别进行处理。随机不确定性的特点是其发生具有随机性或偶然性,适于采用概率模型来描述。正是该特征才使得PSA中有“概率”一词。认知不确定性则与分析者对PSA模型本身所预计的置信度有关,反映该PSA模型在多大程度上能代表所模化的真实系统。
3.2 RG1.200(NNSA-0159)
对PSA结果的理解中的一个重要方面就是需要理解与其相关的不确定性,识别影响PSA结果的因素及其来源。模型的敏感性分析结果来模化边界条件和用敏感性分析来评价一些假设。
与所模化分析的系统中的设备的失效概率和不可用度一样,参数估计中也要定量分析始发事件频率。评估过程要含进行不确定性分析的方法和具备将不同来源的数据,含电厂的实际运行经验和历史数据,采用一致的方法进行处理成具有通用性的数据源。
3.3 RG1.177(NNSA-0148)
与任何风险指引研究一样,TS变更的风险指引分析会受到各种与PSA模型建立和应用中所作假设有关的不确定性影响。在提交TS变更的申请材料中,需要对其中的重要假设进行敏感性分析,并开展不确定性分析。
3.4 ASME-Ra-Sa-2009
在PSA的ASME-Ra-Sa-2009中对PSA模型的各技术要素均提出了开展不确定性分析的需求,表1是部分表述。
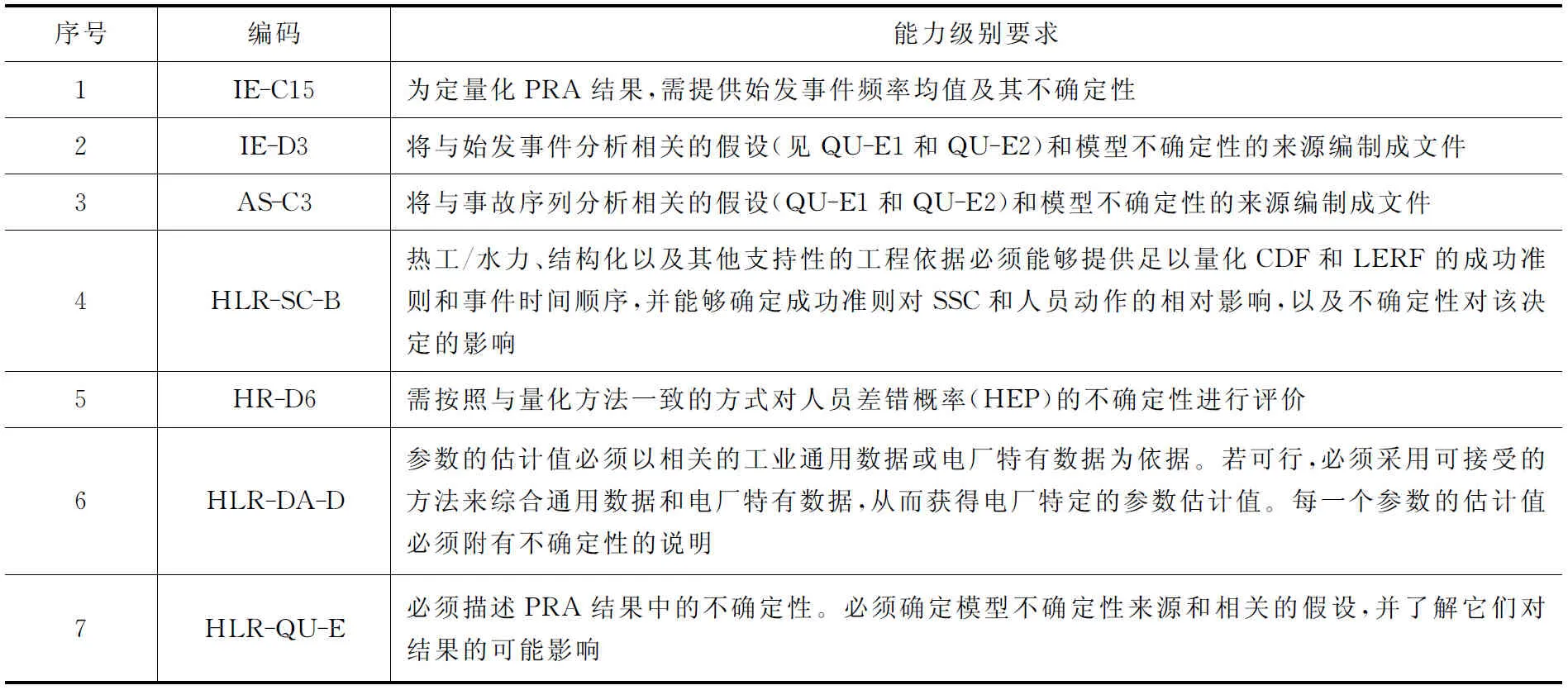
表1 ASME标准对不确定性分析的要求(部分)Table 1 Uncertainty Analysis Requirements of ASME Standard (Partial)

续表序号编码能力级别要求8HLR⁃LE⁃F必须审评量化的结果,必须确定LERF的重要的贡献因素,如电厂损伤状态、安全壳威胁和失效模式。必须确定模型不确定性来源和相关的假设,并理解它们对结果的可能影响
3.5 PSA应用技术政策声明
不确定性是核安全监管决策过程中必须考虑的问题。在确定论安全分析方法和概率安全分析方法中都存在不确定性,分析过程中存在的不确定性主要包括模型的完整性、模型的适当性和输入参数的不确定性三个方面。
总体而言,确定论安全分析方法没有提供评估不确定性的手段,仅在事故进程分析中希望通过保守的方式来处理某些不确定性,而概率安全分析方法可以定量地评价不确定性的影响,并通过敏感性分析和重要度分析等手段进行处理。与确定论安全分析相比较,概率安全分析一般更全面,对许多问题的处理更精细。不论使用哪种分析方法,都要考虑不确定性的存在,并对其进行适当处理。
不确定性并不是由于在决策过程中使用了概率安全分析技术而引起的,而仅仅是在概率安全分析的量化过程中被凸现出来了。随着概率安全分析技术的不断发展,概率安全分析技术提供了评估不确定性的定量化方法,重要的不确定性已经得到并且将继续得到更多的关注。
4 不确定性的处理方法
4.1 参数不确定性分析
参数的不确定性是指用来计算诸如始发事件频率、设备失效概率、人因失效概率的不确定性,这些参数均是用以定量化计算PSA模型。这些不确定性以分析者对这些参数值的取信程度的概率分布的形式予以表述。目前绝大部分PSA软件均能传播和计算PSA结果的这些概率分布。在进行风险指引型决策(RIDM)时,PSA的数值结果及其不确定性必须与相适应的决策导则比较。
在PSA模型中,其基本事件的参数主要来源频率统计、贝叶斯更新和专家判断,这也是参数不确定性的主要来源和评价方法。频率方法或经典估计方法是建立在大量试验的基础之上进行统计的结果,频率统计方法通常是给出一个点估计值,数学方法就为最大似然估计(MLE),给出点估计值及置信区间。贝叶斯方法则是在已知参数的数值和分布类型后结合现在已知信息的基础上得出最新的最可能数值及概率分布,该分布的均值通常作为参数的点估计值。贝叶斯方法提供了组合不同数据源的方法。专家判断方法则主要依赖于专家在该领域的技术知识和经验,给出一个参数或基本事件的“最佳估计值”。该方法主要在无法获取或缺乏相关证据时才被迫使用,比如确定罕见事件的概率/频率值。表2是贝叶斯方法和频率方法的特点。

表2 两种评价参数不确定性方法的特点Table 2 Characteristics of Two Methods for Evaluating Parameter Uncertainty
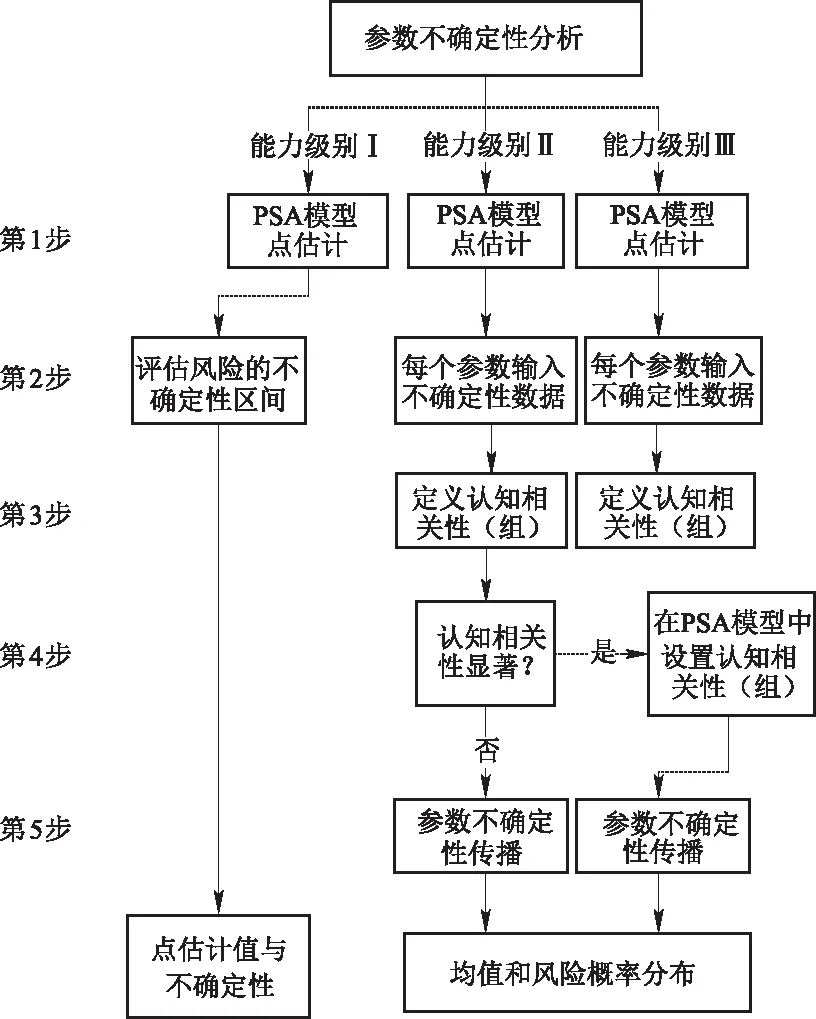
图1 参数不确定性分析步骤Fig.1 Parameter uncertainty analysis procedure
参数不确定性分析中要特别注意认知相关性(Epistemic Correlation,EC),在概率安全分析中,对于同一个核电站中相同或类似的设备,通常认为它们的失效参数(包括均值和概率分布)是相同且相关的(齐次性假设)。这种参数之间的相关性通常称为认知相关性。认知相关
性对PSA结果的影响是巨大的,仅以一个包含两个基本事件(如电动阀拒开,均值1E-4,满足对数正态分布,EF=5、10和100)的割集为例进行简要说明:
• 如果考虑参数之间的相关性,则该割集的均值为P(XY)=P(X2);
• 如果不考虑参数之间的相关性,则割集的均值为P(XY)=P2(X)
根据柯西不等式,不难证明P2(X)≤P(X2),表3是计算的结果。
一般而言,一个包含多个有相同参数基本事件的割集,考虑了参数之间认知相关性的不确定性均值结果,比不考虑相关性的均值结果要大,比各个基本事件均值的乘积(点估计值)要大得多,即P(Xn)>>Pn(x)。
表4给出了参数不确定性分析中采用敏感性分析方法的可接受准则。
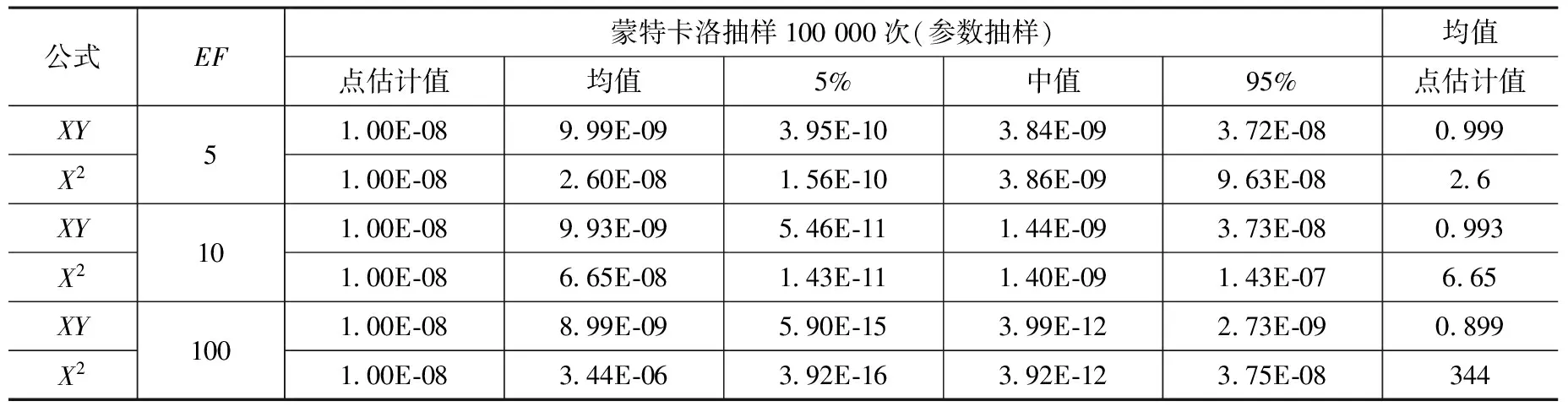
表3 认知相关性对割集结果的影响Table 3 Influence of Cognitive Correlation on Cut-set Results

表4 参数不确定性处理的敏感性可接受准则Table 4 Sensitivity Acceptance Criteria for Parameter Uncertainty Analysis

续表编号敏感性可接受准则PUNC⁃3b对于模型中同一割集里或共因组里存在三个有相关性的变量,则:1)如果范围因子RF≤5,则无论这三个变量各自对该风险的贡献(0到1),由相关性对总的风险影响小于10%;2)如果范围因子RF≤10,且如果这三个变量对总风险的贡献小于95%,则由相关性对总的风险影响仍小于10%;3)如果范围因子RF>10,对风险的贡献要限制的更严厉,如果,RF>30,则对风险的贡献要小于2%,以保持均值处于点估计值的±10%范围以内。PUNC⁃4采用不低于10000个样本进行蒙特卡洛抽样计算其均值,如果至少10000个样本不可取,则蒙卡抽样次数应至少选取到能得到一个较为稳定的均值数时为止。对于基准模型,尚无区分点估计均值和参数均值差异的准则。适用的准则:抽样计算的均值与点估计值相差10%以内,否则,就需要调研失效率的误差因子(EF)、额外开展电厂特定数据分析、共因和人因事件;如果点估计值比均值大(通常而言,点估计值都是大于均值的)10%,但在20%范围内,则应明白无误的记录下来差异的原因;在风险指引型PSA应用中要判断或考虑这些差别。如果仍大于20%,则必须开展特定电厂的设备可靠性数据分析,包括共因数据和人因数据。PUNC⁃5对已经在PSA模型中评价的参数不确定性和电厂特征进行比较,如果这二者差异很小或已判断得到有效补偿,则将结果报告中的5%和95%分位值作为整个风险的参数不确定性,并以误差形式记录在案。PUNC⁃6采用蒙特卡洛或类似方法进行不确定性传播分析,在模型中以布尔逻辑运算获得其相关性,并以5%和95%分位值作为风险的上下限,在报告中给出计算结果。采用不低于10000个样本进行蒙特卡洛抽样计算其均值,如果至少10000个样本不可取,则蒙卡抽样次数应至少选取到能得到一个较为稳定的均值数时为止。说明范围因子(RF)的定义是该参数的上限与下限的平方根,一般而言,如参数的置信区间为90%,则RF=2X95%X5%,如果参数满足对数正态分布,则RF=EF。
4.2 建模不确定性分析
模型的不确定性是指因在建模和简化时不可避免所做的假设的不确定性,如在压水堆中反应堆冷却剂泵因轴封冷却丧失而假设泵不可用,在PSA模型中的处理共因失效的方法以及人员可靠性分析中的方法。总的说来,模型的不确定性可通过对分析结果进行敏感性分析或类似分析方法来解决。
对PSA结果的理解中的一个重要方面就是需要理解与其相关的不确定性,识别影响PSA结果的因素及其来源。图2是识别和确定性建模不确定性和相关假设的主要来源的流程。

图2 识别模型的不确定性主要来源与关键假设流程Fig.2 The Process of Identify the main sources of model uncertainty and the key assumptions
模型的不确定性及其相关假设的主要来源一经确定,就可对这些不确定性来源的特征进行定性筛选。根据ASME的PSA技术标准,建模的不确定性识别主要可以从如下四个方面进行,图3对识别和确定模型不确定性和关键假设的特征流程进行了图示说明:
• 对PSA模型的影响,包括对单个基本事件、多个基本事件、事件树或故障树的逻辑结构以及基本事件与逻辑结构的组合情况。在PSA模型中主要有始发事件、系统、构筑物和设备(SSC)的不可用度和失效率、人误概率等基本事件,可以从这些方面逐一识别建模假设和不确定性的来源;
• 所使用的建模方法和假设,在这里可以识别出PSA建模方法和主要关键假设的不确定性来源;
• 对PSA结果的影响,如设备失效率、不可用度、始发事件频率、人误失效概率和共因失效等发生变化时对PSA的结果影响较大,此外,如果改变对某一现象的建模假设条件、成功准则等,这些因素都对PSA结果造成较大影响,可以通过开展敏感性或重要度分析来解决这些不确定性问题;
• 在构建模型时,为了简化或不能获得精确的数据时,不可避免地要进行一些偏于保守性的假设或取值,这都是构成PSA及其应用过程中不确定性的主要来源,可通过敏感性和重要度分析来进一步量化评价。

图3 识别建模不确定性主要来源与关键假设特征流程Fig.3 The Process of Identify the main sources of modeling uncertainty and the key assumptions
敏感性分析方法可以确定被识别出的不确定性来源和关键建模假设是否满足相关风险可接受准则,如RG11.174(NNSA-0147)或RG1.177(NNSA-0148)等。这些准则包括单一风险可接受准则和多个准则的组合。本文以仅单一基本事件受到影响,并以满足单一风险可接受准则为判据为例,对不确定性分析的结果进行保守性和现实性筛选。
(1) 保守性筛选
根据风险增加重要度RAW的定义可知:

(1)
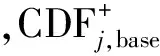
需要特别注意的是,公式(1)中的CDF是均值而不是点估计值。为满足风险可接受准则,存在一个最大接受的CDF数值,我们假定为5.0E-05/堆年,基准模型的CDF是3.0E-05/堆年,则最大允许的RAWmax为:

此时,必须满足:
RAWj,base≤RAWmax
(2)
(2) 现实性筛选
在保守性筛选中将基本事件的概率设为1,即该事件已经发生,设备失效或发生始发事件,这一假设与真实情况可能差异较大,因此公式(2)具备了太大的保守性,为此需要确定一个合理的基本事件概率值或始发事件频率来进一步确定是否为关键的不确定性。因此可以根据实际允许经验或专家判断取一个合理的数据进行计算是否满足风险可接受准则,也可以采用敏感性分析方法来进行现实性筛选。
4.3 模型的不完备性分析
参数的不确定性和建模的不确定性分析尽管复杂且工作需要详尽细致,但毕竟还是可以进行定性和定量评价的。模型的不完备则是在模型中尚未分析,或详细程度不足以得出较为精确的结果,因此需要评价尚未进行分析部分的风险(即剩余风险)对结果的影响,模型的不完备性不确定性分析可以采用定性筛选或保守估计进行评价,即:
(1) 通过升级PSA模型以扩大分析范围或提高详细程度;
(2) 通过筛选方法以确定所忽略的风险不会对结果造成显著影响;
(3) 使用保守方法,量化评估未在模型中详细分析的风险;
(4) 修改后未分析风险不会对风险指引型综合决策有明显影响。
在进行风险指引型PSA应用时,对因模型不完备可能引入的不确定性分析时,需要考虑如下因素:
• 是否引入新的始发事件?
• 是否需要对始发事件(组)进行修改?
• 是否影响系统成功准则?
• 是否需要增加新的事故序列?
• 是否新增SSC的失效模式?
• 是否对系统的可靠性或系统间的相关性有影响?
• 是否需要修改模型参数(含频率、失效率、人误概率等)?
• 是否引入新的共因失效机制?
• 对人误事件是否有减少、增加或更改?
• 是否会影响其他应用结果,比如重要度或措施?
• 是否可能存在安全壳旁通或失效,进而导致早期放射性大量释放?
• 是否影响SSC缓解其他外部事件,如地震等?
• 是否对低功率停堆等运行工况的系统/设备的可靠性有不利影响?
针对模型的不完备性引入的不确定性分析方法同样也可以采用敏感性分析方法、定性的从保守性和现实性进行筛选,本处不再赘述。
表5给出了建模不确定性和模型不完备性分析采用敏感性分析方法的可接受准则。

表5 建模不确定性和模型不完备性的敏感性可接受准则Table 5 Sensitivity Acceptance Criteria for Modeling Uncertainty and Model Incompatibility
5 RI-PSA应用的不确定性分析
美国NRC在概率风险评价的政策声明中鼓励更多的使用PSA技术来改善安全决策并提高监管效率,同时也给出了此类变更决策应该综合确定论和概率论,图4是在此框架下建立的风险指引综合决策的原则。

图4 风险指引综合决策的原则Fig.4 The Principle of the Risk-Informed Integrated Decision Making
根据图4所示的风险指引决策原则,NRC制定了评估执照基准变更的四要素法以支持NRC的决策过程,值得注意的是,该方法实际上是一个反复迭代的过程。虚框部分就是本文想要讨论的不确定性分析的部分(见图5)。

图5 风险指引综合决策过程的不确定性Fig.5 The Uncertainty of the Risk-Informed Integrated Decision Making Process
风险指引型PSA应用变更的申请所使用PSA的模型范围和详细程度必须足能支持,并对其不确定性进行必要的论证和说明。不确定性分析应包括参数的不确定性、建模不确定性和模型的不完备性。在申请报告中仅对风险评估结果的简单展示和与风险可接受准则的数字比较并不能足以说明其不确定性。因为所提供的风险结果无论是均值还是不确定性分布都只是说明了参数的不确定性,且并没有对其中关键的参数相关性(组)进行足够的论证。而建模不确定性和模型不完备性所含的剩余风险在已有的不确定性结果中无法体现。
6 结论
在风险指引综合决策的安全理念中,分析和处理不确定性都是综合决策过程中的重要组成部分,为了确保决策的正确性,则必须了解因不确定性对变更决策可能产生的影响,并与可接受准则进行比较。
参数不确定性,特别是参数的认知相关性可能对概率安全分析的结果有着重要影响。本文详细地对参数不确定性的分析方法、可接受准则进行了示例说明,并对建模不确定性和模型的不完备性所含的不确定性分析方法与敏感性方法可接受准则进行了研究。对于提高对不确定性的认识和系统评价不确定性提供了技术参考。同时也希冀本文能提高大家对不确定性研究的兴趣,以促进国内PSA技术发展和得以更广泛的应用。
[1] Treatment of Parameter and Modeling Uncertainty for Probabilistic Risk Assessments,EPRI,K.Canavan,2008.11,1016737.
[2] Guideline for the Treatment of Uncertainty in Risk-Informed Applications:Technical Basic Document,EPRI,Palo Alto,CA:2004. 1009652.
[3] Guideline for the Treatment of Uncertainty in Risk-Informed Applications:Applications Guide,EPRI,Palo Alto,CA:2004. 1013491.
[4] American Society of Mechanical Engineers,Standard for Probabilistic Risk Assessment for Nuclear Power Plant Applications,ASME RA-Sb-2005,New York,2010.11.
[5] US. Nuclear Regulatory Commission,An Approach for Determining the Technical Adequacy of Probabilistic Risk Assessment Results for Risk-Informed Activities,RG 1.200,Revision 1,2007.1.
[6] US. Nuclear Regulatory Commission,An Approach for Using Probabilistic Risk Assessment in Risk-Informed Decision on Plant-Specific Changes to Licensing Basis,RG 1.174,Revision 1,2007.1.
[7] Parametric Uncertainty Impacts on Option 2 Safety Significance Categorization,EPRI,1008905,2003.6.
[8] Guidance on the Treatment of Uncertainties Associated with PRAs in Risk-Informed Decision Making,NUREG-1855,2009.3.
UncertaintyAnalysisinRisk-InformedProbabilisticSafetyAssessmentApplications
HUANGZhi-chao,CHUYong-yue,LIHu-wei,QIANXiao-ming,YIYan,XUHai-feng
(Nuclear and Radiation Safety Center,MEP,Beijing 100082,China)
Uncertainty is one of the inherent characteristics for all of the world things. This paper discussed in-depth the sources of uncertainty and their categories for nuclear power plant PSA,and provided guideline on the treatment of the processing and methodology of the parametric uncertainty,modeling uncertainty,and completeness uncertainty. Combination with the risk acceptance criteria,PSA application-related technical documents,regulations requirements,guidelines and other standards,given the three uncertainty analysis methods and associated acceptance criteria. Uncertainty analysis has become an important part and basis of the integrated decision-making,provided adequate confidence and technical supports for the decision-makers.
Parametric uncertainty;Modeling uncertainty;Completeness uncertainty;Risk-Informed PSA application
2016-09-11
黄志超(1978—),男,湖南邵阳人,高级工程师,硕士,从事核电厂概率安全分析和严重事故评价工作
徐海峰:xuhaifeng@chinansc.cn
TL48
A
0258-0918(2017)05-0830-09
