障碍空间中基于Voronoi图的组反k最近邻查询研究
2017-11-07张丽平郝晓红郝忠孝
张丽平 刘 蕾 郝晓红 李 松 郝忠孝,2
1(哈尔滨理工大学计算机科学与技术学院 哈尔滨 150080)
2 (哈尔滨工业大学计算机科学与技术学院 哈尔滨 150001)
(zhanglptg@163.com)
随着基于位置服务技术的广泛应用,空间数据库中的最近邻(nearest neighbor, NN[1])查询及它的变体查询成为热点问题.近年来,最近邻查询的研究进一步拓展到反向最近邻查询[2]、组最近邻查询[3]、可视最近邻查询[4]、可视反向k最近邻查询[5]、不确定数据集中的k最近邻查询[6]、强邻近对查询[7]、连续反k最近邻查询[8]、聚集最近邻查询[9-10]、双色数据集上的反向最近邻查询[11]、移动k最近邻查询[12]等方面.所取得的成果解决了最近邻查询领域的一些重要问题.
反k最近邻(reverseknearest neighbor, RkNN[8])查询是空间数据库中的重要的查询之一,在空间决策支持、资源分配和数据挖掘方面有着广泛的应用.RkNN查询获得将查询对象作为k最近邻的数据对象集合,可以反映出该查询对象对哪些空间对象影响较大,所以一般用来评估查询对象的影响力.例如,在一家商场的选址工作中,需要评估该商场对附近哪些人群有影响力,该商场所吸引的顾客群就是RkNN查询所要找的影响集.由于此类查询可以支持高级的分析和预测应用,因此在实际应用中已经变得越来越重要.对于RkNN查询,文献[13]提出了一种新的双色反向最近邻查询,该查询利用基于网格的方法对空间对象进行聚类,同时利用B+树进行索引方向角,来达到有方向性的查询.根据实际需求,有时需要对一个商业区进行评估影响力,即查询一组查询对象的RkNN结果,因此宋晓宇等人提出了组反k最近邻(group reverseknearest neighbor, GRkNN[14])查询.该查询方法通过计算查询对象的最小覆盖圆,将圆中的对象作为一个整体来计算该组查询点RkNN的搜索区域.
以上查询均是在理想的欧氏空间中,但是现实空间中不可避免会有一些地理条件的限制(例如建筑、河流、山等),因此2个对象之间的最短距离必须考虑障碍物的因素.对于障碍空间中的查询,于晓楠等人[15]提出了一种障碍空间中的反k最近邻查询方法,该方法利用障碍Voronoi图的性质设计了高效的剪枝策略,可以大幅度地减少搜索障碍反k最近邻对象的时间和空间.Gao等人[16]引入一种新的边界区域的概念,可以有效地处理障碍反k最近邻查询.杨泽雪和郝忠孝[17]提出空间数据库中的组障碍最近邻查询.在障碍空间中,现有的空间查询研究成果只涉及到障碍最近邻查询、障碍反向最近邻查询、障碍组最近邻查询、障碍反k最近邻查询等方面,并没有涉及障碍组反k最近邻查询问题.因此,障碍空间中的组反k最近邻查询问题是一个新的需要解决的问题.
为了解决障碍空间中的组反k最近邻查询问题,基于Voronoi图,本文提出了障碍空间中的GRkNN查询方法(OGRkNN查询方法).该方法获得的结果集是将这组查询点中任意一点作为障碍k最近邻的数据点集合.查询中将GRkNN查询中的欧氏距离度量改为障碍距离度量.在实际应用中可以用来评估一组查询对象的影响力.本文依据障碍物集合是否发生变化分2种情况讨论OGRkNN查询方法:1)静态障碍物环境下的OGRkNN查询方法(简称STA_OGRkNN查询方法);2)动态障碍物环境下的OGRkNN查询方法(简称DYN_OGRkNN查询方法).其中STA_OGRkNN查询方法包括2个过程:剪枝过程和精炼过程.利用Voronoi图的邻接特性可以在剪枝阶段和精炼阶段有效地过滤掉大量的非候选者,快速地缩小查询范围,提高整个算法的查询效率.进一步给出了3种情况下的DYN_OGRkNN查询方法.
1 定义与定理
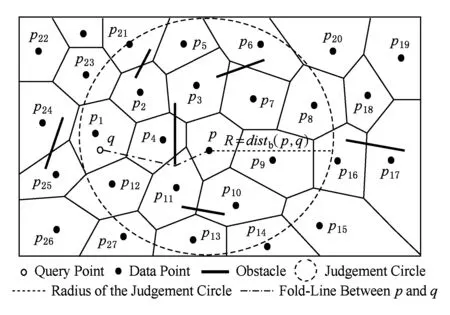
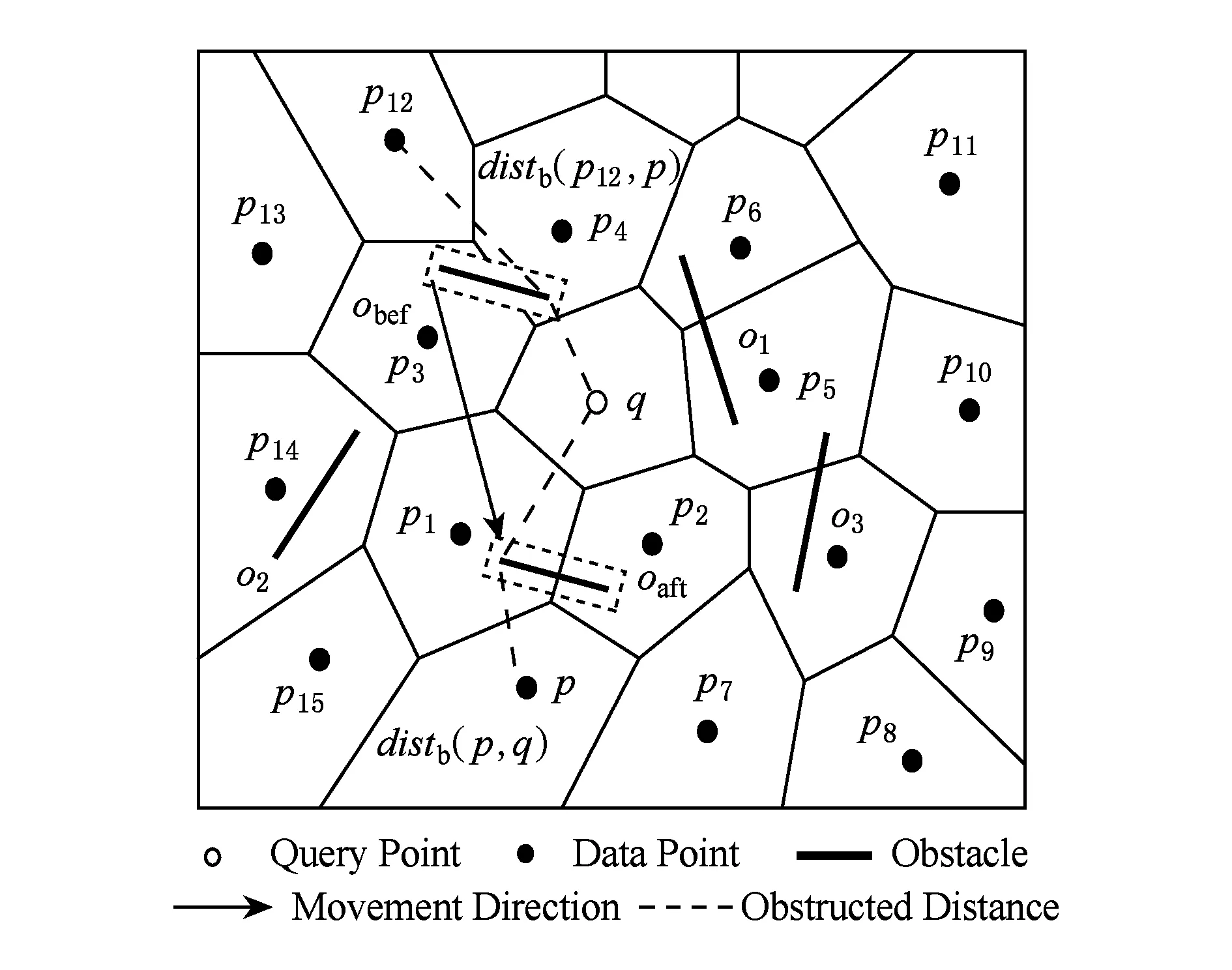
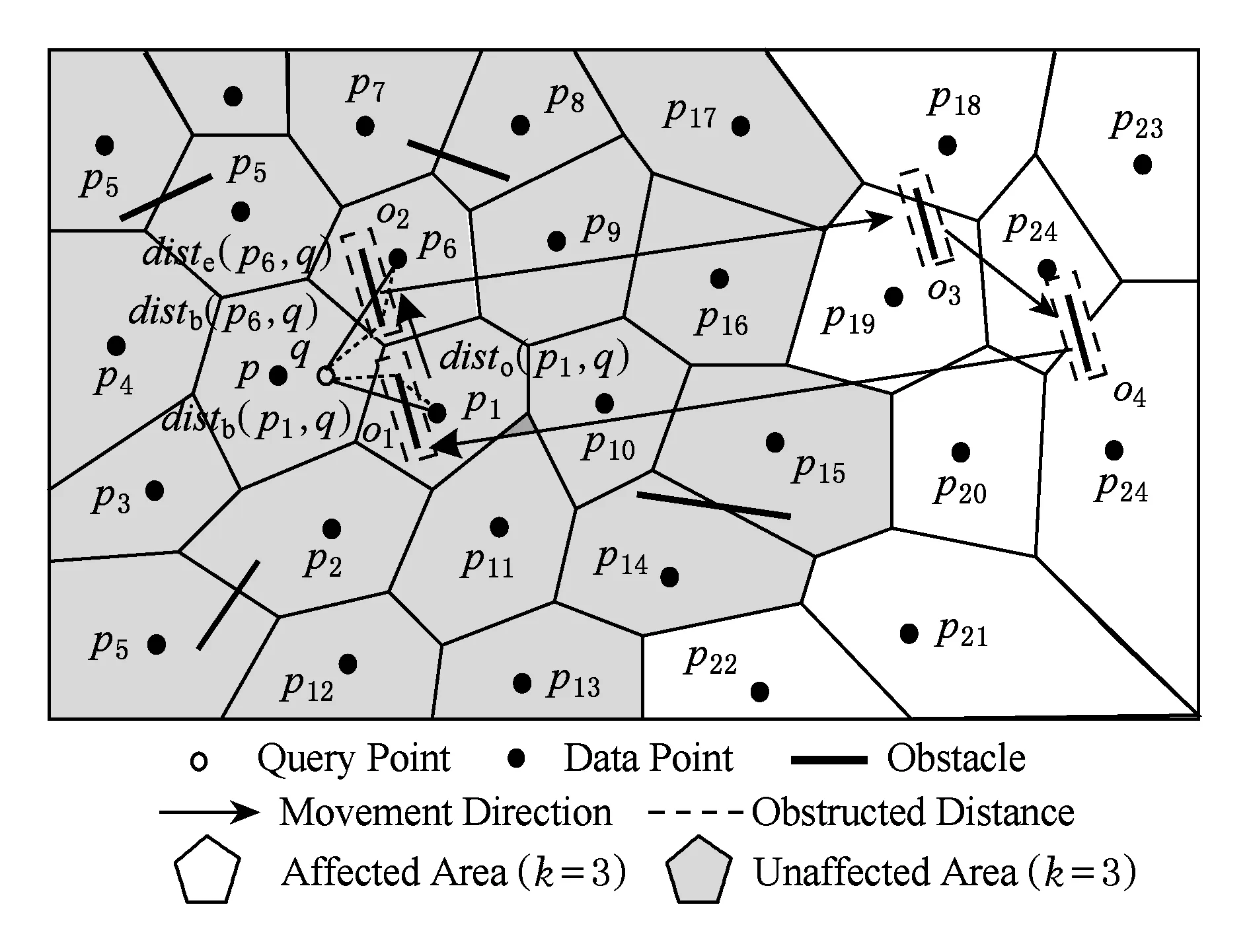
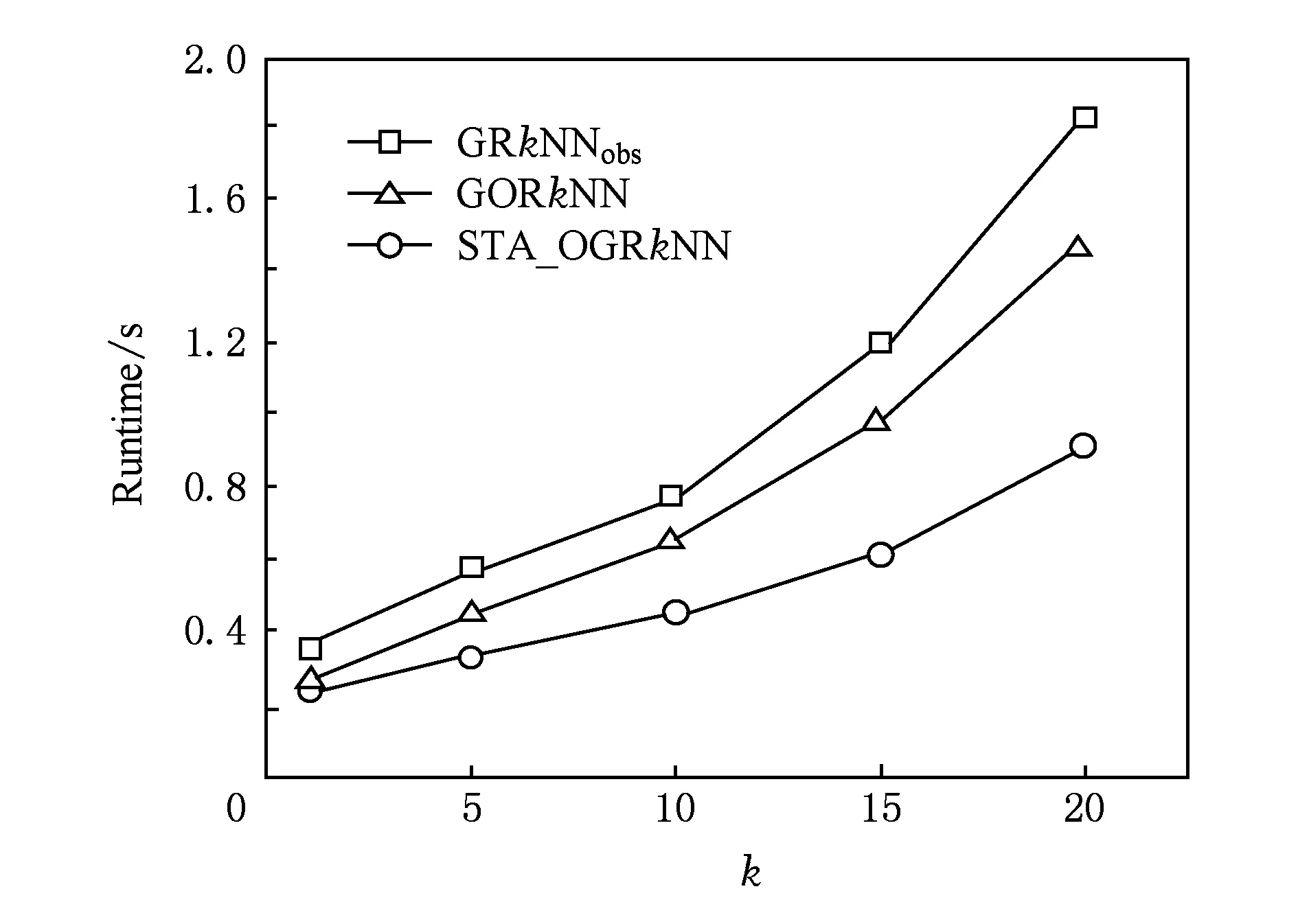
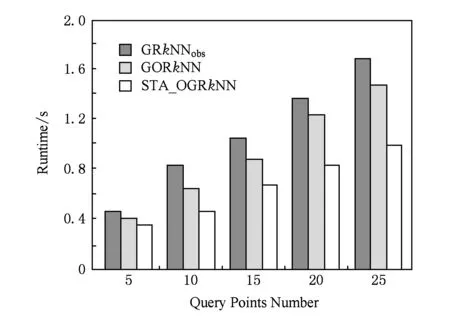
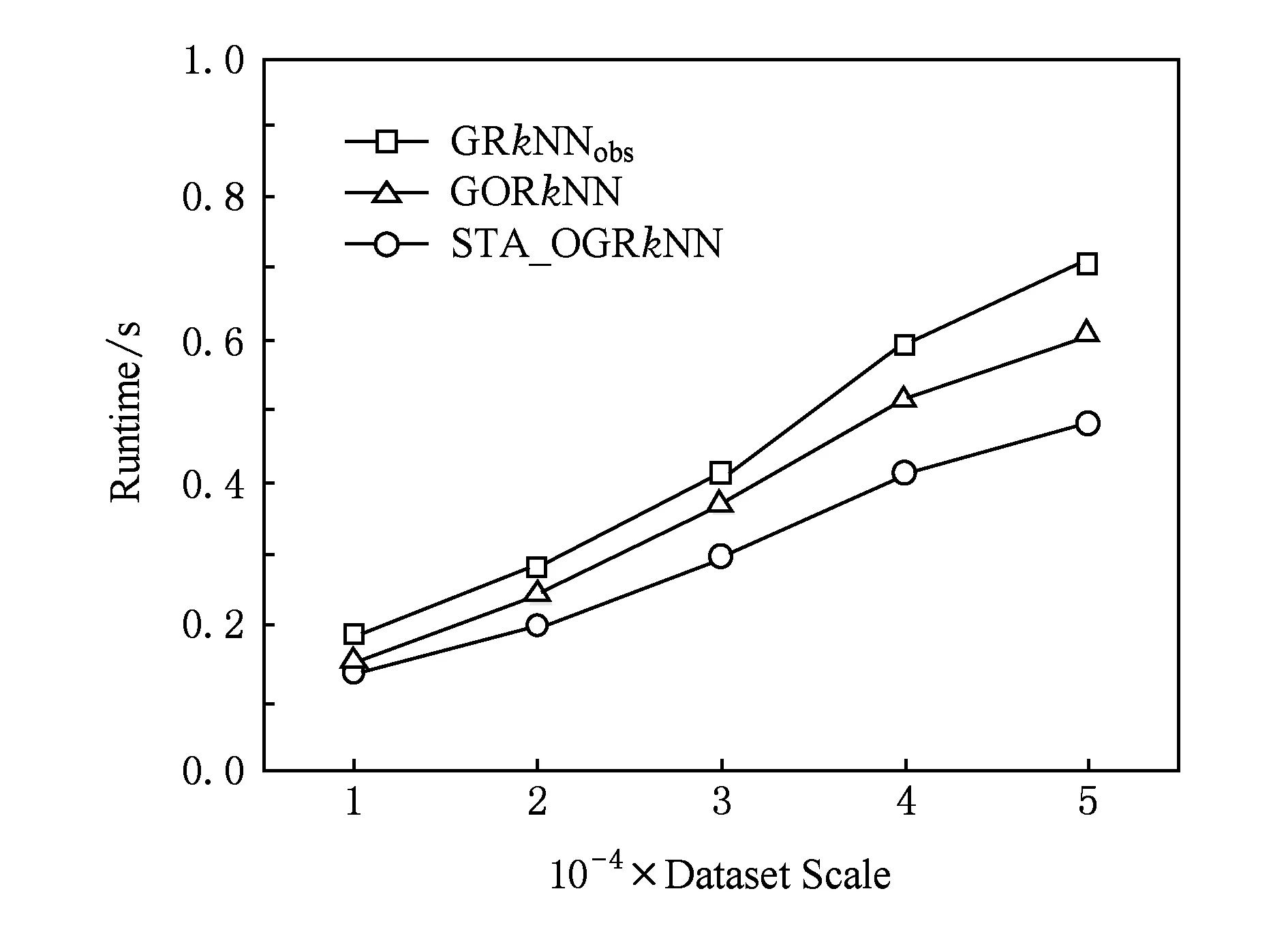
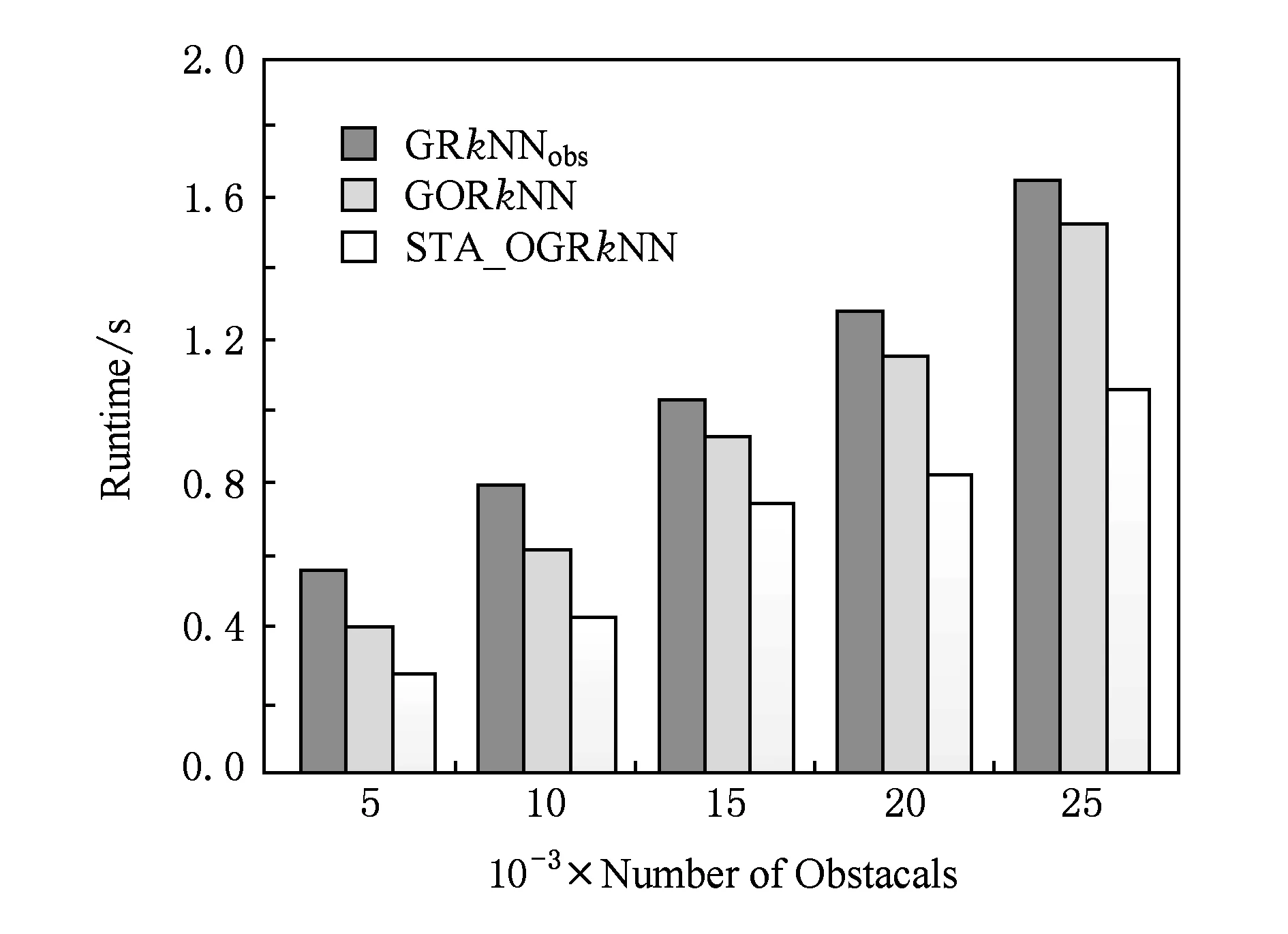
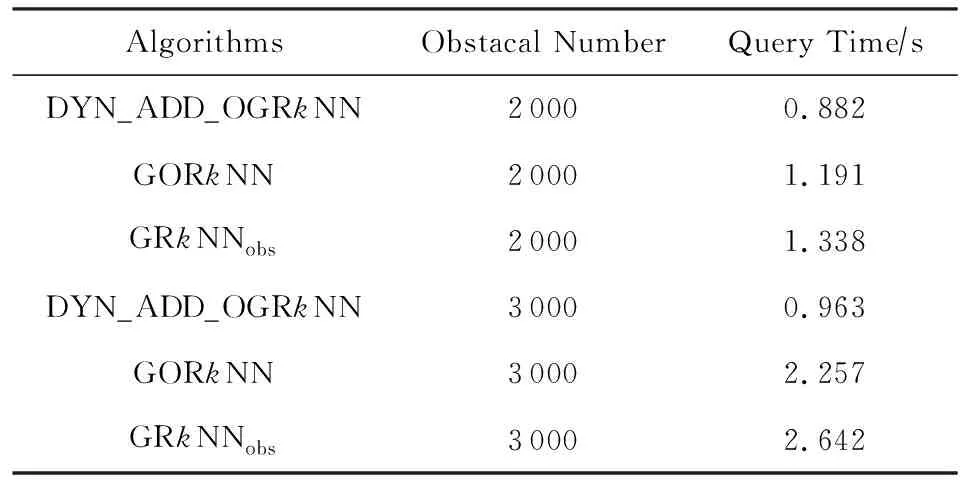
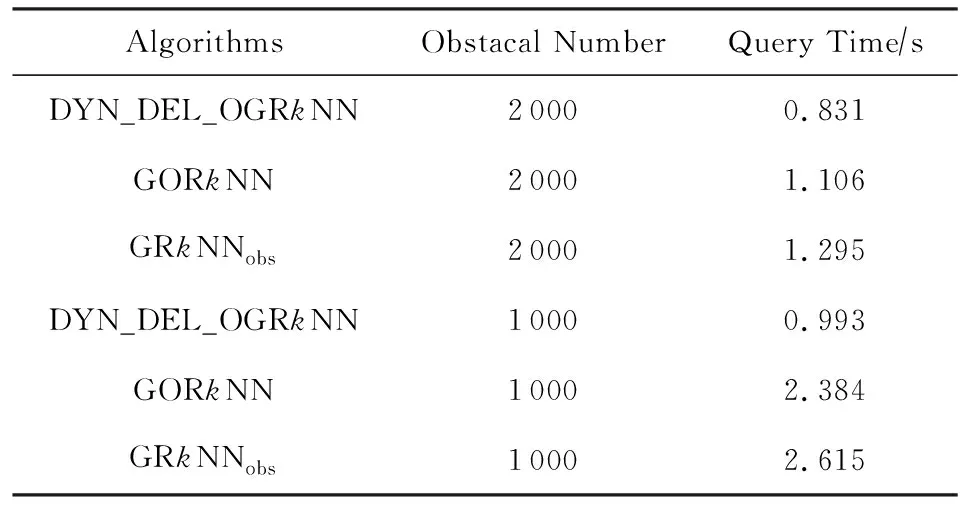
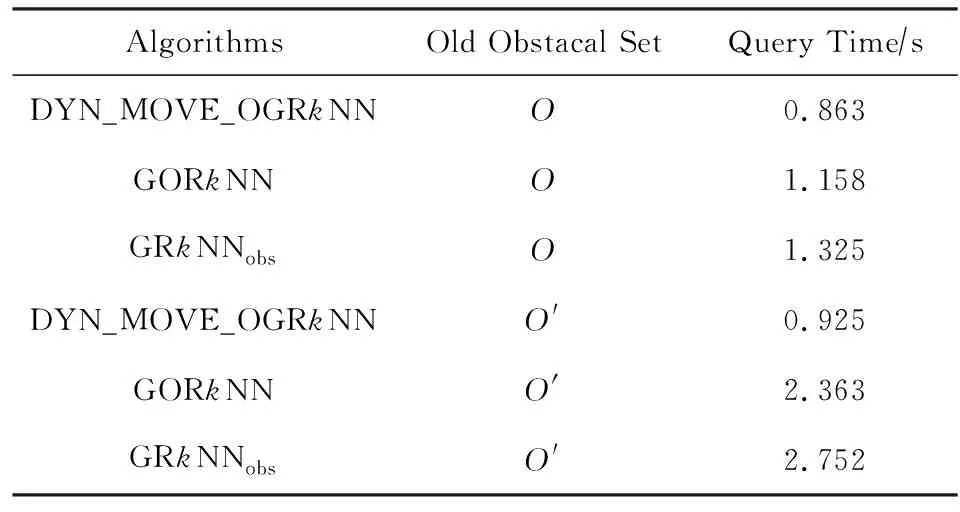
定义1. Voronoi图[18].给定一组生成点P={p1,p2,…,pn},其中2 定义2. Voronoi图的k级邻接生成点[18].给定一组生成点P={p1,p2,…,pn},生成Voronoi图,其中2 1) 1级邻接生成点 AG1(pi)={pj|VP(pi)和VP(pj)有公共边}; 2)k(k≥2)级邻接生成点 AGk(pi)={pj|VP(p)和VP(pj)有公共边,p∈AGk-1(pi)}. 定理1[18]. 点q为Voronoi单元VP(pi)内任一点,pk+1∈AGk+1(pi).那么必存在一点pk∈AGk(pi)使得dist(q,pk)≤dist(q,pk+1). 定理2[18]. 对于Voronoi多边形VP(pi)内任一点q,q到pi的k级邻接生成点的最小距离小于到任何pi的k+1级邻接生成点的距离(k为整数,k≥1). 定理3[18]. 对于Voronoi多边形VP(pi)内任一点q,q的第k+1个最近邻qk+1有qk+1∈AG1(p)∪AG2(p)∪…∪AGk(p)(k为整数,k≥1),即q的第k+1个最近邻在q的最近邻前k级邻接生成点中. 基于点与点的可视性[18]﹑点与点的障碍距离[19]和组反k最近邻查询[14]的基本概念,本文进一步提出了障碍组反k最近邻查询的定义如定义3所示. 定义3. 障碍组反k最近邻查询.在障碍空间中,给定一组查询点集Q={q1,q2,…,qn}和一个数据点集P={p1,p2,…,pm},在数据集P中查询那些k个最近邻中包含Q中任意一个查询点q的空间数据点,具体定义形式为 OGRkNN(Q,P,k,O)= 本节提出的STA_OGRkNN查询方法主要分为剪枝过程和精炼过程2个步骤.首先通过剪枝可以过滤掉大量的非候选者以及对查询没有影响的障碍物,再对候选集进行精炼处理获得准确的结果集. 剪枝过程中首先计算查询点集Q的质心q,用质心q近似地代表查询点集整体.实际应用中,查询点集是一组邻近的对象,故可以用质心近似地代表查询点集.然后根据剪枝策略对数据点及障碍物进行剪枝,剩下的未被剪枝的数据点构成候选集,未被剪枝的障碍物构成新的障碍集. 定理4.q的RkNN只在NN(q)的前k级邻接生成点中,故NN(q)的第k级及k级以外的邻接生成点和障碍物被剪枝. 证明. 由定理3可知,q是Voronoi多边形内任意一点,设q的最近邻为p,则对q的第k+1个最近邻qk+1有qk+1∈AG1(p)∪AG2(p)∪…∪AGk(p),(k为整数,k≥1),即q的第k+1个最近邻在p的前k级邻接生成点中.则显然有qk∈AG1(p)∪AG2(p)∪…∪AGk-1(p),即q的第k个最近邻在p的前k-1级邻接生成点中.故p的第k级及高于k级的邻接生成点中不可能存在q的kNN.若pj∈AGn(p)(n>k),即pj是p的高于k级的邻接生成点,则反过来同理,p是pj的高于k级的邻接生成点.根据定理3,pj的kNN不包括p,也就是q的RkNN不包括pj.当存在障碍物时,pj到q的障碍距离一定大于等于它们之间的欧氏距离,故q的RkNN更不可能包括pj.因此,在障碍空间中,q的RkNN只在q的最近邻的前k级邻接生成点中,因此只保留q的最近邻的前k级邻接生成点及在前k级邻接区域内的障碍物. 证毕. 定理5. 设p在NN(q)的第n级邻接生成点中,即p∈AGn(NN(q)).p到q的路径上经过若干数据点pi,令单条路径上pi的总个数不大于n,将与p可视的pi总个数记作sumcount(p,q),如果sumcount(p,q)≥k,则数据点p被剪枝. 证明. 设p到查询点q的路径上经过的数据点为pi,当k=1时,则p到q的路径最多只经过1个数据点pi,若p对pi是可视的,则一定有diste(p,pi) 证毕. 定理6. 若p∈Sc且它的1级邻接生成点均被剪枝,则数据点p被剪枝. 证明. 设p为候选集合中的一点(p∈Sc),a为p的1级邻接生成点之一(a∈AG1(p)),且a是p到q路径上经过的点.若p的1级邻接生成点均被剪枝,显然a也被剪枝,即sumcount(a,q)≥k,那么一定有sumcount(p,q)≥k+1.由于sumcount(p,q)>k,则根据定理5,p被剪枝. 证毕. 本节提出的剪枝算法的主要思想为:通过定理4~6这3个剪枝策略,剪枝掉大量的非候选者以及对查询无影响的障碍物,获得候选集合Sc.这一过程中首先以数据点集P为生成点生成Voronoi图.然后计算查询点集Q的质心q,并用质心q近似地代表查询点集整体.再根据定理4,将NN(q)的前k级邻接生成点放入候选集合Sc中,高于k级的邻接生成点不可能是q的RkNN,因此被剪枝,进而获得初步的候选集,同时获得剪枝后的新障碍集.根据定理5,6对候选集中的数据点进行判断,满足条件的数据点被剪枝,剩下的未被剪枝的数据点构成更精确的候选集.基于以上讨论,进一步给出剪枝算法,如算法1所示: 算法1.STA_OGRkNN_Filter(Q,P,O,k). 输入:查询点集Q、数据点集P、障碍物集O、k值; 输出:候选集Sc、剪枝后的障碍集Onew. Create_Voronoi(P);*以P中数据点为生成点创建Voronoi图* Sc←∅;*初始化候选集Sc为空集* o∈O; count←0;sumcount←0; q←Calculate_Centroid(Q);*计算查询点集Q的质心q* ifq∈VP(p) then NN(q)←p;*q的最近邻是数据点p* fori=1 tokdo Sc←Sc+AGi(p);*将p的第i级邻接生成点集加入Sc中* endfor endif for eachp′∈Scdo ifVP(p′)∩o≠∅ then Onew←Onew+o;*剪枝障碍物* endif ifcount≤nthen for eachpi∈Path(p′,q)*pi是p′到q路径上的点* if [p′,pi]∩Onew=∅ do sumcount←sumcount+1; endif ifsumcount≥kthen Sc←Sc-p′;*定理5* endif endfor endif endfor for eachp″∈Scdo ifAG1(p″)∩Sc=∅ then Sc←Sc-p″;*定理6* endif endfor returnSc,Onew. 在精炼过程中,首先根据定理7对候选集Sc中的候选点进行精炼处理,得到更精确的候选集;再根据OGRkNN的定义对候选集中的点逐一排除,获得准确的结果集. 定理7. 当p∈Sc且p对查询点q是可视的,则以p点为圆心、以diste(p,q)为半径画圆,将该判定圆内p可视的数据点的个数记作count_points,若count_points≥k,则数据点p被剪枝.当p对查询点q是不可视时,以p点为圆心、以distb(p,q)为半径画圆,同样,若count_points≥k,则数据点p被剪枝. 证明. 分2种情况: 1) 当p∈Sc且p对查询点q是可视的时候,如图1所示.以p点为圆心、以diste(p,q)为半径画圆,则在判定圆内的数据点有{p1,p2,p3,p4,p5,p6,p7},其中{p1,p3,p6}对p是不可视的,{p2,p4,p5,p7}对p是可视的,则count_points=4.当k=4时,显然p的4NN是{p2,p4,p5,p7},而不包括q.当k<4时,由于数据点{p2,p4,p5,p7}到p的距离均小于q到p的距离,故p的kNN是{p2,p4,p5,p7}中的k个,一定不包括q,故q的RkNN一定不是数据点p,因此p被剪枝. Fig. 1 Proof 1 of theorem 7图1 定理7的证明情况1 2) 当p∈Sc且p对查询点q是不可视的时候,如图2所示.以p点为圆心、以distb(p,q)为半径画圆,则在判定圆内的数据点有{p1,p2,p3,p4,p5,p6,p7,p8,p9,p10,p11,p12,p13},其中{p1,p2,p4,p6,p12,p13}对p是不可视的,{p3,p5,p7,p8,p9,p10,p11}对p是可视的,则count_points=7.当k=7时,显然p的7NN是{p3,p5,p7,p8,p9,p10,p11},而不包括q.当k<7时,由于数据点{p3,p5,p7,p8,p9,p10,p11}到p的距离均小于q到p的距离,故p的kNN是{p3,p5,p7,p8,p9,p10,p11}中的k个,必不包括q,故q的RkNN不是数据点p,因此p被剪枝. 证毕. Fig. 2 Proof 2 of theorem 7图2 定理7的证明情况2 下面给出精炼算法,如算法2所示. 算法2.STA_OGRkNN(Q,P,O,k). 输入:查询点集Q、数据点集P、障碍物集O、k值; 输出:静态障碍物环境下的查询结果集SR. count_points←0; o∈Onew; Sc←STA_OGRkNN_Filter(Q,P,O,k);*调用算法1得到初步过滤后的候选集* for eachp∈Scdo if [p,q]∩o=∅ then CR←Circle(p,diste(p,q)); else CR←Circle(p,distb(p,q)); endif ifpoint∈CRand [point,p]∩o=∅ then count_points←count_points+1; ifcount_points≥kthen endif endif endfor kNN(p)←{p1,p2,…,pk}; if[p,pi]∩o=∅ then distb(p,pi)←diste(p,pi); endif fori=1 tokdo ifdistb(p,pi)≥distthen dist←distb(p,pi); pk←pi;*p的第k个最近邻为pk* endif endfor ifdistb(p,q)>distb(p,pk) then endif endfor returnSR. 由于现实生活中的障碍物不是静止不变的,所以本节进一步给出动态障碍物环境下的OGRkNN查询方法. 根据新增加的障碍物所在的位置,分2种情况讨论:1)新增加的障碍物对算法2的查询结果没有影响;2)有影响.根据定理4,q的最近邻的第k级及以外的邻接生成点和障碍物被剪枝,故将NN(q)的前k级邻接区域称为影响区域,用Affected_Area表示.设新增加的障碍物为o′,当o′∉Affected_Area时,由于在过滤过程中根据定理4会对影响区域以外的数据点以及障碍物进行剪枝,此时o′会一同被剪枝,所以o′对算法2的查询结果无影响.当o′∈Affected_Area时,设增加o′之前q的RkNN为{pi},若o′对[q,pi]造成阻断,则distb(q,pi)=diste(q,o′)+diste(o′,pi),显然有distb(q,pi)>diste(q,pi),故pi不再是q的RkNN;若o′对[q,pi]没有造成阻断,则o′对查询结果无影响. 基于以上讨论可得出判定规则1和判定规则2. 判定规则1. 设新增加的障碍物为o′,若o′∉Affected_Area,则对算法2的查询结果没有影响;若o′∈Affected_Area,则需要对算法2的查询结果集进行再判断. 判定规则2. 障碍物动态增加情况下的OGRkNN查询结果集一定是静态障碍物环境下的OGRkNN查询结果的子集. 根据判定规则1和判定规则2,本节提出的障碍物动态增加情况下的OGRkNN查询方法的主要思想为:首先判断新增加的障碍物的位置,然后计算受影响区域范围.根据判定规则1和判定规则2进行判断,若新增障碍物不在影响区域内,则返回静态障碍物环境下的查询结果;若新增障碍物在影响区域内,则对结果集中的数据点进行判断.若p到q的障碍距离大于p到它的第k个最近邻的障碍距离,则说明在新增加障碍物之后p不再是q的反k最近邻,故p被删除,最后剩下的数据点就是障碍物动态增加情况下的查询结果. 基于以上讨论,进一步给出障碍物动态增加情况下的查询算法,如算法3所示. 算法3.DYN_ADD_OGRkNN(Q,P,O,k,o′). 输入:查询点集Q、数据点集P、障碍物集O、k值、新增加的障碍物o′; 输出:障碍物动态增加情况下的查询结果集Snew. O′←O∪o′;*O′为新增加障碍物之后的障碍集* Affected_Area←∅;*受影响区域初始化* SR←STA_OGRkNN(Q,P,O,k); Judge_Position(o′);*判断新增加的障碍物的位置* ifo′∩Affected_Area=∅ then*新增障碍物不在影响区域内* Snew←SR; for eachp′ inSRdo if[p′,q]∩O′=∅ then distb(p′,q)←diste(p′,q); endif SR←SR-p′; endif endfor Snew←SR; endif returnSnew. 根据减少的障碍物所在的位置,分2种情况讨论:1)新增加的障碍物对算法2的查询结果没有影响;2)有影响.设减少的障碍物为o′,当o′∉Affected_Area时,由于在过滤过程中根据定理4会对影响区域以外的数据点以及障碍物进行剪枝,此时o′会一同被剪枝,所以o′对算法2的查询结果无影响;当o′∈Affected_Area时,设减少o′之前q的RkNN为{pi},若[q,pi]原来是阻断的,减少o′之后变成可视的,则q和pi之间的距离由障碍距离变成了欧氏距离,则有diste(q,pi) 基于以上讨论给出判定规则3. 判定规则3. 设减少的障碍物为o′,若o′∉Affected_Area,则对算法2的查询结果没有影响;若o′∈Affected_Area,则需将障碍集去除o′后再进行查询. 基于判定规则3,本节提出的障碍物动态减少情况下的OGRkNN查询算法的主要思想为:首先判断减少的障碍物所在的位置,然后计算受影响区域范围,根据判定规则3,将减少的障碍物是否在影响区域内分为2种情况.若不在影响区域内,说明减少的障碍物对算法2的查询结果不构成影响;若在影响区域内,则将算法2中的障碍集替换成减少障碍物之后的新障碍集,最后通过调用算法2得到障碍物动态减少情况下的查询结果. 基于以上讨论,进一步给出障碍物动态减少情况下的查询算法,如算法4所示. 算法4.DYN_DEL_OGRkNN(Q,P,O,k,o′). 输入: 查询点集Q、数据点集P、障碍物集O、k值、减少的障碍物o′; 输出: 障碍物动态减少时的查询结果集Snew. O′←O-o′;*O′为减少障碍物之后的新障碍集* Affected_Area←∅;*受影响区域初始化* Judge_Position(o′);*判断减少的障碍物的位置* ifo′∩Affected_Area=∅ then*减少的障碍物不在影响区域内* SR←STA_OGRkNN(Q,P,O,k); SR←STA_OGRkNN(Q,P,O′,k);*更新障碍集后再进行查询* endif Snew←SR; returnSnew. 本节主要研究的是障碍物动态移动情况下的OGRkNN查询方法.如图3所示,虚线箭头指向的是移动方向,原障碍集为{o1,o2,o3,obef},obef为发生移动的障碍物.在obef移动之前,q的R6NN包括p而不包括p12;障碍物obef移动之后,障碍集变为{o1,o2,o3,oaft},oaft为移动之后的障碍物,q的R6NN包括p12而不包括p.在障碍物移动前后的OGRkNN查询结果发生变化,故障碍物动态移动情况下的OGRkNN查询方法具有较高的研究价值. Fig. 3 Example about dynamically moving obstacles图3 障碍物动态移动示例 为了判断移动的障碍物对查询结果是否产生影响,首先判断发生移动的障碍物移动前后所在的位置,分别记为obef和oaft;然后根据obef和oaft的位置是否在影响区域内分为4种情况: 1) 障碍物在影响区域外发生移动,即obef和oaft均在Affected_Area外.例如图4中o3移动到o4. 2) 障碍物在影响区域内发生移动,即obef和oaft均在Affected_Area内.例如图4中o1移动到o2. 3) 障碍物从影响区域内移动到影响区域外,即obef在Affected_Area内,oaft在Affected_Area外.例如图4中o2移动到o3. 4) 障碍物从影响区域外移动到影响区域内,即obef在Affected_Area外,oaft在Affected_Area内.例如图4中o4移动到o1. Fig. 4 Example of obstacle movement图4 障碍物移动的示例 情况1中的obef和oaft均在Affected_Area外,根据定理4会对Affected_Area以外的数据点以及障碍物进行剪枝,此时obef和oaft会一同被剪枝,所以情况1对STA_OGRkNN查询结果无影响.情况2中的obef和oaft均在Affected_Area内,设障碍物移动前q的RkNN为{pi},pm,pn∈{pi},若[q,pm]原来是阻断的,[q,pn]是可视的,障碍物移动之后[q,pm]变成可视的,[q,pn]变成阻断的,则pm有可能不再是q的RkNN,而pn有可能变成q的RkNN,说明障碍物移动后会对查询结果产生影响.若障碍物的移动对[q,pi]的可视性不产生影响,则对查询结果无影响.由于情况2的不确定性,故需更新障碍集后再进行查询.情况3中obef在Affected_Area内,同情况2一样对查询结果可能有影响,oaft在Affected_Area外,对查询结果无影响,故也需更新障碍集.同理,情况4需要更新障碍集再进行查询. 基于以上4种情况的讨论给出判定规则4. 判定规则4. 情况1中的障碍物发生移动对查询结果不产生影响;情况2中obef和oaft均在Affected_Area内,需要将障碍集更新为O-obef+oaft;情况3中obef在Affected_Area内,需要将障碍集更新为O-obef;情况4中oaft在Affected_Area内,需要将障碍集更新为O+oaft. 基于判定规则4,本节提出的障碍物动态移动情况下的OGRkNN查询算法的主要思想为:首先判断发生移动的障碍物移动前后所在的位置;然后计算受影响区域范围;再根据判定规则4分别对4种情况进行处理;最后得到障碍物移动情况下的OGRkNN查询结果.基于以上讨论,进一步给出障碍物动态移动情况下的查询算法,如算法5所示. 算法5.DYN_MOVE_OGRkNN(Q,P,O,k,obef,oaft). 输入:查询点集Q、数据点集P、原障碍集O、k值、移动前的障碍物obef、移动后的障碍物oaft; 输出:障碍物动态移动时的查询结果集Snew. obef∈O;*移动前的障碍物属于原障碍集O Affected_Area←∅;*受影响区域初始化* Judge_Position(obef);*判断障碍物移动前的位置* Judge_Position(oaft);*判断障碍物移动后的位置* ifobef,oaft∉Affected_Areathen*情况1* SR←STA_OGRkNN(Q,P,O,k); else ifobef,oaft∈Affected_Areathen*情况2)* O′←O-obef; O′←O′+oaft; SR←STA_OGRkNN(Q,P,O′,k); else ifobef∈Affected_Areaandoaft∉Affected_Areathen*情况3* O′←O-obef; SR←STA_OGRkNN(Q,P,O′,k); elseobef∉Affected_Areaandoaft∈Affected_Areathen*情况4* O′←O+oaft; SR←STA_OGRkNN(Q,P,O′,k); endif Snew←SR; returnSnew. 本节通过实验对所提算法进行性能分析.由于已有的研究成果无法直接处理障碍空间中的组反k最近邻查询问题,故我们对文献[15-16]提出的障碍反k最近邻查询算法采用反复调用的方式应用于一组查询点中,形成对比算法.我们将反复调用形成的对比算法分别称作GRkNNobs算法和GORkNN算法.2个对比算法的主要思想为:将已有的针对一个查询对象的障碍反k最近邻查询算法应用到一组查询对象的情况中,也就是采用反复调用的方式对一组对象中的每个对象成员进行障碍反k最近邻查询,所有查询结果的并集就是障碍组反k最近邻查询的结果. 实验平台配置如下:2.0 GHz CPU,4 GB内存,500 GB硬盘,Windows 7操作系统上用Microsoft Visual Studio 2005实现.本文使用的数据集是从美国加利福尼亚州的道路网络中的数据对象集抽取出来的80 000个节点对象和5 000个线段对象.查询点集Q是在节点对象集中随机抽出的n个点的集合.实验测试的指标为运行时间,并取执行100次查询的平均值.实验首先对STA_OGRkNN算法进行测试,分别测试k值、查询点数量、数据点集大小、障碍物个数对于运行时间的影响,然后对动态障碍物环境中的查询方法的3个算法分别进行测试. Fig. 5 Effect of k on runtime图5 k值对CPU时间的影响 如图5所示,首先分析k值对运行时间的影响.实验规模为80 000,查询点的数量为10,障碍物的数量为1 000.图5给出了3个算法的运行时间随着k值变化的对比结果.随着k值的不断变大,算法的CPU时间均呈上升趋势.由于GRkNNobs算法和GORkNN算法需要对每一个查询点计算它的反k最近邻,这样就造成了搜索区域的频繁重叠情况,k值越大,搜索区域重叠的面积越大,从而花费的查询时间越多.本文提出的STA_OGRkNN算法分别对查询点集和数据点集进行了预处理,缩小了查询范围,同时利用Voronoi图的特性进行高效地剪枝和精炼,当k值越大时,该算法的优势越明显. 图6给出了查询点数量对运行时间的影响.实验设定k值为10,数据点集的规模设置为80 000,障碍物的数量为1 000.从图6中可以看出GRkNNobs算法的运行时间上升趋势明显,其次为GORkNN算法,因为这2个算法都需要对每一个查询点计算它的障碍反k最近邻,当查询点数量增长时,算法所用的查询时间也会大幅增长;而STA_OGRkNN算法的查询时间的上升趋势较为平缓,因为算法中有对查询点集的处理过程,所以当查询点数量呈倍数增长时,对算法的性能影响不大. Fig. 6 Effect of query points number on runtime图6 查询点数量对查询时间的影响 Fig. 7 Effect of dataset scale on runtime图7 数据点集规模对CPU时间的影响 图7给出了数据点集规模对算法运行时间的影响.实验设定k值为10,查询点的数量为10,障碍物的数量为1 000.随着数据点集规模的变大,3个算法的运行时间均呈上升趋势.GRkNNobs算法和GORkNN算法在计算一组查询点中每个查询点的障碍反k最近邻时,消耗大量查询时间;而STA_OGRkNN算法首先对查询点集进行优化处理,避免了搜索区域频繁重叠的现象,然后利用Voronoi图的邻接特性在剪枝阶段和精炼阶段有效地过滤掉大量的非候选者,快速地缩小查询范围,故该算法随着数据集的增大所花费的运行时间较少. 接下来分析障碍物的个数对运行时间的影响,实验设定k=10,查询点的数量为10,数据点集的规模为80 000.如图8所示,随着障碍物的数量增加,运行时间越长.GRkNNobs算法和GORkNN算法需要计算每一个查询点的障碍RkNN,这一过程中计算障碍距离的时间花费较大;而STA_OGRkNN算法在剪枝阶段对没有影响的障碍物进行剪枝,故随着障碍物数量的增加,该算法的运行时间增加幅度缓慢. Fig. 8 Effect of obstacal number on runtime图8 障碍物的个数对CPU时间的影响 最后测试动态障碍物环境的OGRkNN查询方法的性能.对GRkNNobs算法和GORkNN算法采取重新调用的方式应用于动态障碍物环境中,形成对比算法.表1反映了本文提出的DYN_ADD_OGRkNN算法与对比算法在障碍物动态增加时的性能对比.实验设定k=10,查询点的数量为10,数据点集的规模为80 000.测试的指标为查询时间,并取执行1 000次查询的平均值.为了方便研究,以每次增加1个障碍物的方式进行测试.如表1所示,当障碍物数量从2 000变成3 000时,DYN_ADD_OGRkNN算法的平均查询时间变化不大,而GRkNNobs算法和GORkNN算法的查询时间几乎呈倍数增长. 表2显示的是当障碍物动态减少时DYN_DEL_OGRkNN算法与对比算法的查询时间比较.对GRkNNobs算法和GORkNN算法采用重新调用的方式应用于障碍物动态减少环境中,此时对比算法的主要思想为:使用减少障碍物之后的新障碍集作为参数,重新执行一遍算法得出结果.如表2所示,GRkNNobs和GORkNN算法的查询时间远远多于DYN_DEL_OGRkNN算法,这是由于2个对比算法只是单纯地重复执行一次;而DYN_DEL_OGRkNN算法会判断减少的障碍物所在的位置,再分别采取不同的方法,这样就避免了很多冗余计算. Table 1 Performance Comparison Between DYN_ADD_OGRkNN and Other Algorithms Table 2 Performance Comparison Between DYN_DEL_OGRkNN and Other Algorithms 表3显示的是当障碍物动态移动时DYN_MOVE_OGRkNN算法与对比算法的平均查询时间比较情况.对GRkNNobs算法和GORkNN算法采用重新调用的方式应用于障碍物动态移动环境中. Table 3 Performance Comparison Between DYN_MOVE_OGRkNN and Other Algorithms 如表3所示,当障碍物发生移动时,GRkNNobs和GORkNN算法的执行时间远多于DYN_MOVE_OGRkNN算法. 本文基于Voronoi图的邻接特性提出了处理障碍空间中组反k最近邻查询的方法,解决了针对静态障碍物环境以及动态障碍物环境下的组反k最近邻查询的问题.给出OGRkNN查询的定义和实现算法.解决该问题的难点在于如何快速准确地获得查询结果,为此提出高效的剪枝规则.在剪枝阶段利用剪枝策略对数据集进行剪枝,过滤掉大量的非候选者,快速地缩小查询范围.在精炼阶段对候选集进行精炼处理提高了算法的准确性.在STA_OGRkNN查询基础上给出障碍物动态增加情况下的OGRkNN查询方法、障碍物动态减少情况下的OGRkNN查询方法以及障碍物动态移动情况下的OGRkNN查询方法.理论研究和实验表明,所提算法具有较好的性能.未来的研究重点主要集中在障碍空间中针对不确定数据的组反k最近邻查询方面.
{∃q∈Q,∃p∈P|q∈OkNN(p,k,P,O)}.2 静态障碍物环境下的OGRkNN查询方法
2.1 剪枝过程
2.2 精炼过程

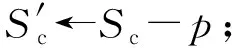
3 动态障碍物环境下的OGRkNN查询方法
3.1 障碍物动态增加情况下的OGRkNN查询方法
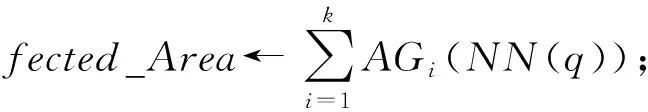
3.2 障碍物动态减少情况下的OGRkNN查询方法
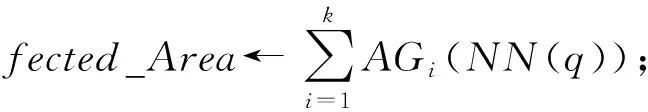
3.3 障碍物动态移动情况下的OGRkNN查询方法
4 实验比较与分析
5 结束语
