内存计算框架局部数据优先拉取策略
2017-11-07修位蓉钱育蓉英昌甜
卞 琛 于 炯 修位蓉 钱育蓉 英昌甜 廖 彬
1(新疆大学信息科学与工程学院 乌鲁木齐 830046)
2 (新疆财经大学统计与信息学院 乌鲁木齐 830012)
近年来,各行业应用数据规模呈爆炸性增长,大数据的4V特性发生不同程度的变化,表现出增速快、增量大、类型多样、结构差异明显等特征[1].传统的并行计算系统由于其计算模型的天生缺陷,在大数据处理过程中存在IO效率低下、并发控制困难、数据处理总体性能较低等诸多问题,难以有效应对实时、即席、交互式分析的复杂业务诉求[2].因此,并行计算系统的性能优化成为大数据研究领域的热点问题,而充分利用内存的低延迟特性改进系统性能成为并行计算新的研究方向[3-4].
通过多年的技术积淀和创新,硬件技术的发展已经突破Dennard Scaling法则.多核技术、异构多核集成技术(CPU与GPU的组合)以及多CPU的并行处理技术相继问世,出现了多核共享内存及多处理器共享内存的新型架构.新兴的存储技术也相继走出实验阶段,开始实现产品化.闪存、相变存储器(PCM)、磁阻式随机存储器(MRAM)和电阻式随机存储器(RRAM),其非易失、随机访问延迟小、并行度高、低功耗、高片载密度等优良特性,为内存计算提供了新的支撑环境.硬件革新催生内存计算技术的发展,内存计算的研究领域也从内存数据管理技术逐渐过渡到基于内存计算的分布式系统.以Berkley研究成果Spark[5-6]为代表的内存计算框架,有效缓解了频繁磁盘IO性能瓶颈,解放了多核CPU配合大容量内存硬件架构的潜在高性能,成为工业界一致认可的高性能并行计算系统.虽然内存计算框架的性能表现相对于传统的并行计算系统提高了数十倍,但与大数据时代的即时应用需求相比,还存在不小的差距.因此,从计算模型的角度研究内存计算框架的性能优化方法具有一定的现实意义.
为进一步优化内存计算框架性能,提高作业执行效率,本文选取开源内存计算框架Spark为研究对象,但并不失一般性,本文的研究成果同样适用于Flink[7],Impala[8],HANA[9],MapReduce[10]等其他类似系统.Spark是继Hadoop之后出现的通用高性能并行计算框架,采用弹性分布式数据集(resilient distributed datasets, RDD)[11]作为数据结构,通过数据集血统(lineage)[11-12]和检查点机制(checkpoint)[13-14]实现系统容错,编程模式则借鉴了函数式编程语言的设计思想,简化了多阶段作业的流程跟踪、任务重新执行和周期性检查点机制的实现.作为新的基于内存计算的分布式系统,Spark参考MapReduce计算模型实现了自己的分布式计算框架;基于数据仓库Hive实现了SQL查询系统Spark SQL[15];参考流式处理系统Storm[16]实现了流式计算框架Spark Streaming[17];并面向机器学习、图计算领域分别设计了算法库MLlib[18]和GraphX[19].
Spark的并行化设计思想源于MapReduce,但与MapReduce不同的是,Spark可以将作业的中间结果保存在内存中,计算过程中不需要再读写HDFS,从而避免了大量磁盘IO操作,提高了作业的执行效率.因此,Spark更适用于需要迭代执行的数据挖掘和机器学习算法.由于能够部署在通用平台上,并且具有可靠性(reliable)、可扩展性(scalable)、高效性(efficient)、低成本(economical)等优点[20],Spark在大数据分布式计算领域得到了广泛运用,并逐渐成为工业界与学术界事实上的大数据并行处理标准.虽然Spark具有众多优点,但与其他并行计算框架一样,宽依赖同步操作导致的作业延时问题仍是不可规避的性能瓶颈.由于Shuffle过程需要等待所有输入数据计算完成,因此高效节点与慢任务节点的强制同步产生大量作业延时和资源浪费.为解决这一问题,本文主要做了4项工作:
1) 对内存计算框架的作业执行机制进行分析,建立资源需求模型和执行效率模型,给出资源占用率、RDD计算代价和作业执行时间的定义,证明了计算资源有效利用的相关原则.
2) 通过分析作业的任务划分策略及调度机制,建立任务分配及调度模型,给出任务并行度、分配效能熵(allocation efficiency entropy, AEE)和节点贡献度(worker contribution degree, WCD)的定义,并证明这些定义与作业执行效率的逻辑关系,为算法设计提供基础模型.
3) 在相关模型定义和证明的基础上,提出局部数据优先拉取策略的优化目标,以此作为算法设计的主要依据.
4) 设计基础数据构建算法和局部数据优先拉取算法(partial data shuffled first algorithm, PDSF),并通过分析算法的基本属性,证明算法帕累托最优.
1 相关工作
内存计算技术研究的基础领域是内存数据管理技术,工业界出现了许多相关产品.Memcached[21]是应用最为广泛的全内存式数据存取系统,该系统通过DHT构建网络拓扑实现数据布局及查询方法,为上层应用提供了高可用的状态存储和可伸缩的应用加速服务,因其具有良好的通用性和鲁棒性,被Facebook,Twitter,YouTube,Reddit等多家世界知名企业使用.与Memcached类似,VMware的Redis[22]也提供了性能卓越的内存存储功能,支持包括字符串、Hash表、链表、集合、有序集合等多种数据类型,提供更加简单且易于使用的API,相比于Memcached,Redis提供了更灵活的缓存失效策略和持久化机制.此外,还有如微软的Hekaton[23]和开源社区的FastDB[24]等内存数据库产品随着需求的发展仍在不断涌现.
近年来,高性能内存计算框架也在不断地充实和发展,除本文的研究对象Spark外,Flink也是较为典型的兼容批处理和流式数据处理的通用数据处理平台,支持增量迭代并具有迭代自动优化功能.Flink具有独立内存管理组件、序列化框架和类型推理引擎,内存管理对JAVA虚拟机的依赖度很低,因此能更有效地掌控和利用内存资源.Cloudera的Impala是基于内存计算技术的新型查询系统,实现嵌套型数据的列存储,有效提高数据查询效率;通过多层查询树结构降低系统的广播开销,提高查询任务的并行度.SAP的HANA已不仅仅是一个内存数据库,更是基于内存计算技术的高性能实时数据处理平台.平台中包含了内存数据库和内存计算引擎,提供完整的内存数据存储和分析计算服务,具有灵活、多用途、数据源无关等诸多优良特性.Apache的Storm更加注重大数据分析的实时性,通过数据在不同算子之间持续流动,达到数据流与计算同步完成的实时性目的,更适用于高响应、低延迟的业务应用场景.此外,Yahoo的S4[25]和微软的TimeStream[26]也是内存计算框架研究领域的重要成员.
随着内存计算框架不断地推陈出新,一些研究成果致力于系统的扩展和完善.文献[27]提出简单而高效的并行流水线编程模型,文献[28]基于BitTorrent实现了内存计算框架的广播通信技术.文献[29]提出关系型大数据分析的标准架构.文献[30]提出图计算的并行化设计方案.文献[31]针对作业中间结果的重复利用问题,设计使用程序分析并定位公共子表达式的复用方法.文献[32]提出集群资源的细粒度共享策略,从而使不同的应用通过相同的API发起细粒度的任务请求.实现资源在不同平台间的动态共享.文献[33-34]设计了统一的内存管理器,将内存存储功能从计算框架中分离出来,使上层计算框架可以更专注计算的本身,以通过更细的分工达到更高的执行效率.文献[35]设计了分布式数据流计算的标准化引擎.文献[36]实现了高性能的SQL查询系统.文献[37-38]提出了差分数据流和及时响应应用的并行计算方法.文献[39]设计了大数据交互式分析的联合聚合通用模型.文献[40]实现了内存计算集群的隐私消息通信系统.文献[41]提出了内存计算框架的分布式调度算法,使多个应用可以非集中化地在同一集群上排队工作,同时提供数据本地性、低延迟和公平性,极大地提升系统的可扩展性.
另外一些研究成果关注内存计算框架的性能优化.文献[42]提出充分利用数据访问时间和空间局部性,设计了提高本地性的数据访问策略.文献[43]通过分析任务并行度对缓存有效性的影响,设计适应于内存计算的协调缓存算法.文献[44]通过监测作业的计算开销,发现reduce任务的并行度对类MapReduce系统的性能有较大影响,由此设计了适应资源状况的任务调度算法.文献[45-46]针对慢任务节点问题提出了不同的优化方法,保障作业执行的持续性.文献[47]通过批处理事务和确定性执行2种策略,使系统拥有更好的扩展性和可靠性.文献[48]以推测worker响应时间的方式,将作业划分为不同的区块,采用延迟隐藏技术提高紧密同步型应用程序的执行效率.文献[49]提出了工作节点的通信成本边界模型,并通过调整边界阈值的方法找到任务并行度与通信成本的最佳平衡点.
本文与上述研究成果的不同之处在于从计算模型的基本原理入手,以提高作业执行效率和改进系统性能为目的,建立了内存计算框架的局部数据优先拉取策略.通过分析作业的执行过程,建立了资源需求模型和执行效率模型.提出了资源占用率、RDD计算代价的定义,并证明了资源有效利用的相关原则.建立任务分配及调度模型,提出了分配效能熵、节点贡献度的定义,并证明了上述2个定义与作业执行效率的逻辑关系.根据局部数据优先拉取策略的问题定义进行求解,提出了基础数据构建算法和局部优先拉取算法,通过任务的适度倾斜分配,充分利用高效工作节点的计算能力;通过局部数据优先拉取,缓解宽依赖同步的节点空闲问题,提高工作节点的参与度,从而从整体上优化作业执行效率,改进系统性能.相比于已有的研究工作,局部数据优先拉取策略更适宜于内存计算框架的性能优化,并具有较高的普适性和易用性.
2 问题的建模与分析
本节首先分析作业的并行执行机制,建立资源需求模型、执行效率模型和任务分配及调度模型,然后提出局部数据优先拉取策略的问题定义,为第3节基础数据构建算法和局部数据优先拉取算法提供理论基础.
2.1 作业执行机制
Spark的作业执行采用了延时调度机制,当用户对一个RDD执行Action(如count,collect)操作时,调度器会根据RDD的血统(lineage)来构建一个由Stage组成的有向无环图(DAG),然后为工作节点分配任务执行程序.Spark任务DAG的典型示例如图1所示,其中实线圆角方框表示RDD,矩形表示分区,虚线框为Stage.Action操作的执行将会以宽依赖分区来构建各个Stage,每个Stage都包含尽可能多的连续的窄依赖,Stage内部的窄依赖前后连接构成流水线.而Stage之间的分界则是宽依赖的Shuffle操作,各Stage同步顺序执行,直到最终得出目标RDD.各工作节点的任务分配根据数据存储本地性来确定,若一个任务需要处理的某个分区刚好存储在某个节点的内存中,则该任务会分配给这个节点;否则,将任务分配给具有最佳位置的工作节点.
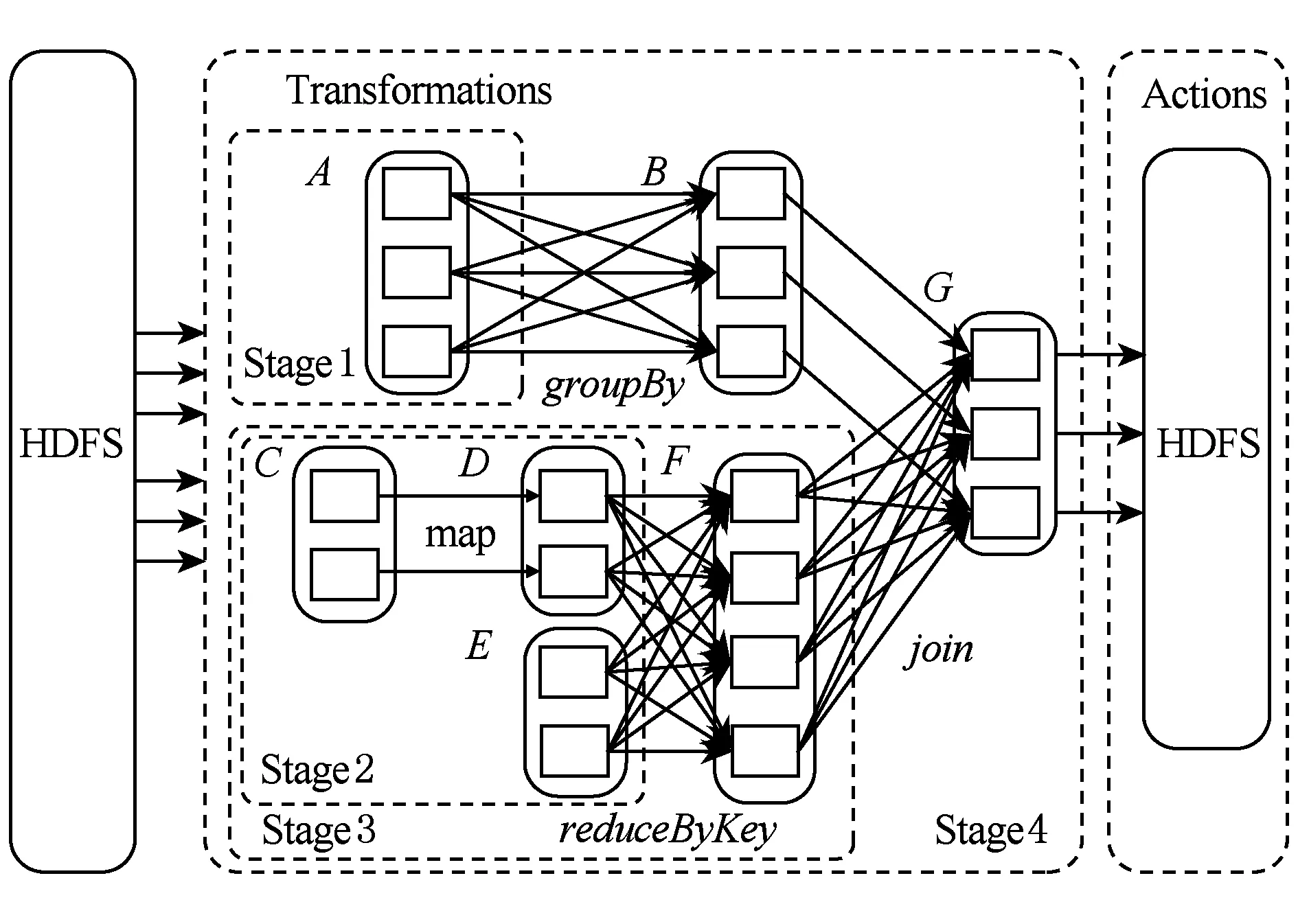
Fig. 1 Directed acyclic graph of Spark job图1 Spark任务的有向无环图
2.2 资源需求模型
在并行计算集群中,资源池由一系列工作节点构成,定义工作节点集合W={1,2,…,m},每个工作节点包含多种计算资源,如CPU、内存、磁盘等.定义资源种类集合R={1,2,…,k},记r∈R.对于每个工作节点w∈W,记cw=(cw1,cw2,…,cwk)为该工作节点的可用资源向量,这里cwr为工作节点w上可用资源r的数量.不失一般性,对于集群每一类资源r进行正则化,即:
(1)
记workload={1,2,…,h}为Spark框架一个时间段同时运行的作业.对于每个作业i,记di=(di1,di2,…,dik)T为其在集群中的资源需求向量,这里dir为作业i对资源r需求量占集群资源r总量的比例,由于每个作业的资源需求都是正向的,即:
dir>0,i∈workload,r∈R,
(2)
那么所有作业的资源需求为k×n的矩阵,即:
(3)
并行计算框架要求作业执行前首先提供资源需求表,用于描述的是每个工作节点需要占用的各种资源量,如2个CPU核心、16 GB内存.并行计算框架选择空闲资源符合资源需求表的工作节点执行作业,记Extors={1,2,…,n}为执行作业i的工作节点集合,则Extors⊆W,记Aiw=(Aiw1,Aiw2,…,Aiwr)为作业i在工作节点w上的资源分配向量,原则上每个执行任务的工作节点都严格按照资源需求表分配资源,则有:
(4)
定义1. 资源占用率.用于衡量作业使用的资源量占集群资源总量的比例.为使衡量标准更加精确,度量过程以Tcycle为1个周期,记Tjobi为作业i的执行时间.由于已对集群资源进行了正则化,因此对于作业占用的任意类型资源r,其资源占用率可表示:
(5)
定理1. 资源有效利用原则.在不影响作业执行效率的前提下,单位时间资源占用率越小,则集群任务的并发度越高,集群资源的利用率也越高.
证明. 设作业x调度时集群的空闲资源向量为B=(b1,b2,…,br),仅当所有类型资源的需求量均小于空闲资源量,即dxr (6) 若当前周期内正在执行的作业集合为workload={1,2,…,h},根据定义1,任意类型的资源空闲量可表示为 (7) 由于整个集群资源总量恒定,Uir越小,则br越大,dxr 证毕. 根据Spark的延迟调度机制,作业在执行到Action操作时,生成由多个RDD组成的DAG,首先以宽依赖分界划分Stage,每个Stage包括多个RDD,每个RDD又被划分成多个分区工作节点并行计算,因此,对于每一个作业,记其Stage集合为stages={stage1,stage2,…,stagei},记每个Satge的RDD集合为stagei={RDDi1,RDDi2,…,RDDij},这里RDDij表示第i个Stage中第j个RDD,对于每个RDD,记其分区集合为RDDij={Pij1,Pij2,…,Pijk},其中,Pijk表示RDDij中的第k个分区. 定义2. RDD计算代价.Spark任务中,分区是以一个或多个父节点为输入数据计算生成,设Parentsijk为分区Pijk的父节点集合.分区的计算首先要读取所有的输入数据,然后根据闭包和操作类型进行计算.因此分区Pijk的计算代价为数据读取代价与数据处理代价之和,评估过程以分区计算时间作为衡量计算代价的指标,即: TPijk=read(Parentsijk)+proc(Parentsijk). (8) RDD的所有分区由集群工作节点并行计算生成,因此其计算代价为所有分区计算代价的最大值,即: (9) 定义3. 作业执行时间.如图1所示,Spark以宽依赖为分界点,将作业划分为多个Stage执行,那么每个Stage包含1个宽依赖RDD或多条流水线(每条流水线包括多个RDD的不同分区).设stagei共有m个RDD,除末尾的宽依赖RDDim外,其余RDD划分为x条流水线,单条流水线的分区集合为pipeix={Pi1x,Pi2x,…,Pijx},那么单条流水线的执行时间可表示为 (10) 对于stagei,记其流水线集合为Pipesi={pipei1,pipei2,…,pipeix},那么stagei的执行时间应为各流水线执行时间最大值与RDDim计算时长之和,即: (11) 若Spark将作业划分为n个Stage,各Stage同步顺序执行,因此作业的执行时间为 (12) 并行计算任务调度时,将作业按照分区划分成任务,一个分区对应一个计算任务.在实际的任务分配过程中,数据本地性是分配的首要因素,因此当前的分区计算任务会优先分配到其前导分区所在的工作节点.依次类推,系统会将到达目标RDD的一条路径分配给一个工作节点,因此图1中Stage3的执行将产生如图2中所示的任务分配方案. Fig. 2 Task allocation of traditional Spark图2 传统Spark的任务分配 (13) 那么工作节点w在整个作业上的任务分配可以表示为 ATw=AT1w∪AT2w∪…∪ATiw. (14) 任务分配满足3个特性:1)任意工作节点上的任务分配与其他节点的分配没有交集;2)对于工作节点w的任务分配ATw,其相同Stage中的相邻任务必为前导后续关系;3)各工作节点的任务分配相对平均,满足负载均衡. 定义5. 分配效能熵.用于衡量任务分配与工作节点计算能力的适应度.记TW为作业的总工作量,对于参与作业计算的工作节点集合Extors={1,2,…,n},CPS={cp1,cp2,…,cpn}表示Extors中每个工作节点的计算能力.那么所有节点任务执行时间的均值可定义为 (15) 在不考虑宽依赖同步问题的前提下,对于任意的工作节点w,其任务分配ATw的执行时间可表示为 (16) 因此工作节点任务执行时间的方差可表示为 (17) 那么节点的分配效能熵可表示为 (18) 定理2. 对于所有参与计算的工作节点,其分配效能熵越大,作业的执行时间越短,计算效率越高. 证明. 基于定义3,从任务分配的角度来看,作业的执行时间也可表示为 (19) 根据式(18),节点的分配效能熵与方差成反比,因此熵值越大,方差越小,表示节点任务完成时间越趋近均值,因此当所有工作节点的分配效能熵取最大值时,作业的执行时间最短,执行效率最高. 证毕. 定义6. 任务并行度.用于衡量同一时间并发的任务数.在内存计算框架中,系统通过文件的Block数量自动推断并行度,称为默认并行度.这一参数表示用户无介入条件下执行作业的任务并发数,因此默认并行度与单个Stage内的流水线数量相同.在实际运行环境中,默认并行度仅是个理论参考值,因为划分的多个任务能否并发,还要依赖于工作节点的数量以及每个节点分配的CPU核心数.根据2.2节资源需求模型,记作业调度时符合资源需求表的工作节点数为n,每个工作节点分配的CPU核心数为g,那么硬件环境所能支持的最大并发数为n×g,称为物理并行度.设输入数据的Block数量为l,那么对于默认并行度l和物理并行度n×g,应当遵循最小值优先,因此实际的任务并行度可以表示为 dpi=min{l,n×g}. (20) 定义7. 节点空闲时间.用于表示工作节点因任务分配不均匀导致的空闲时间段.根据定义6,当默认并行度大于物理并行度,即l>n×g时,表示Stage内的流水线数大于任务并行度,那么工作节点需要被多轮分配,任务分配轮数可表示为 (21) 其中,ceiling函数表示取大于等于参数值的最小整数.通过式(21)可以看出,当l为n×g整数倍时,参与计算的每个工作节点在每轮分配中都能得到任务,而l与n×g相除余数不为0时,必有部分工作节点在最后一轮分配时空闲,轮空的工作节点数可表示为 Countbye=n×g-mod(l,(n×g)), (22) (23) 定义8. 节点停等时间.根据定义4描述的任务分配过程,每个参与计算的工作节点至少分配一条流水线和一个宽依赖RDD分区,流水线各工作节点并行执行,进度各有快慢.而在计算宽依赖RDD时,由于其每个分区的计算需要依赖父RDD的所有分区,而父RDD不同分区是由不同工作节点流水线中计算的.因此,在宽依赖RDD计算开始前,所有参与计算的工作节点需要先同步,即等待所有父分区计算完成后统一开始宽依赖RDD的计算.计算效率较高的工作节点执行到宽依赖RDD,需要等待慢节点的计算结果.记执行作业的工作节点集合Extors={1,2,…,n}已按分配流水线的完成顺序排列,相邻工作节点流水线完成时间差分别为T1,T2,…,Tn-1,那么对于工作节点w,其停等时间可表示为 (24) 需要说明的是,在2.2节资源需求模型的描述中,只有符合资源需求表的工作节点才能参与作业执行,理论上各工作节点可用的资源量一致,流水线执行效率也应当基本相同.但资源需求表仅对不同类型资源作模糊量化,例如CPU核心数、内存容量等(参见2.2节示例),异构云环境下工作节点的CPU及内存型号多种多样,参数也各有不同,即使都符合资源需求表,不同工作节点的计算能力也有差异.另外,由于输入数据locality的限制,工作节点的网络传输能力也会影响流水线执行效率. 定义9. 节点贡献度.用于衡量工作节点在作业执行过程中实际参与计算的比例.值越大则参与度越高,说明工作节点计算能力被利用的越充分.根据前面的定义,工作节点在完成作业过程中,存在空闲时间和停等时间.因此对于工作节点w,其贡献度应为实际计算时间与作业执行时间和比值,表示如下: (25) 节点贡献度精确刻画了工作节点计算能力的发挥程度,在作业计算量和工作节点计算能力稳定的前提下,贡献度越大,工作节点计算能力的利用度越高. 定理3. 对于所有参与计算的工作节点,其贡献度越大,则节点任务执行时间的均值越小,作业执行效率的优化度越高. (26) 由于作业的总工作量TW为定值,节点的原始计算能力cpw也为定值,那么当节点的贡献度Qw取最大值时,均值E为最小值,作业执行效率具有最高的优化度. 证毕. 2.2~2.4节已经对作业资源需求、任务执行效率和任务调度过程作了比较详细的阐述,基于这些定义,局部优先拉取任务调度算法可形式化为 object min(Tjob), (27) s.t. (28) 目标是作业执行效率最大化,约束条件是资源分配量符合资源需求表,即在资源稳定的前提下寻求作业执行效率最大化的目标.然而这一目标定义的实际操作性不强,度量方法也过于粗糙.因此,根据分配效能熵和节点贡献度的定义,可将上述问题等价于: object (29) (30) s.t. (31) 目标是最大化分配效能熵和节点贡献度,约束条件同上.很显然,在任务分配中,根据节点计算能力作适度倾斜,可以使工作节点得到最大化的分配效能熵.通过削减工作节点的空闲时间和停等时间,能够提高节点贡献度,最终达到作业执行效率的优化目标. 本节基于模型的相关定义及定理证明,首先构建算法所需的基础数据;然后提出局部数据优先拉取算法,并对算法的基本属性进行分析和证明;最后对算法附加开销进行评估. 局部数据优先拉取算法需要构建的基础数据如下: 1) 空闲节点池freePool.用于存放已完成任务并处于等待状态的工作节点.无论是流水线还是局部拉取任务(参见3.2节),工作节点只要计算完毕就进入freePool,因此freePool在作业执行过程中不断变化. 2) 输入分区表inputParts.用于保存工作节点所执行任务的计算结果.工作节点在输入分区表中的记录数与其分配的流水线数量相同,每条记录只保存流水线所在路径最近一次的计算结果.需要说明的是,计算结果加入inputParts的过程不存在数据复制,inputParts中的记录只保存引用,实际数据仍分散在各个工作节点上. 3) 分区状态表partsState.与输入分区表相对应,用于标识计算结果是由哪些父分区计算生成.标识的方法采用追加式,即局部拉取使用了哪些父分区,就在记录中追加这些分区的编号. 基础数据为局部数据优先拉取算法的各步骤提供数据和计算支持.空闲节点池提供局部拉取任务的节点候选者,输入分区表为局部拉取任务提供输入数据,而分区状态表一方面避免重复计算,另一方面为局部拉取任务提供分配依据. 算法1. 基础数据构建算法. 输入:工作节点列表nodes; 输出:freePool,inputParts,partsState. ① fori=0 tonodes.Length-1 do ② ifnodes[i].Finish=true then ③freePool.add(nodes[i]); ④ ifinputParts.contains(nodes[i]) then ⑤inputParts.replace(nodes[i].LastPt); ⑥ else ⑦inputParts.add(nodes[i].LastPt); ⑧ end if ⑨partsState.update(); ⑩ end if 本节求解2.5节所定义的带约束条件的最优化问题.算法的主要思想是削减宽依赖同步产生的节点空闲,充分发挥高效工作节点的计算能力,弥补慢节点导致的作业延时,从而提高作业执行效率.本文提出基于启发式算法的局部优先拉取调度算法,主要有4个步骤: 1) NodeGroup划分.首轮划分中,先后2个进入空闲节点池freePool的工作节点划分为一个NodeGroup.生成一个NodeGroup表示输入分区集合至少包含2个分区,因此可以开始计算基于这2个分区的Shuffle结果.当NodeGroup的局部拉取任务完成后,工作节点再次加入空闲节点池,等待下一轮NodeGroup划分,再次划分至少需要加入1个新的工作节点或其他NodeGroup.因为同一个NodeGroup的工作节点可能再次划分到一个新的NodeGroup中,而这2个节点的局部拉取任务已完成,仅有这2个节点的NodeGroup属无效划分. 2) 中断令牌轮转.空闲节点池有1个中断令牌,在生成的NodeGroup之间传递,中断令牌总由最近生成的NodeGroup持有.当最后一个工作节点进入空闲节点池时,若没有组成NodeGroup(空闲节点池中只有1个节点),则获得中断令牌的NodeGroup终止局部拉取任务并回溯状态,与最后一个工作节点合并为一个新的NodeGroup,开始3方的局部拉取任务. 3) 生成局部拉取任务.每个任务需要输入数据、操作和闭包3个要素,操作和闭包直接从宽依赖RDD继承(所有局部拉取任务的操作和闭包与宽依赖RDD相同).输入数据则需要根据partsState中的记录确定.对于NodeGroup中工作节点,查询分区状态表partsState中的相应记录,将这些记录取并集记为sumParts,那么将sumParts与工作节点记录取差集即为该节点需要的输入数据. 4) 快慢节点任务交换.从第2轮划分开始,每个NodeGroup生成后,NodeGroup内的工作节点进行任务交换,交换的依据为最大均量原则,即最快的节点与最慢的节点互换任务,其余工作节点的任务保持不变.任务交换完成后,每个工作节点根据自己的新任务从inputParts中读取输入数据执行计算. 局部数据优先拉取算法的操作过程如算法2所示: 算法2. 局部数据优先拉取算法. 输入:空闲节点池freePool、分区表inputParts. ① iffreePool.Count>1 then Fig. 3 Task allocation of PDSF图3 局部数据优先拉取策略的任务分配 ② iffreePool.checkNodeGroup()=true then ③waitforOtherNode(); ④ else ⑤ng=freePool.createNodeGroup(); ⑥freePool.clear(); ⑦ng.getToken(); ⑧ng.exchangeTask(); ⑨ng.doPartialTask(); ⑩ end if 在局部数据优先拉取算法中,工作节点不需要完全同步,只要宽依赖RDD有2个父分区计算完成,局部拉取任务即开始分配执行.采用PDSF的算法,图2给出的作业执行时序改变为图3所示的状态. 在传统的Spark框架中,作业执行到宽依赖RDD要进行强制同步,即所有输入数据必须计算完成且划分到不同的Bucket中才启动宽依赖RDD的计算任务,从输入分区的Bucket拉取数据并执行后续计算.而从图3中可以看出,当分区E1,E2数据划分完毕后,PDSF即启动局部拉取任务PF1和PF2,其中PF1拉取E1,E2中Bucket3中的数据计算局部结果,PF2拉取E1,E2中Bucket4中的数据计算局部结果.若PF1,PF2完成后,任务D2也完成数据划分,则Worker2加入NodeGroup,开始3方局部拉取任务.此时Worker3与Worker2交换任务(PF1为第1个完成的局部拉取任务),Worker2拉取PF1的局部结果,与本地保存的Bucket3的计算结果合并,生成新的局部结果.Worker3则拉取D2,E1,E2中的Bucket2,计算局部结果.Worker4的任务不变,拉取D2的Bucket4,计算局部结果.当3方局部拉取任务完成后,若任务D1也完成数据划分,则执行最后一轮局部拉取任务,Worker4与Worker1交换任务(3方局部拉取任务中Worker4率先完成),Worker1拉取PF5的局部结果,与本地保存的Bucket4的计算结果合并,生成最终的分区F4,Worker4拉取D1,D2,E1,E2中的Bucket1,计算最终分区F1,Worker2和Worker3的任务不变,分别生成最终分区F3和F2. 在异构集群环境中,只有缩减慢节点的任务执行时间才能提高作业的执行效率,下面通过慢节点Worker1任务执行具体过程来分析算法的整体效率.在传统Spark实现中,Worker1计算分区F1需要拉取3个Bucket的数据,计算4个Bucket的数据才能得到结果(其中1个Bucket本地存放).通过PDSF,Worker1仅需拉取3个Bucket的数据,计算1个Bucket的数据即可得到结果.另一方面,Worker4领取Worker1的任务后,需要拉取3个Bucket的数据,计算4个Bucket的数据,与传统Spark实现相比,拉取数据量和计算数据量没有发生变化,任务交换不会带来更大的作业延时.需要说明的是,在评估数据拉取量和计算量时都以Bucket为单位,因此Bucket的数据量要相对平均,算法实现中采用了文献[50]的研究成果,保障Bucket划分的均衡性.从上述分析结果来看,慢节点的计算数据量显著减少,而通过网络拉取的数据量则没有变化,优化效果并不明显.实际上,Spark划分Bucket的过程会将数据Spill到磁盘文件中,因此从Bucket中拉取数据的时长为磁盘IO时长与网络传输时长的总和.而Worker1拉取的3个Bucket的数据实为局部拉取任务的计算结果,这些结果存储在内存中,拉取过程仅有网络延时没有磁盘IO,因此慢节点的数据拉取效率也有显著提高.此外,由于传统Spark在同步完成后才启动宽依赖RDD的数据拉取和计算工作,因此PDSF前几轮的局部数据拉取所附加的网络开销处于网络空闲期内,对作业执行效率并无影响. 值得注意的是,图3表示局部数据优先拉取算法的理想状况,即每个已划分NodeGroup的局部拉取任务都能够完成,不存在使用中断令牌回溯状态的情况,在实际应用中很难达到这种理想状态.但对于PDSF算法,只要正常完成一次局部拉取任务,作业执行效率就能得到一定程度的优化,即便一次都没有完成,也不会对作业执行效率产生负面影响,因为中断令牌策略能够保障最慢工作节点的计算连续性. 局部数据优先拉取算法符合以下原则:节点空闲时间清零原则、节点停等时间最小化原则、适度倾斜任务分配原则和数据本地性恒定原则. 定理4. 节点空闲时间清零原则. 证明. 根据定义7,在默认并行度大于物理并行度的情况下,流水线的最后一轮的分配很可能不均匀,因此轮空节点存在空闲时间.通过算法2描述,轮空节点加入空闲节点池freePool,由于最后一轮分配时,之前分配的流水线都已完成计算,inputParts已包含多个输入分区,partsState中也存在多条记录,那么所有轮空节点生成NodeGroup,根据partsState中的相应记录到inputParts中获取输入数据,执行局部优先拉取任务,因此局部数据优先拉取算法无节点空闲时间. 证毕. 定理5. 节点停等时间最小化原则. 证明. 设执行作业的工作节点集合Extors={1,2,…,n}已按其分配流水线的完成顺序排列,相邻工作节点流水线完成时间差分别为T1,T2,…,Tn-1,那么根据定义8,对于工作节点w,其停等时间为 极限情况下,最后一个节点进入freePool时,工作节点x一个局部拉取任务都没有完成,且被回滚与最后一个节点重组NodeGroup,此时x的停等时间与传统调度算法的停等时间一致,因此有: 通过NodeGroup的划分规则可知,每个节点至多再等待一个节点即开始局部拉取任务,节点具有最小的同步开销,编号越小的工作节点停等时间的优化度越高,因此局部数据拉取算法符合节点停等时间最小化原则. 证毕. 定理6. 适度倾斜任务分配原则. 证明. 设当前NodeGroup的工作节点已按照计算能力从大到小排列,所有节点在inputParts中的记录集合为{P1,P2,…,Pm}.根据NodeGroup的划分规则,工作节点x已完成多轮局部拉取任务,而工作节点y还没有执行局部拉取任务.那么对于工作节点x,在partsState中的记录格式为“1,2,…,m-1”,表示x已完成前m-1个分区的数据局部拉取;而对于工作节点y,在partsState中的记录格式为“m”,表示y未执行过局部拉取任务. 在任务交换前,工作节点x将要执行的局部拉取任务可定义为 工作节点y将要执行的局部拉取任务可定义为 证毕. 定理7. 数据本地性恒定原则. 证明. PDSF算法中,每个NodeGroup生成后,快慢节点交换任务,因此节点计算所需的输入数据发生变化.但对于NodeGroup中的慢节点,无论是否发生任务交换,慢节点本地内存中都只包含输入数据的一个分区,计算要用到的其他分区都需要从别的节点获取,因此慢节点的数据本地性不因任务交换而改变,作业的执行效率不受影响. 证毕. 通过上述4个原则的证明可以看出,局部数据优先拉取算法满足2.5节定义的优化目标,在作业宽依赖同步问题不可归避的条件下,算法符合帕累托最优. 假设系统当前执行的作业共包含μ个宽依赖操作,宽依赖RDD分区数为f,根据局部数据优先拉取算法的执行过程,每2个分区计算完成可以开始1次局部拉取任务,因此至多分配μ×(f-1)个局部拉取任务,所以局部数据优先拉取算法的时间复杂度为O(μ(f-1)),在用户请求的作业数量较大时,可以将局部数据拉取任务的分配过程交由多个空闲节点计算,当分配给k个工作节点计算时,只需要做一个简单的同步操作,可以将时间复杂度降低为O(μ(f-1)k). 算法的存储开销包括空闲节点池freePool、输入分区表inputParts和分区状态表partsState占用的存储空间.其中,freePool用于保存空闲节点编号,每个工作节点的编号为4 B的GUID,即使在上千节点的大型集群上,freePool最多占4 MB左右的存储空间,更何况由于局部拉取任务的分配,节点编号会不断地移进移出,同一时间点上的记录总数要远远小于集群节点数.对于inputParts和partsState,保存的记录数与宽依赖节点的分区数相等,每条记录仅仅保存分区引用和编号,可以忽略不计.另外,算法中划分的NodeGroup只是一个逻辑概念,分配一次局部拉取任务产生一个NodeGroup,但NodeGroup信息不需要持久化,因此不占用额外的存储空间. 算法的通信开销主要是freePool,inputParts,partsState中的记录更新.根据算法存储开销的分析,3张表仅存储简单类型和引用,每条记录的数据量很少,记录更新过程仅相当于一次平衡心跳,而且记录更新工作是由空闲节点完成,因此算法并无附加通信开销. 由上述分析可以看出,算法具有较低的时间复杂度,无附加通信开销,仅在Master上产生极微量的存储开销.因此,PDSF算法完全适应任务密集的并行计算集群. Fig. 4 Performance of PDSF图4 局部数据优先拉取策略的整体性能 实验环境用1台服务器和8个工作节点建立计算集群,服务器作为Spark的Master和Hadoop的NameNode.为体现工作节点的计算能力不同,8个工作节点由1个高效节点、6个普通节点和1个慢任务节点组成,其中普通节点的配置如表1所示,高效节点配备4颗CPU阵列、64 GB内存和4个千兆网卡,而慢任务节点仅有单核CPU、2 GB内存和1个百兆网卡.任务执行时间的数据来源于Spark的控制台,而内存使用状况的监控由nmon完成.在Spark框架下,任务的执行速度很快,通常会在几秒内完成,这并不利于准确监控任务执行时间和资源使用状况,因此实验选择在小型集群上进行测试,以便观察到作业执行的更多细节. 实验数据选取SNAP[51]提供的6个标准数据集,均为有向图,如表2所示.作业选用PageRank算法,PageRank的每轮迭代都包含join和reduceByKey共2个宽依赖操作,因此更有利于验证算法的有效性. Table 1 Configuration Parameters of Worker表1 Worker节点配置参数 Table 2 Information of Datasets表2 测试数据集列表 根据2.4节定理2和定理3,局部数据优先拉取算法能够有效提高作业执行效率.实验选择了4个不同大小的数据集测试算法性能,验证理论模型的正确性.实验结果如图4所示: 由图4可以看出,对于每一个数据集,传统Spark与PDSF算法的作业执行时间都随迭代次数的增加而增长.PDSF算法的作业执行时间明显小于传统Spark,从而证明PDSF算法对Spark框架的性能具有优化效果.从作业执行的总体趋势来看,迭代次数越多,作业执行时间的优化效果越明显.但从不同迭代次数的优化效果来看,作业执行时间的缩减比例并未随迭代次数增加呈线性增长.一方面,在不同的时间点,工作节点的计算能力表现不同,某个系统服务运行或突发的网络访问,都会对节点的计算能力产生影响;另一方面,在PDSF算法中,作业执行时间的优化率取决于局部拉取任务的完成情况,中断回溯的次数越少,优化效果越明显. 从图4整体的对比结果来看,在不同数据集环境下,随着迭代次数的增加,传统Spark任务执行时间的上升趋势较为明显,PDSF算法由于局部拉取任务的优先执行,提前进行部分数据的Shuffle操作,因此任务执行时间的上升趋势相对缓和.由此可以看出,传统Spark对宽依赖操作的敏感度很高;而对于PDSF,作业的宽依赖操作越多,局部数据拉取任务的调度概率越大,而局部数据拉取任务的完成度越高,作业执行的加速效应也越明显. Fig. 5 CPU utilization of high performance executor图5 高效节点的CPU利用率 根据3.3节定理4和定理5,通过局部数据优先拉取,能够有效减少节点空闲时间和停等时间,提高高效节点的贡献度.本节实验用于验证PDSF算法对节点贡献度的影响,实验选取节点和连接数差异较大的2个数据集,迭代计算10次.采用nmon监控作业执行过程中各类型资源使用细节,通过观察发现,内存和网络的利用率对节点贡献度的体现能力较差,而CPU利用率最能真实反映节点参与计算的具体细节,因此在作业执行过程中重点监测高效节点的CPU使用情况,实验结果如图5所示,图5(a)(b)分别为数据集web-BerkStan和Higgs-Twitter的测试结果. 由实验结果可以看出,由于PDSF算法能够提高作业执行效率,因此PDSF的作业执行时间明显小于传统Spark.CPU占用方面,传统Spark和PDSF算法在2次测试中都具有较高的CPU占用率,这是因为Spark计算框架充分发挥了内存低延迟特性,CPU计算能力得到了更有效地发挥.比较CPU占用率变化曲线,传统Spark作业执行过程中,CPU占用率的波动幅度较大,特别是几个波谷处的下降幅度明显.由于实验集群中高效节点与慢节点的计算能力差异较大,高效节点在每次宽依赖操作时,都要强制同步等待其他节点,此时CPU处于相对空闲的状态,因此从整个作业执行过程来看,CPU占用率的变化幅度较大,空闲时段也频繁出现.而对于PDSF算法,CPU占用率的整体幅度较为平稳,无明显的空闲时段,因为PDSF进行适度倾斜的任务分配,只要有2个节点流水线计算完成即开始局部拉取任务,从而最小化节点空闲时间和停等时间,有效提高节点在作业执行过程中的参与度,使CPU始终保持较为稳定的高占用状态. 虽然PDSF算法稳定的CPU占用率符合预期,但对作业执行实际的优化效果有限.在PDSF算法中,为了保障作业执行时间不高于传统Spark,慢任务节点不能出现停等时间或空闲时间,一旦慢任务节点流水线计算完成,若空闲节点池中没有节点与其形成新的NodeGroup,则持有中断令牌的NodeGroup停止局部拉取任务,并与慢任务节点合并成新的NodeGroup执行下一轮任务.因此稳定的CPU高占用率也并非都属于有效计算,也包括一些未完成的局部拉取任务被中断回溯的过程. 为了验证PDSF算法在多个不同类型作业并发环境下的性能表现,实验将Spark官方示例中的多个作业组成工作集,其中包括最小二乘法、逻辑回归、K-means聚类、SortByKey等多种作业类型.作业的资源需求则在符合集群既有条件下随机变化,工作集中的作业按FIFO方式组成队列,只要集群空闲资源符合作业需求,即开始执行作业.实验监测了不同时间点的作业完成总数,对于在监测时间点未完成的作业,则用已执行时间与作业执行总时间的比值计算完成比例,实验结果如图6所示: Fig. 6 Performance comparison in multi task concurrent environments图6 多任务并发环境的性能对比 由图6可以看出,在所有的监测点,PDSF算法的作业完成数都大于传统Spark,从而证明了PDSF算法在多作业并发环境下仍具有良好的优化效果.通过观察所有监测点数据发现,不同监测点作业完成量的提高程度各不相同,这是因为不同时间段内执行的作业类型不同,不同类型作业宽依赖操作个数不同,因此在作业类型随机变化条件下,PDSF算法的优化效果无明显规律. 此外,通过定理1的证明,作业执行时间的减少能够提高资源的有效利用率,从任务调度的角度来看,同一时间段内调度的作业数量越多,资源的有效利用率越高,因此在多作业并发实验中提取了作业调度概率的累积分布,用于反映资源有效利用率的变化.记p(r)为资源需求为r的作业被调度的概率,记F(r)=P(p(r)=1)为资源需求为r的所有作业被调度的累积分布函数,图7显示了传统Spark与PDSF算法作业调度概率的累积分布.从图7中可以看出,PDSF算法具有良好的效果,作业调度概率的分布趋势明显优于传统Spark.因此,PDSF算法在优化作业执行效率的同时,提高了集群资源的有效利用率. Fig. 7 CDF of job scheduled probability图7 作业调度概率累积分布 本文针对内存计算框架宽依赖同步操作的作业延时问题,对内存计算框架的作业执行机制进行深入分析,建立资源需求模型和执行效率模型,给出了资源占用率、RDD计算代价和作业执行时间的定义,证明了计算资源有效利用原则.通过分析作业的任务划分策略及调度机制,建立了任务分配及调度模型,给出了任务并行度、分配效能熵和节点贡献度的定义,并证明这些定义与作业执行效率的逻辑关系,为算法设计提供基础模型.在相关模型定义和证明的基础上,提出了局部数据优先拉取策略的优化目标,并对评估指标加以细化,以此作为算法设计的主要依据.根据模型和优化目标,设计了基础数据构建算法和局部数据优先拉取算法,通过分析算法的基本属性,证明了算法的帕累托最优性.最后,通过不同的实验证明算法的有效性,实验结果表明,PDSF算法提高了内存计算框架作业执行效率,并使集群资源得到有效利用. 工作主要集中在4个方面: 1) 异构集群多作业并发环境下,研究工作节点计算能力利用率最大化的任务分配策略. 2) 分析内存计算框架不同类型操作资源需求的一般规律,设计适应作业类型的资源分配和任务调度策略. 3) 随着GPU计算技术的发展,利用GPU提高作业执行效率变得可行.通过构建CPU+GPU的多核集成协同计算架构提升系统性能是今后的一个研究方向. 4) 高速缓存也是影响内存计算框架性能的重要因素,针对高速缓存低命中率引发的伪流水线问题,设计高速缓存级别的优化策略是今后研究的另一个方向.2.3 执行效率模型
2.4 任务分配及调度模型
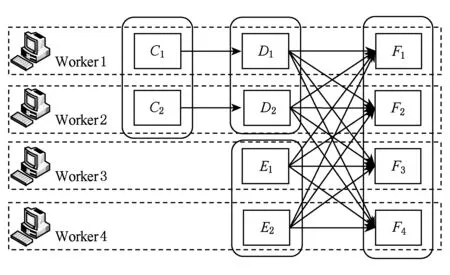
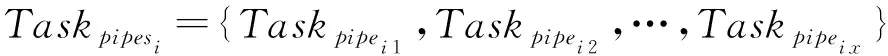
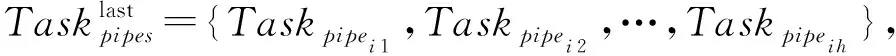
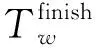
2.5 局部数据优先拉取策略问题定义
3 局部数据优先拉取策略
3.1 构建基础数据
3.2 局部数据优先拉取算法
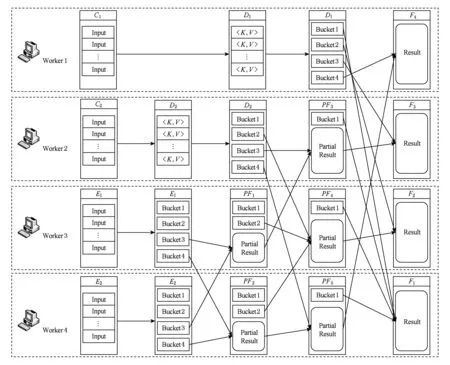
3.3 算法的相关原则
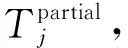
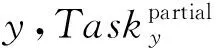
3.4 算法开销分析
4 实验与评价
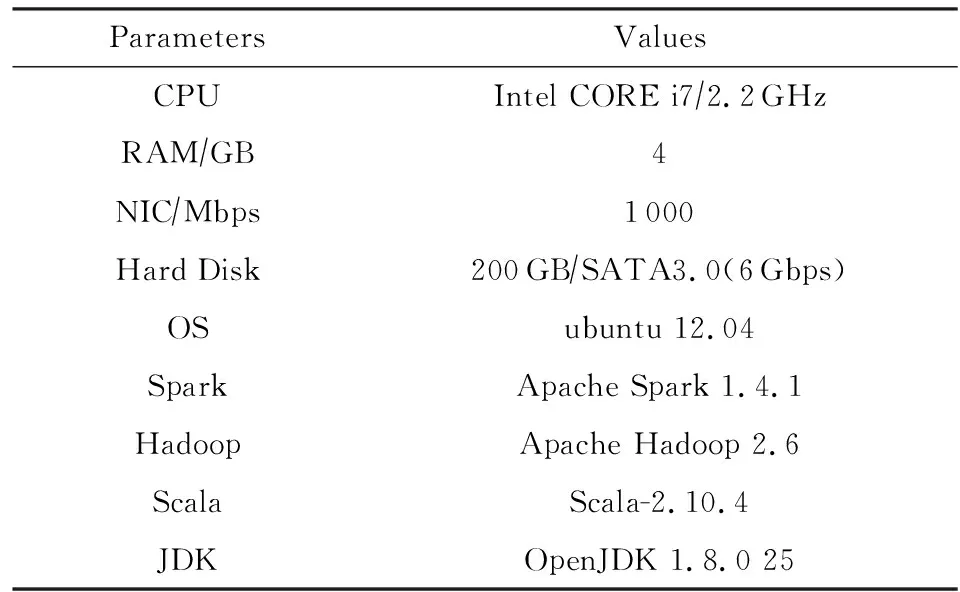
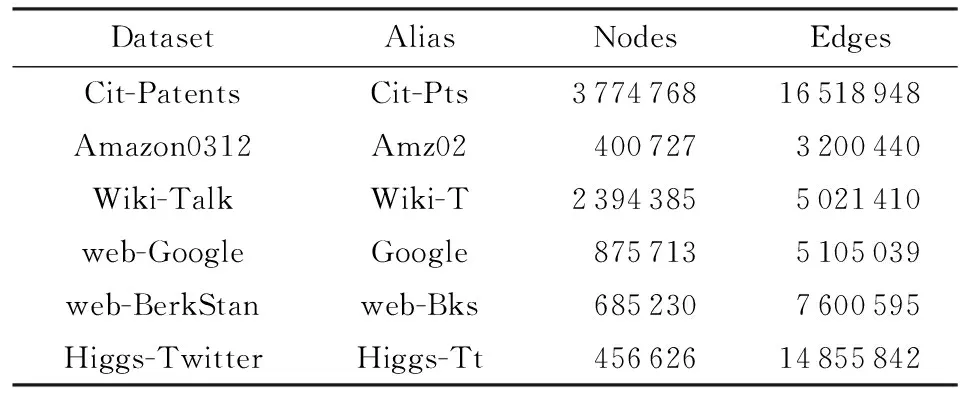
4.1 实验环境
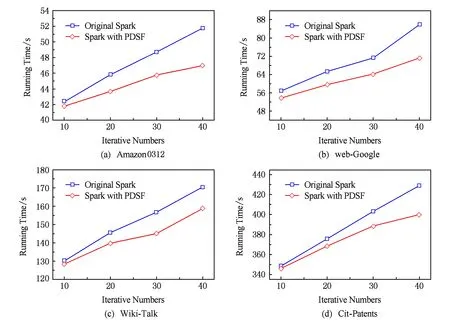
4.2 作业执行效率
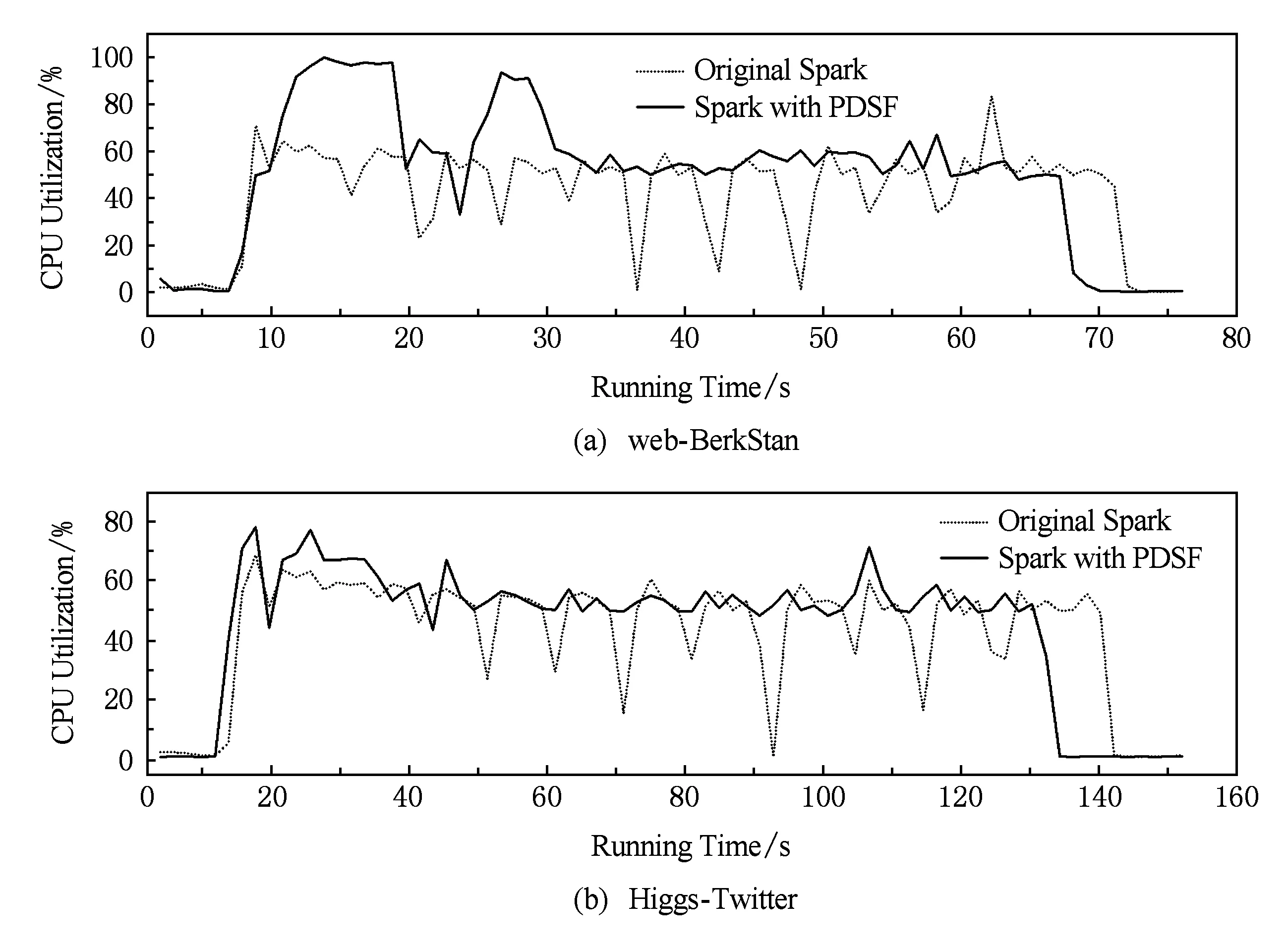
4.3 节点贡献度
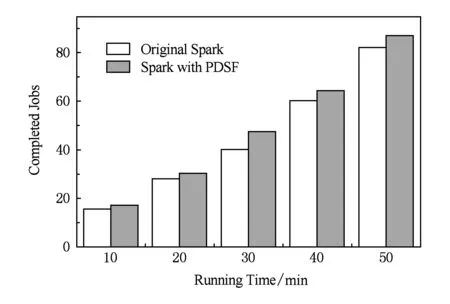
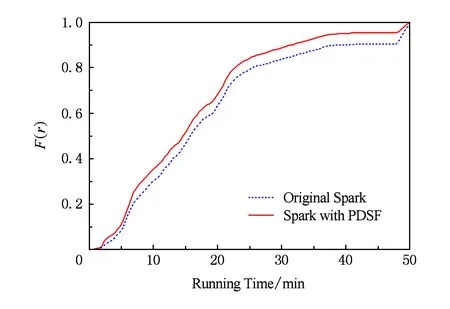
4.4 综合评估
5 总结与展望
