气泡泵压降模型评价研究

蒋丹清，刘道平，陈永军

（上海理工大学制冷技术研究所，上海 200093）

气泡泵压降模型评价研究

蒋丹清*，刘道平，陈永军

（上海理工大学制冷技术研究所，上海 200093）

气泡泵是单压吸收式制冷系统的关键部件之一，其内部工质的流动模拟是气泡泵设计的主要因素，然而在理论计算过程中，存在着两相流模型适用范围有限而模拟精度要求高这一矛盾，因此有必要根据气泡泵特性对现有两相流模型进行适用性评价。本文建立了气泡泵稳态压力降模型，分别对3种均相流压降模型和15种分相流压降模型组合（3种分相流摩阻压降模型分别与5种截面含气率模型组合）进行了模拟计算，并结合饱和水工质下的气泡泵实验数据，将理论值与实验值对比得出误差值进行模型评价。结果表明：Friedel摩阻压降模型结合Zuber截面含气率模型的分相流压降模型的模拟精度最高,适用性最好；均相流压降模型次之，但其计算稳定性最好。

单压吸收式制冷；气泡泵；两相流；模型评价

0 引言

单压吸收式制冷最大的特点之一是使用气泡泵代替常规双压吸收式制冷系统中的溶液泵，其作用是驱动单压吸收制冷系统中的溶液循环，使得系统的内部运行不需要消耗电能。通过提高气泡泵的液体输送能力和能源利用率，可以提升系统的制冷量、系统的性能并扩大系统的适用范围；同时气泡泵具有良好的抗腐蚀性，可以用于输送一些具有腐蚀性和放射性的液体。气泡泵除了被应用于吸收式制冷系统以外，还应用于电子设备冷却技术[1]、微型泵技术[2]、除湿型空调技术[3]、热管技术[4]、太阳能热水系统[5]等领域中。

气泡泵的工作原理如图1所示：加热管底部使部分液体沸腾蒸发，产生的蒸气泡由于浮力的作用上升，并且在上升的同时将提升管内的液体带至更高的水平位置（高位储液器中）；同时由于提升管中存在气体，使得提升管内流体的平均密度比低位储液器中液体的平均密度要小，因此会产生一定压力将提升管内的两相流体。

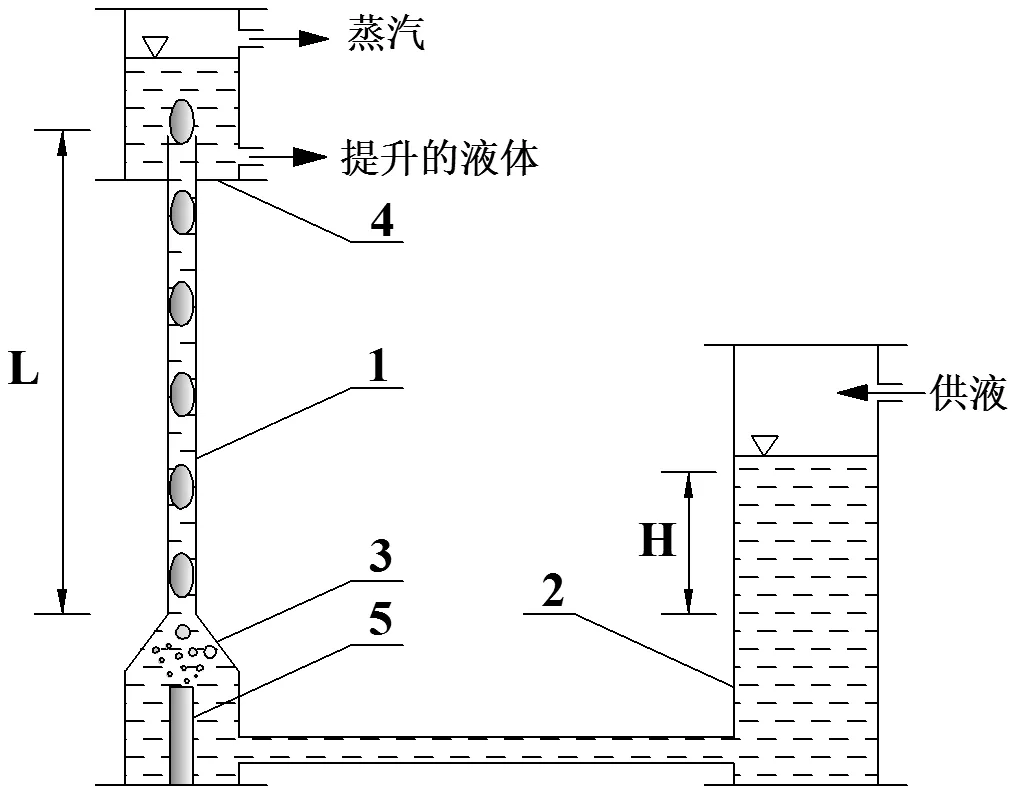
图1 气泡泵的工作原理

气泡泵的流动压头很小，每一部分压降的微小变化都可能引起计算结果相差很大，而现有的两相流模型适用范围有限，大多是经验或半经验公式，因此模型的选取将对气泡泵模拟的结果产生很大影响。

已有很多研究人员对气泡泵进行了理论研究，如 WHITE[6]基于 Einstein制冷循环研究了气泡泵性能，指出提升管内的两相流在由弹状流向块状流过渡时，气泡泵的输送效率最高；CACHARD等[7]用漂移流模型模拟了弹状流下小管径空气提升泵的两相流动；彭一川等[8]忽略局部阻力影响，利用尼克林理论对不同工况下气泡泵性能进行研究提出了空气提升泵的性能计算公式，并通过实验验证了理论模型；薛相美等[9]以氨水为工质，建立了气泡泵的数学模型，并结合实验对气泡泵沉浸比、上升管内径和外部加热功率与气泡泵的提升效率之间的关系进行了研究，其结果对气泡泵最佳设计提供依据。

然而现有的气泡泵理论模型尚无统一的模拟方法对系统进行建模。目前有3种方法进行气泡泵建模：采用能量守恒方程式和动量守恒方程式对空气提升泵系统进行数学建模[10]；基于压力降理论对热虹吸泵进行建模[11-12]；通过实验数据拟合气泡泵液体提升量公式[13-14]。此外两相流模型选取各异，参数选择未加以重视。气泡泵液体提升管是两相并存的流动，其发展至今均基于实验的经验或者半经验公式，每种模型均有一定的限制条件，例如只限定某种流型、某范围压力和流速等。不同模型的计算结果相差甚大，因而有必要重视模型（摩阻压降模型）及参数（截面含气率）的选取。并且针对气泡泵理论模型的适用性及准确性评价未见报道。已有研究人员对现有的两相流模型进行精确性和适用性评价，如FRIEDEL[15]对比了18种截面含气率模型和12种摩阻压降模型，认为Lorchart-Martineili摩阻压降模Hughmark截面含气率模型精度最高，然而针对较低压力，较高流速特征的气泡泵两相流模型准确性未见报道。

因此，本文将针对气泡泵系统中提升管的两相流模型进行研究，选取3种两相流均相压降模型和15种两相流分相压降模型组合（3种分相流摩阻压降模型分别与5种截面含气率模型组合）进行模拟，并与实验数据进行对比，为气泡泵建模过程中两相流模型的选取提供理论性指导。

1 气泡泵压降模型

气泡泵压降包括水平管段单相流压降损失和提升管段两相流压降损失，基于两相流的基本压降理论和系统的压降平衡理论，应用气泡泵流动压头等于整个系统总压降，建立压降模型。

1.1 模型假设

气泡泵两相流复杂，为简化问题，作如下假设：

1) 垂直提升管内的两相流流动为稳定的一维两相绝热流动；

2) 储液器内液位稳定；

3) 忽略气泡泵系统的散热。

1.2 模型建立

气泡泵在稳态条件下，根据其压力特性：流动压头等于整个系统的阻力损失建立数学模型：

其中流动动力为储液器自由液面的位能，即：

式中：

Sflow——流动压头，Pa；

ρl——液体密度，kg/m3。

工质循环过程中，压力降由储液器及连接管中的单相流绝热流动压力降ΔP1和发生器及提升管中的两相流压力降ΔP2组成。

单相绝热流动压力降包括沿程摩擦阻力和局部阻力损失，则：

式中：

λ——沿程损失系数，层流状态下的λ为64/Re；

ρs——单相流体的密度，ρs= ρl；

ke——进口损失系数，ke= 0.5；

kd——出口损失系数，kd= 1；

Ls——中间连接管的长度，m；

Ds——中间连接管的直径，m；

us——连接管内单相流体流速，m/s。

两相流压降由提升管入口处的局部阻力压降和提升管中的压降组成，见式(4)：

气泡泵中的流体是垂直上升流，提升管管径比储液器管径小，因此提升管入口处的压降为突缩接头局部压降，按均相流处理压力损失可表示为：

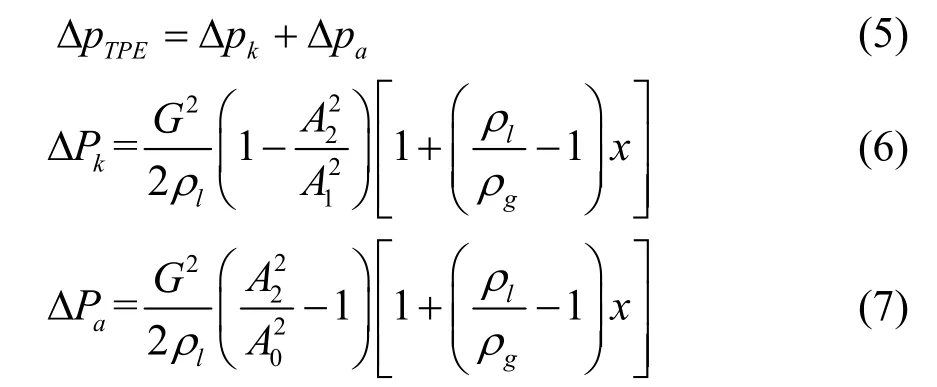
式中：

ΔPk——局部阻力损失；

ΔPa——动能压差；

G——两相流的质量流速，kg/s；

x——质量含气率。

提升管中的压降由摩擦压降ΔPf,重力压降ΔPg,加速压降ΔPm组成，即：

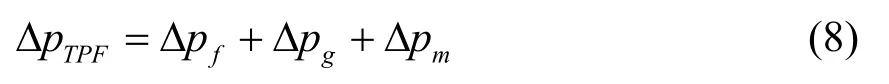
图2为整个管路的各个压力降之间的层次关系。

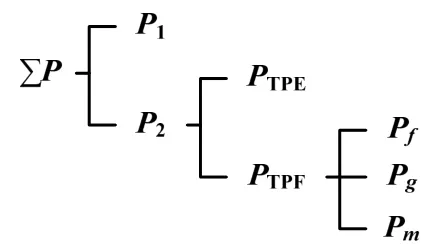
图2 压力损失关系

重位压降ΔPg：

式中：

ρg——气体密度，g/L；

L——提升管管长，m；

α——截面含气率。

加速压降ΔPm影响较小，按分相流加速压降处理可得：

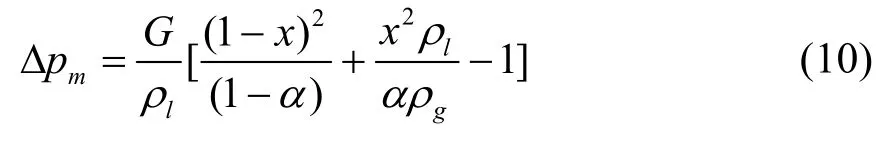
2 两相流模型

2.1 摩阻压降模型

影响摩阻压降的不确定因素很多，因而很难用一般的关系式描述这些影响因素，至今尚无通用公式来描述摩阻压降。本文选用3种典型的均相流模型和3种分相流模型进行评价，分析各模型在气泡泵中的适用性。

2.1.1 均相流摩阻压降模型

均相流模型将两相流体视为平均流体的单向流，两相速度相等，物性参数取两者的平均数。其摩阻压降如式(10)和(11)，平均黏度μ的计算公式如表1所示。

表1 均相流黏度模型

2.1.2 分相流摩阻压降模型

分相流模型假设气液两相处于热平衡状态，速度和压力梯度不相同，有两种计算方法：1）传统法是用“因子”乘以单相摩擦压力梯度，最具代表性的模型是 LOCKHART-MARTINE模型[19]和FRIEDEL模型[15]；2）经验表达式，如MUELLERSTEINHAGEN 模型[20]和 LOMBARDI-CARSANA的CESNDF模型[21]，具体公式如表2所示。

表2 分相流摩阻压降模型

2.2 截面含气率模型

截面含气率 是气液两相流的基本参数之一，在两相流研究中处于重要地位，然而它不可以直接测量，且变化率大，很难用热力学方程来计算，目前的方法大多是经过简化假设,建立模型得出计算关系[23-24]。本文选用5种典型的常用的截面含气率模型经行评价，参见表3。

3 模型评价方法

采用上述建模方法，通过计算软件 EES（Engineer Equation Solver）进行编程求解，物性参数调用软件自带物性参数值，计算出理论液体质量流量。为了验证理论值的精确度，将模拟得出的气泡泵提升液体质量流量结合实验测量的质量流量进行综合评价。分别计算各模型组合条件下的均方根误差S和标准偏差M，如式(12)和式(13)。

4 模型评价结果及分析

选取测量精细、可靠性较高的平亚琴等[30]对导流式气泡泵进行实验研究）实验数据。其具体的实验工况如下：系统压力为1个大气压，加热功率为200 W～400 W，沉浸比控制在0.2～0.5，以饱和水为工质，共计25个工况点。应用不同模型分别计算各个工况下的质量流量，并将理论值与实验值进行比较。图3所示为采用FRIEDEL分相流摩阻压降模型[15]结合 ZUBER截面含气率模型[29]模拟图，横坐标为液体提升量实验值，纵坐标为理论预估值，误差在±20%，理论值和实验符合较好。表4和表5为每种模型下的均方根误差和标准偏差计算结果。由表4可知，均相流模型中3种平均黏度模型的模拟结果相差不大，且标准偏差较小，计算稳定性较好。

表3 截面含气率模型

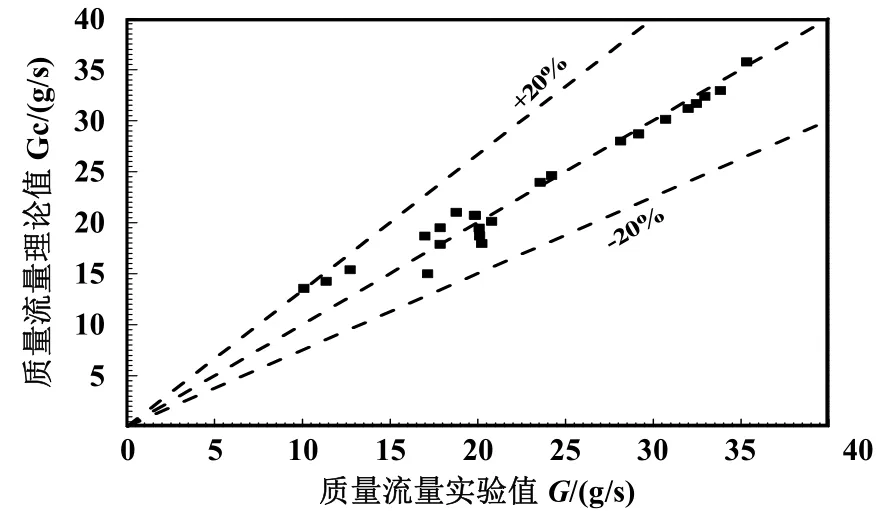
图3 质量流量理论值和实验值（Friedel摩阻模型结合Zuber截面含气率模型模拟）

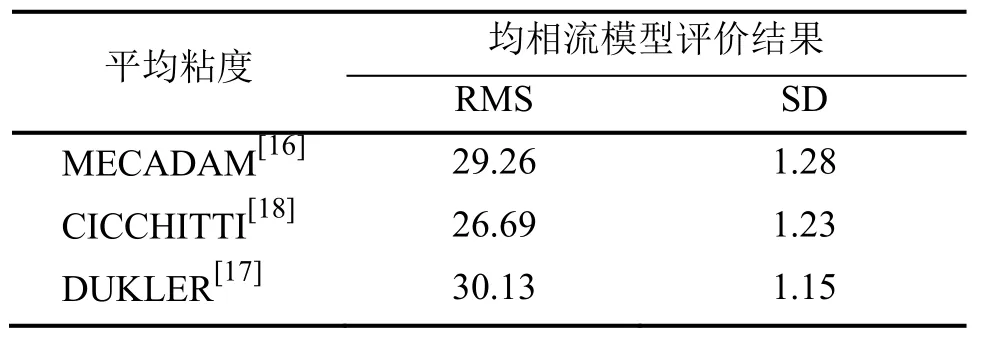
表4 均相流摩阻压降模型评价

表5 分相流摩阻压降模型结合截面含气率模型评价

4.1 摩阻压降模型评价结果与分析

图4为相同截面含气率下不同摩阻压降模型的评价结果。从图中可知，FRIDEL分相流模型[15]的模拟精度最高，M-S摩阻压降模型和均相流摩阻压降模型[20]次之，CHISHOLM模型[22]模拟精度最差。原因可能是FRIEDEL压降模型[15]在湍流区适用性较好，气泡泵工作时两相流处于湍流，因此匹配度高，而CHISHOLM模型[22]在低压、低质量流速适用性较好，气泡泵压力和流速较高，因此模拟精度最差。因此在气泡泵建模过程中，推荐采用FRIDEL分相流模型[15]计算摩阻压降。比较各摩阻压降模型的标准偏差值，对比发现均相流模型的标准偏差最小，说明其离散度小，计算稳定性最好。

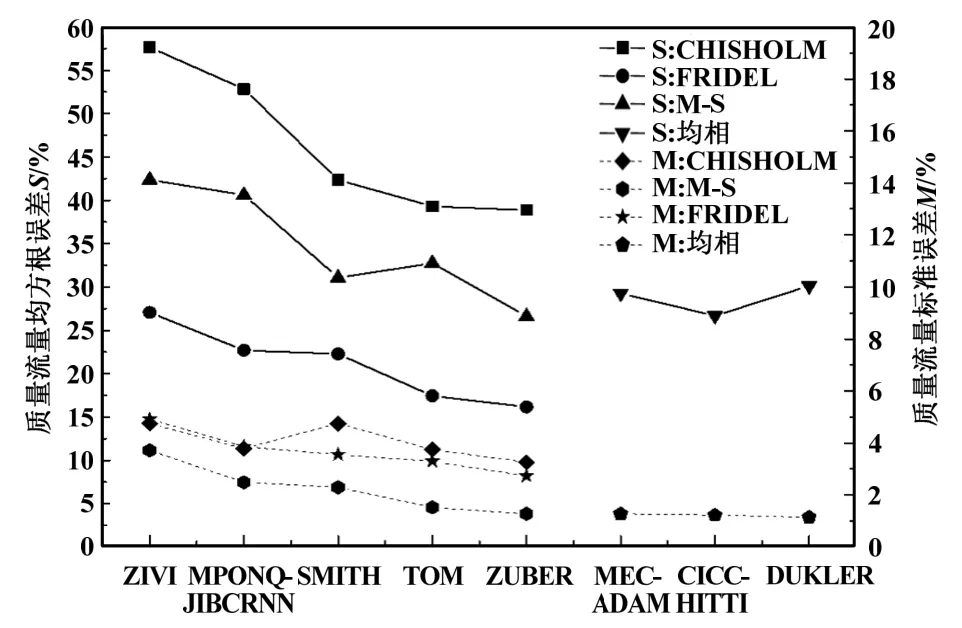
图4 摩阻压降模型的评价结果

4.2 截面含气率模型评价结果与分析

图5为相同压降模型下不同截面含气率模型的评价结果，从图中可以看出所有分相流模型中ZUBER漂移流截面含气率模型[29]模拟精度最高，ZIVI最小熵增模型[28]模拟精度最差。CHISHOLM分相流模型[22]和FRIDEL分相流模型[15]中TOM变密度截面含气率模型次之，而 M-S分相流模型[20]中SMITH混相-单相截面含气率模型[26]次之。因此在气泡泵建模过程中，建议使用ZUBER漂移流截面含气率模型[29]进行模拟。

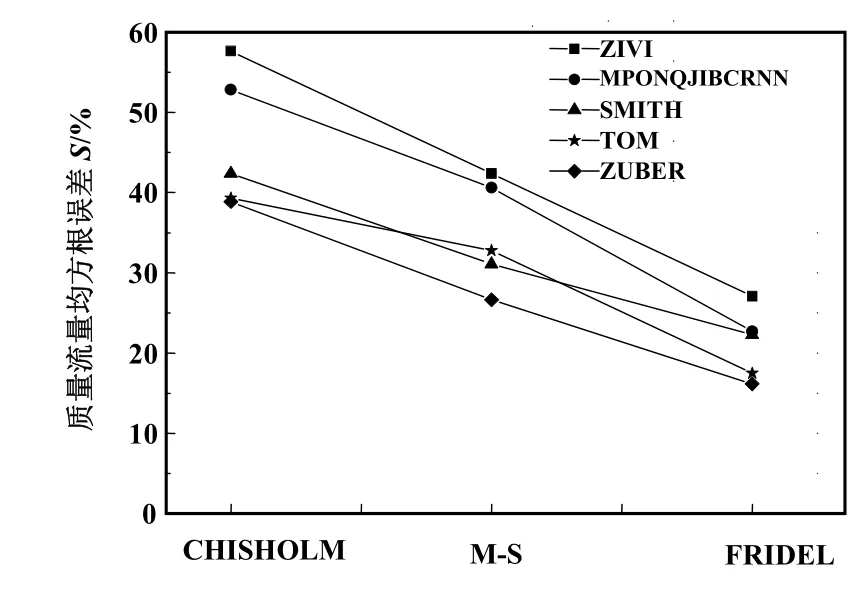
图5 截面含气率模型的评价结果

5 结论

为解决气泡泵两相流计算复杂，模型适用范围小导致的模拟结果差异大这一问题，通过实验对 3种均相流摩阻压降模型和 15种分相流模型进行了评价，结果表明：

1) FRIEDEL分相流摩阻压降模型模拟精度最高，适用性最好，可能原因为模型在湍流区适用性较好，气泡泵工作时两相流处于湍流，因此匹配度最高；

2) ZUBER截面含气率模拟精度最好，究其原因可能是因为此模型考虑因素较多，分别考虑了表面张力、粘度和管道尺寸等因素，因而适用性较好；

3) 综合考虑截面含气率和摩阻压降模型FRIEDEL摩阻压降模型结合ZUBER截面含气率模型的模拟精度最高,适用性最好；均相流摩阻压降模型次之，但其计算稳定性最好。

[1]KUO S C, SHIH C C, CHANG C C, et al. Bubble pump in a closed-loop system for electronic cooling[J]. Applied Thermal Engineering, 2013, 51(5): 425-434.

[2]TORNIAINEN E D, GOVYADINOV A N, MARKEL D P, et al. Bubble-driven inertial micropump[J]. Physics of Fluids, 2012, 57(4) : 24-29.

[3]赵巍, 阚怡松, 朱瑞琪. 除湿型空调中气泡泵的试验研究[J]. 流体机械, 2002, 30(4): 55-58．

[4] 韩晓红, 闵旭伟, 李鹏, 等. 一种利用气泡泵效应重力辅助回路热管的实验研究[J]. 西安交通大学学报,2012, 46(3): 9-14.

[5]ZHANG Q, STEWART S W, BROWNSON J R S.Bubble pump modeling for solar hot water heater system design optimization[J]. The Penn State McNair Journal,2011, 18(3): 167-187．

[6]WHITE S. Bubble pump design and performance[D].Atlanta: Georgia Institute of Technology, 2001.

[7]CACHARD F, DELHAYE J M. A slug-churn model for small-diameter airlift pumps[J]. Internal Multiphase Flow,1996, 22(4): 627-649.

[8]彭一川, 肖泽强. 气泡泵起现象的理论和实验研究[J].东北工学院学报, 1989, 10(2): 111-117．

[9]薛相美, 刘道平, 王汝金. 单压吸收式制冷技术的研究进展[J]. 制冷与空调, 2008, 8(5): 30-34.

[10]CLARK N N, DABOLT R J. A general design equation for air-lift pumps operating in slug flow[J]. AICHE Journal, 1986, 32(4): 56-64.

[11]李跃智, 吴裕远, 王鹏飞, 等. 无泵溴化锂吸收式制冷机小型化研究[J]. 制冷技术, 2003, 23(4): 16-18.

[12]戴永庆, 耿惠彬, 蔡小荣. 溴化锂吸收式制冷技术的回顾与展望[J]. 制冷技术, 2001, 21(1): 21-24.

[13]DELANO A. Design analysis of the Einstein refrigeration cycle[D]. Atlanta: Georgia Institute of Technology, 1998.

[14]钱子敏. 双效溴化锂吸收式制冷机的优化设计[J]. 制冷技术, 1988, 8(3): 16-19.

[15]FRIEDEL L. Improved friction pressure drop correlations for horizontal and vertical two-phase pipe flow[C].European two-phase flow group meeting, 1979.

[16]MCADAMS W H. Trans[J]. ASME Journal, 1942, 64(3):193-197.

[17]DUKLER A E. Self-diffusion, mass transfer, and viscosity coefficients for a binary mixture in narrow slit-like pores[J]. AICHE Journal, 1964, 10(1): 38-51.

[18]CICCHITTI A. Modeling of fluid taking account of viscosity[J]. Engineer Nuclear, 1960, 7(6): 407-425.

[19]LOCKHART R W, MARTINELLI R C, CHEMMA W H,et al. Momentum flux on two-phase flow [J]. ASME Journal, 1968, 2(1): 147-158

[20]MUELLER W L, STEINHAGEN G B. Two-phase pressure gradient[J]. International Development in Heat Transfer, 1963, 25(1): 363-368.

[21]LOCKHART R, MARTINELLI R. Proposed correlation of data for isothermal two-phase, two-component flow in pipes[J]. Chemical Engineering Progress, 1949, 45(1):39-48.

[22]CHISHOLM D. The influence of mass velocity on friction pressure gradients during steam-water flow[J].Institute of Mechanical Engineers, 1968, 3(5): 401-413.

[23]MÜLLER-STEINHAGEN H, HECK K. A simple friction pressure drop correlation for two-phase flow in pipes[J]. Chemicaluu Engineering and Processing:Process Intensification, 1986, 20(6): 297-308.

[24]LOMBARDI C, CARSANA C. Dimensionless pressure drop correlation for two-phase mixtures flowing up-flow in vertical ducts covering wide parameter ranges[J]. Heat and Technology, 1992, 10(1): 125-141．

[25]MPONQJIBCRNN E H. Heat and Mass Transfer [J].Technology Presentation, 1971, 37(5): 61-64.

[26]林宗虎. 气液两相流和沸腾传热[M]. 西安: 西安交通大学出版社, 2003．

[27]TOM S G. Heat and Mass Transfer [J]. ASME Journal of Fluids Engineering , 1964, 82(4): 265-270.

[28]ZIVI S M. Heat and Mass Transfer [J]. ASME Journal of Fluids Engineering, 1966, 86(2): 247-251.

[29]ZUBER N, FINDLAY J A. Heat and Mass Transfer [J].ASME Journal of Fluids Engineering, 1965, 87(4):453-457.

[30]平亚琴, 刘道平, 陈盛祥, 等. Einstein循环制冷机导流式气泡泵的性能研究[J]. 热能动力工程, 2011, 26(6):743-746.

Investigation on Evaluation of Pressure Drop Models for Bubble Pump

JIANG Danqing*, LIU Daoping, CHEN Yongjun
(Institute of Refrigeration Technology, University of Shanghai for Science and Technology, Shanghai 200093, China)

The bubble pump is one of the key components of single pressure absorption refrigeration system, and the internal flow simulation of refrigerant is its main design factor. In theoretical calculation, the existing two phase models are not accurate enough for the simulation of the bubble pump. Therefore, it is important to make an assessment of existing pressure drop models corresponding to the bubble pump. Lots of available mathematical models of the bubble pump were evaluated in this paper, including three homogenous pressure drop models and fifteen separated phase pressure drop combination models (3 separated phase frictional pressure drop models separately combining with 5 representative void fraction models). Comparing simulation results with experimental results based on the working fluid of saturated water, it was found that the separated phase pressure drop model with Friedel frictional pressure drop model and Zuber void fraction model is the best one. Meanwhile,the homogenous pressure drop model can work better than all others due to good reliability.

Single pressure absorption refrigeration; Bubble pump; Two phase flow; Model evaluation1

10.3969/j.issn.2095-4468.2017.04.104

*蒋丹清（1990-），女，硕士研究生。研究方向：低温与制冷空调。联系地址：上海市杨浦区军工路516号上海理工大学，邮编：200093。联系电话：18420138069。E-mail：18301921379@163.com。

上海市研究生创新基金项目（No.JWCXSL1302），上海市教育委员会科研创新项目资助（No.13ZZ117）。1