谐振法测量圆管状样品复介电常数典型结构的解析模型

2017-11-07罗辉华

中国测试 2017年10期

关键词：谐振腔介电常数谐振

匡轮，罗辉华，匡尧

（1.北京无线电测量研究所，北京100039；2.北京大学数学科学学院，北京 100871)

谐振法测量圆管状样品复介电常数典型结构的解析模型

匡轮1，罗辉华1，匡尧2

（1.北京无线电测量研究所，北京100039；2.北京大学数学科学学院，北京 100871)

针对圆环形介质元件制作在线监测的需要，提出用谐振法直接测试圆管状绝缘介质复介电常数的思路。提出4种可能的谐振结构形式，其中推演介质加载圆柱腔TM010模式谐振的解析模型，深入分析国外文献关于介质加载圆柱腔TE011模式谐振问题的理论结果，并对介质加载圆形同轴腔的特性方程用于复介电常数测量的问题进行探讨。对各个解析模型进行计算，并相应地与文献的实验结果进行对照,吻合良好。结果表明：TM010模式的解析模型正确；谐振特性参数对加载介质复介电常数（εr=1～80，tanδ=10-5～10-4)的敏感性随结构的不同而不同。最终得出：圆柱腔TM010模式可用在谐振法测试圆管状绝缘介质元件的复介电常数中。

复介电常数；谐振测试法；圆管样品；解析模型；基模

0 引言

谐振法是测量介质介电常数的常用方法，如小棒测试法[1-3]、薄片测试法[4]、块状样品测试法[5-6]等。它们分别对不同形状的实心样品的复介电常数的测量问题建立了电磁模式的解析模型（TM、TE或TEM等，大多为基模)。对于圆管状介质样品（空心样品)，虽然可以用圆柱谐振腔、圆形同轴谐振腔加载的结构实施复介电常数的测试，但相应的理论研究和实验报道很少。文献[7]报道了TE011模式下的理论分析公式和实验数据，但未给出对应实验数据的理论计算结果，也未进行TM模式的分析或实验。我国学术界关注到了该论文[8-9]，但没有相应的研究或应用报道。文献[10]采用低介电常数小管状介质作为容器，测量存于其中的动物组织的介电常数，但不是对小管本身的介电常数测量，也没有进行电磁模式的解析分析。早期有学者对同轴谐振腔加载圆环介质的问题进行了分析[11]，但未考虑介质介电常数的测试问题。其他测试法如传输线特性测试法[12]、自由空间照射法[13]等，也难以借用到对圆管状元件的测量。

在介质谐振器、微波铁氧体带线结环行器内部结构及有源集成天线（active integrated antennas，AIAs)中，天线谐振元件的制作过程中大多需要对介质的微波介电常数进行测量，最好是对圆管状元件进行在线测量。考虑到技术应用所需，本文拟对尚未见诸报道的空心样品的谐振法测试建立TM模式解析模型，并进行理论计算与实验结果对照；针对TE模式谐振特性，深度分析文献[7]的解析结果；对TEM模式则主要进行模型特性计算。通过分析、计算和对比，获得谐振法测量圆管状介质样品复介电常数的典型结构和模式一般特性的知识。

1 原理

在谐振法测量介质介电常数的测试线路中，其核心部件是加载了该介质的谐振腔。相对于空腔（未加载该介质)，加载了该介质样品的腔的谐振频率、品质因数都将发生变化。通过电磁场理论分析得到谐振特性方程后，即可通过实验数据计算得到介质的复介电常数。谐振特性方程既包含了结构参数、介质复介电常数，也包含了电磁场模式。从轴对称圆形腔结构来看，要得到解析结果，必须轴向、环向和径向三者中最多只有一向是非均匀的；而使用基模会有诸多便利。因此本文仅限于讨论基模工作、只有径向不均匀或者轴向不均匀的情形。

测试圆管状介质样品复介电常数的圆谐振腔通用结构如图1所示。圆柱腔内表面层的磁导率、电导率分别为μc、σc。圆形封闭谐振腔内区域分为3部分：

图1 圆形谐振腔法测试的通用结构简图（旋转对称)

III区：b≤r≤a，μ3、ε3（通常为空气)；

II区：c≤r≤b，μ2、ε2（分别为待测元件的磁导率、介电常数)；

I区：r≤c，有 2 种情况：r≤c整体为一种低介电常数绝缘介质，以 μ1、ε1表征；r≤d 内为金属柱，d～c为薄层低介电常数绝缘介质，仍以μ1、ε1表征。

2 方法

这里对4种典型结构进行分析，以获得其谐振频率满足的方程和品质因数满足的方程。

2.1 结构1：小长径比圆柱腔，谐振基模TM010

本结构中高度h＜2a，I区为r≤c整体。对本结构从一般的电磁场理论入手，结合边界条件进行分析和建立数学模型，只考虑基模。

设场量如下（只有Ez，Hφ非0；轴向z方向均匀，传播常数β=0)：

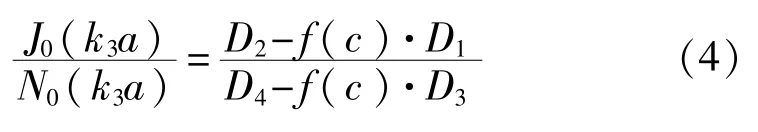
设E1已知，可求得：

腔侧壁趋肤效应电阻损耗功率为

腔上下底壁趋肤效应电阻损耗功率为

其中ωs，ω0分别为加载样品时和空腔时的谐振角频率，分别为ω0下腔内壁的表面电阻和趋肤深度；积分项

加载后腔体部分的品质因数Qsc=ωs·We/（Pc1+Pc2)；被测样品谐振腔的品质因数为Qs，有：

2.2 结构2：大长径比圆柱腔，谐振基模TE011

本结构中高度h往往大于2a，I区为r≤c整体。对本结构直接借用文献[7]的相关结论，但应用于本情形时，考虑到k1为虚数，需进行虚宗量、实宗量Bessel函数之间的转换，只考虑基模。

Geyer等采用I区为很高的介电常数（待测)绝缘介质、II区为介电常数已知的圆管状样品，得到TE01u模式谐振频率的特征方程（文献[7]式（12))。当I区为低介电常数绝缘介质时推演该方程，得到：

2.3 结构3：圆形同轴腔，谐振基模TEM，介质在径向部分填充但轴向满填充

本结构I区为金属圆柱（r≤d)并外套薄层绝缘介质（d～c)。当a不太大且不出现TM、TE模式时，可以考虑先用等效电容法（内导体到外导体之间电容串联)来获得等效介电常数[14]，然后用同轴传输线的相关特性参数来获得介质复介电常数的表达式。

令 εe=εe′-jεe″。对半波长谐振器（λs=2h)有：

其中 si=gi（g1/ε1′+g2/ε2′+g3/ε3′)/εi′， g1=ln（c/d)，g2=ln（b/c)，g3=ln（a/b)。

2.4 结构4：圆形同轴腔，谐振基模TEM，介质在径向满填充但轴向部分填充

本结构I区为金属圆柱（r≤d)，无薄层介质，被测样品在轴向上只占取一段（设从端头开始)，但充满该段内外导体之间的区域。

假设两段的长度、所在区域绝缘介质的磁导率、介电常数和传播常数分别为 li，μi，εi，βi，i=1，2，其中。设l2段为被测绝缘介质，有谐振条件及介电损耗角正切表达式[11]为

3 结果与讨论

3.1 解析模型分析

1)对结构1得出的解析模型，容易推演出c→0时 f（c)→0，式（4)化为普通的特征方程表达式（实心样品)；同时，取I区的介质参数与II区的介质参数相同时也得出同样的结果。因此，本结构下得出的数学模型是准确的，但显然空心使得特征方程更加复杂。

由于空心的情况没有相应的实验或理论报道数据，本文取其特殊情形c=0 mm（实心)，针对文献[3]样品1#的实验参数进行计算：取b=0.8 mm，h=10.16 mm，a=12.04 mm，Q0（ω0)=7 482；ω0=2π·9.531 2 GHz；tanδ2=7.36×10-4，ωs=2π·8.334 6 GHz，得到 ε2/ε0=15.4，Qs（ωs)=6757。 ε2/ε0计算结果与该实验结果（15.8)相差2.5%，其他数据吻合；与同一根圆棒上切下的样品用Courtney法测量的实验结果（15.53)相差小于1%。

2)对结构 2，式（10)与文献[7]对应的式（51)有所不同。为了辨别二者的对错，本文取文献[7]的实验数据进行对比计算：c=5 mm，b=30 mm，h=45 mm，a=50 mm，TE011模式。按式（10)，取腔内壁电导率σc=5.8×107/Ωm；I区和 III区均为干燥空气，II区介质 ε2/ε0=37.2，tanδ2=1.9×10-5，求出 ωs=2π·0.94 GHz，Qs（ωs)=13 151，与文献[7]的实验数据吻合良好（2π·942MHz，13200)。但按文献[7]的式（51)得不出谐振频率（实验参数式（51)不成立)，且其作者也没有给出该实验的理论计算结果。分析发现，该作者在虚、实宗量Bessel函数的变换上出现了差错，导致了该特性方程错误，而式（10)是正确的。

3)同轴谐振腔的解析模型求解谐振频率显得简单得多，介电损耗的求解也相对简单。

4)从测量加载介质的复介电常数的角度看，希望测量结构的谐振参数对复介电常数尽量敏感，但是本文4种结构的解析模型均看不出敏感的程度，需要进行数值计算。

3.2 典型样品尺寸下各解析模型计算结果分析

取典型尺寸圆管状样品作为计算例，分别用上述4种解析式计算谐振频率和品质因数，对比见图2～图4。除特别说明外，取腔内壁电导率σc=4.9×107/Ωm；III区为干燥空气，II区介质tanδ2=0.0005。

结构 1：取 c=7.5 mm，b=10 mm，h=84 mm，a=96mm，ω0=2π·1.1953GHz，Q0（ω0)=21542；取 c=2mm，b=5 mm，h=45 mm，a=50 mm，ω0=2π·2.294 9 GHz，Q0（ω0)=15780。

结构 2：取 c=5mm，b=30mm，h=45mm，a=50mm，tanδ2=0.0005。

结构 3：取 d=7mm，c=7.5mm，b=10mm，l2=28mm，h=84mm，ωs=2π·1.78446GHz。 ε1/ε0=2.25，tanδ1=0.0001。a=13.6 mm（大约为使TEM模式工作频率最高的尺寸)；a=35mm（大约为使 Qs最高的尺寸)。

结构 4：取 d=c=7.5 mm，b=10 mm，h=68 mm，l2=28mm。

图2 谐振频率随介电常数变化的曲线（ωs=2πfs)

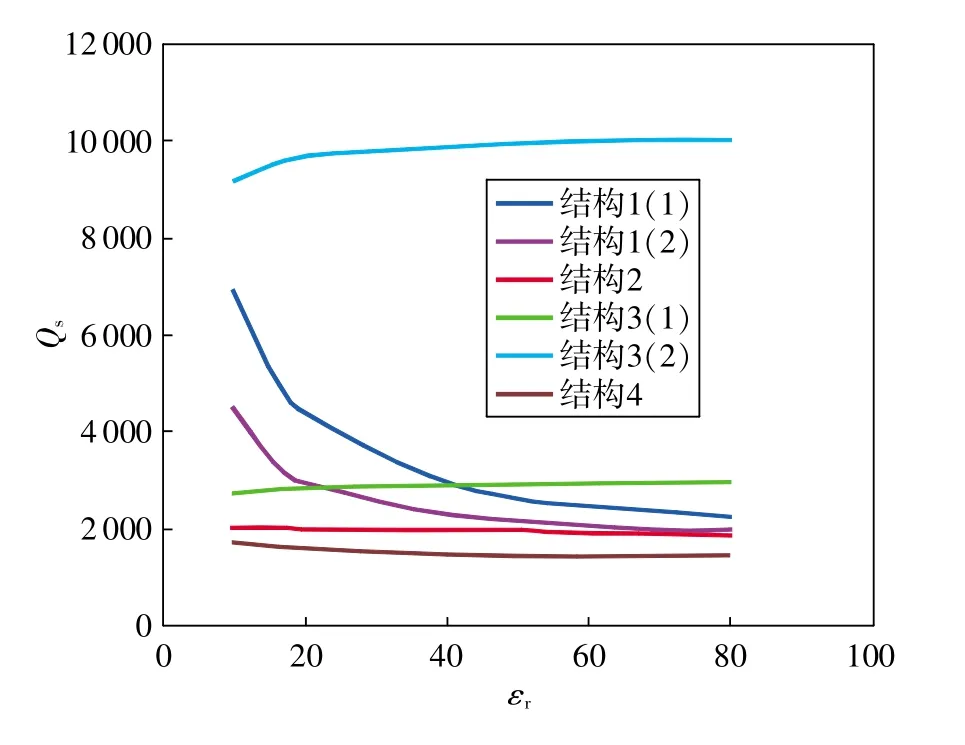
图3 谐振品质因数随介电常数变化的曲线

图4 谐振品质因数随介电损耗变化的曲线

在εr=1～80范围内分析发现：

1)εr越高，谐振角频率ωs对其变化的敏感性越低。在εr=1～10范围内，结构2的敏感性最高，但在εr=1～80范围内整体看，结构1的敏感性更好一些；结构3敏感性最低。

2)εr越高，品质因数Qs对其变化的敏感性越低。结构1的敏感性最高，结构2敏感性最低，结构3在a较大时Qs最高，但在a较小时Qs低；结构4的Qs最低。

3)谐振系统品质因数Qs对介质的tanδ的敏感性，结构1为最高，结构3和结构4分别在εr=1～50和εr=50～80 内最低。

4)在算例区间内，样品尺寸没有使4种结构的解析模型彼此的相对特性发生变化。换言之，优势的结构对不同尺寸的样品都呈现优势。

上述各计算例谐振频率均不高，如果采用高阶模式谐振，将有可能在10GHz以上获得相应的测试数据[15]。适当加载介质环后测量其复介电常数是可实现的。

4 结束语

本文推演得出了结构1（圆柱谐振腔TM010模式)下谐振法测量圆管状介质样品复介电常数的数学模型，纠正了文献[7]对结构2（圆柱谐振腔TE011模式)谐振法测量其数学模型中的错误，并对圆形同轴腔的谐振特性方程（用于测量复介电常数)进行了分析和计算。结果表明，当εr在1～80范围内时，结构1及其数学模型用于谐振法测试是可行的；εr在1～10范围内时，结构2及其数学模型用于谐振法测试是可行的。结构3、结构4（同轴谐振腔，基模)及其数学模型均不适合于测量介电常数和介电损耗。

[1]SHEEN J.Amendment of cavity perturbation technique for loss tangent measurement at microwave frequencies[J].Journal of Applied Physics，2007，102（1)：249-1642.

[2]IKEDA M，NISHIDA K，SHIMASAKI H，et al.Influence of the coupling between a cavity and a transmission line on the measurement of complex permittivity by the resonant cavity perturbation method[C]∥Asia-pacific Microwave Conference，2008.

[3]匡轮，徐翔，张婷，等.GB9633标准测量微波铁氧体介电常数方法的再探讨[C]∥第十六届全国微波磁学会议论文集，2013.

[4]NOSKOV Y N.Method for measuring properties of high relative dielectric constant materials in a cutoff waveguide cavity[J].IEEE Trans.Microwave Theory and Technique，2000，48（3)：329-333.

[5]许栩.低损耗材料分离介质谐振器法复介电常数测试[D].成都：电子科技大学，2009.

[6]KIM S，JARVIS J B.An approximate approach to determining the permittivity and permeability near halfwavelength resonances in transmission/reflection measurements[J].Progress in Electromagnatics Research B，2014，58（58)：95-109.

[7]GEYER R G， KABOS P， JARVIS J B.Dielectric sleeve resonator techniques for microwave complex permittivity evaluation[J].IEEE Trans Instrument Measurement，2002，51（2)：383-392.

[8]何小瓦，李恩，张其劭，等.介质材料复介电常数变温测量技术综述[J].宇航材料工艺，2005，35（1)：20-23.

[9]倪尔瑚.介质谐振器的微波测量[M].北京：科学出版社，2006：137-144.

[10]SAITO H， SUZUKI Y， TAK M.Measurement of complex permittivity for biological cells by waveguide penetration method[C]∥European Conference on Antennas&Propagation，2009.

[11]HORNER F， TAYLOR T A， DUNSMUIR R， et al.Resonance method of dielectric measurement at centimeter wavelength[J].Joural of the Institution of Electrical Engineers-Part III：Radio and Communication Engineering，1946，93（21)：53-68.

[12]KIM S，GUERIERI J R.Low-loss complex permittivity and permeability determination in transmission/reflection measurements with time-domain smoothing[J].Progress in Electromagnatics Research M，2015（44)：69-79.

[13]SKOCIK P，NEUMANN P.Measurement ofcomplex permittivity in free space[J].Procedia Engineering，2015（100)：100-104.

[14]张晓勇，谢普，虞春，等.50Ω编织外导体射频同轴电缆的设计[C]∥光缆电缆学术年会论文集，2003.

[15]董玉和.微波圆柱和同轴腔高阶横磁模式及其输出耦合[D].北京：中国科学院电子研究所，2006.

Analytical model of typical structures in resonance measurement on the complex permittivity of tubular sample

KUANG Lun1， LUO Huihua1， KUANG Yao2
（1.Beijing Institute of Radio Measurement，Beijing 100039，China；2.School of Mathematical Sciences，Peking University，Beijing 100871，China)

For the on-line monitoring demands of circular dielectric element manufacturing，the idea is put forward that the resonance method can be directly applied to test the complex permittivity of tubular insulating medium.Four kinds of resonance structures forms are proposed，and the analytical model of resonance in dielectric loaded cylindrical cavity TM010mode is derived;the theoretical results for a TE011mode resonant cavity in foreign literature are analysed deeply and the application of the characteristic equations of dielectric loaded circular coaxial cavities to the measurement of the complex permittivity is also explored.Besides，calculations are done for analytical models and they are accordingly compared with literature test results，which are identical.As a result， the analytical model of TM010mode is right， and the sensitivity of the resonant characteristics to the complex permittivity of loaded dielectric（εr=1-80， tanδ=10-5-10-4)，differs from one structure to another.Finally，the results show that cylindrical cavity TM010mode can be used in the measurement of complex permittivity of resonant measurement for the complex permittivity of tubular insulation dielectric element in resonance method.

complex permittivity； resonant measurement； tubular sample； analytical model； basic mode

1674-5124（2017）10-0001-05

10.11857/j.issn.1674-5124.2017.10.001