LOS MIMO系统多相位跟踪与补偿

罗丽平，周景荣， 陈海强

(1.广西民族大学信息科学与工程学院，广西 南宁 530006；2.中山大学电子与信息工程学院，广东 广州 510275；3.广西大学计算机与电子信息学院，广西 南宁 530004)

LOS MIMO系统多相位跟踪与补偿

罗丽平1，周景荣2， 陈海强3

(1.广西民族大学信息科学与工程学院，广西 南宁 530006；2.中山大学电子与信息工程学院，广东 广州 510275；3.广西大学计算机与电子信息学院，广西 南宁 530004)

针对LOS MIMO系统中分布式天线的多个发送端相位噪声和多个接收端相位噪声，基于LMS准则和线性均衡提出了多相位跟踪与补偿算法，通过仿真分析了该算法在不同的振荡器配置、相位噪声带宽、调制阶数和迭代步长下系统的误符号率性能。并与基于锁相环的多相位跟踪算法(PLL)作比较，结果表明：LMS算法的误符号率性能明显优于PLL算法，能有效降低LOS MIMO系统的误符号率，且更具有实用性。

LOS MIMO系统；LMS准则；线性均衡；多相位噪声；跟踪与补偿

随着移动网络由3G向4G甚至5G的不断演进，网络最后一公里接入的速度不断提高，网络变得越来越密集[1]。而承载着将基站内所有通信链路与核心网络连接功能的回程网络(Backhaul network)，作为一种灵活和低成本的方式，被认为是一种较好的解决方法，已经得到了越来越多的认可和重视。但，这项技术也将面临越来越大的挑战[2]。在现有的无线回程网络技术中，微波系统(如6～38 GHz)因具有很宽的传输带宽，是较为常用的一种无线回程技术[3]。载频更高和频带更宽的毫米波技术(如60 GHz)也是一种可能的无线回程技术[4]。但由于频谱的稀缺性和高成本，实际中却难以通过不断增加传输带宽来提高回程效率。与通过增加频谱方式不同，多输入多输出(MIMO：multiple-input multiple output)技术[5]利用空间维度来提高传输效率，并已经在接入网络(LTE：long term evolution)和WLAN(wireless local area network)中得到了广泛使用[6]。近年来，将微波或毫米波与MIMO技术相结合，以进一步提高无线回程网络的传输效率成为了研究的热点[7-10]。在传统的MIMO系统中，非视距(NLOS：non-light of sight)传输和丰富的散射环境是MIMO技术得以成功的关键因素[5]。与此不同，在微波和毫米波系统中，视距(LOS：light of sight)传输是主要的传输径，这对微波或毫米波系统与MIMO技术的结合带来了挑战[7]。文献[7]证明：通过优化天线的布置，即使在LOS传输环境中也可实现MIMO复用传输。

实现MIMO复用传输在微波或毫米波系统中的应用，要求天线之间保持足够的间隔，其距离一般达到数米[7]。因此，不同的天线必须采用不同的振荡器。然而，天线系统中的振荡器会带来相位误差(PHN：phase noise)[11]。在传统的MIMO系统中，由于发送端或接收端均使用共用的振荡器，发送端和接收端均只有一个相位，所以只需进行单个相位的估计和补偿[12]。在微波或毫米波系统中，不同天线之间的相位噪声是相互独立的，因此微波或毫米波MIMO系统面临更高的挑战[3,10,13]。文献[3,10]分析了相位噪声对基于LOS传输的MIMO系统容量的影响。文献[13]通过实验验证了多个独立的相位噪声对基于MIMO的微波或毫米波系统误码率性能的影响，其结果证明了进行多相位跟踪和补偿的必要性和重要性。此外，文献[13]针对接收端多根天线共用振荡器的情形，提出了利用多个平行的锁相环算法来进行多相位的跟踪。实际中的分布式天线系统更多是采用不同的振荡器来产生无线信号。因此，如何同时实现LOS MIMO系统中分布式天线多个发送端相位和多个接收端相位的跟踪与补偿，是一个非常重要和现实的问题。

1 系统模型

1.1 双极化LOS MIMO信道模型

考虑Nr×NtLOS MIMO信道矩阵[14]，

(1)

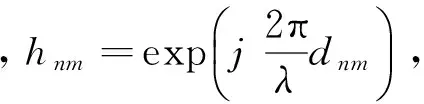
文献[14]提出采用极化天线能提高复用增益。对2×2天线系统，采用双极化天线可以实现4×4天线系统，其信道矩阵可表示为克罗内克积(Kronecker product)形式：

理想情况下，极化天线之间是相互正交的。然而，实际中由于周围环境的变化，如天气等，难免会出现能量泄露，从而导致一定的性能损失。其中α为能量泄漏因子，与之相对应的交叉极化差别(XPD: cross-polarization discrimination)定义为XPD。

1.2 LOS MIMO系统的多相位噪声模型

令φk,n和θk,m分别表示第n根发射天线和第m根接收天线在第k时刻的相位噪声。依据文献[11]，相位噪声可由维纳过程描述，且满足如下关系：

φk,n=φk-1,n+uk,n

θk,m=θk-1,m+υk,m

Λ(φk)diag{[e-φk,1,…,e-φk,Nt]T}

Λ(θk)diag{[e-θk,1,…,e-θk,Nr]T}

(2)

则，第k时刻的接收信号yk表示为：

yk=Λ(θk)HΛ(φk)xk+zk

式中，H为MIMO信道矩阵，xk表示第k时刻的发送信号，zk为加性高斯白噪声。

2 LOS MIMO系统的多相位跟踪与补偿

2.1 线性均衡结构下的LOS MIMO系统的多相

位补偿

线性均衡器的代表算法是迫零均衡[13]。对线性均衡结构下的LOS MIMO系统，无相位误差时系统模型如图1所示。

图1 无相位误差的LOS MIMO系统及线性均衡结构Fig.1 A LOS MIMO system without phase noises and linear equalization structure

当LOS MIMO系统中存在多个发送端和多个接收端相位误差时，其模型如图2所示。

图2 含相位误差的LOS MIMO系统Fig.2 A LOS MIMO system with phase noises

定义含发送端相位误差φk的等效发送符号为：

本文提出的线性均衡结构下对相位误差进行补偿的系统模型如图3所示。

图3 线性均衡结构下的LOS MIMO系统的多相位补偿Fig.3 multiple phases compensation for a LOS MIMO system based on linear equalization

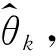
(3)

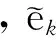
2.2 基于LMS准则的LOS MIMO系统多相位跟踪

首先推导出基于LMS(least mean square)准则的发送端相位误差的跟踪算法，然后推导出基于LMS准则的接收端相位误差的联合跟踪算法。

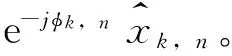
依据LMS准则[15]，可用时刻的样本值

J(φk,n)

(4)

对J(φk,n)，求关于φk,n的一阶偏导，经处理可得：

(5)

式中，lm{·}表示取虚数操作。由LMS准则[15]，可得到第n个发送端相位误差的迭代表达式为：

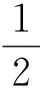
(6)

(7)

定义接收端相位误差θk的跟踪系统的均方误差为：

E {‖WΛ(-θk)yk-Λ(φk + 1)xk‖2}=

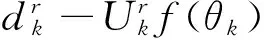
(8)

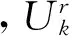
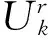
(9)

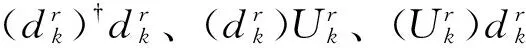
(10)

J(θk)对θk的一阶偏导可表示为

(11)

代入公式(11)，进一步可得

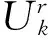
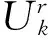
(12)

由LMS准则[15]，可得到接收端多个相位的迭代表达式为

(13)

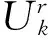
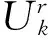
(14)

2.3 LOS MIMO系统多相位跟踪与补偿算法

将多相位跟踪和补偿过程相结合，得到LOS MIMO系统的多相位跟踪与补偿算法，记为LMS算法。具体描述如表1。

2.4 算法复杂度分析

本节对提出的LMS多相位跟踪与补偿算法的复杂度进行分析，并与文献[13]提出的基于锁相环(PLL: phase-locked loop)的多相位跟踪与补偿算法进行复杂度对比。

对LMS算法，在每一个抽样时刻，步骤5-10需要进行乘法和加法运算。对PLL算法，由于只进行接收端的多相位跟踪与补偿，因此只有均衡、发送端相位补偿、判决以及发送端相位跟踪4个步骤，分别对应于LMS算法的步骤6、7、8和9。LMS算法和PLL算法所需乘法和加法运算次数的具体描述如表2。由表2可以看出，这两种算法的运算复杂度相差不大。而本文提出的LMS算法对发送端和接收端的相位都能进行跟踪与补偿，从而LMS算法更具优越性。

表1 LMS算法：LOS MIMO系统多相位跟踪与补偿算法Table 1 LMS algorithm: multiple phases tracking and compensation algorithm for LOS MIMO systems

表2 LMS和PLL算法的运算复杂度比较Table 2 Computational complexity comparison with LMS and PLL

3 仿真结果与分析

考虑一个载频为fc=17 GHz、带宽为1/Ts=50 MHz的MIMO微波系统[16]。系统采用4×4双极化天线系统，交叉极化差别XPD=30 dB，天线间距为d=3 cm，传输距离D=5 km。设每根天线的相位噪声的双边带3 dB带宽为η=80 Hz，且在[0, 2π]间服从均匀分布。发射天线的总发射功率为1 W，接收端SNR定义为平均每根接收天线的信号能量与噪声方差之比。符号帧的长度设为1 024，Monte-Carlo仿真次数为500。将本文提出的LMS算法与文献[13]提出的PLL算法做比较。作为相位跟踪性能的基准，没有相位噪声情况下迫零均衡的仿真结果用“no PHN”表示。

图4为两种算法情形下的多相位跟踪性能。 发送端和接收端天线均采用不同的振荡器时(图4用“Tx-ind, Rx-ind”表示；接收端天线采用相同的振荡器而发送端天线采用不同的振荡器用“Tx-ind, Rx-com”表示。从图4的结果可以看出，当发送端或接收端配置不同的振荡器时，本文提出的LMS算法的误符号率(SER: Symbol Error Rate)比PLL算法低，说明LMS算法具有更好的相位跟踪性能。而发送端和接收端配置不同的振荡器更符合实际应用要求。特别在发送端和接收端均配置不同的振荡器时，PLL算法出现很明显的错误平层。由此可见，LMS算法更具有实用性。

图4 不同振荡器配置下的误符号率Fig.4 SER under different oscillator configurations

图5给出了LMS算法和PLL算法在不同的相位噪声带宽情况下误符号率性能。可以看出，相位噪声的带宽越大，误符号率越大。但随着信噪比的增加，采用LMS算法进行跟踪与补偿后系统的误符号率迅速降低，明显低于PLL算法。

图5 不同相位噪声带宽下的误符号率Fig.5 SER under different bandwidth of phase noise

图6给出了LMS算法和PLL算法在不同的QAM调制阶数下误符号率性能。可以看出，调制阶数越低(4 QAM)，系统的误符号率越小。在相同的调制方式下，采用LMS算法进行跟踪与补偿后系统的误符号率远小于PLL算法。

图6 不同QAM调制阶数下的误符号率Fig.6 SER under different QAM modulation orders

图7给出了LMS算法在采用不同的迭代步长时系统的误符号率性能。结果表明：在中信噪比区间(20～24 dB)时，迭代步长越小，误符号率越低，LMS算法对相位噪声的跟踪性能越好。而随着信噪比的不断增加，不同迭代步长的跟踪性能趋于一致，说明在高信噪比情况下LMS算法对迭代步长的变化具有一定的鲁棒性。

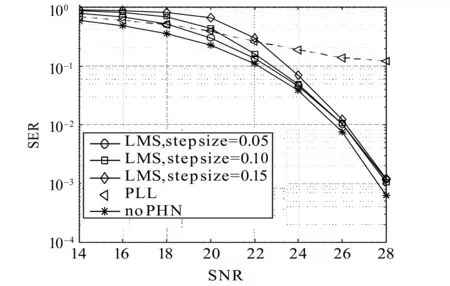
图7 不同迭代步长下的误符号率Fig.7 SER under different step sizes

4 结 语

针对LOS MIMO系统中分布式天线多个发送端和多个接收端相位噪声对系统性能的影响问题，本文首先基于LMS准则从理论上推导出发送端和接收端相位噪声的跟踪算法，并基于线性均衡提出多相位补偿的系统模型；然后，运用该算法进行仿真计算，分析了在不同发送端和接收端振荡器的配置、相位噪声带宽、调制阶数、迭代步长时的系统误符号率性能。同时，与锁相环的多相位跟踪算法(PLL)进行比较，结果表明：在LOS MIMO系统中采用本文提出的LMS算法，其误符号率明显低于PLL算法。特别是在发送端和接收端均配置不同的振荡器时以及高信噪比条件下，LMS算法表现出了优良的相位跟踪与补偿能力，能有效降低系统的误符号率。因此，该算法适用于平坦信道下的LOS MIMO系统，且其解决了LOS MIMO系统中分布式天线多个发送端相位噪声和多个接收端相位噪声的跟踪与补偿问题，具有实际应用价值。下一步，我们将研究频率选择性信道下的LOS MIMO系统的多相位跟踪与补偿算法。

[1] AGIWAL M, ROY A, SAXENA N. Next generation 5G wireless networks: a comprehensive survey[J]. IEEE Communications Surveys & Tutorials, 2016, 18(3):1617-1655.

[2] GE X H, CHENG H, GUIZANI M, et al. 5G wireless backhaul networks: challenges and research advances[J]. IEEE Network, 2014, 28(6): 6-11.

[3] DURISI G, TARABLE A, CAMARDA C, et al. Capacity bounds for MIMO microwave backhaul links affected by phase noise [J]. IEEE Transactions on Communications, 2014, 62(3):920-929.

[4] ABBAS H, HAMDI K. Full duplex relay in millimeter wave backhaul links[C]∥IEEE Wireless Communications and Networking Conference, Doha, Qatar, 2016 : 1-6.

[5] PAULRAJ A J, GORE D, NABAR R U, et al. An overview of MIMO communications-a key to gigabit wireless [J]. Proceedings of the IEEE, 2004, 92(2):198-218.

[6] YANG Y Y, CHU Q X, MAO C X. Multiband MIMO antenna for GSM, DCS, and LTE indoor applications[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15: 1573-1576.

[7] BOHAGEN F, ORTEN P, OIEN G. Design of optimal high-rank line-of-sight MIMO channels [J]. IEEE Transactions on Wireless Communications, 2007, 6(4):1420-1425.

[8] 周冬跃, 胡斌杰. 一种空间复用MIMO-OFDM联合量化反馈预编码[J]. 中山大学学报(自然科学版), 2013,52(5): 39-44.

ZHOU D Y, HU B J. A integrated quantified feedback precoding for spatial multiplexing MIMO-OFDM[J]. Acta Scientiarum Naturalium Universitaties Sunyatseni, 2013, 52(5):39-44.

[9] BAO L, OLSSON B E. Methods and measurements of channel phase difference in 2×2 microwave LOS-MIMO systems[C]∥IEEE International Conference on Communications, London, UK, 2015:1358-1363.

[10] DURISI G, TARABLE A, KOCH T. On the multiplexing gain of MIMO microwave backhaul links affected by phase noise [C]∥ IEEE International Conference on Communications, Budapest, Hungary, 2013:3209-3214.

[11] MATHECKEN P, RIIHONEN T, WERNER S, et al. Performance analysis of OFDM with wiener phase noise and frequency selective fading channel [J]. IEEE Transactions on Communications, 2011, 59(5):1321-1331.

[12] MINN H, AL-DHAHIR N, LI Y. Optimal training signals for MIMO OFDM channel estimation in the presence of frequency offset and phase noise [J]. IEEE Transactions on Communications, 2006, 54(10):1754-1759.

[13] HAELSIG T, LANKL B. Performance evaluation of LOS MIMO systems under the influence of phase noise [C]∥International ITG Workshop on Smart Antennas, Ilmenau, Germany, 2015: 1-5.

[14] BØHAGEN F. Modeling, characterization and design of line-of-sight wireless MIMO channels[D]. The Oslo State University, 2007.

[15] SAYED A H. Adaptive filters [M]. A John Wiley & Sons Inc, Publication, 2011.

[16] INGASON T, LIU H, COLDREY M, et al. Impact of frequency selective channels on a line-of-sight MIMO microwave radio link [C]∥ Proceedings of Vehicular Technology Conference, Ottawa, Canada, 2010:1-5.

[17] MOON, TODD K S, WYNN C. Mathematical methods and algorithms for signal processing[M]. Prentice Hall Inc, 2000.

MultiplephasestrackingandcompensationforLOSMIMOsystems

LUOLiping1,ZHOUJingrong2,CHENHaiqiang3

(1. School of Information Science and Engineering, Guangxi University for Nationalities, Nanning 530006, China;2.School of Electronics and Information Technology, Sun Yat-sen University, Guangzhou 510275, China;3.School of Computer, Electronics and Information, Guangxi University, Nanning 530004, China)

Aiming at the multiple phase noises in distributed transmitter and receiver antennas of LOS MIMO systems, a tracking and compensation algorithm for multiple phases based on LMS criterion and linear equalization is proposed. The symbol error rate (SER) performance is analyzed by simulations under various oscillator configurations, phase noise bandwidth, modulation orders and step sizes. Then, compared with the existed algorithm based on phase-locked loop (PLL), the simulation results show that the SER performance of the LMS algorithm is superior to the PLL algorithm. The proposed LMS algorithm can reduce the SER of LOS MIMO systems more efficiently, thus is more practicable than the PLL algorithm.

LOS MIMO systems; LMS criterion; linear equalization; multiple phase noises; tracking and compensation

TN911.23

A

0529-6579(2017)05-0149-07

10.13471/j.cnki.acta.snus.2017.05.019

2016-12-19

国家自然科学基金(61362010)；广西自然科学基金(2016GXNSFAA380091)；广西高等学校科学研究项目(2013YB073)

罗丽平(1980年生)，女；研究方向认知无线电；E-mail: 78122732@qq.com