一类免疫缺陷病毒传播的非线性动力学系统

冯依虎，陈贤峰，莫嘉琪

(1. 亳州学院电子与信息工程系，安徽 亳州 236800；2. 上海交通大学数学科学学院，上海 200240；3. 安徽师范大学数学系，安徽 芜湖 241003)

一类免疫缺陷病毒传播的非线性动力学系统

冯依虎1，陈贤峰2，莫嘉琪3

(1. 亳州学院电子与信息工程系，安徽 亳州 236800；2. 上海交通大学数学科学学院，上海 200240；3. 安徽师范大学数学系，安徽 芜湖 241003)

研究了人体免疫缺陷病毒(HIV)传播的动力学系统，描述了流行性传染病区域的人群传播规律，提出了一类更广泛的HIV传播的动力学系统。首先，利用泛函广义变分迭代方法对一类艾滋病的传播动力学非线性系统求得到了近似解的迭代序列，并叙述了它的一致收敛性。通过举例, 较简单地得到各次近似解。最后对HIV传播的动力学系统的解作了定量、定性方面的论述和展望。

变分；艾滋病；非线性

流行性传染病的传播，特别是艾滋病等这类人体免疫缺陷病毒(HIV)的传播是生态学界、医学界十分重视的一个研究方面。它对人类健康带来严重的威胁。对于HIV传播的研究，起初只局限于用一些观察的数据来作为分析和推断的依据。这不能完全反映其的本质。当前对艾滋病等这类人体免疫缺陷病毒的传播的探讨，在国际学术界已经将它重点归化为动力学的方法[1-3]。即建立反映其基本现象的微分系统, 并用数学的解析方法求模型的近似解。然后将其研究结果与实际观察作依据，从生态学、医学、数学等交叉学科的理论和方法来研究它的动态规律。本文是以一个非线性动力学HIV传播模型为基础，利用数学中的解析理论工具来研究这类人体免疫缺陷病毒的传播。非线性问题在学术界中是一个极为关注的研究对象。一些科研工作者做了很多工作[4-9]。提出了许多可行的近似方法。作者等也研究了一些非线性问题[10-19]。本文是利用一个简单、有效的泛函广义变分方法研究人体免疫缺陷病毒传播的传染人群中非线性微分系统的模型[1]。

1 免疫缺陷病毒的传播动力学微分系统

讨论如下更广泛的一类人体免疫缺陷病毒的传播人群的生态动力学微分系统的模型：

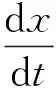
(1)

dx+e-f2(x,y)

(2)

其中x(t)表示在HIV 传播区域内的感染者人数，y(t)为易感者人数，t为时间，e≥0为易感者的出生率，a,b,c,d为常数。在系统(1)-(2)中，a(x+y)y项表示感染者与易感者因“交感”而造成的患者的增加速度，-bx项表示由于患者死亡而引起的患者的减少速度，-a(x+y)x项表示感染者与易感者“交感”易感者变为患者后使得易感者减少的速度， -cx2y项表示采取一般的防疫措施后使得易感者减少的速度，f1(x,y)项为由于其它因素的干扰使得感者增加的速度，-f2(x,y)项为采取更特殊防疫措施后使得易感者减少的速度，不妨设fi(i=1,2)为充分光滑的有界函数。系统(1)-(2)是一个在患区人群的HIV传播的生态动力学模型。我们来构造模型(1)-(2)近似解的表达式，并从得到的表示式来研究HIV的传播性态和规律。

首先考虑系统(1)-(2)的一类简化问题

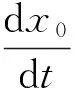
(3)

(4)

由系统(3)-(4)，不难得到它的解

X0(t)=C0exp(-bt)

(5)

(6)

式中X0由式(5)表示。而C0和D0为任意常数，它们可由系统的初始状态来决定。为了方便，我们取无量纲参数C0=1,D0=0(下同)。因此由式(5)-(6), 得

X0(t)=exp(-bt)

(7)

Y0(t)=

(8)

2 广义泛函变分迭代

现讨论HIV生态动力学非线性微分系统(1)-(2)的解。显然, 非线性微分系统一般是不能用有限项的初等函数来得到其精确解的。为此下面用泛函广义变分迭代方法来求其近似解。

引入一组泛函Fi(i=1,2):

F1[x]=x-

(9)

(10)

取泛函(9)-(10)的变分, 并令其为零:

δF1=δ,

于是

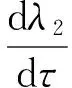
故有

(11)

由关系式(9)-(10), 我们构造如下一组广义变分迭代式:

(12)

(13)

因此, 当选定一组初始迭代函数(x0,y0)后, 我们可以由广义变分迭代式(12)-(13)决定函数序列{xn(t)},{yn(t)}。

事实上, 选取初始迭代函数(x0,y0)为由式(7)-(8)表示的一组函数(X0,Y0)。即

x0(t)=exp(-bt)

(14)

y0(t)=

(15)

由广义变分迭代式(12)-(13)和初始迭代函数(14)-(15), 可以得到生态动力学非线性微分系统(1)-(2)的一次近似解(x1,y1):

[-a(exp(-bt)+y0)y0-f1(exp(-bτ),y0)]dτ

(16)

(17)

其中y0由式(15)表示。

依次地, 生态动力学非线性微分系统(1)-(2)的二次近似解(x2,y2)为

(18)

(19)

其中(x1,y1)由式(16)-(17)表示。

同样, 可依次地得到HIV生态动力学非线性微分系统(1)-(2)的更高次的表示式(xm,ym),m=3,4,…。

3 举 例

为了简单起见, 设人体免疫缺陷病毒的传播人群的生态动力学微分系统的模型(1)-(2)中的参数为无量纲数:a=b=c=d=1,e=0, 而扰动函数分别为f1=siny,f2=cosx, 这时HIV生态动力学微分系统的模型(1)-(2)为

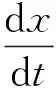
(20)

(21)

由式(14)-(15), 广义变分迭代的初始函数为

x0(t)=exp(-t)

(22)

(23)

由式(16)-(17), HIV生态动力学非线性微分系统(1)-(2)的一次近似解(x1,y1)为

[(exp(-τ)+y0)y0+siny0]dτ

(24)

(25)

其中y0由式(23)表示。

由式(18)-(19), HIV生态动力学非线性微分系统(1)-(2)的二次近似解(x2,y2)为

y2(t)=y1(t)-

其中(x1,y1)由式(24)-(25)表示。

可以继续得到人体免疫缺陷病毒的传播人群的生态动力学微分系统的模型(20)-(21)的更高次近似解。

4 结 论

1) 由人体免疫缺陷病毒的传播人群的生态动力学微分系统的模型(1)-(2)的近似解的解析展开式，我们能够研究HIV的传播性态和规律，并利用微分系统的模型参数来发现和控制人体免疫缺陷病毒的传播区域内在不同时间内的感染者人数和易感者人数和采取措施来控制感染者人数和易感者人数。

2) 从数学观点来看，广义变分迭代法是一个解析的方法。它不同于通常的数值求解法，更不是简单的模拟。本方法得到的解的近似解析表示式，还可进行解析运算。例如可以由得到的近似解析表示式进行定性和定量方面的研究。诸如，用微分的方法算出感染者和易感染者数量的变化速度、画出在不同时间的数量变化曲线，并发现其规律和预报感染者和易感染者在相关时期内的数量和发展趋向的规律等等。

[1] GRIFFITHS J, LO WRIE D, WILLIAMS J An age-structured model for the AIDS epidemic [J]. European J Operational Research, 2000, 124(1): 1-24.

[2] HYMAN J M, LI J, STANLEY E A. The differential infectivity and staged progression models for the transmission of HIV [J]. Mathematical Biosciences, 1999, 155(1): 77-109.

[3] LIU M X, RUAN Y H, HAN L T, et al. The summary of dynamic models for HIV transmission [J]. J Biomathematics, 2004, 19(5): 551-560.

[4] de JAGER E M, JIANG F. The theory of singular perturbation [M]. Amsterdam: North- Holland Publishing Co,1996.

[5] BARBU L, MOROSANU G. Singularly perturbed boundary-value problems [M]. Basel: Birkhauserm Verlag AG, 2007.

[6] D’APRILE T, PISTOIA A. On the existence of some new positive interior spike solutions to a semilinear Nuumann problem [J]. J Differ Eqns, 2010, 248(3): 556-573.

[7] EI SHIN-ICHIRO, MATUZAWA H. The motion of a transition layer for a bistable reaction diffusion equation with heterogeneous environment [J]. Discrete Contin Dyn Syst, 2010, 26(3): 910-921.

[8] SUZUKI R. Asymptotic behavior of solutions of a semilinear heat equation with localized reaction [J]. Adv Differ Eqns, 2010, 15(3/4): 283-314.

[9] DENG S B. Mixed interior and boundary bubbling solutions for Neumann problem in R2 [J]. J Differ Equations, 2012, 253(2): 727-763.

[10] MO J Q. Singular perturbation for a class of nonlinear reaction diffusion systems [J]. Science in China, Ser A, 1989, 32(11): 1306-1315.

[11] MO J Q, LIN W T. Asymptotic solution of activator inhibitor systems for nonlinear reaction diffusion equations [J]. J Sys Sci & Complex, 2008, 20(1): 119-128.

[12] MO J Q. Homotopic mapping solving method for gain fluency of laser pulse amplifier [J]. Science in China, Ser G, 2009, 39(5): 568-661.

[13] MO J Q. Singularly perturbed solution of boundary value problem for nonlinear equations of fourth order with parameters [J]. Adv in Math,2010,39(6): 736-740.

[14] MO J Q, LIN W T. Generalized variation iteration solution of an atmosphere-ocean oscillator model for global climateplexitym [J]. J Sis Sci & Complex, 2011, 24 (2): 271-276.

[15] MO J Q, LIN Y H, LIN W T, et al. Perturbed solving method for interdecadal sea-air oscillator model [J]. Chin Geogr Sci, 2012, 22(1): 42-47.

[16] FENG Y H, MO J Q. The shock asymptotic solutin for nonlinear elliptic equation with two parameters [J]. Math Appl, 2015, 27(3): 579-585.

[17] FENG Y H, LIU S D. Spike layer solutions of some quadratic singular perturbation problems with high-order turning points [J]. Math Appl, 2014, 27(1): 50-55.

[18] 冯依虎, 石兰芳, 汪维刚，等. 一类广义非线性强阻尼扰动发展方程的行波解[J]. 应用数学和力学, 2015, 36(3): 315-324.

FENG Y H, SHI L F, WANG W G, et al. The traveling wave solution for a class of generalized nonlinear strong damping disturbed evolution equations [J]. Appl Math Mech, 2015, 36(3): 315-324.

[19] 冯依虎, 石兰芳, 汪维刚，等. 一类大气尘埃等离子体扩散模型研究[J]. 应用数学和力学, 2015, 36(6): 639-650.

FENG Y H, SHI L F, WANG W G, et al. The study for a class of atomy plasma diffusion model in atmosphere [J]. Appl Math Mech, 2015, 36(6): 639-650.

[20] 何吉欢, 工程和科学计算中的近似非线性分析方法[M]. 郑州：河南科学技术出版社, 2002.

AclassofnonlineardynamicsystemofhumangroupsforHIVtransmission

FENGYihu1,CHENXiangfeng2,MOJiaqi3

(1. Department of electronics and Information Engineering, Bozhou College, Bozhou 236800, China;2. School of Mathematics Sciences, Shanghai Jiaotong University, Shanghai 200240, China;3. Department of Mathematics, Anhui Normal University, Wuhu 241003, China)

A class of dynamic system for the human groups in epidemic contagion region (HIV) transmission is studied. Transmission mode of the human groups in epidemic contagion region is described. Firstly, using the generalized functional variational iteration method for a class of AIDS transmission dynamic system, the approximate iteration sequence is solved. Its uniformly convergent is illustrated. And from an example, any times approximate solutions are obtained. Finally, the quantity and quality of the solution for HIV transmission dynamic system are illustrated and forecasted.

variational; AIDS; nonlinear

O175.14

A

0529-6579(2017)05-0060-04

10.13471/j.cnki.acta.snus.2017.05.008

2016-12-16

国家自然科学基金 (110371248)；安徽省教育厅自然科学重点基金(KJ2015A347)；安徽省高校优秀青年人才支持计划重点项目(gxyqZD2016520)

冯依虎(1982年生)，男；研究方向应用数学；E-mail: fengyihubzsz@163.com

莫嘉琪(1937年生)，男；研究方向：应用数学、数学物理；E-mail: mojiaqi@mail.ahnu.edu.cn