基于多新息最小二乘法的船舶操纵响应模型参数辨识

谢 朔, 初秀民， 柳晨光,2a， 吴 青,2b

(1.国家水运安全工程技术研究中心， 武汉 430063； 2.武汉理工大学 a. 能源与动力工程学院; b. 物流工程学院， 武汉 430063)

基于多新息最小二乘法的船舶操纵响应模型参数辨识

谢 朔1,2a, 初秀民1， 柳晨光1,2a， 吴 青1,2b

(1.国家水运安全工程技术研究中心， 武汉 430063； 2.武汉理工大学 a. 能源与动力工程学院; b. 物流工程学院， 武汉 430063)

提出基于多新息最小二乘法的船舶二阶非线性响应型模型参数辨识方法。在实验室环境下对模型船开展Z形试验，分别应用最小二乘递推法和多新息最小二乘法对试验数据进行参数辨识；用得到的模型分别进行Z形试验预报，比较2种方法的准确性和辨识结果的收敛性。试验结果表明：基于多新息最小二乘法的船舶操纵响应模型参数辨识结果收敛更迅速且精度满足要求。

船舶操纵；响应模型；参数辨识；多新息最小二乘法

Abstract: A parameter identification method for second order nonlinear ship response model is put forward based on the multi-innovation least squeres algorithm. Ordinary recursive least squares algorithm and the proposed MILS (Multi-Innovation Least Square) algorithm are applied respectively in parameter identification with the Z test data of the ship model. The identified parameters are used to do Z test prediction. Prediction accuracy and convergence of identified maneuvering response model parameters from two processes are compared. The comparison proves that identification results based on the MILS algorithm is more accurate and have a higher convergence speed.

Keywords: ship maneuvering; response model; parameter identification; MILS

最小二乘递推法(Recursive Least Square, RL S)作为最小二乘法的改进递推形式，具有辨识精度较高、数据计算量小和简单易用的特点，在船舶模型参数辨识中具有广泛应用。[1-3]文献[4]在船舶航向的广义预测控制中使用最小二乘递推法对船舶响应模型中的参数进行辨识；文献[5]将P型迭代学习率引入到最小二乘递推算法中，并将其应用到船舶一阶和二阶的非线性响应模型中，通过试验验证辨识算法在线辨识的有效性和收敛性。然而，最小二乘递推法因信息获取的限制，辨识精度比最小二乘法低且收敛较慢。对此，丁锋[6]提出多新息最小二乘法(Multi-Innovation Least Square, MILS)，将最小二乘递推算法中每次递推使用的单新息标量扩展为一定长度的多新息向量，从而在保证辨识精度的前提下提高参数在线辨识的收敛速度。文献[7]验证MILS在水下机器人动力学模型参数辨识中的有效性和优越性。

这里针对船舶的二阶非线性响应模型，通过对模型船Z形试验数据进行分析，将多新息最小二乘法应用到船舶操纵模型的参数辨识中，并用建立的响应模型进行Z形试验操纵预报，将结果与最小二乘递推法辨识的结果相对比。

1 船舶操纵响应模型

响应型模型[8]用来描述船舶的操纵运动状态，主要研究艏向角相对于舵角的变化响应关系，是船舶运动控制领域中应用最广泛的数学模型。其数学表达式为

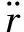
(1)

式(1)中：r为艏向角速度；δ为操舵角；K为增益系数；T1，T2和T3为时间常数。

该模型为船舶操纵响应二阶线性模型，而船舶实际运动比较复杂，用线性模型难以描述其动态过程。若考虑加上非线性项αr3(α为非线性系数)和初始直航所需压舵角δr，则可得到二阶非线性操纵响应模型[9]为

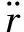
(2)

若考虑船舶操舵的延时特性[10]，则舵机伺服系统的特性方程为

(3)

式(3)中：TE为时间常数；KE为控制增益；δ为实际舵角；δE为输入的舵令。

结合式(2)和式(3)得到考虑舵机伺服特性的船舶操纵响应模型。非线性控制系统常用状态空间模型来描述状态变化，因此该模型可变换为

(4)

则状态方程为

(5)

2 模型参数辨识

最小二乘参数辨识方式可分为连续型和离散型2种。连续逼近需进行积分计算，计算量较大，因此可通过离散化转化为离散逼近来简化。基于多新息最小二乘法的离散参数辨识过程为：

1)非线性模型离散化。

2)从最小二乘递推法出发，结合多新息辨识理论给出基于多新息最小二乘法的船舶二阶非线性响应模型参数辨识方法。

2.1模型离散化

考虑将式(2)离散化为最小二乘回归模型格式，即

Y=φTθ+v

(6)

式(6)中：Y为系统输出向量；v为随机干扰噪声；φT为系统输入输出数据构成的信息向量；θ为待辨识的系统参数向量。

(7)

对式(7)进行前向差分，可得到离散形式为

y(t)-2y(t-1)+y(t-2)=h(y(t-2)-

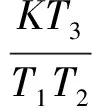
(8)

(9)

由式(9)可将模型化为最小二乘格式，即

(10)

2.2多新息最小二乘参数辨识

针对式(10)，由最小二乘递推算法辨识的流程[11]为

(11)

(12)

式(12)中：p0为>1的常数，一般取106；1n为所有元素为1，长度为n的列向量；I为单位对角矩阵。

为增加旧信息数据的使用频率，提高最小二乘递推法辨识的精度和收敛速度，将式(11)中的新息标量e(t)拓展为长度为p的多新息向量E(p,t)。

(13)

同理，信息向量和输出向量拓展为

(14)

将拓展后的矩阵代入到式(11)中，可得

(15)

于是，最小二乘递推算法可拓展为

(16)

式(16)中对辨识参数矩阵和协方差阵的初值设定同式(12)。综上，使用多新息最小二乘法对船舶操纵模型进行参数辨识的步骤为：

1)使用船舶操纵模型的输入输出数据对式(9)中的输出向量Y(t)和信息向量φ(t)进行赋值。

2)按照式(14)和式(15)扩展出多新息算法所用的输出矩阵Y(p,t)、信息矩阵φ(p,t)和新息矩阵E(p,t)。

3)根据式(16)进行参数估计。

4)在参数矩阵辨识完成后，可求解出模型中的K，T1，T2，T3，α和δr等参数。

结合式(9)，设解算的参数矩阵为

(17)

可得到

(18)

从辨识过程中可看出：当信息长度p=1时，多新息最小二乘法为最小二乘递推算法。前者的优点为：

1)相比经典最小二乘法，由于只使用每次的新息数据对辨识结果进行修正，因此可在较少的计算量下实现在线参数辨识，具有良好的抗干扰能力。

2)相比最小二乘递推法，在使用相同的样本数据时，每次迭代过程中可使用p个新息进行计算，参数收敛速度更快，估计精度更高。

3 试验验证

辨识的有效性体现在辨识结果的准确性和收敛速度2方面。分别使用最小二乘递推法和多新息最小二乘法对船舶二阶非线性响应模型中的K，T1，T2，T3，α和δr等6个参数进行辨识，并利用辨识结果进行船舶操纵预报，最后对预报结果进行对比分析。用操纵预报曲线与实船数据的拟合程度衡量操纵模型的准确性，用辨识过程中参数收敛至稳定值所需的步数衡量辨识的收敛速度。

3.1试验过程

船舶Z形试验数据可为船舶响应模型中的参数辨识提供数据来源，并通过重复摆舵为递推辨识提供足够的持续激励。该试验选用一艘鱼雷艇的缩尺模型船(见图1)作为研究对象。

该模型船具有良好的操舵响应能力，船体上安装有控制电路板和工控机，用以执行Z形试验的程序并记录试验数据。试验验证流程见图2。

图1 模型船

图2 试验验证流程

3.1.1Z形试验

采用20°的Z形试验获取艏向角和舵角的响应数据，试验流程见图3。为保证试验数据的充分性，需至少采集到右舵角出现2次最大值。

3.1.2操纵性预报

为验证辨识结果的准确性，利用所辨识的参数进行Z形试验预报。采用工程上广泛采用的四阶龙格-库塔(Runge-Kutta)法进行船舶响应状态的仿真预报。取式(5)中的状态量作代换，即

(19)

则状态方程表述为

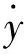
(20)

递推预报公式为

(21)

式(21)中：h为时间间隔；yt为t时刻的预报值；k1，k2与k3，k4分别为时间段开始、中点和结束时的斜率。计算步骤为：

(1)时间段开始时的斜率k1为t时刻状态量的微分，即

k1=f(t,yt)

(22)

(2)时间段中点时的斜率k2与k3为t+h/2时刻状态量的微分，分别采用斜率k1和k2决定y在t+h/2时刻的值，即

(23)

(3)时间段结束时的斜率k4为t+h时刻状态量的微分，其y值用k3决定，即

k4=f(tn+h,yn+hk3)

(24)

由式(21)～式(24)组成操纵预报的递推公式。该方法是一种高精度的单步算法，常用于数值求解高阶微分方程，具有易收敛、稳定的特点。[12]操纵预报解算流程见图4。

图4 操纵预报解算流程

该算法在MATLAB平台上实现，其控制序列由Z形试验获取的舵角数据得到，并使用ode45函数解算各步的状态量。ode45所使用的状态方程为式(5)。

3.2试验结果及分析

3.2.1试验结果

试验时采样周期h=0.25 s，试验过程中同时记录模型船舵角离散数δ(t)和艏向角离散数据y(t)。

3.2.1.1 参数辨识结果

分别采用最小二乘递推法和多新息最小二乘法对二阶非线性响应模型进行参数辨识。由于多新息最小二乘法辨识结果的准确性和收敛性与所取新息长度p有关，因此分别取信息长度p=40，45和50下的多新息最小二乘法辨识的结果进行对比(见表1)。

3.2.1.2 操纵性预报结果

分别选取最小二乘递推法和多新息最小二乘法辨识的结果进行预报。航向预报结果见图5。

3.2.2结果分析

对于操纵预报的结果，从辨识的准确性和收敛性2个方面进行分析：使用拟合度评价函数的值度量辨识算法的准确性；使用辨识结果开始收敛所需递推的步数度量辨识算法的收敛性。

表1 辨识结果

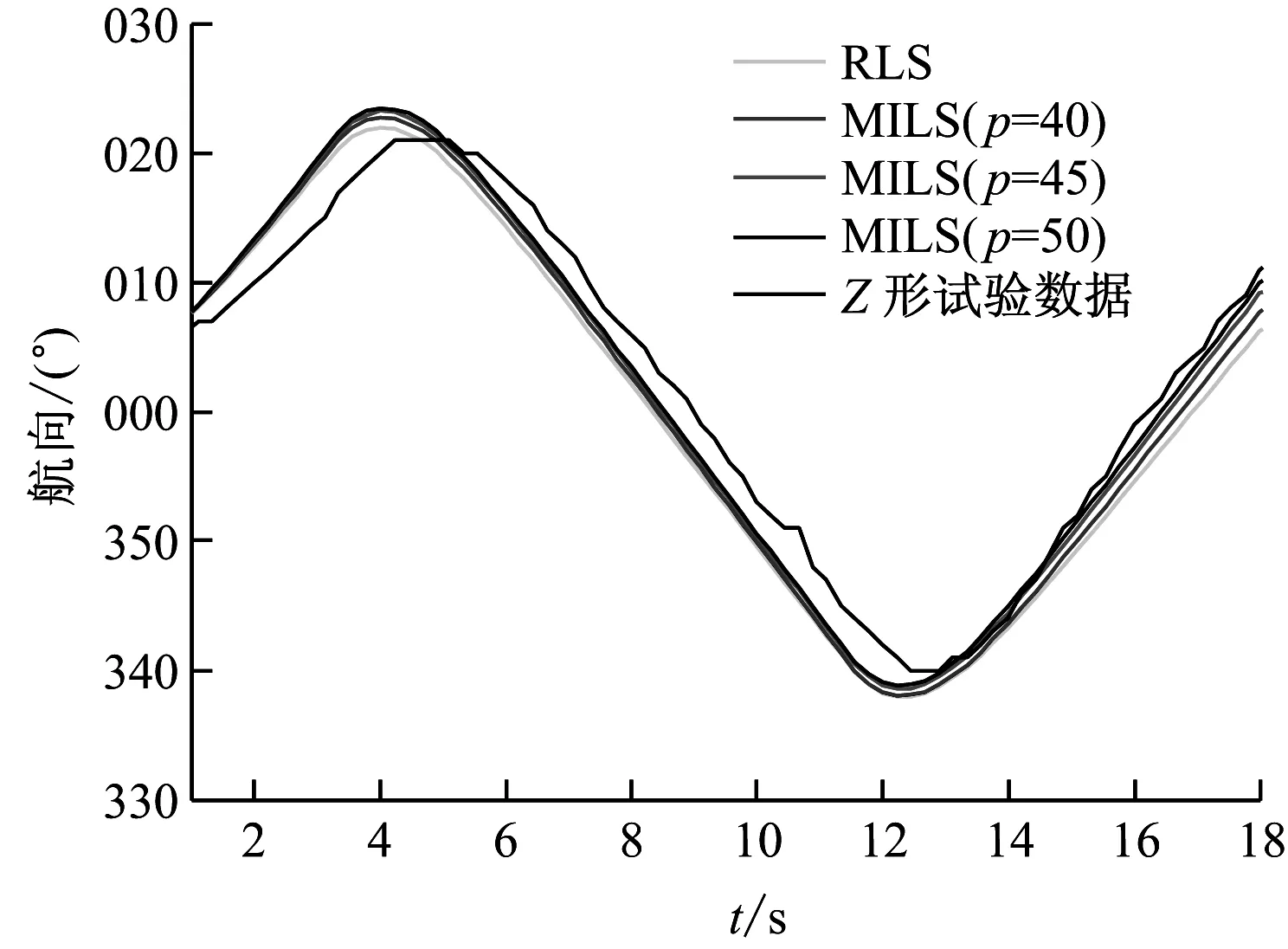
图5 航向预报结果

3.2.2.1 辨识准确性

从图5中可看出，最小二乘递推法和多新息最小二乘法所预报的航向与试验的结果都较为吻合，辨识的准确性需进行量化对比。由于最小二乘法是通过最小化误差平方和来求取拟合函数的方法，因此选取均方误差作为拟合度评价函数。

(25)

式(25)中：n为离散数据的个数；Ψ(t)为t时刻预报解算的艏向角；Ψ0(t)为t时刻Z形试验的艏向角。其误差结果见表2。

表2 误差结果

从表2中可看出：多新息最小二乘法辨识结果的预报误差均比最小二乘递推法小，且均方误差均在10(°)2以下，满足辨识精度要求；随着信息长度p增加，多新息最小二乘法辨识结果的预报误差逐渐减小，辨识精确度越来越高。

3.2.2.2 辨识结果收敛性

分别将最小二乘递推法与p=40，45和50下多新息最小二乘法每次递推修正的各参数K，T1，T2，T3，α，δr的结果记录下来，并进行对比，结果见图6。图6中，横坐标表示递推的步数N，纵坐标表示各参数每步的计算值，可看出各参数收敛时需经过的递推步数，具体见表3。

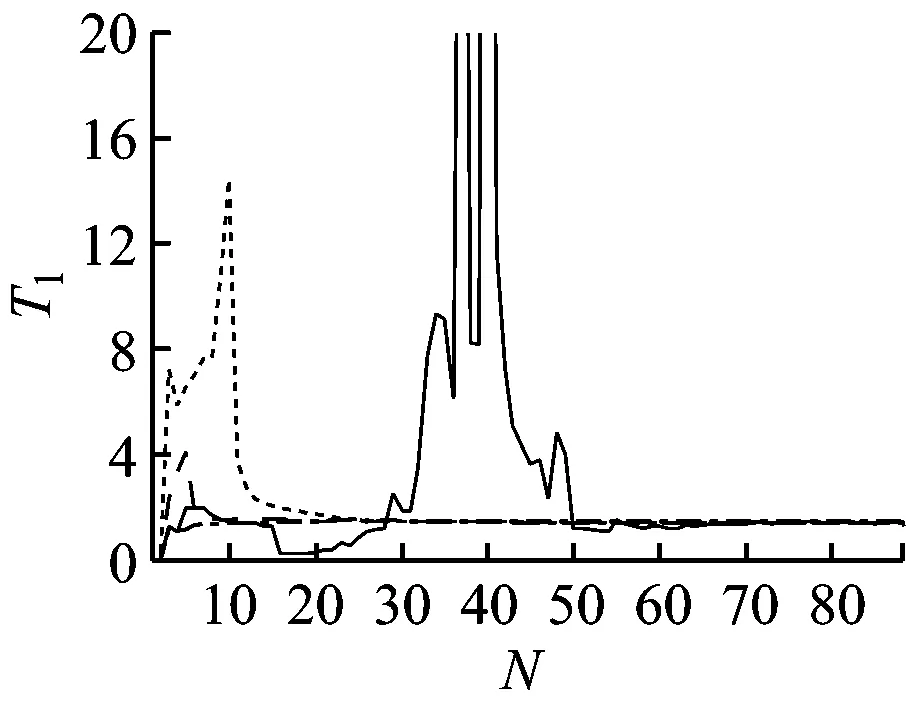
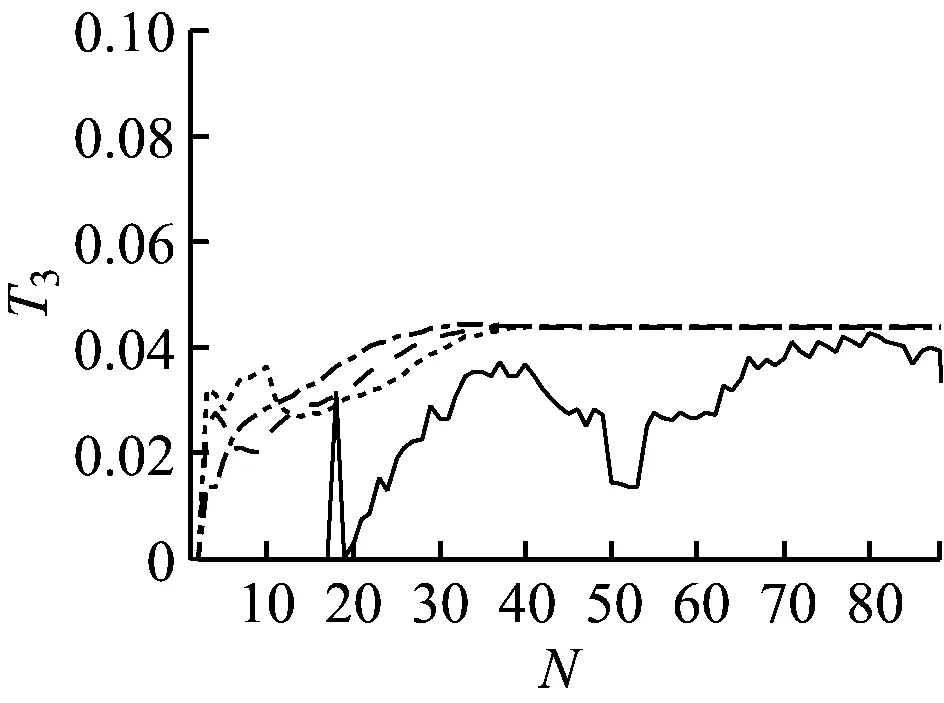
图6 参数辨识结果

表3中，NK，NT1，NT2，NT3，Na，Nδr分别表示K，T1，T2，T3，α，δr等6个参数收敛至稳定值所需的递推步数。可看出：

1)多新息最小二乘法辨识的各参数收敛的速度明显比最小二乘递推法快，且在前几步递推中，多新息最小二乘法辨识中的参数修正很稳定，其相对于真实值的误差下降十分迅速；而最小二乘递推法辨识参数在后期出现扰动，这对带有不良数据的在线辨识是不利的。

2)多新息最小二乘法的信息长度p越大，算法的收敛速度越快。

4 结束语

本文针对船舶运动响应模型参数辨识问题，将多新息最小二乘法引入到船舶二阶非线性响应模型的参数辨识中，并采用最小二乘递推法进行对比验证。结果表明，多新息最小二乘法的收敛速度更快且精度满足要求。因此，基于多新息最小二乘法辨识的船舶响应模型参数更接近真实值，能更准确地描述船舶运动的动态特性，且该方法在实时性方面继承了最小二乘递推法的优点，在未来的自适应控制中可考虑使用该方法实现船舶运动响应模型的自主辨识。

[1] 王德普. 船舶操纵性模型辨识[J]. 沈阳工业学院学报, 1998, 17(4): 13-16.

[2] 张显库, 金一丞. 汽车运输船的响应型非线性数学模型[J]. 哈尔滨工程大学学报, 2007, 28(5): 487-490.

[3] 张心光, 邹早建. 基于支持向量回归机的船舶操纵响应模型辨识[J]. 上海交通大学学报, 2011, 45(4): 501-504.

[4] QIN Y, MA Y. Parametric Identification of Ship's Maneuvering Motion Based on Improved Least Square Method[C]//International Conference on Mechatronics, 2014.

[5] HU Y, XU S. A Direct Generalized Predictive Controller for Ship Course Keeping[C]//Conference on Control & Automation, 2007： 1-4.

[6] 丁锋. 系统辨识 (6): 多新息辨识理论与方法[J]. 南京信息工程大学学报(自然科学版), 2012, 4(1): 1-28.

[7] 朱胜庭, 朱大奇, 邓志刚. 多新息最小二乘法辨识水下机器人动力学模型[J]. 系统仿真学报, 2013, 25(6): 1399-1404.

[8] NOMOTO K，TAGUCHI K， HONDA K， et al. On the Steering Qualities of Ships[J]. International Shipbuilding Progress, 1957, 4(35):354-370.

[9] 王春园. 模型船的数学模型辨识[D]. 大连：大连海事大学, 2012.

[10] 袁雷, 吴汉松. 船舶航向控制的多滑模鲁棒自适应设计[J]. 控制理论与应用, 2010, 27(12): 1618-1622.

[11] WALTER E, PRONZATO L. Identification of Parametric Models[M]. Berlin: Springer, 2010.

[12] BUTCHER J C. The Numerical Analysis of Ordinary Differential Equations: Runge-Kutta and General Linear Methods[M]. New York: Wiley-Interscience, 1987: 102-121.

ParameterIdentificationofShipManeuveringResponseModelBasedonMulti-InnovationLeastSquaresAlgorithm

XIEShuo1,2a,CHUXiumin1,LIUChenguang1,2a,WUQing1,2b

(1. Engineering Research Center for Transportation Safe, Wuhan 430063, China; 2a. School of Energy and Power Engineering; 2b. School of Logistics Engineering, Wuhan University of Technology, Wuhan 430063, China;)

U661.33

A

2016-10-25

交通运输部科技成果推广项目(2015326548030)；湖北省自然科学基金重点项目(2015CFA111)

谢 朔(1993—)，男，湖北天门人，硕士生，主要研究方向为船舶智能化。E-mail: xieshuo@whut.edu.cn 初秀民(1969—)，男，吉林通化人，研究员，博士生导师，主要研究方向为水上交通安全状态感知。E-mail: chuxm@whut.edu.cn

1000-4653(2017)01-0073-06