一个单服务器辅助的高效n取k茫然传输协议

赵圣楠 蒋 瀚 魏晓超 柯俊明 赵明昊

1(山东大学计算机科学与技术学院 济南 250101) 2(山东师范大学信息科学与工程学院 济南 250358) (yucheng＿zhao@163．com)

2017-06-11；

2017-07-29

国家自然科学基金项目(61572294)；国家自然科学基金青年科学基金项目(61602287)；国家自然科学基金重点项目(61632020)；山东大学基本科研业务费专项资金项目(2017JC019) This work was supported by the National Natural Science Foundation of China (61572294), the National Natural Science Foundation of China for Young Scientists (61602287), the Key Program of the National Natural Science Foundation of China (61632020), and the Fundamental Research Funds of Shandong University (2017JC019).

蒋瀚(jianghan@sdu.edu.cn)

一个单服务器辅助的高效n取k茫然传输协议

赵圣楠1蒋 瀚1魏晓超2柯俊明1赵明昊1

1(山东大学计算机科学与技术学院 济南 250101)2(山东师范大学信息科学与工程学院 济南 250358) (yucheng＿zhao@163．com)

茫然传输；外包计算；判定性Diffie-Hellamn假设；半诚实模型；安全多方计算

外包计算作为当今新型的计算模式，日渐受到研究者和企业界的关注.物联网、移动计算、无线传感器网络等技术的兴起和普及极大地方便了我们的生活、沟通与信息获取，但是出于效率和成本等因素的考虑，这类设备通常采用轻量级硬件架构，计算和存储能力受到极大的限制.

云计算的兴起为能力受限的移动设备提供了完美的后端支持.当前的服务计算架构中，一方面云服务器为移动设备提供视频分发、数据分析以及广告推送等服务；另一方面移动设备会将复杂的计算任务外包到云端，云端完成计算任务后将计算结果返回给移动设备.云计算和外包计算模式，极大地丰富了移动计算的内容[1].

出于安全和隐私性考虑，移动设备(如手机客户端、RFID芯片、传感器网络节点等)之间往往需要执行认证和加密等多种密码学原语，其中以公钥密码原语居多.在公钥密码中通常需要涉及大量的群上的指数运算，这对于移动设备来说是极大的负担.目前虽然可以设计专用的嵌入式芯片来高速实现密码原语操作[2-3]，但这一定程度上会增加设备成本.因此，目前一个很理想的解决方案是将公钥加密方案的部分复杂运算外包到云端来进行.

茫然传输(oblivious transfer, OT)是密码学中一个基础工具.传统的茫然传输协议中有2个参与方：发送方S和接收方R，协议的目的是让接收方从发送方的输入中获取自己选择的输入，且满足：1)发送方不知道接收方的选择；2)接收方只能获得自己选择的输入且无法获得额外的输入信息.茫然传输在隐私保护的数据查询、安全多方计算等多个领域有重要应用[4].

1 相关工作和主要结论

1.1相关工作

双向OT使得每个参与方都兼有发送者和接受者的双重身份，该原语可以大大降低基于cut-and-choose的安全多方计算协议的轮复杂度.Zhao等人[27]和Wei等人[28]在双向OT领域做出了创举性的研究；抗量子OT有文献[29-30]等.

密码学原语的部分外包.通常来讲群指数运算是密码算法中最为耗时的运算.Dijk等人[31]首先考虑将指数运算外包给一个不可信的服务器；Ma等人[32]考虑了将指数操作外包到2个非合谋的不可信服务器；Hohenberger等人[33]和Chen等人[34]将变基和变幂的指数算法外包到(双服务器模型下的)单一恶意服务器，即要求2个服务器中仅有一个服务器为恶意的，且不与另一个诚实服务器合谋.文献[34]同时考虑了安全与高效的并发指数(simultaneous exponentiations)操作外包；Wang等人[35]实现了一个单一非可信服务器模型下的指数运算外包方案；Chevalier等人[36]对该方案做了细致的密码学分析，并给出了一个优化的构造方案；Tsang等人[37]首先考虑了以批量的方式将椭圆曲线上的点对运算(pairing)外包到云服务器上来实现；Canard等人[38]给出了一个更为高效的安全点对运算外包方案；Xu等人[39]考虑将复杂运算外包到计算服务器P，并将外包计算结果的正确性验证外包到验证服务器V，其隐私性保证不向计算服务器和验证服务器泄漏数据信息；Gennaro等人[40]首次提出非交互的可验证外包计算；Carter等人[41]将基于cut-and-choose安全多方计算中的混乱电路求值外包给云服务器来做；文献[42-43]则将混乱电路的生产任务外包给移动设备；服务器辅助的通用两方计算协议方案有文献[44-45]等.和本文工作最为相关的是Wei等人[45]提出的云服务器辅助茫然传输协议，该方案涉及2个非合谋的服务器且在半诚实模型下达到可证明安全.

1.2本文工作

我们设计了一种新的基于单个云服务器的k-out-of-nOT协议.文献[45]将群指数运算外包到2个诚实但好奇且相互独立的云服务器上，云服务器诚实但好奇的性质说明该协议是在半诚实模型下执行，云服务器之间相互独立意味着2个云服务器之间不能合谋.该方案虽然降低了通信双方的本地计算量，却存在2个明显的弊端：首先外包计算目前仍需要支付大量的费用，将群指数运算外包到2个云服务器更是要有足够的经济支撑，出于预算考虑在某些应用场景下不得不放弃使用该协议；再者，2个云服务器不能合谋的安全假设过于理想，2个云服务器一旦合谋就可以知道接收方的输入选择，或者云服务器与接收方合谋来获得发送方的全部输入，这样协议的安全性就完全得不到保证.因此，我们希望在保证安全和效率的基础上将云服务器的个数减少至一个，从而避免2个云服务器合谋的严重弊端.我们具体的贡献有3方面：

1) 将RAND 函数的计算过程分散到发送方和云服务器，并以一种新的形式嵌入发送方的输入值.

2) 将群指数运算外包到一个云服务器，设计出基于单个云辅助的高效n取k茫然传输协议，该协议是安全三方计算的实例，并依据诚实方大多数原则证明其安全性.

3) 相对于其他基于DDH假设的n取k茫然传输协议，我们将协议的计算和通信复杂度降至O(n)量级.

2 基本知识和安全定义

2.1DH元组

令G为一个以g为生成元的q阶群，q为素数.将形如(gα,gβ,gαβ)的三元组称为DH元组，这里的α,β随机取自q.也就是说，对于任意群G上的三元组(gα,gβ,gγ)，α,β,γ∈q，若γ≡α×β(modq)则称该元组为DH元组，否则为非DH元组.

2.2DDH假设

DDH问题定义：给定上述群G上的四元组(g,gα,gβ,gγ)，α,β,γ∈q，判定γ≡α×β(modq)是否成立.若等式成立，由于该元组的第1个元素为生成元，所以该四元组与上述所定义的三元组构成的DH元组并不矛盾，四元组(g,gα,gβ,gγ)仍称为DH元组.将生成元看作一个公开参数，那么任意三元组都可以写成四元组的形式，因此从现在起所有的DH元组均默认为四元组.那么，DDH假设是指下述2种总体分布是计算不可区分的：

1)X1=(g,ga,gb,ga b)，这里a,b∈q；

2)X2=(g,ga,gb,gc)，这里a,b∈q，但ab≠c.

2.3RAND函数

RAND函数定义在群G构成的DH元组(w,x,y,z)上，w,x,y,z∈G，函数RAND(w,x,y,z)=(u,v)，其中u=ws×yt，v=xs×zt，这里s,t∈q.注意，对任意的DH元组(w,x,y,z)，必然存在a∈q，满足y=wa,z=xa.因此，RAND函数有性质：

1) 如果(w,x,y,z)是DH元组且满足y=wa，z=xa，那么对于u,v←RAND(w,x,y,z)满足ua=v.

2) 如果(w,x,y,z)为非DH元组，那么(w,x,y,z,RAND(w,x,y,z))，(w,x,y,z,ga,gb)在分布上是等价的，这里α,β随机取自q.

显然，RAND函数的计算过程能够分为ws，yt，xs和zt这4个部分，我们可以将这4个部分分发给不同参与方，然后联合计算出函数值.

2.4安全性定义

本文中我们考虑基于单服务器辅助的n取k茫然传输协议.为了定义基于云服务器外包协议的安全性，我们参考了文献[45-46]中提出的安全多方计算在外包环境中安全定义.在文献[45]中协议是基于2个相互独立的云服务器，我们的协议将云服务器个数减少为一个，相当于发送方在协议执行过程中扮演了原方案中一个云服务器的角色.协议共涉及3个参与方，因此我们将协议的执行过程看作是安全三方计算的实例，遵循诚安全多方计算里诚实方大多数原则，即在该协议中敌手只能腐化至多一个参与方，因此不考虑任意2方合谋的情况.我们设计的协议中，仍然定义云服务器是诚实但好奇的，且与协议双方保持独立.诚实但好奇意味着云服务器不仅根据指令诚实地执行协议的每一步操作，并且想要依据接收到的消息副本来试图获得发送方或接收方的输入.但云服务器不能与发送方或接收方中的任意一方合谋，也就是说云服务器只负责提供额外的计算能力或者依照协议指令传送特定内容.

现在我们分别定义发送方安全和接收方安全.

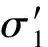
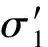
3) 针对接收方的发送方安全定义.对于接收方的任意选择集合C={σ1,σ2,…,σk}，发送方对接收方并未选择地输入值的加密结果应与随机计算不可区分.

3 单服务器辅助的n取k茫然传输协议

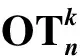
在本节中，我们给出一个半诚实敌手模型下的单服务器辅助的n取k茫然传输协议的具体过程.

协议所设计的系统模型如图1所示.协议共涉及3个参与方:发送方S、接收方R和云服务器Server.协议一共需要进行3轮交互.首先，R根据自己的选择构造出多项式，并将多项式的系数分割成2部分分别发送给S和Server；接着，S接收到的部分系数后计算RAND函数的部分结果，并将自己的输入嵌入到其中；最后，Server接收到来自S和R的消息后完成RAND函数的全部运算，将函数值发送给R，R在本地进行解密获得自己所选的值.

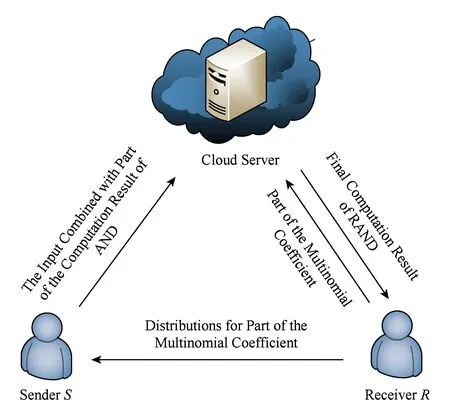
Fig. 1 The system model图1 系统模型

协议.单服务器辅助的高效n取k茫然传输协议.

输入：S输入n个值(x1,x2,…,xn)∈{0,1}n、R输入k个值(σ1,σ2,…,σk)∈{1,2,…,n}、云服务器Server没有输入；

辅助输入：安全参数n以及一个q阶群G，其生成元为g0；

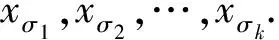
协议执行过程：

步骤1.R随机选择一个k阶多项式f(x)=(x-σ1)(x-σ2)…(x-σk)+β=a0+a1x+…+ak-1xk-1+xkmodq，其中β∈q.针对任意i=0,1,…,k-1，R计算并将(c0,c1)发送给S，将(c2,c3,…,ck-1)发送给云服务器Server.然后，R随机选择y1,y2,…,yn∈q，并将这n个值分别发送给S和Server.此外，R随机选择一个σm∈{σ1,σ2,…,σk}以及r∈q，并计算和h=gβ，然后将(g,h)发送给Server.

步骤4.R输出：

1) 针对步骤1中R随机选择的σm，R计算：

2) 针对每一个σj∈{σ1,σ2,…,σk}且σj∉σm，R计算：

3.2协议正确性分析

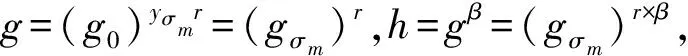
1) 针对i=σm，有f(i)=β，

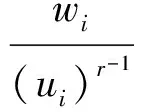
2) 针对每一个i∈{σ1,σ2,…,σk}但i≠σm,同样有f(i)=β，计算得到：

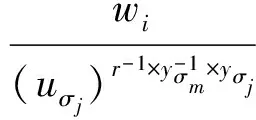
3) 当i∈{1,2,…,n}但i∉{σ1,σ2,…,σk}，此时f(i)≠β，则计算为

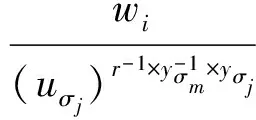
综上可以看出，接收方R能且仅能获得与自己选择相对应的k个值.

3.3协议安全性证明

下面我们给出协议的形式化安全证明.

定理1. 如果云服务器Server是诚实但好奇的且与发送方S相互独立，那么针对发送方协议满足接收方的安全性要求.

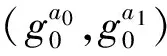
证毕.

定理2. 如果在群G上DDH假设成立，并且发送方S与云服务器Server是诚实但好奇的且相互独立，那么针对云服务器协议满足接收方的安全性要求.

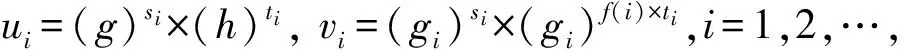
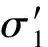
证毕.

定理3. 如果在群G上DDH假设成立，并且发送方S与云服务器Server是诚实但好奇的且相互独立，那么针对接收方协议满足发送方的安全性要求.

证明. 首先我们分析接收方R通过恶意行为来获取除自己选择外的值.接收方R可以试图构造一个多项式f(x)满足f(1)=f(2)=…=f(n)=β，从而可以恢复出发送方S的n个输入.这必然导致所构造出的多项式的阶大于k，在协议中云服务器Server检查了接收方R所发送的系数的个数，利用这个方法可以将多项式f(x)的阶严格限制为k，因此n个元组中DH元组的个数也是k.接下来证明接收方R不可能从n-k个非DH元组中获取额外信息.

根据RAND函数的性质，如果(w,x,y,z)为非DH元组，那么RAND(w,x,y,z)的结果是群G中的随机值.假设接收方的输入为(σ1,σ2,…,σk)，对于每一个j∉{σ1,σ2,…,σk}对应的(gj,g,hj,h)都不是DH元组.不妨从q中随机选择a和b，使得hj=(gj)a，h=gb,且a≠b.为了证明RAND(gj,g,hj,h)的结果在群G中是随机的，只需说明这里α,β随机取自q.由于RAND(gj,g,hj,h)=((gj)s×(hj)t,(g)s×(h)t)，这里s,t随机取自q，因此上述的概率是来自于s和t的随机性.令g=(gj)γ，γ随机取自q，那么元组(gj,g,hj,h)可以表示为(gj,(gj)γ,(gj)a,(gj)γ×b)，相应的RAND(gj,g,hj,h)=((gj)s+a×t,(gj)s×γ+γ×b×t).这样，对于方程组：

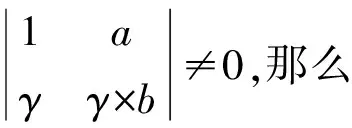
综上所述，我们完成对协议的安全性证明.

证毕.

3.4协议效率分析与比较

我们设计的协议中需要交互3轮:第1轮接收方R向同时向发送方S和云服务器Server发送消息；第2轮发送方S向云服务器Server发送一系列本地计算的结果；第3轮云服务器Server接收到发送方S发送的消息后将四元组“加密”后发送给接收方R，R在本地进行解密运算.

每一轮中具体的指数运算如下：

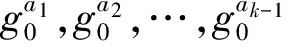
2) 发送方S共进行了4n-1次群指数运算.2n次群指数运算用来计算矩阵：

n-1次群指数运算用来计算矩阵：

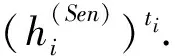
3) 云服务器Server共进行2(k+1)n+1-k次群指数运算.(k-1)n次用于计算矩阵：

(n-1)(k-1)次用于计算矩阵：

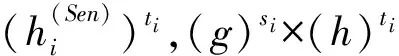
最后，我们统计出协议中的各参与方发送的群元素的个数：

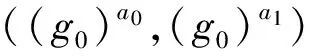
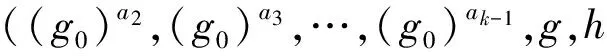
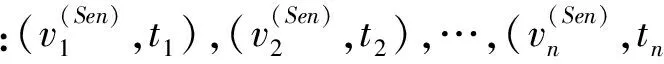
3) 云服务器Sever把2n个元素发送给接收方R：(u1,w1),(u2,w2),…,(un,wn).

表1是我们所设计的协议与文献[12,45]的对比结果.Chu等人[19]提出的n取k茫然传输协议不需要云服务器辅助，因此需要发送方和接收方进行大量群指数运算.Wei等人提出的协议将大部分群指数运算外包至2个云服务器，从而降低发送方和接收方的群指数运算.我们的协议仅使用一个云服务器且相对高效.

Table 1 Comparison of k-out-of-n Oblivious Transfer Protocols

4 结束语

[1] Li Zhenhua, Dai Yafei, Chen Guihai, et al. Content Distribution for Mobile Internet: A Cloud-based Approach[M]. Singapore: Springer Science Business Media, 2016

[2] Liu Zhe, Weng Jian, Hu Zhi, et al. Efficient elliptic curve cryptography for embedded devices[J]. ACM Trans on Embedded Computing Systems, 2016, 16(2): Article No 53

[3] Liu Zhe, Seo H, Großschädl J, et al. Efficient imple-mentation of NIST-compliant elliptic curve cryptography for 8-bit AVR-based sensor nodes[J]. IEEE Trans on Information Forensics and Security, 2016, 11(7): 1385-1397

[4] Jiang Han, Xu Qiuliang. Advances in key techniques of practical secure multi-party computation[J]. Journal of Computer Research and Development, 2015, 52(10): 2247-2257 (in Chinese)

(蒋瀚, 徐秋亮. 实用安全多方计算协议关键技术研究进展[J]. 计算机研究与发展, 2015, 52(10): 2247-2257)

[5] Rabin M O. How to exchange secrets with oblivious transfer, TR-81[R]. Cambridge, MA: Harvard University, 1981

[6] Even S, Goldreich O, Lempel A. A randomized protocol for signing contracts[J]. Communications of the ACM, 1985, 28(6): 637-647

[7] Brassard G, Crepeau C, Robert J M. All-or-nothing disclosure of secrets[G] //LNCS 263: Advances in Cryptology (CRYPTO 1986). Berlin: Springer, 1986: 234-238

[8] Stern J P. A new and efficient all-or-nothing disclosure of secrets protocol[G] //LNCS 1514: Advances in Cryptology (Asiacrypt 1998). Berlin: Springer, 1998: 357-371

[9] Cramer R, Shoup V. Universal Hash proofs and a paradigm for adaptive chosen ciphertext secure public-key encryption[G] //LNCS 2332: Advances in Cryptology (EUROCRYPT 2002). Berlin: Springer, 2002: 45-64

[10] Kalai Y T. Smooth projective hashing and two-message oblivious transfer[G] //LNCS 3494: Advances in Cryptology (EUROCRYPT 2005). Berlin: Springer, 2005: 78-95

[11] Naor M, Pinkas B. Efficient oblivious transfer protocols[C]//Proc of the 12th Annual ACM-SIAM Symp on Discrete Algorithms (SODA). New York: ACM, 2001: 448-457.

[12] Tzeng W G. Efficient 1-out-noblivious transfer schemes[G] //LNCS 2274: Public Key Cryptography. Berlin: Springer, 2002: 159-171

[13] Wei Xiaochao, Jiang Han, Zhao Chuan. An efficient 1-out-of-noblivious transfer protocol with full simulation[J]. Journal of Computer Research and Development, 2016, 53(11): 2475-2481 (in Chinese)

(魏晓超, 蒋瀚, 赵川. 一个高效可完全模拟的n取1茫然传输协议[J]. 计算机研究与发展, 2016, 53(11): 2475-2481)

[14] Lindell A Y. Efficient fully-simulatable oblivious transfer[G] //LNCS 4964: Topics in Cryptology (CT-RSA 2008). Berlin: Springer, 2008: 52-70

[15] Peikert C, Vaikuntanathan V, Waters B. A framework for efficient and composable oblivious transfer[G] //LNCS 5157: Advances in Cryptology (CRYPTO 2008). Berlin: Springer, 2008: 554-571

[16] Feng Tao, Ma Jianfeng, Li Fenghua. Efficient and universally composable security oblivious transfer[J]. Acta Electronica Sinica, 2008, 36(1): 17-23 (in Chinese)

(冯涛, 马建峰, 李凤华. UC安全的高效不经意传输协议[J]. 电子学报, 2008, 36(1): 17-23)

[17] Green M, Hohenberger S. Universally composable adaptive oblivious transfer[G] //LNCS 5350: Advances in Cryptolog (Asiacrypt 2008). Berlin: Springer, 2008: 179-197

[18] Garay J A, Ishai Y, Kumaresan R, et al. On the complexity of UC commitments[G] //LNCS 8441: Advances in Cryptology (CRYPTO 2014). Berlin: Springer, 2014: 677-694

[19] Chu C K, Tzeng W G. Efficientk-out-of-noblivious transfer schemes with adaptive and non-adaptive queries[G] //LNCS 3386: Public Key Cryptography (PKC 2005). Berlin: Springer, 2005: 172-183

[20] Zhang Jianhong, Wang Yumin. Two provably securek-out-of-noblivious transfer schemes[J]. Applied Mathematics and Computation, 2005, 169(2): 1211-1220

[21] Camenisch J, Neven G, Shelat A. Simulatable adaptive oblivious transfer[G] //LNCS 4515: Advances in Cryptology (EUROCRYPT 2007). Berlin: Springer, 2007: 573-590

[22] Zeng Bin, Tartary C, Xu Peng, et al. A practical framework fort-out-of-noblivious transfer with security against covert adversaries[J]. IEEE Trans on Information Forensics and Security, 2012, 7(2): 465-479

[23] Harnik D, Ishai Y, Kushilevitz E, et al. OT-combiners via secure computation[G] //LNCS 4948: Theory of Cryptography. Berlin: Springer, 2008: 393-411

[24] Nielsen J B, Nordholt P S, Orlandi C, et al. A new approach to practical active-secure two-party computation[G]//LNCS 7417: Advances in Cryptology (CRYPTO 2012). Berlin: Springer, 2012: 681-700

[25] Asharov G, Lindell Y, Schneider T, et al. More efficient oblivious transfer extensions[J]. Journal of Cryptology, 2017, 30(3): 805-858

[26] Patra A, Sarkar P, Suresh A. Fast actively secure OT extension for short secrets[C] //Proc of the 24th Network and Distributed System Security Symp (NDSS). Reston, VA: Internet Society, 2017

[27] Zhao Chuan, Jiang Han, Wei Xiaochao, et al. Cut-and-choose bilateral oblivious transfer and its application[C] //Proc of the 14th IEEE Int Conf on Trust, Security and Privacy in Computing and Communications. Los Alamitos, CA: IEEE Computer Society, 2015: 384-391

[28] Wei Xiaochao, Jiang Han, Zhao Chuan, et al. Fast cut-and-choose bilateral oblivious transfer for malicious adversaries[C] //Proc of the 15th IEEE Int Conf on Trust, Security and Privacy in Computing and Communications. Los Alamitos, CA: IEEE Computer Society, 2016: 418-425

[29] Plesch M, Pawowski M, Pivoluska M. 1-out-of-2 oblivious transfer using a flawed bit-string quantum protocol[J]. Physical Review A, 2017, 95(4): 042324

[30] Yang Yugang, Yang Rui, Cao Weifeng, et al. Flexible quantum oblivious transfer[J]. International Journal of Theoretical Physics, 2017, 56(4): 1286-1297

[31] Van Dijk M, Clarke D, Gassend B, et al. Speeding up exponentiation using an untrusted computational resource[J]. Designs, Codes and Cryptography, 2006, 39(2): 253-273

[32] Ma Xu, Li Jin, Zhang Fangguo. Outsourcing computation of modular exponentiations in cloud computing[J]. Cluster Computing, 2013, 16(4): 787-796

[33] Hohenberger S, Lysyanskaya A. How to securely outsource cryptographic computations[G] //LNCS 3378: Theory of Cryptography Conference (TCC 2005). Berlin: Springer, 2005: 264-282

[34] Chen Xiaofeng, Li Jin, Ma Jianfeng, et al. New algorithms for secure outsourcing of modular exponentiations[J]. IEEE Trans on Parallel and Distributed Systems, 2014, 25(9): 2386-2396

[35] Wang Yujie, Wu Qianhong, Wong D S, et al. Securely outsourcing exponentiations with single untrusted program for cloud storage[G] //LNCS 8712: Computer Security (ESORICS 2014). Berlin: Springer, 2014: 326-343

[36] Chevalier C, Laguillaumie F, Vergnaud D. Privately outsourcing exponentiation to a single server: Cryptanalysis and optimal constructions[C] //LNCS 9878: Computer Security (ESORICS 2016). Berlin: Springer, 2016: 261-278

[37] Tsang P P, Chow S S M, Smith S W. Batch pairing delegation[G] //LNCS 4752: Advances in Information and Computer Security. Berlin: Springer, 2007: 74-90

[38] Canard S, Devigne J, Sanders O. Delegating a pairing can be both secure and efficient[G] //LNCS 8479: Applied Cryptography and Network Security. Berlin: Springer, 2014: 549-565

[39] Xu G, Amariucai G T, Guan Y. Delegation of computation with verification outsourcing: Curious verifiers[J]. IEEE Trans on Parallel and Distributed Systems, 2017, 28(3): 717-730

[40] Gennaro R, Gentry C, Parno B. Non-interactive verifiable computing: Outsourcing computation to untrusted workers[G] //LNCS 6223: Advances in Cryptology (CRYPTO 2010). Berlin: Springer, 2010: 465-482

[41] Carter H, Mood B, Traynor P, et al. Secure outsourced garbled circuit evaluation for mobile devices[J]. Journal of Computer Security, 2016, 24(2): 137-180

[42] Carter H, Lever C, Traynor P. Whitewash: Outsourcing garbled circuit generation for mobile devices[C] //Proc of the 30th Annual Computer Security Applications Conf. New York: ACM, 2014: 266-275

[43] Mohassel P, Orobets O, Riva B. Efficient server-aided 2PC for mobile phones[J]. Proceedings on Privacy Enhancing Technologies, 2016, 2016(2): 82-99

[44] Carter H, Mood B, Traynor P, et al. Outsourcing secure two-party computation as a black box[J]. Security and Communication Networks, 2016, 9(14): 2261-2275

[45] Wei Xiaochao, Zhao Chuan, Jiang Han, et al. Practical server-aidedk-out-of-noblivious transfer protocol[G] //LNCS 9663: Green, Pervasive, and Cloud Computing 2016. Berlin: Springer, 2016: 261-277

[46] Kamara S, Mohassel P, Raykova M. Outsourcing multi-party computation[OL]. [2017-08-25]. https://eprint.iacr.org/2011/272/pdf

AnEfficientSingleServer-Aidedk-out-of-nObliviousTransferProtocol

Zhao Shengnan1, Jiang Han1, Wei Xiaochao2, Ke Junming1, and Zhao Minghao1

1(SchoolofComputerScienceandTechnology,ShandongUniversity,Jinan250101)2(SchoolofInformationScienceandEngineering,ShandongNormalUniversity,Jinan250358)

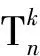
oblivious transfer (OT); outsourcing computing; decisional Diffie-Hellamn (DDH) assumption; semi-honest model; secure multi-party computation

TP301

ZhaoShengnan, born in 1994. PhD candidate. His main research interests include secure multiparty computation and search on encrypted data.

JiangHan, born in 1974. PhD and lecturer. His main research interests include theory of cryptography, side-channel attacks and cryptographic protocols.

WeiXiaochao, born in 1990. PhD and lecturer. His main research interests include secure multiparty computation and search on encrypted data (weixiaochao2008@163.com).

KeJunming, born in 1994. Master candidate. His main research interests include computer security and cryptocurrencies (Junmingke1994@gmail.com).

ZhaoMinghao, born in 1991. PhD candidate in Tsinghua University. Received his MSc degree in Shandong University and bachelor degree in Harbin Engineering University. Student member of ACM, CCF and CACR. His main research interests include cloud computing, storage system, mobile computing, privacy-preserving techniques and applied cryptography.