基于随机波动率模型的可转换债券定价研究

汤芮 安徽财经大学金融学院金融工程专业

基于随机波动率模型的可转换债券定价研究

汤芮 安徽财经大学金融学院金融工程专业

如何对可转换债券进行合理的定价是当今数理金融学研究的重要课题之一。然而纵观现存的大量研究几乎都是在假设波动率为常数的前提下，将可转债分成债券与期权两个相互独立的部分进行定价求解。而实际中波动率往往是随机的，将波动率的随机性考虑到定价之中具有更大的实际意义。本项目将通过建立波动率为随机条件下的期权定价模型从而对可转换债券进行更精确地定价研究。

可转换债券 随机波动率 heston模型

一、引言

可转换债券是指允许持有者在规定的时间内将债券按照一定的转股比率换成公司股份的一种债券。从本质上说，就是在公司债券的基础上附加一份期权。但不论是相比于基础金融资产股票、债券，还是衍生金融产品期货、期权等，可转换债券都更具优势。从国际市场上看，可转债已成为多数发达国家金融资产的重要组成部分。因此如何对可转换债券进行合理的定价具有很强的学术价值和理论意义。

关于可转换债券的定价研究最早始于20世纪70年代，Black和Scholes（1973）在政治经济杂志上发表了著名的B-S期权定价模型，为可转换债券的定价提供了一定的理论基础。Ingersoll（1977）率先提出基于公司价值的可转债定价模型，并且得到了模型的解析解。同年Brennan和Schwartz在此基础上，进一步考虑了发行公司的最优赎回政策，使用有限差分法得到了可转债的价格。Sirbu（2006）基于公司价值模型，将可转债价格看成是股东权益与债务价值的双人博弈，从而简化为最优停时问题进行定价。Laura Ballotta和Loannis Kyriakou（2014）假设公司价值服从指数-跳扩散过程，对利率随机波动条件下的可转换债券进行了数值定价。

由于这些模型均是在基于公司价值的基础上给出的，而公司价值相对来说刻画难度比较大，因此McConnell和Schwartz（1986）最早提出了基于公司股票价值的可转换债券定价模型。在此基础上，K.Tsiveriotis和C.Fernandes（1998）两位学者将可转换债券分为股权和债权两个部分，进一步给出了基于股票价格的单因素模型。Kovalov和Linetsky（2008），考虑了利率，股票价格，波动率和违约风险四个因素，提出了可转债定价的多因素模型，并通过建立偏微分方程，利用有限元方法进行求解。Stuart McCrary（2015）在John Hull（2010）二叉树模型的基础上，考虑了违约风险和随机波动率，提出了期权定价的三叉树模型。

在我国，可转换债券的研究起步较晚。李莉等（2009）考虑了利率期限结构和信用风险对可转债价值的影响，利用二叉树和蒙特卡罗模拟方法建立了双因素定价模型。同年，闻岳春和邱小平认为由于我国存在转股向下修正预案，可转换债权的价格较大程度被低估，因此在考虑了修正预期的前提下，采用蒙特卡罗模拟法对可转债进行了定价。张为国等（2010）为考虑股票波动和无风险利率等不确定因素影响，假设连续复利率、无风险利率、股票价格和股价波动率等均为模糊数，运用模糊集理论，得出了可转债的模糊定价模型。李念夷和陈懿冰（2011）则考虑了可转债的违约风险，以相似经营业绩和同等风险的企业债券收益率而不是无风险利率作为贴现率，给出了基于违约风险的三叉树定价模型。贾兆丽等（2015）假设公司资产服从马氏股价过程，同时利用快速傅里叶变换方法，给出了马氏骨架过程下可转债的定价公式。可以看出，国内有关可转换债券的研究大多是在国外已有模型的基础上进行的，缺乏一定的独创性和突破性。

二、模型构建

纵观目前国内外学者对于可转换债券的研究，基本可以将定价模型大致分为两类:一是通过对影响可转换债券定价模型的一系列因素包括利率、股票价格等进行分析或模拟，从而确定可转换债券的价格；二是将可转换债券分解成独立的债券和期权，分别对两部分定价后再进行加总得到可转换债券的价格。通过总结我们发现第二种方法普遍被业界接受认同，因此本文也将从可转换债券的债券和期权两个部分着手，研究可转债的定价。

可转换债权中纯债券部分价值即为未来利息与最后本金和现金流的贴现值，而对于内嵌期权部分，大部分学者都是在假设标的资产波动率为常数，可转换债权的价格只受标的资产价格变动影响的前提下，利用Black-Scholes公式进行建模求解。然而在实际中，由于标的资产本身价格是随机波动的，所以波动率也应为随机变量。为使理论定价结果更贴近现实，本文将考虑在标的资产波动率为随机条件时期权的定价模型。

目前国内外关于随机波动率的研究已经比较深入，大致可分为离散时间的随机波动率和连续时间的随机波动率模型两类。在资产定价的研究中，连续型随机波动率模型使用频率相对更高。其中市场上的比较经典的随机波动率模型基本可以归纳为Hull-White模型、Stein-Stein模型和Heston模型三种。Hull-White 模型中假设标的资产价格服从扩散过程，波动率服从正扩散过程，虽然适应性较好，但只能得到定价公式的近似解而存在一定的难度和缺陷性；Stein-Stein模型中假设标的资产波动率服从OU，即均值回归过程，但由于模型中假设标的资产波动率可能存在负值，因此具有一定的局限性；而在仿射Heston模型中假设标的资产的波动率满足CIR模型，能很好诠释“波动率微笑”现象，同时给出定价模型具体的解析解，因而本文将在Heston模型的基础上，建立随机波动率下的定价模型。

具体地，本文将采取把可转换债券分解成独立的债券和期权两部分进行定价的方法，因此下文将主要从纯债券部分和纯期权两部分分别展开。

（一）纯债券部分价值模型

对于可转换债券中的纯债券部分，根据现金流贴现理论，可转换债券中债券部分的价值即为未来利息与最后本金和的现金流的贴现值。因此纯债券部分价值为：

其中B表示纯债券部分的价值；I表示每年收到的利息；r表示市场贴现率，一般指无风险利率；A表示债券本金；n表示从现在至到期日的剩余年限。

（二）纯期权部分价值模型

根据1993年Heston提出的模型，假设标的资产价格和波动率满足以下的随机微分方程组：

其中St表示标的资产价格，vt表示标的资产价格的方差，ws、wV为标准布朗运动且相关系数为ρ，k为均值回归系数，θ为长期方差，η为波动率方差，rt为收益率，假设为常数。

在Heston模型中期权价格满足偏微分方程：

同时Heston给出了方程的显形解，即欧式看涨期权的价格公式为：

（三）可转换债券的价格

综上所述，将纯债券部分价值和纯期权部分价值进行组合，得到可转换债券的定价公式为：

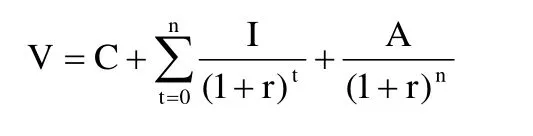
三、实证研究

本文选取了近十年国内的200多只可转换债券，根据信用评级、发行规模、上市起始和截止日等特征，以中行转债为代表进行实证分析。基本信息如下表所示。

债券名称 票面价值 信用评级 债券期限 票面利率 转股期限中行转债 100 AAA 2010.6.2-2016.6.2依次为0.5%、0.8%、1.1%、1.4%、1.7%、2%2010.12.2-2016.6.2

（一）纯债券部分价值

根据郑振龙和林海（2004）的研究表明，在中国特殊的制度背景下，可转债中股性占了绝大部分，而且中国的信用风险溢筹不高，因此使用无风险利率进行贴现并不会产生太大的影响。本文将一年期的SHIBOR利率（4.43%）作为作为无风险利率进行贴现。由（1）式可分别求出三种可转换的债券纯债券部分的价值。

以中行转债为例：面值为100元，存续期限为6年，票面利率从第一年的0.5%开始，逐年递增0.3%。不考虑债券的赎回和回售条款，得到中行转债的纯债券部分价值为：

（二）纯期权部分价值

1.运用Heston模型

（1）根据Heston模型的定价公式，在给定参数初始值的情况下，使用模拟退火法对模型进行参数校准。1993年Heston根据模型中五个参数的性质，给出了参数的限制范围。根据Heston给出的参数的范围，并结合等其他学者的研究结果，我们选取的参数的范围如下表所示：

参数 参数范围均值回归速度：k （0，20）

长期方差：θ （0，2）波动率方差：η （0，2）股价和波动率随机过程的相关系数：ρ（-1，1）初始方差：ν（0，2）

根据Gauthier & Rivaille(2009)确定初值的方法，本文设置待校准参数的初值为E={9.0，0.05，0.40，-0.5，0.04}。

（2）以中行转债为例，其转债条款中规定，初始转股价格为每股4.02元，即X=4.02；在中行转债发行时，中国银行股价为每股4.2元，即S=4.2；转债期限T-t=6(年)。因此根据Heston公式，得到欧式看涨期权的价格C=30.8657（元）

2.运用B-S模型

（1）历史波动率的计算首先根据可转债期限内标的资产价格的历史数据中估计，得到历史波动率。以中行转债为例，从2010年12月2日到2016年6月2日，共有1334个数据，第i日股票价格的连续复利收益率为，则基于收益率样本的标准差即为对应的日化历史波动率，其中。

（2）看涨期权价格的计算

根据B-S期权定价公式，可得到欧式看涨期权价格为

以中行转债为例，其转债条款中规定，初始转股价格为每股4.02元，即X=4.02；在中行转债发行时，中国银行股价为每股4.2元，即S=4.2；转债期限T-t=6(年)。因此

查询正态分布表可得：N(d1)=0.7895，N(d2)=0.5666，所以c=1.5698（元）。

由于转股价格为每股4.02元，每张可转换债券的面值为100元，所包含的期权价值C=100/4.02*1.5698=39.0498（元）

（三）可转换债券的价值

综上所述，以Heston模型计算出中行转债的价值V=C+B=30.8657+83.37=114.2357（元）；以B-S模型计算出的价值V=C+B=39.0498+83.37=122.4198（元）。均高于可转债的面值100元，但Heston模型计算出来的更贴合实际，计算效率更高。

四、结论

可转换债券在我国仍属于新兴金融衍生产品，考虑随机波动率下可转换债券的定价不论是在科研还是实务界都有着其重要的意义。本文将可转换债券的价值分成纯债券部分的价值和纯欧式看涨期权的价值，以中行转债为例，通过Heston岁随机波动率模型和B-S期权定价公式，分别计算出了可转换债券的理论价格。同时我们发现，不论是Heston还是B-S公式，计算出的理论价格均高于实际可转换债券的面值，但利用Heston模型计算出的价格更贴合实际。

了解可转债的定价机制，有助于融资者制订更加合理的可转债条款，成功发行可转债，同时也让投资者能更好地进行资金的分配和投资，进一步推动我国证券市场的发展。

安徽财经大学国家级大学生创新训练项目(项目编号:201610378447)。